2.1: Gráfica y pendiente
- Page ID
- 117416
A menudo, para hacernos una idea del comportamiento de una ecuación, haremos una imagen que represente las soluciones a las ecuaciones llamadas gráfica. Tengamos una introducción a la gráfica para que posteriormente podamos construir gráficas.
Un gráfico representa una visualización de las soluciones a una ecuación.
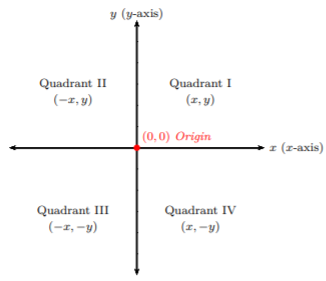
- El plano de coordenadas se divide en cuatro cuadrantes por una línea numérica horizontal, llamada\(x\) eje -y una línea numérica real vertical, llamada\(y\) eje.
- Los dos ejes se encuentran en el origen, donde\(x = 0\) y\(y = 0\).
- La coordenada x es la distancia horizontal desde el origen y la coordenada y es la distancia vertical desde el origen.
- Un par ordenado es donde se ubica un punto en el plano de coordenadas y se denota por\((x, y)\).
- Los cuadrantes se etiquetan en sentido antihorario comenzando en la parte superior derecha.
Las ubicaciones en el globo son similares a los pares ordenados. Cada número está a una distancia de un punto central, el origen, ubicado donde se encuentran el meridiano principal y el ecuador. Este “origen” se encuentra justo frente a la costa occidental de África.
Puntos y líneas
Trazar cada par ordenado e identificar el cuadrante en el que se encuentra el par ordenado:\[A(−1, −5),\: B(3, −1),\: C(−2, 3),\: D(4, 2),\: E(0, 4),\: F(3, 0)\nonumber\]
Solución
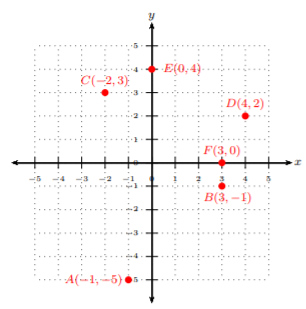
- Para el punto\(A(−1, −5)\), observe que la\(x\) coordenada -es\(−1\). Dado que la\(x\) coordenada -es la distancia horizontal desde el origen, entonces movemos la\(1\) unidad hacia la izquierda. Mirando la\(y\) coordenada\(−5\) -, vemos que esta será la distancia vertical. De ahí que moveremos\(5\) las unidades hacia abajo desde el origen. Comenzando por el origen, mueva una unidad a la izquierda, luego\(5\) unidades hacia abajo. \(A\)El punto está en el cuadrante III.
- Para el punto\(B(3, −1)\), observe que la\(x\) coordenada -es\(3\). Dado que la\(x\) coordenada -es la distancia horizontal desde el origen, entonces movemos\(3\) las unidades hacia la derecha. Mirando la\(y\) coordenada\(−1\) -, vemos que esta será la distancia vertical. De ahí que moveremos una unidad hacia abajo desde el origen. Comenzando por el origen, mueva\(3\) las unidades a la derecha, luego\(1\) la unidad hacia abajo. \(B\)El punto está en el cuadrante IV.
- Para el punto\(C(−2, 3)\), observe que la\(x\) coordenada -es\(−2\). Dado que la\(x\) coordenada -es la distancia horizontal desde el origen, entonces movemos\(2\) las unidades hacia la izquierda. Mirando la\(y\) coordenada\(3\) -, vemos que esta será la distancia vertical. De ahí que moveremos\(3\) unidades hacia arriba desde el origen. Comenzando por el origen, mover\(2\) unidades a la izquierda, luego\(3\) unidades hacia arriba. \(C\)El punto está en el cuadrante III.
- Para el punto\(D(4, 2)\), observe que la\(x\) coordenada -es\(4\). Dado que la\(x\) coordenada -es la distancia horizontal desde el origen, entonces movemos\(4\) las unidades hacia la derecha. Mirando la\(y\) coordenada\(2\) -, vemos que esta será la distancia vertical. De ahí que moveremos\(2\) unidades hacia arriba desde el origen. Comenzando por el origen, mueva\(4\) las unidades a la derecha, luego\(2\) las unidades hacia arriba. \(D\)El punto está en el cuadrante I.
- Para el punto\(E(0, 4)\), observe que la\(x\) coordenada -es\(0\). Dado que la\(x\) coordenada -es la distancia horizontal desde el origen, entonces no movemos ninguna unidad horizontalmente desde el origen. Mirando la\(y\) coordenada\(4\) -, vemos que esta será la distancia vertical. De ahí que moveremos\(4\) unidades hacia arriba desde el origen. Comenzando por el origen, mover\(4\) las unidades hacia arriba. \(E\)El punto no está en ningún cuadrante ya que se encuentra en el\(y\) eje -eje.
- Para el punto\(F(3, 0)\), observe que la\(x\) coordenada -es\(3\). Dado que la\(x\) coordenada -es la distancia horizontal desde el origen, entonces movemos\(3\) las unidades hacia la derecha. Mirando la\(y\) coordenada\(0\) -, vemos que esta será la distancia vertical. De ahí que no moveremos ninguna unidad verticalmente desde el origen. Comenzando por el origen, mueva\(3\) las unidades a la derecha. \(F\)El punto no está en ningún cuadrante ya que se encuentra en el\(x\) eje -eje.
Observe, en puntos\(A,\: B,\: C,\) las coordenadas negativas no implicaban distancia negativa del origen. El negativo en estas coordenadas implica la dirección en la que nos movemos: horizontal- nos movemos hacia la izquierda o hacia la derecha, vertical- nos movemos hacia arriba o hacia abajo. Si la\(x\) coordenada -es negativa, entonces nos movemos hacia la izquierda. Si la\(y\) coordenada -es negativa, entonces nos movemos hacia abajo.
De Ejemplo\(\PageIndex{1}\), con puntos\(E\) y\(F\), pudimos ver que estos puntos no yacían en un cuadrante, sino sobre un eje. Estos son puntos especiales en las gráficas y se denominan intercepciones.
- La intercepción x de una gráfica es el punto (s) donde la gráfica cruza el\(x\) eje -eje, es decir,\(y = 0\).
- La intercepción y de una gráfica es el punto (s) donde la gráfica cruza el\(y\) eje -eje, es decir,\(x = 0\).
Gráfica\(y = 1 − x\) trazando las intercepciones.
Solución
Para encontrar las\(y\) intercepciones\(x\) y, podemos seguir la definición anterior y encontrar dónde\(y = 0\) y\(x = 0\), respectivamente. Hagamos una mesa.
Mesa\(\PageIndex{1}\)
| \(x\) | \(y=1-x\) | \((x,y)\) |
|---|---|---|
| \ (x\) ">\(\color{blue}{0}\color{black}{}=1-x\Longrightarrow x=\color{red}{1}\) | \ (y=1-x\) ">\(0\) | \ ((x, y)\) ">\((\color{red}{1}\color{black}{},0)\) |
| \ (x\) ">\(0\) | \ (y=1-x\) ">\(y=1-\color{blue}{0}\color{black}{}=\color{red}{1}\) | \ ((x, y)\) ">\((0,\color{red}{1}\color{black}{})\) |
Podemos ver cuando\(y = 0,\: x = 1\) desde\(0 = 1 − x\) solo cuando\(x = 1\). Trazar las dos intercepciones desde la mesa. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Dibuja la línea para llenar la cuadrícula y poner flechas en los extremos. Se recomienda comprar una regla pequeña de 6 pulgadas para hacer lindas líneas rectas.
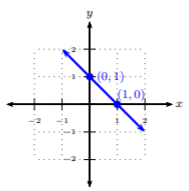
El propósito principal de las gráficas no es trazar puntos aleatorios, sino dar una imagen de las soluciones a una ecuación. Podemos tener una ecuación como\(y = 2x − 3\) y estar interesados en el tipo de soluciones que son posibles para esta ecuación. Podemos visualizar la solución haciendo una gráfica de posibles\(x\) y\(y\) combinaciones que hacen de esta ecuación una afirmación verdadera. Tenemos que empezar por encontrar posibles\(x\) y\(y\) combinaciones. Esto lo hacemos usando una tabla de valores.
Gráfica\(y = 2x − 3\) trazando puntos, es decir, haciendo una tabla en T.
Solución
Por lo general, elegimos tres\(x\) coordenadas y encontramos\(y\) los valores correspondientes. Cada\(x\) valor es positivo, negativo y cero. Esta es una práctica común, pero no requerida.
Mesa\(\PageIndex{2}\)
| \(x\) | \(y=2x-3\) | \((x,y)\) |
|---|---|---|
| \ (x\) ">\(-1\) | \ (y=2x-3\) ">\(y=2(\color{blue}{-1}\color{black}{})-3=-2-3=-5\) | \ ((x, y)\) ">\((-1,-5)\) |
| \ (x\) ">\(0\) | \ (y=2x-3\) ">\(y=2(\color{blue}{0}\color{black}{})-3=0-3=-3\) | \ ((x, y)\) ">\((0,-3)\) |
| \ (x\) ">\(1\) | \ (y=2x-3\) ">\(y=2(\color{blue}{1}\color{black}{})-3=2-3=-1\) | \ ((x, y)\) ">\((1,-1)\) |
Trazar los tres pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Dibuja la línea para llenar la cuadrícula y poner flechas en los extremos. Se recomienda comprar una regla pequeña de 6 pulgadas para hacer lindas líneas rectas.
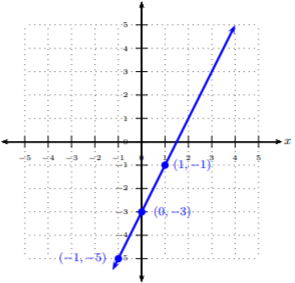
Gráfica\(2x − 3y = 6\) trazando puntos, es decir, haciendo una tabla en T.
Solución
Empecemos por elegir\(x\) -valores para la tabla. Observe que esta ecuación no es tan simple como el ejemplo anterior, así que tendremos que hacer un poco de álgebra para resolver el\(y\) valor -value. Después, rellena la tabla.
Mesa\(\PageIndex{3}\)
| \(x\) | \(y\) | \((x,y)\) |
|---|---|---|
| \ (x\) ">\(-3\) | \ (y\) "> | \ ((x, y)\) "> |
| \ (x\) ">\(0\) | \ (y\) "> | \ ((x, y)\) "> |
| \ (x\) ">\(3\) | \ (y\) "> | \ ((x, y)\) "> |
Evaluemos\(2x − 3y = 6\) para cada uno de los\(x\) -valores elegidos:
\(x=-3:\)\[\begin{aligned}2(-3)-3y&=6 \\ -6-3y+\color{blue}{6}\color{black}{}&=6+\color{blue}{6}\color{black}{} \\ \color{blue}{-\frac{1}{3}}\color{black}{}\cdot -3y&=12\cdot\color{blue}{-\frac{1}{3}}\color{black}{} \\ y&=-4\end{aligned}\]
\(x=0\):\[\begin{aligned}2(0)-3y&=6 \\ 0-3y&=6 \\ \color{blue}{-\frac{1}{3}}\color{black}{}\cdot -3y&=6\cdot\color{blue}{-\frac{1}{3}}\color{black}{} \\ y&=-2\end{aligned}\]
\(x=3:\)\[\begin{aligned}2(3)-3y&=6 \\ 6-3y+\color{blue}{(-6)}\color{black}{}&=6+\color{blue}{(-6)}\color{black}{} \\ \color{blue}{-\frac{1}{3}}\color{black}{}\cdot -3y&=0\cdot\color{blue}{-\frac{1}{3}}\color{black}{} \\ y&=0\end{aligned}\]
Ahora, rellenamos la tabla con\(y\) -valores y pares ordenados, y luego graficamos\(2x − 3y = 6\).
Mesa\(\PageIndex{4}\)
| \(x\) | \(y\) | \((x,y)\) |
|---|---|---|
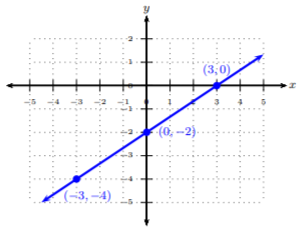
| \ (x\) ">\(-3\) | \ (y\) ">\(-4\) | \ ((x, y)\) ">\((-3,-4)\) |
| \ (x\) ">\(0\) | \ (y\) ">\(-2\) | \ ((x, y)\) ">\((0,-2)\) |
| \ (x\) ">\(3\) | \ (y\) ">\(0\) | \ ((x, y)\) ">\((3,0)\) |
Obtención de la Pendiente de una Línea a partir de su Gráfica
A medida que graficamos líneas, queremos identificar diferentes propiedades de líneas. Una de las propiedades más importantes de una línea es su pendiente.
La pendiente de una línea es la medida de la inclinación de la línea.
- Denotamos pendiente con\(m\). Una teoría de matemáticos que comenzaron a trabajar con pendiente fue que se le llamó la pendiente modular.
- A medida que\(|m|\) aumenta, la línea se vuelve más pronunciada. A\(|m|\) medida que disminuye, la línea se vuelve más plana.
- Una línea que sube de izquierda a derecha tiene una pendiente positiva y una línea que cae de izquierda a derecha tiene pendiente negativa.
- \(m\)es el cambio de\(y\) dividido por el cambio en\(x\), es decir,\[m=\frac{\Delta y}{\Delta x}=\frac{\text{Change in }y}{\text{Change in }x}=\frac{rise}{run}\nonumber\]
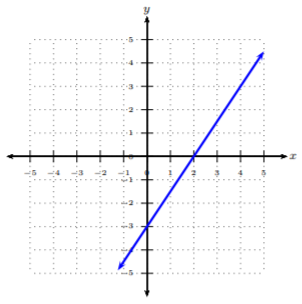
Encuentra la pendiente de la gráfica dada de la línea.
Solución
Comenzamos en un punto bien definido, preferiblemente un punto en el\(y\) eje -eje, es decir, la\(y\) -intercepción. Después, cuente el número de unidades que subimos (arriba/abajo) y corremos (izquierda/derecha) para llegar al siguiente punto bien definido. Empezaremos en\((0, −3)\) y llegaremos al siguiente punto,\((2, 0)\). Observe que elevamos\(3\) unidades ascendentes y corremos a las\(2\) unidades adecuadas. Usando la relación,\(m = \frac{rise}{run}\), obtenemos el ascenso para ser\(3\) y la carrera para ser\(2\):\[m=\frac{rise}{run}=\frac{3}{2}\nonumber\]
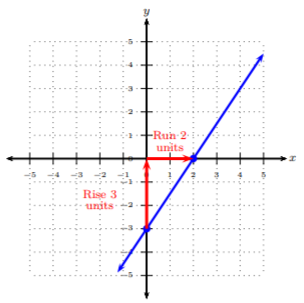
Así, la pendiente es\(\frac{3}{2}\).
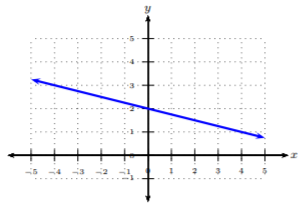
Encuentra la pendiente de la gráfica dada de la línea.
Solución
Comenzamos en un punto bien definido, preferiblemente un punto en el\(y\) eje -eje, es decir, la\(y\) -intercepción. Después, cuente el número de unidades que subimos (arriba/abajo) y corremos (izquierda/derecha) para llegar al siguiente punto bien definido. Empezaremos en\((0, 2)\) y llegaremos al siguiente punto,\((4, 1)\). Observe que subimos\(1\) unidades a la baja y corremos hacia\(4\) las unidades adecuadas. Usando la relación,\(m = \frac{rise}{run}\), obtenemos el ascenso para ser\(−1\) y la carrera para ser\(4\):\[m=\frac{rise}{run}=\frac{-1}{4}\nonumber\]
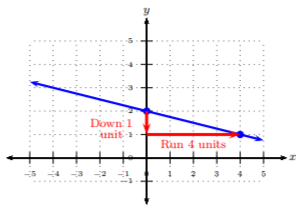
Así, la pendiente es\(-\frac{1}{4}\).
Mirando Ejemplos\(\PageIndex{5}\) y \(\PageIndex{6}\), fíjate en la pendiente. Ya que, en Ejemplo\(\PageIndex{5}\), la pendiente era\(\frac{3}{2}\), que es mayor que la pendiente en \(\PageIndex{6}\), Ejemplo\(\PageIndex{5}\) es una línea más pronunciada que Ejemplo\(\PageIndex{6}\). Además, el negativo en Ejemplo\(\PageIndex{6}\) representa la línea que cae de izquierda a derecha; de ahí la pendiente negativa.
Cuando los matemáticos franceses Rene Descartes y Pierre de Fermat desarrollaron por primera vez el plano de coordenadas y la idea de graficar líneas (y otras funciones), el\(y\) eje -eje no era una línea vertical.
Veamos dos casos especiales con líneas y su pendiente.
Encuentra la pendiente de la gráfica dada de la línea.
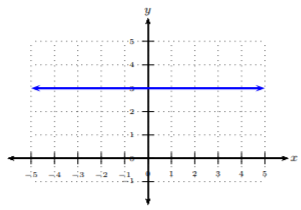
Solución
En esta gráfica, no hay subida, pero la carrera son\(3\) unidades. La pendiente es\(\frac{0}{3}= 0\). Cuando la pendiente de una línea es cero, entonces sabemos que la línea es una línea horizontal y viceversa.
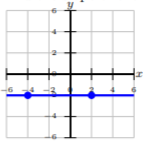
Encuentra la pendiente de la gráfica dada de la línea.
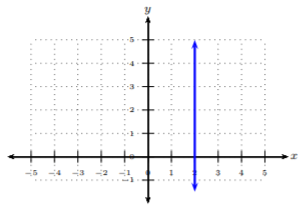
Solución
En esta gráfica, no hay corrida, pero la subida son\(2\) unidades. La pendiente es\(\frac{2}{0} =\) indefinida. Cuando la pendiente de una línea es indefinida, entonces sabemos que la línea es una línea vertical y viceversa.
Como puedes ver hay una gran diferencia entre tener una pendiente cero y tener pendiente indefinida. Recuerde, la pendiente es una medida de pendiente. La primera pendiente no es empinada en absoluto. De hecho, es plano. Por lo tanto, tiene una pendiente cero. La segunda pendiente no puede llegar a ser más pronunciada. Es tan empinada que no hay un número lo suficientemente grande como para expresar la pendiente. De ahí que sea una pendiente indefinida.
Obtención de la Pendiente de una Línea a partir de Dos Puntos
Podemos encontrar la pendiente de una línea a través de dos puntos sin ver los puntos en una gráfica. Podemos hacer esto usando una fórmula de pendiente. Si la subida es el cambio en\(y\) -valores, podemos calcularlo restando los\(y\) -valores de un punto. Del mismo modo, si run es un cambio en los\(x\) -valores, podemos calcularlo restando los\(x\) -valores de un punto.
Pendiente,\(m\), es el cambio de\(y\) dividido por el cambio en\(x\), es decir,\[m=\frac{\Delta y}{\Delta x}=\frac{\text{Change in }y}{\text{Change in }x}=\frac{rise}{run}=\frac{y_2-y_1}{x_2-x_1}=\frac{y_1-y_2}{x_1-x_2}\nonumber\]
Encuentra la pendiente entre los dos puntos\((−4, 3)\) y\((2, −9)\).
Solución
\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{Substitute in the ordered-pairs} \\ m=\frac{-9-3}{2-(-4)}&\text{Simplify} \\ m=\frac{-12}{6}&\text{Reduce} \\ m=-2&\text{Slope}\end{array}\nonumber\]
Ya que esta pendiente es\(−2\), entonces la gráfica de esta línea estaría cayendo de izquierda a derecha.
Encuentra la pendiente entre los dos puntos\((4, 6)\) y\((2, −1)\).
Solución
\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{Substitute in the ordered-pairs} \\ m=\frac{-1-6}{2-4}&\text{Simplify} \\ m=\frac{-7}{-2}&\text{Reduce, dividing by }-1 \\ m=\frac{7}{2}&\text{Slope}\end{array}\nonumber\]
Como esta pendiente es\(\frac{7}{2}\), entonces la gráfica de esta línea estaría subiendo de izquierda a derecha.
Encuentra la pendiente entre los dos puntos\((−4, −1)\) y\((−4, −5)\).
Solución
\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{Substitute in the ordered-pairs} \\ m=\frac{-5-(-1)}{-4-(-4)}&\text{Simplify} \\ m=\frac{-4}{0}&\text{Undefined} \\ m=\text{ undefined}&\text{Slope}\end{array}\nonumber\]
Dado que la pendiente es indefinida, entonces la gráfica de esta línea es una línea vertical.
Encuentra la pendiente entre los dos puntos\((3, 1)\) y\((−2, 1)\).
Solución
\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{Substitute in the ordered-pairs} \\ m=\frac{1-1}{-2-3}&\text{Simplify} \\ m=\frac{0}{-5}&\text{Reduce} \\ m=0&\text{Slope}\end{array}\nonumber\]
Dado que la pendiente es cero, entonces la gráfica de esta línea es una línea horizontal.
Encuentra el valor de\(y\) entre los puntos\((2, y)\) y\((5, −1)\) con pendiente\(−3\).
Solución
\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{We will plug values into slope formula} \\ -3=\frac{-1-y}{5-2}&\text{Simplify} \\ -3=\frac{-1-y}{3}&\text{Multiply both sides by }3 \\ \color{blue}{3}\color{black}{}\cdot -3=\frac{-1-y}{3}\cdot\color{blue}{3}\color{black}{}&\text{Simplify} \\ -9=-1-y&\text{Isolate the variable term} \\ -9+\color{blue}{1}\color{black}{}=-1-y+\color{blue}{1}\color{black}{}&\text{Simplify} \\ -8=-y&\text{Multiply each side by }-1 \\ \color{blue}{-1}\color{black}{}\cdot -8=-y\cdot \color{blue}{-1}\color{black}{} \\ 8=y&\text{Value of }y\end{array}\nonumber\]
Encuentra el valor de\(x\) tal que la pendiente entre los puntos\((−3, 2)\) y\((x, 6)\) es\(\frac{2}{5}\).
Solución
\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{We will plug values into slope formula} \\ \frac{2}{5}=\frac{6-2}{x-(-3)}&\text{Simplify} \\ \frac{2}{5}=\frac{4}{x+3}&\text{Multiply both sides by }x+3 \\ \color{blue}{(x+3)}\color{black}{}\cdot\frac{2}{5}=\frac{4}{x+3}\cdot\color{blue}{(x+3)}\color{black}{}&\text{Simplify} \\ \frac{2}{5}(x+3)=4&\text{Distribute} \\ \frac{2}{5}x+\frac{6}{5}=4&\text{Multiply by the LCD }=5 \\ \color{blue}{5}\color{black}{}\cdot\frac{2}{5}x+\color{blue}{5}\color{black}{}\cdot\frac{6}{5}=4\cdot\color{blue}{5}\color{black}{}&\text{Simplify} \\ 2x+6=20&\text{Isolate the variable term} \\ 2x+6+\color{blue}{(-6)}\color{black}{}=20+\color{blue}{(-6)}\color{black}{}&\text{Simplify} \\ 2x=14&\text{Multiply each side by the reciprocal of }2 \\ \color{blue}{\frac{1}{2}}\color{black}{}\cdot 2x=14\cdot\color{blue}{\frac{1}{2}}\color{black}{}&\text{Simplify} \\ x=7&\text{Value of }x\end{array}\nonumber\]
Tareas gráficas y pendientes
Encuentra la pendiente de la línea.
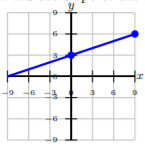
Encuentra la pendiente de la línea.
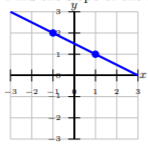
Encuentra la pendiente de la línea.
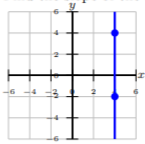
Encuentra la pendiente de la línea.
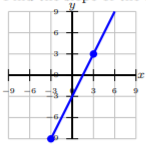
Encuentra la pendiente de la línea.
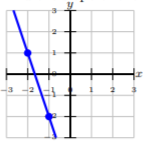
Encuentra la pendiente de la línea.
Encuentra la pendiente de la línea a través de cada par ordenado.
\((−2, 10),\: (−2, −15)\)
\((−15, 10),\: (16, −7)\)
\((10, 18),\: (−11, −10)\)
\((−16, −14),\: (11, −14)\)
\((−4, 14),\: (−16, 8)\)
\((12, −19),\: (6, 14)\)
\((−5, −10),\: (−5, 20)\)
\((−17, 19),\: (10, −7)\)
\((7, −14),\: (−8, −9)\)
\((−5, 7),\: (−18, 14)\)
\((1, 2),\: (−6, −14)\)
\((13, −2),\: (7, 7)\)
\((−3, 6),\: (−20, 13)\)
\((13, 15),\: (2, 10)\)
\((9, −6),\: (−7, −7)\)
\((−16, 2),\: (15, −10)\)
\((8, 11),\: (−3, −13)\)
\((11, −2),\: (1, 17)\)
\((−18, −5),\: (14, −3)\)
\((19, 15),\: (5, 11)\)
Encuentra el valor de\(x\) o\(y\) para que la línea a través de los puntos tenga la pendiente dada.
\((2, 6)\)y\((x, 2)\);\(m =\frac{4}{7}\)
\((−3, −2)\)y\((x, 6)\);\(m = −\frac{8}{5}\)
\((−8, y)\)y\((−1, 1)\);\(m = \frac{6}{7}\)
\((x, −7)\)y\((−9, −9)\);\(m = \frac{2}{5}\)
\((x, 5)\)y\((8, 0)\);\(m = −\frac{5}{6}\)
\((8, y)\)y\((−2, 4)\);\(m = −\frac{1}{5}\)
\((−2, y)\)y\((2, 4)\);\(m = \frac{1}{4}\)
\((x, −1)\)y\((−4, 6)\);\(m = −\frac{7}{10}\)
\((2, −5)\)y\((3, y)\);\(m = 6\)
\((6, 2)\)y\((x, 6)\);\(m = −\frac{4}{5}\)


