2.2: Ecuaciones de líneas
- Page ID
- 117411
En esta sección, discutimos la aplicación de fórmulas para obtener ecuaciones de líneas, graficar líneas y casos especiales. Si podemos identificar algunas propiedades de la línea, es posible que podamos graficar la línea mucho más rápido y más fácil.
La fórmula Inclinación de Inclinación
Uno de esos métodos es encontrar la pendiente y la\(y\) -intercepción de la ecuación. La pendiente se puede representar por\(m\), y la\(y\) -intercepción se puede representar por\((0, b)\), donde\(b\) está el\(y\) -valor en el que la gráfica cruza el\(y\) eje -eje. Cualquier otro punto de la línea puede ser representado por\((x, y)\).
Demuestre la fórmula pendiente-intercepción usando la fórmula de pendiente para la línea que tiene pendiente\(m\),\(y\) -intercepción\((0, b)\) y pasa por el punto\((x, y)\).
Solución
\[\begin{array}{rl}m=\frac{y-b}{x-0}&\text{Simplify} \\ m=\frac{y-b}{x}&\text{Multiply both sides by }x \\ mx=y-b&\text{Add }b\text{ to both sides} \\ mx+b=y \\ y=mx+b&\text{Slope-intercept formula}\end{array}\nonumber\]
La fórmula pendiente-intercepción de una ecuación lineal viene dada por\(y = mx + b\), donde\(m\) está la pendiente y\((0, b)\) es la\(y\) -intercepción.
Encuentra la ecuación de la línea con pendiente\(\frac{3}{4}\) e\(y\) -intercepción\((0, −3)\).
Solución
\[\begin{array}{rl}y=mx+b &m\text{ is the slope, }b\text{ is the }y\text{-intercept} \\ y=\color{blue}{\frac{3}{4}}\color{black}{}x\color{blue}{-3}\color{black}{}&\text{Equation of the line}\end{array}\nonumber\]
Encuentra la ecuación de la línea.
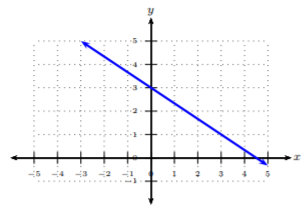
Solución
La\(y\) -intercepción es donde la gráfica cruza el\(y\) eje. Podemos ver, a partir de la gráfica, que la línea cruza el\(y\) eje -en\((0, 3)\). De ahí,\(b = 3\). Para encontrar la pendiente, contamos las unidades de subida y carrera. Podemos ver que subimos\(2\) unidades a la baja y corremos hacia las\(3\) unidades adecuadas. De ahí que la pendiente sea\(−\frac{2}{3}\). Ahora podemos juntar la ecuación de la línea en forma de pendiente-intercepción, donde\(m = −\frac{2}{3}\) y\(b = 3\):
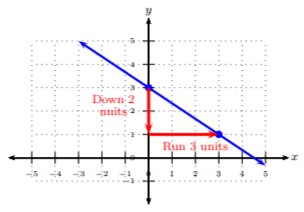
\[y=-\frac{2}{3}x+3\nonumber\]
Líneas en forma de pendiente-intercepción
También podemos identificar la pendiente y\(y\) -interceptar, y graficar la ecuación a partir de una ecuación dada. Sin embargo, necesitamos estar seguros de que la ecuación está en forma de pendiente-intercepción. Si no lo es, tendremos que reescribir la ecuación en forma de pendiente-intercepción, es decir, resolver la ecuación para\(y\). Entonces podemos identificar fácilmente la pendiente y la\(y\) -intercepción.
Escribe la ecuación\(2x − 4y = 6\) en forma de pendiente-intercepción. Encuentra la pendiente y\(y\) -intercepción de la línea.
Solución
\[\begin{array}{rl}2x-4y=6&\text{Isolate the variable term }-4y \\ 2x-4y+\color{blue}{(-2x)}\color{black}{}=6+\color{blue}{(-2x)}\color{black}{}&\text{Simplify} \\ -4y=6-2x &\text{Multiply by the reciprocal of }-4 \\ \color{blue}{-\frac{1}{4}}\color{black}{}\cdot -4y=\color{blue}{-\frac{1}{4}}\color{black}{}\cdot 6-2x\cdot\color{blue}{-\frac{1}{4}}\color{black}{}&\text{Simplify} \\ y=\frac{1}{2}x-\frac{3}{2}&\text{Slope-intercept form}\end{array}\nonumber\]
A continuación, identificamos la pendiente y la\(y\) -intercepción. Si alineamos la forma general pendiente-intercepción con la ecuación que obtuvimos, podemos ver fácilmente\(m\) y\(b\):\[\begin{array}{llll} y&=&mx&+b \\ y&=&\color{blue}{\frac{1}{2}}\color{black}{}x &\color{blue}{-\frac{3}{2}}\end{array}\nonumber\]
De ahí,\(m = \frac{1}{2}\) y\(b = −\frac{3}{2}\), es decir, la pendiente es\(\frac{1}{2}\) y la\(y\) -intercepción es\(−\frac{3}{2}\).
Graficar líneas
Una vez que tenemos una ecuación en forma pendiente-intercepción, podemos graficarla primero trazando la\(y\) -intercepción, luego aplicando la pendiente para encontrar un segundo punto e incluso un tercer punto. Conectamos estos puntos para hacer una línea. Veamos Ejemplo\(\PageIndex{4}\) y graficemos la línea.
Gráfica\(y =\frac{1}{2} x −\frac{3}{2}\) usando la pendiente y\(y\) -intercepción.
Solución
La\(y\) -intercepción, o\(b\), es donde la gráfica cruza el\(y\) eje -eje. Sabemos por Ejemplo\(\PageIndex{4}\) que la\(y\) -intercepción es\(−\frac{3}{2}\) y la línea cruzará el\(y\) -eje en\(\left(0,-\frac{3}{2}\right)\). La pendiente es\(\frac{1}{2}\), y, usando\(\frac{rise}{run}\), necesitamos subir\(1\) unidad ascendente y correr hacia las\(2\) unidades correctas para llegar al siguiente punto. Continuamos el patrón para obtener un tercer punto. Ahora podemos conectar los puntos y crear una línea bien definida. Asegúrate de dibujarlo para llenar la cuadrícula.
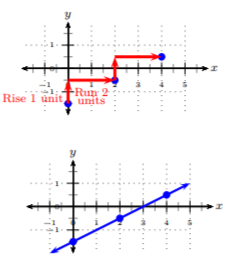
Cuando graficamos una línea trazando puntos de una tabla, obtuvimos tres puntos. De ahí que en Ejemplo\(\PageIndex{5}\), obtuvimos tres puntos y luego dibujamos una línea. Obtener tres puntos en una línea es una práctica común y ayudará a dibujar cualquier línea, incluso los casos especiales.
Antes de nuestro actual sistema de grafismo, la matemática francesa Nicole Oresme, en 1323, sugirió graficar líneas que se parecerían más a gráficos de barras con una pendiente constante.
Escribe la ecuación\(3x + 4y = 12\) en forma de pendiente-intercepción. Encuentra la pendiente e\(y\) intercepción de la línea y luego grafica la línea.
Solución
\[\begin{array}{rl}3x+4y=12&\text{Isolate the variable term }4y \\ 3x+4y+\color{blue}{(-3x)}\color{black}{}=12+\color{blue}{(-3x)}\color{black}{}&\text{Simplify} \\ 4y=12-3x&\text{Multiply by the reciprocal of }4 \\ \color{blue}{\frac{1}{4}}\color{black}{}\cdot 4y=\color{blue}{\frac{1}{4}}\color{black}{}\cdot 12-3x\cdot\color{blue}{\frac{1}{4}}\color{black}{}&\text{Simplify} \\ y=-\frac{3}{4}x+3&\text{Slope-intercept form}\end{array}\nonumber\]
No podemos graficar la línea. Vemos que la\(y\) -intercepción es\(3\) y la línea cruzará el\(y\) eje en\((0, 3)\). La pendiente es\(−\frac{3}{4}\), y, usando\(\frac{rise}{run}\), necesitamos subir\(3\) unidades descendentes y correr hacia las\(4\) unidades correctas para llegar al siguiente punto. Continuamos el patrón para obtener un tercer punto. Ahora podemos conectar los puntos y crear una línea bien definida. Asegúrate de dibujarlo para llenar la cuadrícula.
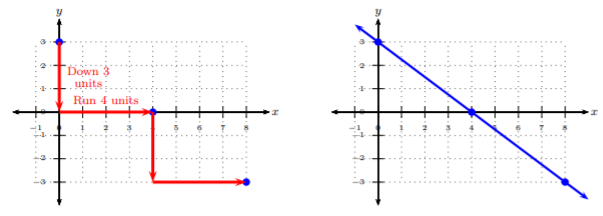
Líneas Verticales y Horizontales
Las líneas con pendiente cero o indefinida pueden hacer que un problema parezca muy diferente. La pendiente cero, o una línea horizontal, simplemente tendrá una pendiente de cero. Entonces, la ecuación simplemente se vuelve\(y = b\) o\(y\) igual a la\(y\) coordenada -de la gráfica. Si tenemos pendiente indefinida, o una línea vertical, la ecuación no se puede escribir en forma de pendiente-intercepción porque la pendiente es indefinida. De ahí que no haya\(y\) en estas ecuaciones. Simplemente haremos\(x\) igual a la\(x\) coordenada -de la gráfica.
Grafica la línea\(x=-4\).
Solución
Ya que\(x = −4\) es una línea vertical, entonces sabemos que esta línea no tiene pendiente y la línea está en su punto más empinado. Cada\(x\) coordenada en esta línea es\(−4\) y la línea no tiene carrera. Podemos graficar esta línea fácilmente trazando tres puntos donde está la\(x\) coordenada\(−4\). Trazemos\((−4, −1),\: (−4, 0),\) y\((−4, 2)\); luego conectemos los puntos con una línea bien definida.
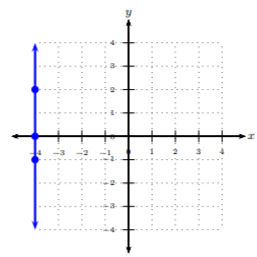
Grafica la línea\(y=1\).
Solución
Ya que\(y = 1\) es una línea horizontal, entonces sabemos que esta línea tiene pendiente cero y la línea está en su punto más plano. Cada\(y\) coordenada en esta línea es\(1\) y la línea no tiene subida. Podemos graficar esta línea fácilmente trazando tres puntos donde está la\(y\) coordenada\(1\). Trazemos\((3, 1),\: (0, 1),\) y\((−2, 1)\); luego conectemos los puntos con una línea bien definida.
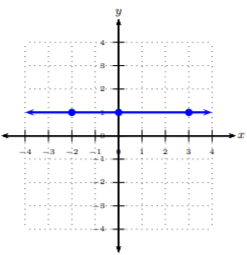
Fórmula de punto-pendiente
La forma pendiente-intercepción tiene la ventaja de ser sencilla de recordar y usar. Sin embargo, tiene una desventaja importante: debemos conocer la\(y\) -intercepción para poder graficar la línea. Generalmente, no conocemos la\(y\) -intercepción, pero, por lo general, conocemos uno o más puntos en la línea que no son la\(y\) -intercepción. En estos casos, no podemos usar la ecuación pendiente-intercepción, por lo que necesitaremos una fórmula más general que nos ayude a graficar líneas. Si la pendiente de una línea es\(m\), y el punto\((x_1, y_1)\) sea un punto particular en la línea, y cualquier otro punto de la línea sea\((x, y)\), entonces podemos usar esto para encontrar esta fórmula general.
\[\begin{array}{rl}m,\: (x_1,y_1),\: (x,y)&\text{Recall slope formula} \\ \frac{y_2-y_1}{x_2-x_1}=m&\text{Plug in values} \\ \frac{y-y_1}{x-x_1}=m&\text{Multiply both sides by }(x-x_1) \\ y-y_1=m(x-x_1)&\text{New formula}\end{array}\nonumber\]
La fórmula de punto-pendiente viene\[y-y_1=m(x-x_1),\nonumber\] dada por la pendiente\(m\) y el punto\((x_1, y_1)\) está en la línea.
Usando la fórmula punto-pendiente, escriba la ecuación de la línea que pasa por el punto\((3, −4)\) con una pendiente de\(\frac{3}{5}\).
Solución
\[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Plug values into point-slope formula} \\ y-(-4)=\frac{3}{5}(x-3)&\text{Simplify signs} \\ y+4=\frac{3}{5}(x-3)&\text{Equation in point-slope form}\end{array}\nonumber\]
A menudo, preferiremos que las respuestas finales se escriban en forma de pendiente-intercepción. Si las direcciones prefieren las ecuaciones de la línea en forma de pendiente-intercepción, podemos distribuir la pendiente, luego resolver para\(y\).
Vamos a reescribir Ejemplo\(\PageIndex{9}\) en forma de pendiente-intercepción:\(y + 4 =\frac{3}{5} (x −3)\)
Solución
\[\begin{array}{rl}y+4=\frac{3}{5}(x-3)&\text{Distribute} \\ y+4=\frac{3}{5}x-\frac{9}{5}&\text{Isolate the variable term }y \\ y+4+\color{blue}{(-4)}\color{black}{}=\frac{3}{5}x-\frac{9}{5}+\color{blue}{(-4)}\color{black}{}&\text{Simplify} \\ y=\frac{3}{5}x-\frac{11}{5}&\text{Slope-intercept form}\end{array}\nonumber\]
Escribe la ecuación de la línea que pasa por el punto\((−6, 2)\) con una pendiente de\(−\frac{2}{3}\) en forma pendiente-intercepción.
Solución
\[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute values into the point-slope formula} \\ y-2=-\frac{2}{3}(x-(-6))&\text{Simplify} \\ y-2=-\frac{2}{3}(x+6)&\text{Distribute} \\ y-2=-\frac{2}{3}x-4&\text{Isolate the variable term }y \\ y-2+\color{blue}{2}\color{black}{}=-\frac{2}{3}x-4+\color{blue}{2}\color{black}{}&\text{Simplify} \\ y=-\frac{2}{3}x-2&\text{Slope-intercept form}\end{array}\nonumber\]
Obtención de una Línea Dada Dos Puntos
Para encontrar la ecuación de una línea, necesitamos conocer la pendiente. Si no se nos da la pendiente, sino solo dos puntos en la línea, entonces completamos algunos trabajos preliminares para obtener la pendiente. Entonces podemos usar la fórmula punto-pendiente como de costumbre para obtener la ecuación de la línea.
Encuentra la ecuación de la línea que pasa por los puntos\((−3, 4)\) y\((−1, −2)\) en forma de pendiente-intercepción
Solución
Dado que se nos dan dos puntos, podemos usar la fórmula de pendiente para obtener la pendiente:\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{Substitute in the ordered-pairs} \\ m=\frac{-2-4}{-1-(-3)}&\text{Simplify} \\ m=\frac{-6}{2} \\ m=-3&\text{Slope}\end{array}\nonumber\]
Ahora que tenemos la pendiente, podemos enchufar y chug la pendiente y uno de los puntos en la fórmula pointslope. Observe que tenemos dos puntos y podemos elegir cualquiera de ellos; los resultados serán los mismos. Vamos a elegir\((−3, 4)\) con la pendiente\(m = −3\).
\[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-4=-3(x-(-3))&\text{Simplify} \\ y-4=-3(x+3)&\text{Distribute} \\ y-4=-3x-9&\text{Isolate the variable term }y \\ y-4+\color{blue}{4}\color{black}{}=-3x-9+\color{blue}{4}\color{black}{}&\text{Simplify} \\ y=-3x-5&\text{Slope-intercept form}\end{array}\nonumber\]
Encuentra la ecuación de la línea a través de los puntos\((6, −2)\) y\((−4, 1)\) en forma de pendiente-intercepción.
Solución
Dado que se nos dan dos puntos, podemos usar la fórmula de pendiente para obtener la pendiente:\[\begin{array}{rl}m=\frac{y_2-y_1}{x_2-x_1}&\text{Substitute in the ordered-pairs} \\ m=\frac{1-(-2)}{-4-6}&\text{Simplify} \\ m=-\frac{3}{10}&\text{Slope}\end{array}\nonumber\]
Ahora que tenemos la pendiente, podemos enchufar y chug la pendiente y uno de los puntos en la fórmula pointslope. Observe que tenemos dos puntos y podemos elegir cualquiera de ellos; los resultados serán los mismos. Vamos a elegir\((−4, 1)\) con la pendiente\(m = −\frac{3}{10}\).
\[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-3=-\frac{3}{10}(x-(-4))&\text{Simplify} \\ y-1=-\frac{3}{10}(x+4)&\text{Distribute} \\ y-1=-\frac{3}{10}x-\frac{6}{5}&\text{Isolate the variable term }y \\ y-1+\color{blue}{1}\color{black}{}=-\frac{3}{10}x-\frac{6}{5}+\color{blue}{1}\color{black}{}&\text{Simplify} \\ y=-\frac{3}{10}x-\frac{1}{5}&\text{Slope-intercept form}\end{array}\nonumber\]
La ciudad de Konigsberg (ahora Kaliningrado, Rusia) tenía un río que fluía a través de la ciudad rompiéndola en varias partes. Había 7 puentes que conectaban las partes de la ciudad. En 1735, Leonhard Euler consideró la cuestión de si era posible cruzar cada puente exactamente una vez y sólo una vez. Resultó que este problema era imposible, pero el trabajo sentó las bases de lo que luego se convertiría en teoría gráfica.
Ecuaciones de Líneas
Escribe la ecuación de la línea en forma de pendiente-intercepción dada la pendiente y la\(y\) -intercepción.
\(m = 2,\: y-intercept = 5\)
\(m = 1,\: y-intercept = −4\)
\(m = −\frac{3}{4},\: y-intercept = −1\)
\(m = \frac{1}{3},\: y-intercept = 1\)
\(m = −6,\: y-intercept = 4\)
\(m = −1,\: y-intercept = −2\)
\(m = −\frac{1}{4},\: y-intercept = 3\)
\(m = \frac{2}{5},\: y-intercept = 5\)
Escribe la ecuación de la línea en forma pendiente-intercepción dada la gráfica o ecuación.
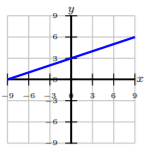
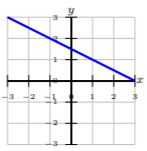
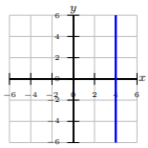
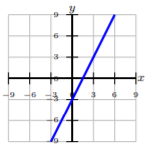
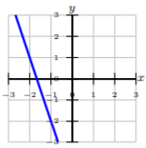
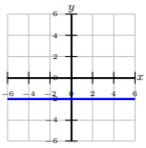
\(x + 10y = −37\)
\(2x + y = −1\)
\(7x − 3y = 24\)
\(x = −8\)
\(y − 4 = −(x + 5)\)
\(y − 4 = 4(x − 1)\)
\(y + 5 = −4(x − 2)\)
\(y + 1 = −\frac{1}{2} (x − 4)\)
\(x − 10y = 3\)
\(6x − 11y = −70\)
\(4x + 7y = 28\)
\(x − 7y = −42\)
\(y − 5 = \frac{5}{2} (x − 2)\)
\(y − 3 = −\frac{2}{3} (x + 3)\)
\(0 = x − 4\)
\(y + 2 = \frac{6}{5} (x + 5)\)
Esboza la gráfica de cada línea.
\(y = \frac{1}{3} x + 4\)
\(y = \frac{6}{5} x − 5\)
\(y = \frac{3}{2} x\)
\(x − y + 3 = 0\)
\(−y − 4 + 3x = 0\)
\(−3y = −5x + 9\)
\(y = − \frac{1}{5} x − 4\)
\(y = − \frac{3}{2} x − 1\)
\(y = − \frac{3}{4} x + 1\)
\(4x + 5 = 5y\)
\(−8 = 6x − 2y\)
\(−3y = 3 − \frac{3}{2}x\)
Escribe la ecuación de la línea en forma de punto-pendiente dado un punto que pasa por la línea y su pendiente.
\((2, 3);\: m =\text{ undefined}\)
\((2, 2);\: m = \frac{1}{2}\)
\((−1, −5);\: m = 9\)
\((−4, 1);\: m = \frac{3}{4}\)
\((0, −2);\: m = −3\)
\((0, −5);\: m = −\frac{1}{4}\)
\((−5, −3);\: m = \frac{1}{5}\)
\((−1, 4);\: m = −\frac{5}{4}\)
\((1, 2);\: m = 0\)
\((2, 1);\: m = −\frac{1}{2}\)
\((2, −2);\: m = −2\)
\((4, −3);\: m = −2\)
\((−1, 1);\: m = 4\)
\((0, 2);\: m = − \frac{5}{4}\)
\((−1, −4);\: m = − \frac{2}{3}\)
Escribe la ecuación de la línea en forma de pendiente-intercepción dado un punto que pasa por la línea y su pendiente.
\((−1, −5) ;\: m = 2\)
\((5, −1) ;\: m = − \frac{3}{5}\)
\((−4, 1) ;\: m = \frac{1}{2}\)
\((4, −2) ;\: m = − \frac{3}{2}\)
\((−5, −3) ;\: m = − \frac{2}{5}\)
\((2, −2) ;\: m = 1\)
\((−3, 4),\: m =\text{ undefined}\)
\((−4, 2) ;\: m = − \frac{1}{2}\)
\((2, −2) ;\: m = −2\)
\((−2, −2) ;\: m = − \frac{2}{3}\)
\((4, −3) ;\: m = − \frac{7}{4}\)
\((−2, 0) ;\: m = − \frac{5}{2}\)
\((3, 3) ;\: m = \frac{7}{3}\)
\((−4, −3);\: m = 0\)
\((−2, −5) ;\: m = 2\)
Escribe la ecuación de la línea en forma de punto-pendiente dados dos puntos en la línea.
\((−4, 3)\text{ and }(−3, 1)\)
\((5, 1)\text{ and }(−3, 0)\)
\((−4, −2)\text{ and }(0, 4)\)
\((3, 5)\text{ and }(−5, 3)\)
\((3, −3)\text{ and }(−4, 5)\)
\((1, 3)\text{ and }(−3, 3)\)
\((−4, 5)\text{ and }(4, 4)\)
\((−4, 1)\text{ and }(4, 4)\)
\((−1, −4)\text{ and }(−5, 0)\)
Escribe la ecuación de la línea en forma de pendiente-intercepción dados dos puntos en la línea.
\((−5, 1)\text{ and }(−1, −2)\)
\((−5, 5)\text{ and }(2, −3)\)
\((4, 1)\text{ and }(1, 4)\)
\((0, 2)\text{ and }(5, −3)\)
\((0, 3)\text{ and }(−1, −1)\)
\((−5, −1)\text{ and }(5, −2)\)
\((1, −1)\text{ and }(−5, −4)\)
\((0, 1)\text{ and }(−3, 0)\)
\((0, 2)\text{ and }(2, 4)\)


