2.3: Líneas paralelas y perpendiculares
- Page ID
- 117410
En esta sección, se discuten las líneas paralelas y perpendiculares. La relación entre líneas paralelas y entre líneas perpendiculares es única, donde la pendiente será de lo más interesante para nosotros en esta sección.
La pendiente de las líneas paralelas y perpendiculares
Encuentra la pendiente de cada línea y compara. ¿Qué tienen de interesante las pistas?
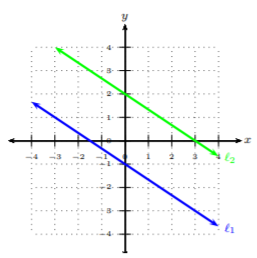
Solución
Mirando\(ℓ_1\), podemos comenzar en\((−3, 1)\) y llegar al siguiente punto en\((0, −1)\). Vemos que bajaremos dos unidades y correremos a las\(3\) unidades adecuadas. De ahí,\(ℓ_1\)'s pendiente es\(−\frac{2}{3}\). Ahora veamos\(ℓ_2\) y obtengamos su pendiente. Empezaremos a las\((0, 2)\) y llegaremos al siguiente punto a las\((3, 0)\). Vemos que bajaremos dos unidades y correremos a las\(3\) unidades adecuadas. De ahí,\(ℓ_2\)'s pendiente es\(−\frac{2}{3}\). Las laderas de\(ℓ_1\) y\(ℓ_2\) son\(−\frac{2}{3}\); tienen la misma pendiente exacta pero diferentes\(y\) -intercepciones.
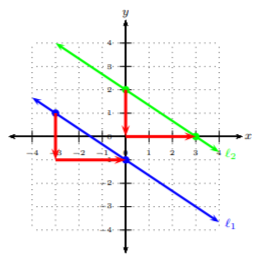
Dejar\(m_1\) y\(m_2\) ser pendientes para líneas\(ℓ_1\) y\(ℓ_2\), respectivamente. Las líneas\(ℓ_1\) y\(ℓ_2\) son paralelas entre sí si tienen la misma pendiente, pero diferentes\(y\) -intercepciones, es decir,\(m_1 = m_2\).
Encuentra la pendiente de cada línea y compara. ¿Qué tienen de interesante las pistas?
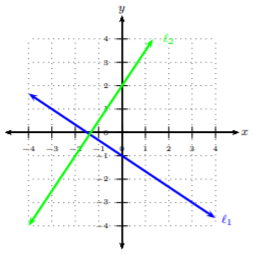
Solución
Mirando\(ℓ_1\), podemos comenzar en\((−3, 1)\) y llegar al siguiente punto en\((0, −1)\). Vemos que bajaremos dos unidades y correremos a las\(3\) unidades adecuadas. De ahí,\(ℓ_1\)'s pendiente es\(−\frac{2}{3}\). Ahora veamos\(ℓ_2\) y obtengamos su pendiente. Empezaremos a las\((−2, −1)\) y llegaremos al siguiente punto a las\((0, 2)\). Vemos que subiremos tres unidades y correremos a las\(2\) unidades adecuadas. De ahí,\(ℓ_2\)'s pendiente es\(\frac{3}{2}\). Las pendientes de\(ℓ_1\) y\(ℓ_2\) son recíprocas negativas, es decir, si se tiene pendiente\(m\), entonces una línea perpendicular a ella tendrá pendiente\(−\frac{1}{m}\). Además, tenga en cuenta que si dos líneas son perpendiculares, crean un ángulo recto en la intersección.
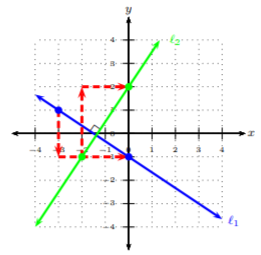
Dejar\(m_1\) y\(m_2\) ser pendientes para líneas\(ℓ_1\) y\(ℓ_2\), respectivamente. Las líneas\(ℓ_1\) y\(ℓ_2\) son perpendiculares entre sí si tienen pendientes recíprocas negativas, es decir,\(ℓ_1\) tiene pendiente\(m_1\) y\(ℓ_2\) tiene pendiente\(m_2 = −\frac{1}{m_1}\).
Encuentra la pendiente de una línea paralela a\(5y − 2x = 7\).
Solución
Necesitamos reescribir la ecuación en forma de pendiente-intersección. Entonces podemos identificar el talud y el talud para una línea paralela a la misma.
\[\begin{array}{rl}5y-2x=7&\text{Isolate the variable term }5y \\ 5y-2x+\color{blue}{2x}\color{black}{}=7+\color{blue}{2x}\color{black}{}&\text{Simplify} \\ 5y=2x+7&\text{Multiply by the reciprocal of }5 \\ \color{blue}{\frac{1}{5}}\color{black}{}\cdot 5y=\color{blue}{\frac{1}{5}}\color{black}{}\cdot 2x+7\cdot\color{blue}{\frac{1}{5}}\color{black}{}&\text{Simplify} \\ y=\frac{2}{5}x+\frac{7}{5}\end{array}\nonumber\]
Vemos que la pendiente de la línea dada es\(\frac{2}{5}\). Por definición, una línea paralela tendrá la misma pendiente\(\frac{2}{5}\).
Encuentra la pendiente de una línea perpendicular a\(3x − 4y = 2\).
Solución
Necesitamos reescribir la ecuación en forma de pendiente-intersección. Entonces podemos identificar la pendiente y la pendiente para una línea perpendicular a la misma.
\[\begin{array}{rl}3x-4y=2&\text{Isolate the variable term }-4y \\ 3x-4y+\color{blue}{(-3x)}\color{black}{}=2+\color{blue}{(-3x)}\color{black}{}&\text{Simplify} \\ -4y=-3x+2&\text{Multiply by the reciprocal of }-4 \\ \color{blue}{-\frac{1}{4}}\color{black}{}\cdot -4y=\color{blue}{-\frac{1}{4}}\color{black}{}\cdot -3x+2\cdot\color{blue}{-\frac{1}{4}}\color{black}{}&\text{Simplify} \\ y=\frac{3}{4}x-\frac{1}{2}\end{array}\nonumber\]
Vemos que la pendiente de la línea dada es\(\frac{3}{4}\). Por definición, una línea perpendicular tendrá una pendiente recíproca negativa\(-\frac{4}{3}\).
Obtener ecuaciones para líneas paralelas y perpendiculares
Una vez que hemos obtenido la pendiente para una línea perpendicular o paralela, es posible encontrar la ecuación completa de la segunda línea si se nos da un punto en la segunda línea.
Encuentra la ecuación de una línea que pasa a través\((4, −5)\) y paralela a\(2x − 3y = 6\).
Solución
Primero, podemos reescribir la línea dada en forma de pendiente-intersección para obtener la pendiente para una línea paralela a ella:\[\begin{array}{rl}2x-3y=6&\text{Isolate the variable term }-3y \\ 2x-3y+\color{blue}{(-2x)}\color{black}{}=6+\color{blue}{(-2x)}\color{black}{}&\text{Simplify} \\ -3y=-2x+6&\text{Multiply by the reciprocal of }-3 \\ \color{blue}{-\frac{1}{3}}\color{black}{}\cdot -3y=\color{blue}{-\frac{1}{3}}\color{black}{}\cdot -2x+6\cdot\color{blue}{-\frac{1}{3}}\color{black}{}&\text{Simplify} \\ y=\frac{2}{3}x-2\end{array}\nonumber\]
Vemos que la pendiente de la línea dada es\(\frac{2}{3}\). Por definición, una línea paralela tendrá la misma pendiente\(\frac{2}{3}\). A continuación, podemos usar la fórmula de punto-pendiente para obtener la ecuación de la línea que pasa\((4, −5)\) con pendiente\(\frac{2}{3}\):\[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-(-5)=\frac{2}{3}(x-4)&\text{Simplify signs} \\ y+5=\frac{2}{3}(x-4)&\text{A line parallel to }2x-3y=6\text{ in point-slope form}\end{array}\nonumber\]
Encuentra la ecuación de la línea, en forma de pendiente-intersección, pasando a través\((6, −9)\) y perpendicular a\(y = −\frac{3}{5}x + 4\).
Solución
Dado que la línea dada está en forma de pendiente-intersección, podemos observar fácilmente la pendiente y la pendiente para una línea perpendicular. Vemos que la pendiente de la línea dada es\(−\frac{3}{5}\). Por definición, una línea perpendicular tendrá una pendiente recíproca negativa\(\frac{5}{3}\). A continuación, podemos usar la fórmula de punto-pendiente para obtener la ecuación, en forma pendiente-intersección, de la línea que pasa\((6, −9)\) con pendiente\(\frac{5}{3}\):\[\begin{array}{rl} y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-(-9)=\frac{5}{3}(x-6)&\text{Simplify signs} \\ y+9=\frac{5}{3}(x-6)&\text{Distribute} \\ y+9=\frac{5}{3}x-10&\text{Isolate the variable term }y \\ y+9+\color{blue}{(-9)}\color{black}{}=\frac{5}{3}x-10+\color{blue}{(-9)}\color{black}{}&\text{Simplify} \\ y=\frac{5}{3}x-19&\text{A line perpendicular to }y=-\frac{3}{5}x+4\text{ in slope-intercept form}\end{array}\nonumber\]
Las líneas con pendientes cero y pendientes indefinidas pueden parecer opuestas porque una línea horizontal tiene pendiente cero y una línea vertical tiene pendiente que es indefinida. Dado que una línea horizontal es perpendicular a una línea vertical, podemos decir, por definición, que las pendientes son recíprocas negativas, es decir,\(m_1 = 0\) implicaría\(m_2 = −\frac{1}{0}\), lo que no está definido.
Encuentra la ecuación de la línea que pasa a través\((3, 4)\) y perpendicular a\(x = −2\).
Solución
Ya que\(x = −2\) es una línea vertical, entonces esta línea tiene pendiente que no está definida. De ahí que una línea perpendicular a ella tendrá pendiente cero, es decir,\(m = 0\). A continuación, podemos usar la fórmula de punto-pendiente para obtener la ecuación, en forma pendiente-intersección, de la línea que pasa\((3, 4)\) con pendiente\(m = 0\):\[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-4=0(x-3)&\text{Distribute} \\ y-4=0&\text{Isolate the variable term }y \\ y-4+\color{blue}{4}\color{black}{}=0+\color{blue}{4}\color{black}{}&\text{Simplify} \\ y=4&\text{A line perpendicular to }x=-2\end{array}\nonumber\]
Ahora bien, como somos conscientes de que una línea perpendicular a una línea vertical es una línea horizontal y nos dieron un punto\((3, 4)\), podríamos haber saltado fácilmente a la ecuación,\(y = 4\).
Tareas de Líneas Paralelas y perpendiculares
Dada la línea, encuentra la pendiente de una línea paralela.
\(y = 2x + 4\)
\(y = 4x − 5\)
\(x − y = 4\)
\(7x + y = −2\)
\(y = − \frac{2}{3} x + 5\)
\(y = − \frac{10}{3} x − 5\)
\(6x − 5y = 20\)
\(3x + 4y = −8\)
Dada la línea, encuentra la pendiente de una línea perpendicular.
\(x=3\)
\(y = −\frac{1}{3} x\)
\(x − 3y = −6\)
\(x + 2y = 8\)
\(y = − \frac{1}{2} x − 1\)
\(y = \frac{4}{5} x\)
\(3x − y = −3\)
\(8x − 3y = −9\)
Encuentra la ecuación de la línea, en forma de punto-pendiente, pasando por el punto y dada la línea para que sea paralela o perpendicular.
\((2, 5)\); paralelo a\(x = 0\)
\((5, 2)\); paralelo a\(y = \frac{7}{5} x + 4\)
\((3, 4)\); paralelo a\(y = \frac{9}{2} x − 5\)
\((1, −1)\); paralelo a\(y = − \frac{3}{4} x + 3\)
\((2, 3)\); paralelo a\(y = \frac{7}{5}x + 4\)
\((−1, 3)\); paralelo a\(y = −3x − 1\)
\((4, 2)\); paralelo a\(x = 0\)
\((1, 4)\); paralelo a\(y = \frac{7}{5} x + 2\)
\((1, −5)\); perpendicular a\(−x + y = 1\)
\((1, −2)\); perpendicular a\(−x + 2y = 2\)
\((5, 2)\); perpendicular a\(5x + y = −3\)
\((1, 3)\); perpendicular a\(−x + y = 1\)
\((4, 2)\); perpendicular a\(−4x + y = 0\)
\((−3, −5)\); perpendicular a\(3x + 7y = 0\)
\((2, −2)\); perpendicular a\(3y − x = 0\)
\((−2, 5)\); perpendicular a\(y − 2x = 0\)
Encuentra la ecuación de la línea, en forma de pendiente-intersección, pasando por el punto y dada la línea para que sea paralela o perpendicular.
\((4, −3)\); paralelo a\(y = −2x\)
\((−5, 2)\); paralelo a\(y = \frac{3}{5} x\)
\((−3, 1)\); paralelo a\(y = − \frac{4}{3} x − 1\)
\((−4, 0)\); paralelo a\(y = − \frac{5}{4} x + 4\)
\((−4, −1)\); paralelo a\(y = − \frac{1}{2}x + 1\)
\((2, 3)\); paralelo a\(y = \frac{5}{2} x − 1\)
\((−2, −1)\); paralelo a\(y = − \frac{1}{2} x − 2\)
\((−5, −4)\); paralelo a\(y = \frac{3}{5} x − 2\)
\((4, 3)\); perpendicular a\(x + y = −1\)
\((−3, −5)\); perpendicular a\(x + 2y = −4\)
\((5, 2)\); perpendicular a\(x = 0\)
\((5, −1)\); perpendicular a\(−5x + 2y = 10\)
\((−2, 5)\); perpendicular a\(−x + y = −2\)
\((2, −3)\); perpendicular a\(−2x + 5y = −10\)
\((4, −3)\); perpendicular a\(−x + 2y = −6\)
\((−4, 1)\); perpendicular a\(4x + 3y = −9\)


