9.6: Gráficas de Funciones Racionales

Última actualización
Guardar como PDF

Page ID: 117512

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Anteriormente, en los capítulos donde discutimos funciones, teníamos una función de la biblioteca\(f(x) = \dfrac{1}{x}\). Recordemos, la gráfica de esta función es

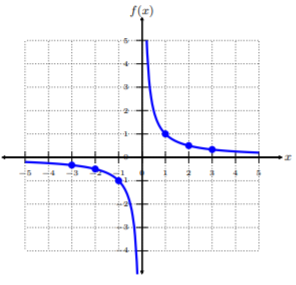
Trazamos algunos puntos que obtuvimos de la tabla y determinamos que el dominio es todo números reales excepto para\(x = 0: \{x|x\neq 0\}\) o\((−∞, 0) ∪ (0, ∞)\). Llamamos a esta función una función racional.

Definición: Función racional

Una función racional,\(R(x)\), es una relación de dos polinomios,\(P(x)\) y\(Q(x)\), de la forma\[R(x)=\dfrac{P(x)}{Q(x)},\nonumber\] donde\(Q(x)\neq 0\).

Nota

En este libro de texto, solo discutimos cuándo\(P(x) = 1\) y cuándo\(Q(x)\) es de la forma\(x^n\), dónde\(n\) es un entero positivo y\[R(x)=\dfrac{1}{x^n}\nonumber\] Para los casos cuando\(P(x)\) es un polinomio distinto de la función constante\(1\) y\(Q(x)\) es un polinomio distinto del poder \(x^n\)se deja para futuras clases de Álgebra.

Investiguemos un poco más estas funciones. Sabemos que el dominio es todo números reales excepto por\(x = 0\), pero veamos la gráfica más de cerca. Observe, en la gráfica de\(f(x)\) arriba, la gráfica no interseca el\(y\) eje. ¿Por qué? Bueno, vamos a establecer\(y = f(x) = 0\) y resolver:

\[f(x)=0=\dfrac{1}{x}\nonumber\]

¿Cuándo es esta fracción cero? Sabemos por secciones anteriores que una fracción es cero cuando el numerador es cero. ¿El numerador alguna vez será cero, es decir,

\[1\stackrel{?}{=}0\nonumber\]

¡No, nunca! Esto significa que no hay valores de\(x\) tal que\(y = 0\), y eso no\(y = 0\) está en el rango de la función.

Esto no es una coincidencia. El hecho de que\(x\neq 0\) y\(y\neq 0\) para la función\(f(x) =\dfrac{1}{x}\) significa que\(f(x)\) tiene asíntotas verticales y horizontales en\(x = 0\) y\(y = 0\), respectivamente.

Definición: Asíntota horizontal y asíntota vertical

Una función,\(R(x)\), tiene una asíntota horizontal en\(y = 0\) y una asíntota vertical en\(x = 0\) cuando\(R(x)\) es de la forma\[\dfrac{1}{x^n}\nonumber\] Denotamos estas asíntotas dibujando líneas discontinuas para líneas\(x = 0\) y\(y = 0\).

Ejemplo 9.6.1

Vamos a regrafiar\(f(x) = \dfrac{1}{x}\) mostrando las asíntotas horizontales y verticales en\(y = 0\) y\(x = 0\), respectivamente.

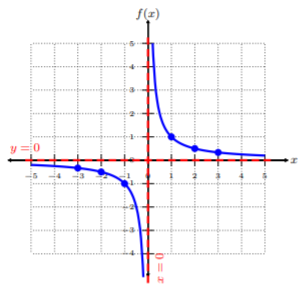
Entonces, vemos que las asíntotas, en rojo, son líneas discontinuas en el\(x\)\(y\) eje y y son las líneas\(y = 0\) y\(x = 0\). El único caso en el que las asíntotas horizontales y verticales se mueven hacia la izquierda o hacia la derecha, y hacia arriba o hacia abajo, respectivamente, es si hay turnos a la función padre\(f(x)\).

Ejemplo 9.6.2

Gráfica\(R(x)=\dfrac{1}{x^2}\).

Solución

Escojamos\(x\) -coordenadas, y busquemos\(y\) -valores correspondientes.

Tabla 9.6.1
\(x\)	\(R(x)=\dfrac{1}{x^2}\)	\((x,R(x))\)
\ (x\) ">\(-3\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{-3}\color{black}{})=\dfrac{1}{(-3)^2}\)	\ ((x, R (x))\) ">\((-3,\dfrac{1}{9})\)
\ (x\) ">\(-2\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{-2}\color{black}{})=\dfrac{1}{(-2)^2}\)	\ ((x, R (x))\) ">\((-2,\dfrac{1}{4})\)
\ (x\) ">\(-1\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{-1}\color{black}{})=1\)	\ ((x, R (x))\) ">\((-1,1)\)
\ (x\) ">\(0\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{0}\color{black}{})=\text{undefined}\)	\ ((x, R (x))\) ">sin punto
\ (x\) ">\(1\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{1}\color{black}{})=1\)	\ ((x, R (x))\) ">\((1,1)\)
\ (x\) ">\(2\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{2}\color{black}{})=\dfrac{1}{2^2}\)	\ ((x, R (x))\) ">\((2,\dfrac{1}{4})\)
\ (x\) ">\(3\)	\ (R (x) =\ dfrac {1} {x^2}\) ">\(f(\color{blue}{3}\color{black}{})=\dfrac{1}{3^2}\)	\ ((x, R (x))\) ">\((3,\dfrac{1}{9})\)

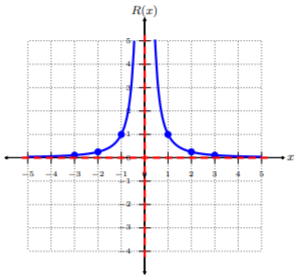
Trazar los pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. El dominio de\(R(x)\) es todos los números reales excepto para\(x = 0: \{x|x\neq 0\}\) o\((−∞, 0)∪(0, ∞)\). Ya que\(R(x)\) tiene asíntotas horizontales y verticales en\(y = 0\) y\(x = 0\), respectivamente, vamos a dibujar las líneas que representan estas asíntotas.

Graficar funciones racionales usando turnos

Echemos un vistazo cuando las gráficas de las funciones racionales contienen desplazamientos horizontales y verticales. Será interesante ver que las asíntotas horizontales y verticales cambian debido a estos cambios.

Desplazamientos horizontales y verticales de funciones racionales

Dada\(R(x)\) es una función racional, un desplazamiento horizontal y un desplazamiento vertical de\(R(x)\) se describen a continuación:

Tabla 9.6.2
	\(R(x-h)\)	\(R(x+h)\)	\(R(x)-k\)	\(R(x)+k\)
Turno	\ (R (x-h)\) ">Desplazamiento horizontal	\ (R (x+h)\) ">Desplazamiento horizontal	\ (R (x) -k\) ">Desplazamiento vertical	\ (R (x) +k\) ">Desplazamiento vertical
Unidades	\ (R (x-h)\) ">Desplazar\(h\) unidades a la derecha	\ (R (x+h)\) ">Desplazar\(h\) unidades a la izquierda	\ (R (x) -k\) "\(k\)>Unidades de desplazamiento hacia abajo	\ (R (x) +k\) "\(k\)>Unidades de desplazamiento hacia arriba
asíntotas	\ (R (x-h)\) ">La asíntota vertical es La asíntota\(x=h\) horizontal es\(y=0\)	\ (R (x+h)\) ">La asíntota vertical es La asíntota\(x=h\) horizontal es\(y=0\)	\ (R (x) -k\) ">La asíntota vertical es La asíntota\(x=0\) horizontal es\(y=k\)	\ (R (x) +k\) ">La asíntota vertical es La asíntota\(x=0\) horizontal es\(y=k\)

Ejemplo 9.6.3

Gráfica\(R(x)=\dfrac{1}{x-2}\).

Solución

Empecemos por tomar la función padre\(f(x) = \dfrac{1}{x}\). Eso lo vemos\(R(x) = f(x − 2)\) porque reemplazamos\(x\) con el factor\((x − 2)\). Al mirar la tabla anterior, vemos que este es un desplazamiento horizontal con\(h = 2\), moviendo\(2\) unidades hacia la derecha, y la asíntota vertical cambia a\(x = 2\).

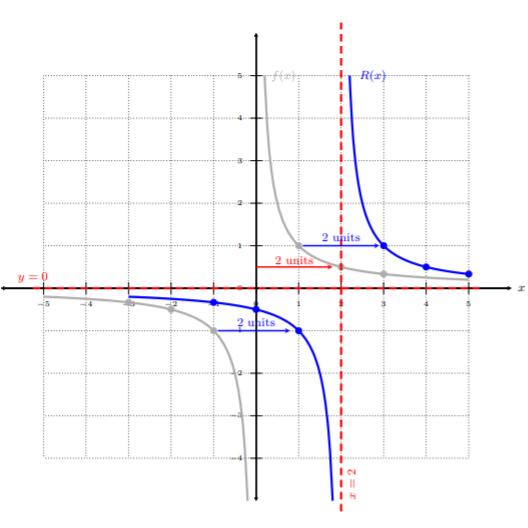
Podemos ver la gráfica gris,\(f(x)\), movió dos unidades a la derecha, además de la asíntota vertical. Recordemos, de la tabla anterior, la asíntota horizontal permanece\(y = 0\). De ahí que la gráfica azul,\(R(x)\), sea la gráfica final después de aplicar los turnos.

Ejemplo 9.6.4

Gráfica\(K(x)=\dfrac{1}{x}+1\).

Solución

Empecemos por tomar la función padre\(f(x) = \dfrac{1}{x}\). Eso lo vemos\(K(x) = f(x) + 1\) porque añadimos\(1\) a\(f(x)\). Al mirar la tabla anterior, vemos que este es un desplazamiento vertical con\(k = 2\), moviendo la\(1\) unidad hacia arriba, y la asíntota horizontal cambia a\(y = 1\).

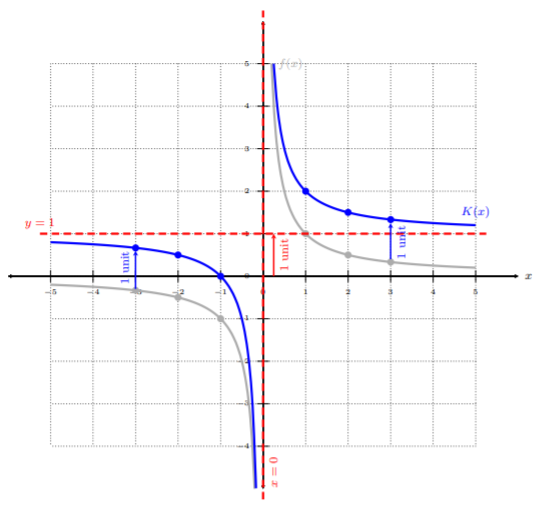
Podemos ver la gráfica gris,\(f(x)\), movió una unidad hacia arriba, además de la asíntota horizontal. Recordemos, de la tabla anterior, la asíntota vertical permanece\(x = 0\). De ahí que la gráfica azul,\(K(x)\), sea la gráfica final después de aplicar los turnos.

Ejemplo 9.6.5

Gráfica\(Q(x)=\dfrac{1}{x+1}-2\).

Solución

Empecemos por tomar la función padre\(f(x) = \dfrac{1}{x}\). Eso lo vemos\(Q(x) = f(x + 1) − 2\) porque reemplazamos\(x\) con el factor\((x + 1)\) y nos restamos\(2\) de\(f(x)\). Al mirar la tabla anterior, vemos que\(Q(x)\) tiene algunos turnos: un desplazamiento horizontal con\(h = −1\),\(1\) unidad móvil hacia la izquierda, un desplazamiento vertical con\(k = −2\),\(2\) unidades móviles hacia abajo, y las asíntotas verticales y horizontales cambian a\(x = −1\) y\(y = −2\), respectivamente.

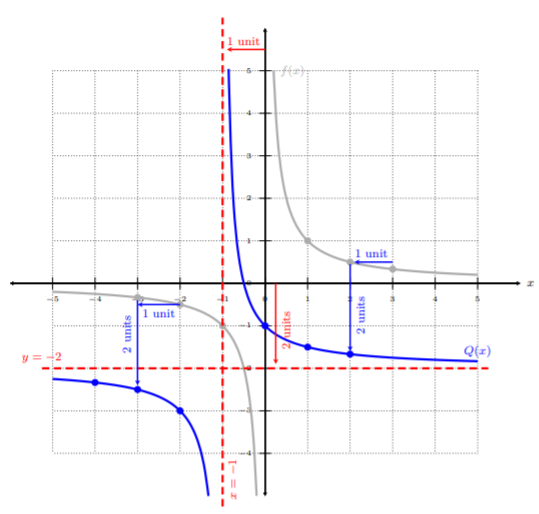
Podemos ver la gráfica gris,\(f(x)\), movió una unidad a la izquierda y\(2\) unidades hacia abajo además de las asíntotas horizontales y verticales. Observe, tuvimos un desplazamiento vertical y horizontal. Trasladamos\(f(x)\) una unidad a la izquierda, luego\(2\) unidades hacia abajo para todos los puntos. Estos cambios hacen que las asíntotas también se muevan. De hecho, la asíntota vertical movió una unidad hacia la izquierda y la asíntota horizontal movió\(2\) unidades hacia abajo. De ahí que la gráfica azul,\(Q(x)\), sea la gráfica final después de aplicar los turnos.

Gráficas Funciones Racionales Tareas

Grafica cada función racional usando la función padre\(f(x) = \dfrac{1}{x}\). Incluir las asíntotas verticales y horizontales.

Ejercicio 9.6.1

\(R(x)=\dfrac{1}{x-1}\)

Ejercicio 9.6.2

\(Q(x)=\dfrac{1}{x+3}\)

Ejercicio 9.6.3

\(S(x)=\dfrac{1}{x}+2\)

Ejercicio 9.6.4

\(T(x)=\dfrac{1}{x}-4\)

Ejercicio 9.6.5

\(U(x)=\dfrac{1}{x+2}-1\)

Ejercicio 9.6.6

\(U(x)=\dfrac{1}{x-3}-2\)

Ejercicio 9.6.7

\(P(x)=\dfrac{1}{x}+3\)

Ejercicio 9.6.8

\(N(x)=\dfrac{1}{x-1}-4\)