12.1: Funciones inversas
- Page ID
- 117504
Funciones uno a uno
Comencemos discutiendo la relación de uno a uno. Las funciones uno a uno son funciones especiales en las que todas las entradas y salidas de una función son distintas, es decir, ninguna de las\(y\) coordenadas\(x\) o se repite.
Una función es uno a uno si dos entradas diferentes en el dominio corresponden a dos salidas diferentes en el rango, es decir,\(f(x_1)\neq f(x_2)\) para cualquiera\(x_1\) y\(x_2\).
Otra forma de determinar uno a uno es asegurarse de que todos los valores x y todos los valores y sean diferentes.
Determinar si la siguiente relación es uno a uno.
\[\{(3,-5), (2,-1), (1,0), (0,7), (-1,8)\}\nonumber\]
Solución
Primero miramos todas las entradas y salidas. Por la definición, necesitamos asegurarnos de que no\(x\) o\(y\) los valores se repitan, es decir, todas\(x\) y las\(y\) coordenadas son únicas. Tenemos
\[x\text{ − values }=3,2,1,0,-1\nonumber\]
y
\[y\text{ − values }=-5,-1,0,7,8\nonumber\]
De ahí que ninguna de las coordenadas se repita, lo que significa que esta relación es uno a uno.
Determinar si la siguiente relación es uno a uno.

Solución
Primero miramos todas las entradas y salidas. Supongamos que el nombre del huracán es el insumo y el año en que ocurrió el huracán es la salida. Por la definición, necesitamos asegurarnos de que no\(x\) o\(y\) los valores se repitan, es decir, todas\(x\) y las\(y\) coordenadas son únicas. Tenemos
\[x \text{− values }=\text{ Ivan, Frances, Jeanne, Isabel, Allison, Charley}\nonumber\]
y
\[y\text{ − values }= 2004, 2004, 2004, 2003, 2001, 2004\nonumber\]
De ahí que ninguna de las\(x\) coordenadas se repita, pero el año 2004 se repite 4 veces en las\(y\) coordenadas, lo que significa que esta relación no es uno-a-uno.
La notación utilizada para las funciones fue introducida por primera vez por el gran matemático suizo, Leonhard Euler, en el siglo XVIII.
Hay una manera gráfica de determinar si una gráfica dada de una función es uno a uno y es por la prueba de línea horizontal. Como usamos la prueba de línea vertical para determinar si una gráfica es una función, usamos la prueba de línea horizontal para determinar si una gráfica de una función es uno a uno.
Si cada línea horizontal intersecta el gráfico de una función\(f\) como máximo un punto, entonces\(f\) es uno a uno.
Determine qué gráficas de las siguientes funciones son de uno a uno.
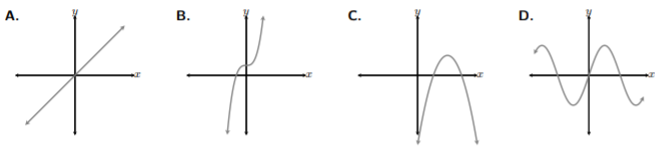
Solución
Empecemos dibujando líneas horizontales a lo largo de cada gráfica y determinemos si la línea se cruza con la gráfica más de una vez. Ahora bien, recordemos, se da que estas gráficas son todas funciones. Es decir, asumimos que estas cuatro funciones han pasado la prueba de línea vertical. Solo necesitamos ver si estas funciones son uno-a-uno aplicando la prueba de línea horizontal.
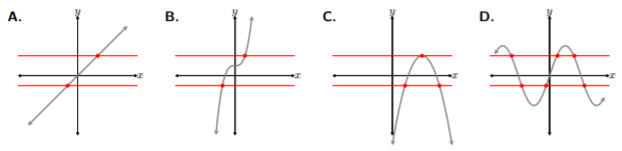
Al observar A. y B., vemos que las líneas horizontales cruzan las gráficas solo una vez, pasando la prueba de líneas horizontales. Si echamos un vistazo a C., la línea superior cruza la gráfica una vez porque solo se cruza en el vértice de la parábola, pero mirando la línea inferior, vemos que la línea horizontal cruza la parábola dos veces. Por lo tanto, C. no pasa la prueba de línea horizontal. Por último, D. tiene sus dos líneas horizontales intersectando la gráfica más de una vez y resultando en fallar la prueba de líneas horizontales. Así, las gráficas A. y B. ambas pasan la prueba de líneas horizontales y son funciones uno-a-uno.
Asegúrese de dibujar líneas horizontales completas, de izquierda a derecha, llenando la cuadrícula y más de una. Es fácil dibujar una línea y detenerse a mitad de camino para concluir que la gráfica pasa la prueba de línea horizontal, como en C. Sin embargo, para la validez de la prueba de línea horizontal, debemos dibujar líneas horizontales completas, de izquierda a derecha, llenando la cuadrícula, y más de una.
Una función y su inversa
Si\(f(x)\) es uno a uno, llamamos a\(f(x)\) una función invertible con pares ordenados\((a, b)\). La función inversa,\(f^{−1} (x)\), es el conjunto de pares ordenados\((b, a)\), es decir,\(y\) -coordenadas y\(x\) -coordenadas conmutan.
Encuentra la inversa de la función uno a uno
\[\{(3, −1),(2, 7),(1, −4),(0, 8),(−1, 5)\}\nonumber\]
Indicar el dominio y el rango de la función inversa.
Solución
Para encontrar la inversa de una función uno-a-uno dada, necesitamos identificar todos\(x\) y\(y\) coordenadas e invertirlos, es decir, por el interruptor de definición,\(y\) -coordenadas y\(x\) -coordenadas. Vamos\(f(x) = \{(3, −1),(2, 7),(1, −4),(0, 8),(−1, 5)\}\). Entonces
\[f^{−1} (x) = \{(−1, 3),(7, 2),(−4, 1),(8, 0),(5, −1)\}\nonumber\]
El dominio de\(f^{−1} (x)\) es\(\{−4, −1, 5, 7, 8\}\) y el rango es\(\{−1, 0, 1, 2, 3\}\).
Dibuja la función inversa de la función uno-a-uno dada.
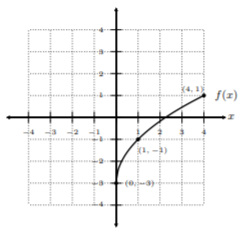
Solución
Usando el mismo razonamiento que hicimos para el Ejemplo 12.1.4 , podemos tomar los pares ordenados bien definidos en la gráfica de\(f(x)\) y cambiar las\(y\) coordenadas\(x\) y. Coloquemos los pares ordenados sobre una mesa:
\[\begin{array}{c|c} x & f(x)\\ \hline 0&-3 \\ 1&-1 \\ 4&1\end{array}\quad\text{this implies that }f^{-1}(x)\text{ is}\quad\begin{array}{c|c} x&f^{-1}(x) \\ \hline -3&0 \\ -1&1 \\ 1&4\end{array}\nonumber\]
Observe, todo lo que hicimos fue cambiar las\(y\) coordenadas\(x\) y de la primera tabla para obtener tres pares ordenados bien definidos\(f^{−1} (x)\). Vamos a graficar estos puntos y conectarlos con una curva suave y agradable:
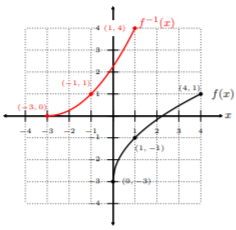
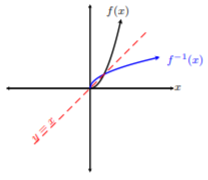
Podemos ver en Example 12.1.5 , que la idea detrás de las funciones invertibles es que\(x\) y las\(y\) coordenadas cambian. De hecho, si miramos aún más de cerca la gráfica de Example 12.1.5 de\(f(x)\) y\(f^{−1} (x)\), podemos ver que\(f^{−1} (x)\) es una imagen especular de\(f(x)\) aproximadamente la línea\(y = x\). Dibujemos la línea\(y = x\) en la gráfica en Ejemplo 12.1.5 :
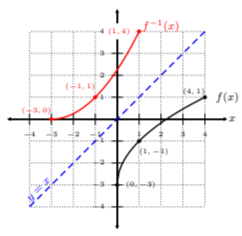
De ahí que la línea\(y = x\) actúe como un espejo,\(f(x)\) y\(f^{−1} (x)\) son reflejos unos de otros alrededor de la línea\(y = x\). ¡Esto no es casualidad!
Recordar. La definición de una composición de dos funciones.
Dejar\(f\) y\(g\) ser funciones de\(x\). Si\(f\) se compone de\(g\), entonces
\[(f\circ g)(x)=f(g(x))\nonumber\]
Decimos que\(f\) está compuesto por\(g\), es decir, sustituimos cada\(x\) in\(f\) con la función\(g(x)\).
\((f\circ g)(x)\)implica que\(x\) está en el dominio de\(g(x)\) y\(g(x)\) está en el dominio de\(f(x)\).
Podemos verificar fácilmente si dos funciones son inversas entre sí mediante el uso de la propiedad de la composición de\(f(x)\) y\(f^{−1} (x)\).
Dada una función\(f(x)\) para ser uno a uno, y\(f^{−1} (x)\)\(f(x)\) es la función inversa, entonces
\[f(f^{-1}(x))=f^{-1}(f(x))=x\nonumber\]
¿Son\(f(x)=\sqrt[3]{3x+4}\) e\(g(x)=\dfrac{x^3-4}{3}\) inversas?
Solución
De la propiedad anterior, podemos utilizar la composición de\(f\) y\(g\) para verificar si\(f(g(x))=x\). Recordemos, si\(f(g(x))=x\), entonces\(f\) y\(g\) son inversos.
\[\begin{aligned}f(\color{blue}{g(x)}\color{black}{)}&=f\left(\color{blue}{\dfrac{x^3-4}{3}}\right) \\ &=\sqrt[3]{\color{black}{\cancel{\color{red}{3}}}\left(\dfrac{x^3-4}{\color{black}{\cancel{\color{red}{3}}}}\right)+4} \\ &=\sqrt[3]{x^3-4+4} \\ &=\sqrt[3]{x^3} \\ &=x\end{aligned}\]
Observe, cuando simplificamos\(f(g(x))\), obtuvimos la expresión simplificada\(x\), es decir,
\[f(g(x))=x\nonumber\]
Así,\(f(x)\) y\(g(x)\) son inversos el uno del otro. Dejamos verificando\(g(f(x)) = x\) al alumno.
¿Son\(h(x)=2x+5\) e\(g(x)=\dfrac{x}{2}-5\) inversas?
Solución
Podemos usar la composición de\(h\) y\(g\) para verificar si\(h(x)\) y\(g(x)\) son inversos. Recordemos, si\(h(g(x))=x\), entonces\(h\) y\(g\) son inversos.
\[\begin{aligned}h(\color{blue}{g(x)})&=h\left(\color{blue}{\dfrac{x}{2}-5}\right) \\ &=2\left(\color{blue}{\dfrac{x}{2}-5}\right)+5 \\ &=\color{blue}{x-10}\color{black}{+5} \\ &=x-5\end{aligned}\]
De ahí\(h(g(x))\neq x\),, y\(h\) y no\(g\) son inversos el uno del otro.
Encontrar el inverso de una función uno a uno algebraicamente
Después de discutir los ejemplos anteriores, podemos encontrar la inversa de un conjunto de elementos, pares ordenados y gráfico, pero ¿cómo encontramos la inversa de una función uno a uno algebraicamente? Por suerte, podemos juntar toda la información y obtener un método para encontrar la inversa de una función uno a uno.
Paso 1. Reemplazar la notación de función con la variable\(y\), es decir, reemplazar\(f(x)\) con\(y\).
Paso 2. Cambiar la variable independiente y\(y\), es decir, cambiar\(x\) y\(y\) variables.
Paso 3. Resolver para\(y\).
Paso 4. Reemplazar\(y\) con la notación de función inversa, es decir, reemplazar\(y\) con\(f^{−1} (x)\).
Paso 5. Verificar la composición de la función original y la función inversa obtenida, es decir,\(f(f^{-1}(x))=x\) o\(f^{-1}(f(x))=x\).
Encuentra la inversa de la función uno a uno\(f(x) = (x + 4)^{3} −2\).
Solución
Sigamos los pasos para obtener la inversa.
Paso 1. Reemplazar\(f(x)\) con\(y\).
\[\begin{aligned}\color{red}{f(x)}&\color{black}{=}(x+4)^3-2 \\ \color{red}{y}&\color{black}{=}(x+4)^3-2\end{aligned}\]
Paso 2. Cambia las\(y\) coordenadas\(x\) y.
\[\begin{aligned}\color{red}{y}&\color{black}{=}(\color{red}{x}\color{black}{+}4)^3-2 \\ \color{red}{x}&\color{black}{=}(\color{red}{y}\color{black}{+}4)^3-2\end{aligned}\]
Paso 3. Resolver para\(y\).
\[\begin{aligned}x&=(\color{red}{y}\color{black}{+}4)^3-2 \\ x+2&=(\color{red}{y}\color{black}{+}4)^3 \\ \sqrt[3]{x+2}&=\color{red}{y}\color{black}{+}4 \\ \sqrt[3]{x+2}-4&=\color{red}{y} \\ y&=\sqrt[3]{x+2}-4\end{aligned}\]
Paso 4. Reemplazar\(y\) con\(f^{-1}(x)\).
\[\begin{aligned}\color{red}{y}&\color{black}{=}\sqrt[3]{x+2}-4 \\ \color{red}{f^{-1}(x)}&\color{black}{=}\sqrt[3]{x+2}-4\end{aligned}\]
Paso 5. Verificar la composición de\(f^{-1}(x)\) y\(f(x)\):\(f(f^{-1}(x))=x\) o\(f^{-1}(f(x))=x\).
\[\begin{aligned}f(\color{blue}{f^{-1}(x)}\color{black}{)}&=f(\color{blue}{\sqrt[3]{x+2}-4}\color{black}{)} \\ &=(\color{blue}{\sqrt[3]{x+2}-\cancel{4}}\color{black}{+}\cancel{4})^3-2 \\ &=(\sqrt[3]{x+2})^3-2 \\ &=x+\cancel{2}-\cancel{2} \\ &=x\end{aligned}\]
Ya que\(f(f^{-1}(x))=x\),, verificamos eso\(f(x)\) y\(f^{−1} (x)\) son, de hecho, inversos.
Así, la función inversa de\(f(x)\) es\(f^{-1}(x)=\sqrt[3]{x+2}-4\).
Encuentra la inversa de la función uno a uno\(g(x)=\dfrac{2x-3}{4x+2}\).
Solución
Sigamos los pasos para obtener la inversa.
Paso 1. Reemplazar\(g(x)\) con\(y\).
\[\begin{aligned}\color{red}{g(x)}&\color{black}{=}\dfrac{2x-3}{4x+2} \\ \color{red}{y}&\color{black}{=}\dfrac{2x-3}{4x+2}\end{aligned}\]
Paso 2. Cambia las\(y\) coordenadas\(x\) y.
\[\begin{aligned}\color{red}{y}&\color{black}{=}\dfrac{2\color{red}{x}\color{black}{-}3}{4\color{red}{x}\color{black}{+}2} \\ \color{red}{x}&\color{black}{=}\dfrac{2\color{red}{y}\color{black}{-}3}{4\color{red}{y}\color{black}{+}2}\end{aligned}\]
Paso 3. Resolver para\(y\).
\[\begin{aligned}x&=\dfrac{2\color{red}{y}\color{black}{-}3}{4\color{red}{y}\color{black}{+}2} \\ (\color{blue}{4y+2}\color{black}{)}\cdot x&=\dfrac{2\color{red}{y}-3}{\cancel{4\color{red}{y}\color{black}{+}2}}\cdot\color{black}{\cancel{(\color{blue}{4y+2})}} \\ 4x\color{red}{y}\color{black}{+}2x&=2\color{red}{y}\color{black}{-}3\end{aligned}\]
En este punto, vemos que hay dos términos con la variable\(\color{red}{y}\). Por lo tanto, debemos aislar los términos con por un\(\color{red}{y}\) lado, y\(\color{red}{y}\) factificar para resolver para\(\color{red}{y}\).
\[\begin{aligned}4x\color{red}{y}\color{black}{+}2x&=2\color{red}{y}\color{black}{-}3 \\ 4x\color{red}{y}\color{black}{-}2\color{red}{y}&\color{black}{=}-2x-3 \\ \color{red}{y}\color{black}{(}4x-2)&=-2x-3 \\ \color{red}{y}&\color{black}{=}\dfrac{-2x-3}{4x-2}\end{aligned}\]
Paso 4. Reemplazar\(y\) con\(g^{-1}(x)\).
\[\begin{aligned}\color{red}{y}&\color{black}{=}\dfrac{-2x-3}{4x-2} \\ \color{red}{g^{-1}(x)}&\color{black}{=}\dfrac{-2x-3}{4x-2}\end{aligned}\]
Paso 5. Verificar la composición de\(g^{−1} (x)\) y\(g(x)\):\(g(g^{-1}(x))=x\) o\(g^{-1}(g(x))=x\). Dejamos este paso para el alumno.
Así, la función inversa de\(g(x)\) es\(g^{−1} (x) = \dfrac{−2x − 3}{4x − 2}\).
Restringir el dominio de una función
En el siguiente ejemplo, discutimos a la ligera la idea de restringir el dominio de una función. Ver, no todas las funciones son una a una, es decir, no todas las gráficas de funciones pasan la prueba de línea horizontal. ¿Podríamos hacer funciones uno a uno? ¿Podríamos forzar una gráfica de una función para que pase la prueba de línea horizontal? ¡Sí! Aquí es donde restringimos el dominio de una función para que una parte de la función sea uno a uno. Tomemos una función simple de la biblioteca,\(f(x) = x^{2}\). Esta función no es uno a uno:
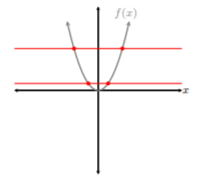
De la figura anterior, la gráfica de\(f(x) = x^{2}\) falla la prueba de línea horizontal. Sin embargo, vamos a restringir el dominio de\(f(x)\) desde\((−∞, ∞)\) a\([0, ∞)\):
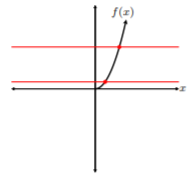
Después de graficar\(f(x) = x^{2}\) en el dominio restringido\([0, ∞)\), podemos ver que\(f(x)\) pasa la prueba de línea horizontal, y, además, es uno a uno. ¡Cuidado! La función\(f(x) = x^{2}\) es solo uno a uno en el dominio restringido\([0, ∞)\).
Encuentra y grafica la inversa de\(f(x) = x^2\) en el dominio restringido\([0, ∞)\).
Solución
Primero encontremos la función inversa de\(f(x)\) en el dominio restringido\([0, ∞)\).
\[\begin{aligned}f(x)&=x^2 \\ y&=x^2 \\ x&=y^2 \\ \pm\sqrt{x}&=y \\ f^{-1}(x)&=\sqrt{x}\end{aligned}\]
Observe, omitimos el valor negativo de\(\sqrt{x}\) porque estamos en el dominio restringido\([0, ∞)\), que no incluye valores negativos. Así, la raíz cuadrada positiva es la única solución en\([0, ∞)\). A continuación, podemos graficar\(f^{-1}(x)=\sqrt{x}\):
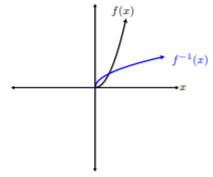
Las gráficas de\(f(x)\) y\(f^{−1} (x)\) son reflexiones unas de otras sobre la línea\(y = x\):
Así, la función inversa de de\(f(x) = x^2\) en el dominio restringido\([0, ∞)\) es\(f^{−1} (x) =\sqrt{x}\).
La restricción del dominio es un concepto útil que se utiliza a lo largo de las matemáticas. Desde funciones trigonométricas inversas hasta el cálculo de integrales de funciones con asíntotas verticales. Algunos de estos conceptos que discutimos temprano en Álgebra son críticos en matemáticas avanzadas.
Funciones inversas Tareas
Indicar si las relaciones dadas son uno-a-uno.
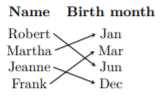
\(\{(−2, 1),(−1, −1),(0, 3),(1, 1),(2, 3)\}\)
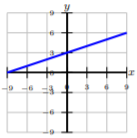
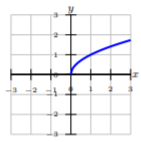
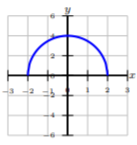
Indicar si las funciones dadas son uno-a-uno. Si no, indica un dominio restringido donde la función puede ser uno a uno.
Indique si las funciones dadas son inversas mediante el uso de la propiedad de composición.
\(\begin{aligned}g(x)&=-x^5 -3 \\ f(x)&=\sqrt[5]{-x-3}\end{aligned}\)
\(\begin{aligned}f(x)&=\dfrac{-x-1}{x-2} \\ g(x)&=\dfrac{-2x+1}{-x-1}\end{aligned}\)
\(\begin{aligned}g(x)&=-10x+5 \\ f(x)&=\dfrac{x-5}{10}\end{aligned}\)
\(\begin{aligned}f(x)&=-\dfrac{2}{x+3} \\ g(x)&=\dfrac{3x+2}{x+2}\end{aligned}\)
\(\begin{aligned}g(x)&=\sqrt[5]{\dfrac{x-1}{2}} \\ f(x)&=2x^5+1\end{aligned}\)
\(\begin{aligned}g(x)&=\dfrac{4-x}{x} \\ f(x)&=\dfrac{4}{x}\end{aligned}\)
\(\begin{aligned}h(x)&=\dfrac{-2-2x}{x} \\ f(x)&=\dfrac{-2}{x+2}\end{aligned}\)
\(\begin{aligned}f(x)&=\dfrac{x-5}{10} \\ h(x)&=10x+5\end{aligned}\)
\(\begin{aligned}f(x)&=\sqrt[5]{\dfrac{x+1}{2}} \\ g(x)&=2x^5-1\end{aligned}\)
\(\begin{aligned}g(x)&=\dfrac{8+9x}{2} \\ f(x)&=\dfrac{5x-9}{2}\end{aligned}\)
Encuentra la función inversa de cada función uno a uno.
\(f(x)=(x-2)^5+3\)
\(g(x)=\dfrac{4}{x+2}\)
\(f(x)=\dfrac{-2x-2}{x+2}\)
\(f(x)=\dfrac{10-x}{5}\)
\(g(x)=-(x-1)^3\)
\(f(x)=(x-3)^3\)
\(g(x)=\dfrac{x}{x-1}\)
\(f(x)=\dfrac{x-1}{x+1}\)
\(g(x)=\dfrac{8-5x}{4}\)
\(g(x)=-5x+1\)
\(g(x)=-1+x^3\)
\(h(x)=\dfrac{4-\sqrt[3]{4x}}{2}\)
\(f(x)=\dfrac{x+1}{x+2}\)
\(f(x)=\dfrac{7-3x}{x-2}\)
\(g(x)=-x\)
\(g(x)=\sqrt[3]{x+1}+2\)
\(f(x)=\dfrac{-3}{x-3}\)
\(g(x)=\dfrac{9+x}{3}\)
\(f(x)=\dfrac{5x-15}{2}\)
\(f(x)=\dfrac{12-3x}{4}\)
\(g(x)=\sqrt[5]{\dfrac{-x+2}{2}}\)
\(f(x)=\dfrac{-3-2x}{x+3}\)
\(h(x)=\dfrac{x}{x+2}\)
\(g(x)=\dfrac{-x+2}{3}\)
\(f(x)=\dfrac{5x-5}{4}\)
\(f(x)=3-2x^5\)
\(g(x)=(x-1)^3+2\)
\(f(x)=\dfrac{-1}{x+1}\)
\(f(x)=-\dfrac{3x}{4}\)
\(g(x)=\dfrac{-2x+1}{3}\)


