12.2: Funciones exponenciales
- Page ID
- 117510
Las funciones exponenciales toman su propio conjunto de técnicas de resolución y simplificación ya que las ecuaciones son un poco diferentes a las anteriores. Por ejemplo, antes teníamos algo así como\(x^2 = 9\), donde podíamos tomar raíz cuadrada de cada lado para resolver. No obstante, si tuviéramos algo así como\(3^x = 9\), notemos que no podemos echar\(x^{\text{th}}\) raíces\(9\) porque se desconoce el índice. No obstante, podemos notar eso\(3^2 = 9\) y concluir que si\(3^x = 3^2\), entonces\(x = 2\). Este es un ejemplo sencillo, pero ¿y si tuviéramos algo un poco más complejo, como\(10.98564^x = 34.9016\)? Entonces el valor de\(x\) no es tan obvio. Estos son los casos que abordamos en esta sección y capítulo.
Una aplicación común de las funciones exponenciales es el crecimiento poblacional. Según el World Factbook de la CIA 2009, el país con mayor tasa de crecimiento poblacional está empatado entre los Emiratos Árabes Unidos (norte de Arabia Saudita) y Burundi (África central) en\(3.69\%\). Hay\(32\) países con tasas de crecimiento negativas, siendo las más bajas las Islas Marianas del Norte (norte de Australia) en\(−7.08\%\).
Una función exponencial es una función de la forma
\[f(x) = a^x,\nonumber\]
donde\(f\) es una función de\(x\),\(a > 0\) y\(a\neq 1\).
Funciones Exponenciales Gráficas
Empecemos a echar un vistazo a las funciones exponenciales mirando sus gráficas.
Trazar\(f(x) = 3^x\) por puntos de trazado. A partir de la gráfica, determinar el dominio de la función.
Solución
Escojamos cinco\(x\) coordenadas y busquemos\(y\) los valores correspondientes. Cada\(x\) -valor es positivo o negativo, y cero. Esta es una práctica común, pero no requerida.
| \(x\) | \(f(x)=3^x\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-2\) | \ (f (x) =3^x\) ">\(f(\color{blue}{-2}\color{black}{)}=3^{\color{blue}{-2}}\color{black}{=}\dfrac{1}{9}\) | \ ((x, f (x))\) ">\(\left(-2,\dfrac{1}{9}\right)\) |
| \ (x\) ">\(-1\) | \ (f (x) =3^x\) ">\(f(\color{blue}{-1}\color{black}{)}=3^{\color{blue}{-1}}\color{black}{=}\dfrac{1}{3}\) | \ ((x, f (x))\) ">\(\left(-1,\dfrac{1}{3}\right)\) |
| \ (x\) ">\(0\) | \ (f (x) =3^x\) ">\(f(\color{blue}{0}\color{black}{)}=3^{\color{blue}{0}}\color{black}{=}1\) | \ ((x, f (x))\) ">\((0,1)\) |
| \ (x\) ">\(1\) | \ (f (x) =3^x\) ">\(f(\color{blue}{1}\color{black}{)}=3^{\color{blue}{1}}\color{black}{=}3\) | \ ((x, f (x))\) ">\((1,3)\) |
| \ (x\) ">\(2\) | \ (f (x) =3^x\) ">\(f(\color{blue}{2}\color{black}{)}=3^{\color{blue}{2}}\color{black}{=}9\) | \ ((x, f (x))\) ">\((2,9)\) |
Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Observe que esta gráfica se eleva de izquierda a derecha, pero, a medida que la gráfica dispara hacia\(−∞\) (a la izquierda), nunca toca el\(x\) eje -ni lo cruza, dando como resultado una asíntota horizontal en\(y = 0\). Como vemos no hay restricciones a la gráfica, el dominio es todo números reales o\((−∞, ∞)\).
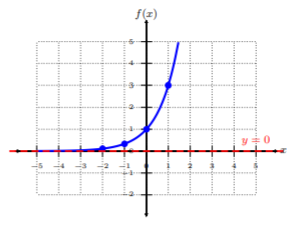
Propiedad 1. El dominio de una función exponencial es todo números reales, es decir,\((−∞, ∞)\).
Propiedad 2. No hay\(x\) -intercepciones; la\(y\) -intercepción está en\((0, 1)\).
Propiedad 3. Si\(a > 1\), entonces la función es una función creciente. Si\(0 < a < 1\), entonces la función es una función decreciente.
Propiedad 4. Hay una asíntota horizontal en\(y = 0\), a menos que haya un desplazamiento vertical.
Una función exponencial nunca cruza el\(x\) eje. De hecho, la función exponencial general no se define en\(f(x) = 0\). Eche un vistazo. Si\(f(x) = 0\), entonces\(f(x) = 0 = a^x\). Pregunte: “¿Por qué valor (es) de\(x\) tal que a se eleva a la potencia de\(x\) y el resultado es cero?” No existe tal\(x\). No podemos elevar un número real positivo a una potencia y el resultado sea cero. En el caso de que una función exponencial cruce el\(x\) eje -eje, entonces eso significa que hubo una transformación a la función exponencial general.
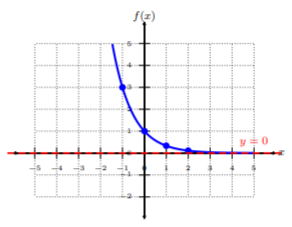
Trazar\(f(x)=\left(\dfrac{1}{3}\right)^x\) por puntos de trazado. A partir de la gráfica, determinar el dominio de la función.
Solución
Escojamos cinco\(x\) coordenadas y busquemos\(y\) los valores correspondientes. Cada\(x\) -valor es positivo o negativo, y cero. Esta es una práctica común, pero no requerida.
| \(x\) | \(f(x)=\dfrac{1}{3}^x\) | \((x,f(x))\) |
|---|---|---|
| \ (x\) ">\(-2\) | \ (f (x) =\ dfrac {1} {3} ^x\) ">\(f(\color{blue}{-2}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{-2}}\color{black}{=}9\) | \ ((x, f (x))\) ">\((-2,9)\) |
| \ (x\) ">\(-1\) | \ (f (x) =\ dfrac {1} {3} ^x\) ">\(f(\color{blue}{-1}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{-1}}\color{black}{=}3\) | \ ((x, f (x))\) ">\((-1,3)\) |
| \ (x\) ">\(0\) | \ (f (x) =\ dfrac {1} {3} ^x\) ">\(f(\color{blue}{0}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{0}}\color{black}{=}1\) | \ ((x, f (x))\) ">\((0,1)\) |
| \ (x\) ">\(1\) | \ (f (x) =\ dfrac {1} {3} ^x\) ">\(f(\color{blue}{1}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{1}}\color{black}{=}\dfrac{1}{3}\) | \ ((x, f (x))\) ">\(\left(1,\dfrac{1}{3}\right)\) |
| \ (x\) ">\(2\) | \ (f (x) =\ dfrac {1} {3} ^x\) ">\(f(\color{blue}{2}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{2}}\color{black}{=}\dfrac{1}{9}\) | \ ((x, f (x))\) ">\(\left(2,\dfrac{1}{9}\right)\) |
Trazar los cinco pares ordenados de la tabla. Para conectar los puntos, asegúrese de conectarlos desde el valor más pequeño hasta\(x\) el valor más grande\(x\), es decir, de izquierda a derecha. Observe que esta gráfica está cayendo de izquierda a derecha, pero, como la gráfica dispara hacia\(∞\) (a la derecha), nunca toca el\(x\) eje -ni lo cruza. Ya que vemos que no hay restricciones a la gráfica, el dominio es todo números reales o\((−∞, ∞)\), y hay una asíntota horizontal en\(y = 0\).
Ecuaciones exponenciales con una base común
Dado que la función exponencial es uno a uno, obtenemos lo siguiente.
Para resolver una ecuación exponencial con una base común en cada lado de la ecuación, usamos el hecho de que si
\[a^m=a^n,\text{ then }m=n.\nonumber\]
Resuelve la ecuación:\(5^{2x+1}=125\)
Solución
Utilizamos el hecho anterior para resolver la ecuación.
\[\begin{array}{rl} 5^{2x+1}=125 & \text{Rewrite }125\text{ as }5^3 \\ 5^{\color{blue}{2x+1}}\color{black}{=}5^{\color{blue}{3}} & \text{Common base, equate exponents} \\ \color{blue}{2x+1}\color{black}{=}\color{blue}{3} & \text{Solve for }x \\ 2x=2 & \text{Divide both sides by }2 \\ x=1 & \text{Solution}\end{array}\nonumber\]
Siempre podemos verificar la respuesta verificando la solución.
\[\begin{aligned} 5^{2x+1}&\stackrel{?}{=}125\quad\text{Plug-n-chug }x=1 \\ 5^{2(\color{blue}{1}\color{black}{)}+1}&\stackrel{?}{=}125\quad\text{Simplify the left side} \\ 5^3&\stackrel{?}{=}125\quad\text{Evaluate }5^3 \\ 125&=125 \quad\checkmark \text{ True} \end{aligned}\]
Ya que obtenemos una declaración verdadera verificando la solución, entonces\(x = 1\) es la solución.
Resuelve la ecuación:\(8^{3x}=32\)
Solución
En este caso, puede que no parezca tan obvio al principio, pero si reescribimos cada base como una base común, entonces podemos aplicar el hecho. Vamos a reescribir cada base como una base común de\(2\).
\[\begin{array} {rl} 8^{3x}=32 & \text{Rewrite }8\text{ as }2^3\text{ and }32\text{ as }2^5 \\ (2^3)^{3x}=2^5 & \text{Multiply exponents }3\text{ and }3x \\ 2^{\color{blue}{9x}} \color{black}{=}2^{\color{blue}{5}} & \text{Common base, equate exponents} \\ \color{blue}{9x}\color{black}{=}\color{blue}{5} & \text{Solve for }x \\ x=\dfrac{5}{9} & \text{Solution}\end{array}\nonumber \]
Siempre podemos verificar la solución, pero dejamos esto en manos del alumno.
Resuelve la ecuación:\(\left(\dfrac{1}{9}\right)^{2x}=3^{7x-1}\)
Solución
En este caso, puede que no parezca tan obvio al principio, pero si reescribimos cada base como una base común, entonces podemos aplicar el hecho. Vamos a reescribir cada base como una base común de\(3\).
\[\begin{array} {rl} \left(\dfrac{1}{9}\right)^{2x}=3^{7x-1} & \text{Rewrite }\dfrac{1}{9}\text{ as }\dfrac{1}{3^2} \\ \left(\dfrac{1}{3^2}\right)^{2x}=3^{7x-1} & \text{Rewrite }\dfrac{1}{3^2}\text{ as }3^{-2} \\ (3^{-2})^{2x}=3^{7x-1} & \text{Multiply exponents }-2\text{ and }2x \\ 3^{\color{blue}{-4x}}\color{black}{=}3^{\color{blue}{7x-1}} & \text{Common base, equate exponents} \\ \color{blue}{-4x}\color{black}{=}\color{blue}{7x-1} & \text{Solve} \\ -11x=-1 & \text{Isolate }x \\ x=\dfrac{1}{11}& \text{Solution}\end{array}\nonumber \]
Siempre podemos verificar la solución, pero dejamos esto en manos del alumno.
Resuelve la ecuación:\(5^{4x}\cdot 5^{2x−1} = 5^{3x+11}\)
Solución
En este caso, puede no parecer tan obvio al principio, pero necesitamos aplicar la regla de producto de exponentes y obtener solo una base común a cada lado de la ecuación para poder aplicar el hecho.
\[\begin{array}{rl} 5^{4x}\cdot 5^{2x-1}=5^{3x+11} & \text{Apply product rule of exponents on the left side} \\ 5^{4x+2x-1}=5^{3x+11}& \text{Simplify the exponent on the left side} \\ 5^{\color{blue}{6x-1}}\color{black}{=}5^{\color{blue}{3x+11}} & \text{Common base, equate exponents} \\ \color{blue}{6x-1}\color{black}{=}\color{blue}{3x+11} & \text{Combine like terms} \\ 3x=12 & \text{Isolate }x \\ x=4& \text{Solution}\end{array}\nonumber\]
Siempre podemos verificar la solución, pero dejamos esto en manos del alumno.
Observe, los ejemplos solo presentan una técnica para resolver ecuaciones exponenciales con una base común. Sin embargo, no todas las ecuaciones exponenciales están escritas con una base común. Por ejemplo, algo así como\(2 = 10^x\) no se puede escribir con una base común. Para resolver problemas donde no podamos reescribir las bases con una base común, necesitamos la función logarítmica, que discutiremos en la siguiente sección.
Funciones Exponenciales Tareas
Grafica cada función exponencial.
\(f(x)=4^x\)
\(x(y)=\left(\dfrac{1}{4}\right)^y\)
\(f(x)=-3^x\)
\(q(r)=-\left(\dfrac{1}{5}\right)^r\)
\(h(n)=\left(\dfrac{1}{2}\right)^n\)
\(g(x)=2^x\)
\(j(x)=-2^x\)
\(k(t)=-\left(\dfrac{1}{2}\right)^t\)
Resuelve la ecuación.
\(3^{1-2n}=3^{1-3n}\)
\(4^{2a}=1\)
\(\left(\dfrac{1}{25}\right)^{-k}=125^{-2k-2}\)
\(6^{2m+1}=\dfrac{1}{36}\)
\(6^{-3x}=36\)
\(64^b=2^5\)
\(\left(\dfrac{1}{4}\right)^x=16\)
\(4^{3a}=4^3\)
\(36^{3x}=216^{2x+1}\)
\(9^{2n+1}=243\)
\(3^{3x-2}=3^{3x+1}\)
\(3^{-2x}=3^3\)
\(5^{m+2}=5^{-m}\)
\(\left(\dfrac{1}{36}\right)^{b-1}=216\)
\(6^{2-2x}=6^2\)
\(4\cdot 2^{-3n-1}=\dfrac{1}{4}\)
\(4^{3k-3}\cdot 4^{2-2k}=16^{-k}\)
\(9^{-2x}\cdot\left(\dfrac{1}{243}\right)^{3x}=243^{-x}\)
\(64^{n-2}\cdot 16^{n+2}=\left(\dfrac{1}{4}\right)^{3n-1}\)
\(5^{-3n-3}\cdot 5^{2n}=1\)
\(4^{2x}=\dfrac{1}{16}\)
\(16^{-3p}=64^{-3p}\)
\(625^{-n-2}=\dfrac{1}{125}\)
\(6^{2r-3}=6^{r-3}\)
\(5^{2n}=5^{-n}\)
\(216^{-3v}=36^{3v}\)
\(27^{-2n-1}=9\)
\(4^{-3v}=64\)
\(64^{x+2}=16\)
\(16^{2k}=\dfrac{1}{64}\)
\(243^{p}=27^{-3p}\)
\(4^{2n}=4^{2-3n}\)
\(625^{2x}=25\)
\(216^{2n}=36\)
\(\left(\dfrac{1}{4}\right)^{3v-2}=64^{1-v}\)
\(\dfrac{216}{6^{-2a}}=6^{3a}\)
\(32^{2p-2}\cdot 8^p=\left(\dfrac{1}{2}\right)^{2p}\)
\(3^{2m}\cdot 3^{3m}=1\)
\(3^{2-x}\cdot 3^{3x}=1\)
\(4^{3r}\cdot 4^{-3r}=\dfrac{1}{64}\)


