13.1: Introducción a las Cónicas
- Page ID
- 117392
Recordemos, un segmento de línea es una línea con dos puntos en cada extremo:

Tomemos este segmento de línea y colóquelo en el plano de coordenadas cartesianas:
Podemos ver que una vez que colocamos el segmento de línea en el plano de coordenadas cartesianas, puntos\(A\) y\(B\) tendremos\(x\) y\(y\) coordenadas. Veamos las coordenadas en lugar de\(A\) y\(B\):
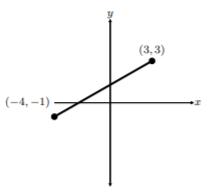
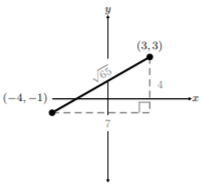
Dado que el segmento de línea tiene extremos en los que se ordenan pares, podemos encontrar la distancia de este segmento de línea. De hecho, si usáramos el Teorema de Pitágoras para encontrar esta longitud, obtendríamos longitud\(\sqrt{65}\):
Teorema de Pitágoras:\(a^2+b^2=c^2\)
\[\begin{aligned}a^2+b^2&=c^2 \\ 7^2+4^2&=c^2 \\ 49+16&=c^2 \\ 65&=c^2 \\ \sqrt{65}&=c\end{aligned}\]
El siguiente paso es encontrar una manera más sofisticada de encontrar la distancia entre dos puntos cualquiera sin importar la ubicación. Tómate un momento para pensarlo. Si los dos puntos están en\((−100, 2000)\) y\((300, 5000)\), ¿vamos a dibujar un triángulo rectángulo tan grande para aplicar el Teorema de Pitágoras? ¡De ninguna manera! Trabajemos de manera más inteligente y no más difícil. Coloquemos dos puntos genéricos donde tuvimos\((−4, −1)\) y\((3, 3)\) y apliquemos el Teorema de Pitágoras para encontrar la hipotenusa:
Teorema de Pitágoras:\(a^2+b^2=c^2\)
\[\begin{aligned}a^2+b^2&=c^2 \\ (x_2-x_1)^2 +(y_2-y_1)^2 &=c^2 \\ \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}&=c\end{aligned}\]
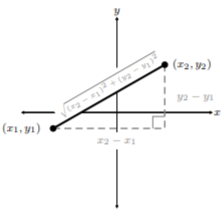
Así, hemos encontrado una fórmula genérica para obtener la distancia entre dos puntos cualesquiera en el plano de coordenadas cartesianas.
La fórmula de distancia
Dados dos puntos,\((x_1, y_1)\) y\((x_2, y_2)\) en un segmento de línea, la distancia\(d\),, de\((x_1, y_1)\) a\((x_2, y_2)\) viene dada por
\[d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\nonumber\]
Encuentra la distancia entre los puntos\((−2, 1)\) y\((1, 2)\). Deja tu respuesta en forma exacta, es decir, tu respuesta debe contener una raíz cuadrada.
Solución
Para encontrar la distancia entre los puntos\((−2, 1)\) y\((1, 2)\), podemos aplicar la fórmula de distancia:
\[\begin{aligned}d&=\sqrt{(1-(-2))^2+(2-1)^2} \\ &=\sqrt{(3)^2+(1)^2} \\ &=\sqrt{9+1} \\ &=\sqrt{10}\end{aligned}\]
Como las indicaciones insistieron dejamos la respuesta en forma exacta, luego nos vamos\(d=\sqrt{10}\).
En el estudio de la geometría euclidiana, llamamos a este tipo (más común) de distancia distancia euclidiana, ya que se deriva del teorema de Pitágoras, que no se sostiene en geometrías no euclidianas. La distancia euclidiana entre dos objetos también puede generalizarse al caso en que los objetos ya no son puntos sino colectores de dimensiones superiores, como las curvas espaciales.
La fórmula del punto medio
Si podemos calcular la distancia entre dos puntos, entonces ciertamente deberíamos poder encontrar el punto medio entre dos puntos. De hecho, lo único que hacemos es calcular el promedio entre las coordenadas correspondientes, es decir, la\(x\) coordenada del punto medio es la media de las dos\(x\) coordenadas dadas en los pares ordenados\((x_1, y_1)\) y\((x_2, y_2)\):
\[x_m=\dfrac{x_1+x_2}{2}\nonumber\]
De igual manera, para la\(y\) coordenada del punto medio, es el promedio de las dos\(y\) coordenadas dadas en los pares ordenados\((x_1, y_1)\) y\((x_2, y_2)\):
\[y_m=\dfrac{y_1+y_2}{2}\nonumber\]
Dados dos puntos,\((x_1, y_1)\) y\((x_2, y_2)\) en un segmento de línea, el punto medio\(m\),, de\((x_1, y_1)\) a\((x_2, y_2)\) viene dado por
\[(x_m,y_m)=\left(\dfrac{x_2+x_1}{2},\dfrac{y_2+y_1}{2}\right)\nonumber\]

Encuentra el punto medio del segmento de línea de\((−4, 2)\) a\((2, −3)\).
Solución
Para encontrar el punto medio entre los puntos\((−4, 2)\) y\((2, −3)\), podemos aplicar la fórmula de punto medio para cada coordenada:
\[\begin{aligned} (x_m,y_m)&=\left(\dfrac{x_2+x_1}{2},\dfrac{y_2+y_1}{2}\right) \\ &=\left(\dfrac{2+(-4)}{2},\dfrac{(-3)+2}{2}\right) \\ &=\left(\dfrac{-2}{2},\dfrac{-1}{2}\right) \\ &=\left(-1,-\dfrac{1}{2}\right)\end{aligned}\]
Así, el punto medio entre\((−4, 2)\) a\((2, −3)\) es\(\left(-1,-\dfrac{1}{2}\right)\).
Construyendo una Cónica
Para entender la idea de cónicas, comenzamos con una forma que nos resulta familiar a todos, un cono circular derecho. Veamos un cono circular derecho:
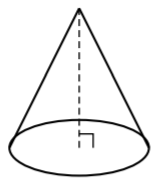
A continuación, podemos tomar un plano y cortar a través del cono para que el plano quede paralelo a la base del cono:
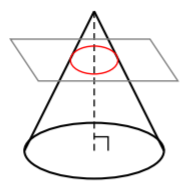
Cuando tomamos el plano y cortamos el cono para que el plano quede paralelo a la base del cono, note que hicimos una forma familiar: el círculo. ¡Guau! Tan genial, ¿verdad? Intentemos con otro. Tomemos el plano y cortemos el cono para que el plano quede paralelo al cono:
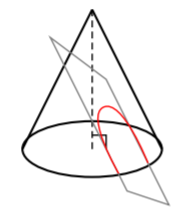
Cuando tomamos el plano y cortamos el cono para que el plano quede paralelo al cono, note que hicimos otra forma familiar. De hecho, conocemos muy bien esta cónica de un capítulo anterior- la parábola. ¡Increíble! Todo lo que hicimos fue tomar un cono circular derecho, cortarlo con un plano, y luego obtener dos cónicas muy conocidas.
Si tomamos un cono circular derecho y cortamos el cono para que el plano quede paralelo a
- la base del cono, luego obtenemos un círculo.
- el lado opuesto del cono, luego obtenemos una parábola.


Hay dos cónicas más, la elipse y la hipérbola, que son otros dos tipos de cortes del cono. Sin embargo, solo discutimos el círculo y la parábola en este libro de texto. La elipse y la hipérbola se discuten en un futuro curso de matemáticas.
Introducción a las tareas de Cónicas
Encuentra el punto medio y la distancia entre los dos puntos dados.
De\((−5, −1)\) a\((5, 2)\)
De\((4, −4)\) a\((2, 5)\)
De\((1, 1)\) a\((−2, −4)\)
De\((5, −2)\) a\((−5, −5)\)
De\((88, −89)\) a\((97, −49)\)
De\((−77, 21)\) a\((−42, 9)\)
Identificar cada cónica por su gráfica o ecuación.




\(y-1=(x-3)^2\)
\(x^2+y^2=25\)
\(y-4=(x-3)^2\)
\(x^2+y^2=16\)


