13.2: Círculos
- Page ID
- 117391
Como comentamos en la sección anterior, vemos que un círculo es simplemente un corte de un cono circular derecho. Vamos a discutir las propiedades del círculo y luego graficarlo.
Un círculo con centro\((h, k)\) y radio\(r > 0\) es el conjunto de todos\((x, y)\) los puntos del plano cuya distancia a\((h, k)\) es\(r\).
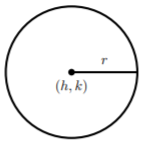
La ecuación estándar de un círculo
Tomemos el círculo y obtengamos la ecuación estándar para un círculo. Tomamos un punto en el círculo\((x, y)\) y encontramos la distancia desde el centro hasta el punto. Ya sabemos que esta distancia es el radio\(r\), pero veamos algebraicamente.
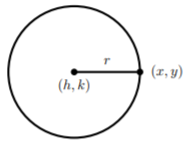
Si aplicamos la fórmula de distancia para encontrar la distancia entre\((h, k)\) y\((x, y)\), obtenemos
\[r=\sqrt{(x-h)^2+(y-k)^2}\nonumber\]
Esto implica que
\[r^2=(x-h)^2+(y-k)^2\nonumber\]
De ahí que al usar la fórmula de distancia, obtuvimos la ecuación estándar de un círculo.
La ecuación estándar de un círculo con centro\((h, k)\) y radio\(r > 0\) es
\[(x-h)^2+(y-k)^2=r^2\nonumber\]
Un círculo centrado en el orogin con radio r viene dado por
\[x^2+y^2=r^2\nonumber\]
y podemos pensar en\(h\) y\(k\) como desplazamientos horizontales y verticales, respectivamente, como hicimos al graficar funciones racionales y cuadráticas.
Escribe la ecuación estándar del círculo con centro\((−2, 3)\) y radio\(5\).
Solución
Para encontrar la ecuación estándar del círculo con centro\((−2, 3)\) y radio\(5\), podemos aplicar la ecuación anterior y sustituirla\(r = 5\),\((h, k) = (−2, 3)\).
\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2 \\ (x-\color{blue}{(-2)}\color{black}{)^2}+(y-\color{blue}{3}\color{black}{)}^2&=\color{blue}{5}\color{black}{^2} \\ (x+2)^2+(y-3)^2&=25\end{aligned}\]
Así, la ecuación estándar del círculo con centro\((−2, 3)\) y radio\(5\) es\((x + 2)^2 + (y − 3)^2 = 25\).
Gráfica de un círculo a partir de la ecuación estándar
A continuación, queremos graficar un círculo a partir de la ecuación estándar. Dado que podemos identificar fácilmente el centro y el radio dada la ecuación estándar de un círculo, podemos graficar fácilmente el círculo.
Grafica el círculo\((x + 2)^2 + (y − 1)^2 = 4\). Encuentra el centro y el radio.
Solución
De la ecuación estándar de un círculo, vemos
\[\begin{aligned} (x-h)^2+(y-k)^2&=r^2 \\ (x+2)^2+(y-1)^2&=4 \\ (x-\color{blue}{(-2)}\color{black}{)}^2+(y-\color{blue}{1}\color{black}{)}^2&=\color{blue}{2}\color{black}{^2}\end{aligned}\]
De mirar lo anterior, vemos\(h = −2\),\(k = 1\), y\(r = 2\). Esto implica que tenemos un círculo centrado en\((−2, 1)\) con radio\(2\). Vamos a graficar esta información.
Primero, trazamos el punto central\((−2, 1)\). Ya que la distancia desde el centro a cualquier punto del círculo es\(2\), entonces contamos dos unidades desde el centro en cada dirección. Podemos conectar los puntos y construir el círculo.
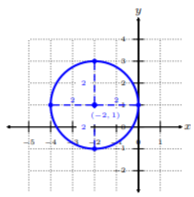
Podemos ver que para poder graficar un círculo, necesitamos reescribir, si es necesario, la ecuación del círculo en la ecuación estándar para identificar el centro y el radio. Entonces podemos trazar fácilmente el centro y contar\(r\) unidades en las cuatro direcciones para construir el círculo.
Reescribir una ecuación de un círculo en la forma de ecuación estándar
¿Qué sucede cuando se nos da una ecuación de un círculo que no está en la forma de la ecuación estándar? Podemos usar el método de completar el cuadrado para reescribir la ecuación en la forma de ecuación estándar.
Recordar. Para completar el cuadrado de una ecuación trinomial de la forma\(x^2 + bx + c = 0\), podemos\(\left(\dfrac{b}{2}\right)^2\) sumar a cada lado de la ecuación.
Paso 1. Agrupe los términos variables en un lado de la ecuación y posicione la constante en el lado opuesto del signo igual.
Paso 2. Completar el cuadrado en ambas variables según sea necesario, es decir, cada término debe verse como\((x − h)^2\) y\((y − k)^2\).
Paso 3. Si hay coeficientes de cada factor, entonces divide cada término por el coeficiente de los cuadrados.
Encuentra el centro y el radio del círculo\(x^2 + y^2 − 6x + 8y + 24 = 0\).
Solución
Para encontrar el centro y el radio del círculo, necesitamos reescribir\(x^2 + y^2 − 6x + 8y + 24 = 0\) en la forma de la ecuación estándar. Sigamos los pasos para obtener la forma de ecuación estándar de la ecuación dada del círculo.
Paso 1. Agrupe las mismas variables en un lado de la ecuación y posicione la constante en el lado opuesto del signo igual.
\[\begin{aligned} x^2+y^2-6x+8y+24&=0 \\ x^2-6x+y^2+8y&=-24\end{aligned}\]
Paso 2. Completar el cuadrado en ambas variables según sea necesario, es decir, cada término debe verse como\((x − h)^2\) y\((y − k)^2\).
\[\begin{aligned}x^2-6x+y^2+8y&=-24 \\ x^2-6x\color{blue}{+9}\color{black}{+}y^2+8y\color{blue}{+16}&\color{black}{=}-24\color{blue}{+9+16} \\ (x-3)^2+(y+4)^2&=1\end{aligned}\]
Paso 3. Divide ambos lados por el coeficiente de los cuadrados.
Dado que los coeficientes de cada factor son 1, entonces no necesitamos reducir ningún coeficiente.
Observe que obtuvimos la ecuación\((x−3)^2+(y+4)^2 = 1\). Esta es la ecuación\(x^2+y^2−6x+8y+24 = 0\) en su forma de ecuación estándar. De ahí que podamos obtener fácilmente el centro y el radio del círculo. De la ecuación estándar del círculo, vemos
\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2 \\ (x-3)^2+(y+4)^2&=1 \\ (x-\color{blue}{3}\color{black}{)}^2+(y-\color{blue}{(-4)}\color{black}{)}^2&=\color{blue}{1}\color{black}{^2}\end{aligned}\]
De mirar lo anterior, vemos\(h = 3\),\(k = −4\), y\(r = 1\). Esto implica que tenemos un círculo centrado en\((3, −4)\) con radio\(1\).
Grafica el círculo en Ejemplo 13.2.3 .
Solución
Como necesitamos graficar el círculo dado en Ejemplo 13.2.3 , podemos usar la ecuación estándar
\[(x-3)^2+(y+4)^2=1,\nonumber\]
donde el círculo está centrado\((3, −4)\) con radio\(1\).
Primero, trazamos el punto central\((3, −4)\). Dado que la distancia desde el centro a cualquier punto del círculo es de 1, entonces contamos una unidad desde el centro en cada dirección. Podemos conectar los puntos y construir el círculo.
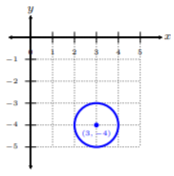
Escribe la ecuación del círculo centrado en el\((10, 7)\) que pasa a través\((11, −2)\).
Solución
Ya que se nos da el centro del círculo con un punto el círculo pasa, entonces podemos usar la ecuación estándar para obtener el radio. Recordemos, el radio es la distancia desde el centro hasta un punto en el círculo.
\[(x-h)^2+(y-k)^2=r^2\nonumber\]
Podemos enchufar y chug\((h, k) = (10, 7)\) y luego\((x, y) = (11, −2)\) encontrar el radio.
\[\begin{aligned} (x-h)^2+(y-k)^2&=r^2 \\ (11-10)^2+(-2-7)^2&=r^2 \\ 1^2+(-9)^2&=r^2 \\ 1+81&=r^2 \\ \color{red}{82}&\color{black}{=}\color{red}{r^2} \\ \sqrt{82}&=r\end{aligned}\]
A pesar de que el radio no es un entero positivo, sigue siendo el radio. De hecho, si pusiéramos el radio en la calculadora, obtendríamos\(\sqrt{82}\approx 9.055\). Al juntar todo esto en la ecuación estándar, obtenemos
\[(x-10)^2+(y-7)^2=\color{red}{82}\nonumber\]
Círculos Testo
Escribe la ecuación estándar del círculo y luego dibuja su gráfica.
Centro\((−1, −5)\), radio\(10\)
Centro\((4, −2)\), radio\(3\)
Centro\(\left(-3,\dfrac{7}{13}\right)\), radio\(1\)
Reescribe la ecuación en la forma de ecuación estándar de un círculo. Identifica el centro y el radio, luego dibuja una gráfica. Si la ecuación no es un círculo, indicar una razón.
\(x^2-4x+y^2+10y=-25\)
\(-2x^2-36x-2y^2-112=0\)
\(x^2+y^2+8x-10y-1=0\)
\(x^2+y^2+5x-y-1=0\)
\(4x^2+4y^2-24y+36=0\)
\(x^2+x+y^2-\dfrac{6}{5}y=1\)
Encuentre la ecuación estándar del círculo que satisfaga los criterios dados.
centro\((3, 5)\), pasa a través\((−1, −2)\)
centro\((3, 6)\), pasa a través\((−1, 4)\)
puntos finales de un diámetro:\((3, 6)\) y\((−1, 4)\)
puntos finales de un diámetro:\(\left(\dfrac{1}{2},4\right)\),\(\left(\dfrac{3}{2},-1\right)\)


