11.5: Aplicaciones
- Page ID
- 112200
El método de cinco pasos
A la hora de resolver problemas prácticos, suele ser más conveniente introducir dos variables en lugar de una sola. Se deben introducir dos variables sólo cuando se puedan encontrar dos relaciones dentro del problema. Cada relación producirá una ecuación, y resultará un sistema de dos ecuaciones en dos variables.
Utilizaremos el método de cinco pasos para resolver estos problemas.
- Introducir dos variables, una por cada cantidad desconocida.
- Busca dos relaciones dentro del problema. Traducir las frases verbales en expresiones matemáticas para formar dos ecuaciones.
- Resolver el sistema resultante de ecuaciones.
- Consulta la solución.
- Escribe una conclusión.
Conjunto de muestras A (problemas numéricos)
La suma de dos números es\(37\). Un número es\(5\) mayor que el otro. ¿Cuáles son los números?
Paso 1:
Dejar un número\(x = \) más pequeño.
Dejar\(y = \) un número mayor.
Paso 2: Hay dos relaciones.
a) La suma es\(37\)
\(x + y = 37\)
b) Uno es\(5\) más grande que el otro.
Paso 3:
\ (\ izquierda\ {\ begin {array} {r}
x + y = 37\\
y = x + 5
\ end {array}\ derecha.\)
Podemos resolver fácilmente este sistema por sustitución. Sustituto\(x + 5\)\(y\) en la ecuación 1.
\ (\ comenzar {alineado}
x + (x + 5) & = 37\\
x + x + 5 &= 37\\
2x + 5 &= 37\\
2x &= 32\\
x &= 16 &\ texto {Entonces,} y = 16 + 5 = 21\\
x &= 16
\ end {alineado}
Paso 4: La suma si\(37\).
\ (\ begin {aligned}
x + y &= 37\\
16 + 21 &= 37\ text {¿Es esto correcto? }\\
37 &= 37\ text {Sí, esto es correcto.}
\ end {alineado}\)
Uno es\(5\) más grande que el otro.
\ (\ begin {aligned}
y &= x + 5\\
21 &= 16 + 5\\
21 &= 21\ text {Sí, esto es correcto.}
\ end {alineado}\)
Paso 5: Los dos números son\(16\) y\(21\).
Conjunto de práctica A
La diferencia de dos números es 9, y la suma de los mismos dos números es 19. ¿Cuáles son los dos números?
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5:
- Contestar
-
Los dos números son 14 y 5.
Problemas de valor y tarifas: problemas de monedas y problemas de mezcla
Los problemas en los Conjuntos de Muestras B y C son problemas de valor. Se les conoce como problemas de valor porque una de las ecuaciones del sistema utilizado para resolverlos se genera considerando un valor, o tasa, o cantidad veces una cantidad.
Juego de Muestras B (Problemas de Monedas)
Un parquímetro contiene 27 monedas consistentes únicamente en monedas de diez centavos y cuartos. Si el medidor contiene $4.35, ¿cuántos de cada tipo de moneda hay?
Paso 1:
Dejar\(D = \) número de monedas de diez centavos.
Dejar\(Q = \) número de cuartos.
Paso 2: Hay dos relaciones.
a) Hay 27 monedas. \(D + Q = 27\).
b) Contribución por diez centavos =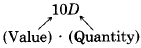
Contribución por trimestres =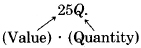
\(10D + 25Q = 435\)
Paso 3:
\ (\ left\ {\ begin {array} {r}
D + Q = 27\\
10D + 25Q = 435
\ end {array}\ right.\)
Podemos resolver este sistema usando eliminación por adición. Multiplica ambos lados de la ecuación (1) por\(-10\) y suma.
\ (\ begin {array} {c}
-10 D-10 Q=-270\\
10 D+25 Q=435\
\ hline 15 Q=165\\
Q=11
\ end {array}\)
Entonces,\ (D + 11 = 27\\
D = 16\)
\(D = 16, Q = 11\)
Paso 4:16 monedas de diez centavos y 11 cuartos son 27 monedas.
\ (\ begin {aligned}
10 (16) + 11 (25) &= 435\ text {¿Es correcto esto? }\\
160 + 275 &= 435\ text {¿Es correcto esto? }\\
435 &= 435\ text {Sí, esto es correcto.}
\ end {alineado}\)
La solución comprueba.
Paso 5: Hay 11 trimestres y 16 dimes.
Set de práctica B
Una bolsa contiene solo monedas de níquel y diez centavos. El valor de la colección es de $2. Si hay 26 monedas en total, ¿cuántas de cada moneda hay?
- Contestar
-
Hay 14 monedas de diez centavos y 12 monedas de níquel.
Conjunto de Muestras C (Problemas de Mezcla)
Un estudiante de química necesita 40 mililitros (ml) de una solución ácida al 14%. Tenía dos soluciones ácidas, A y B, para mezclarlas para formar la solución ácida de 40 ml. La solución ácida A es 10% de ácido y la solución ácida B es 20% de ácido. ¿Cuánto de cada solución se debe usar?
Paso 1:
Dejar\(x = \) número de ml es solución A.
Dejar\(y = \) número de ml de solución B.
Paso 2: Hay dos relaciones
a) La suma del número de ml de las dos soluciones es 40.
\(x + y = 40\).
b) Para determinar la segunda ecuación, dibuje una imagen de la situación
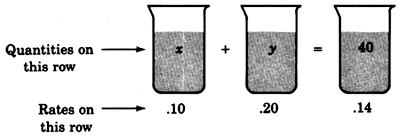
La ecuación sigue directamente del dibujo si utilizamos la idea de cantidad por cantidad.
Paso 3:\(.10x + .20y = .14(40)\)
\ (\ left\ {\ begin {array} {r}
x + y = 40\\
.10x + .20y = .14 (40)
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
x + y = 40\\
.10x + .20y = .14 (40)
\ end {array}\ right.\)
Resuelve este sistema por adición. Primero, elimina los decimales en la ecuación 2 multiplicando ambos lados por 100.
\ (\ left\ {\ begin {array} {r}
x + y = 40\\
10x + 20y = 14 (40)
\ end {array}\ right.\)
Elimine\(x\) multiplicando la ecuación 1 por\(-10\) y luego sumando.
\ (\ begin {array} {c}
-10 x-10 y=-400\\
10 x+20 y=560\
\ hline 10 y=160\
y=16
\ end {array}\)
Entonces,\ (x + 16 = 40\\
x = 24\)
\(x = 24, y = 16\)
Paso 4:24 ml y 16ml para agregar a 40ml.
\ (\ begin {aligned}
10 (24) + 20 (16) &= 560\ text {¿Es correcto esto? }\\
240 + 320 &= 560\ text {¿Es correcto esto? }\\
560 &= 560\ text {Sí, esto es correcto.}
\ end {alineado}\)
La solución comprueba.
Paso 5: El estudiante debe usar 24 ml de solución ácida A y 16 ml de solución ácida B.
Set de práctica C
Un estudiante de química necesita 60 ml de una solución salina al 26%. Tiene dos soluciones salinas, A y B, para mezclarlas para formar la solución de 60 ml. La solución salina A es 30% de sal y la solución salina B es 20% de sal. ¿Cuánto de cada solución se debe usar?
- Contestar
-
El estudiante debe usar 36 ml de solución salina A y 24 ml de solución salina B.
Ejercicios
La suma de dos números es 22. Un número es 6 más que el otro. ¿Cuáles son los números?
- Contestar
-
Los dos números son 14 y 8.
La suma de dos números es 32. Un número es 8 más que el otro. ¿Cuáles son los números?
La diferencia de dos números es 12 y un número es tres veces mayor que el otro. ¿Cuáles son los números?
- Contestar
-
Los dos números son 18 y 6.
La diferencia de dos números es 9 y un número es 10 veces mayor que el otro. ¿Cuáles son los números?
La mitad de la suma de dos números es 14 y la mitad la diferencia es 2. ¿Cuáles son los números?
- Contestar
-
Los números son 16 y 12.
Un tercio de la suma de dos números es 6 y una quinta parte de la diferencia es 2. ¿Cuáles son los números?
Una mezcla de 14 libras de uvas se vende por $3.10. La uva tipo 1 se vende por 25¢ la libra y la uva tipo 2 se vende por 20¢ la libra. ¿Cuántas libras de cada tipo de uva se utilizaron?
- Contestar
-
6 libras de Tipo 1 y 8 libras de Tipo 2.
El costo de 80 litros de una solución de limpieza mezclada es de $28. La solución tipo 1 cuesta 20¢ el litro y la solución tipo 2 cuesta 40¢ el litro. ¿Cuántos litros de cada solución se utilizaron para formar la solución mezclada?
El costo de 42 gramos de un determinado compuesto químico es de $14.40. El químico tipo 1 cuesta 45¢ el gramo y el químico tipo 2 cuesta 30¢ el gramo. ¿Cuántos gramos de cada químico se utilizaron para formar el compuesto?
- Contestar
-
12 gramos de Tipo 1 y 30 gramos de Tipo 2.
A una obra de teatro asistieron 342 personas, algunos adultos y algunos niños. El ingreso para adultos fue de $1.50 y para niños de 75¢. ¿Cuántos adultos y cuántos niños asistieron a la obra?
Se vendieron 200 boletos para la actuación musical anual de una universidad. Los boletos para estudiantes fueron $2.50 y para no estudiantes $3.50. El monto total recaudado fue de 537 dólares. ¿Cuántos no estudiantes compraron boletos para la actuación?
- Contestar
-
37 boletos para no estudiantes.
Un estudiante de química necesita 22 ml de una solución ácida al 38%. Tiene dos soluciones ácidas, A y B, para mezclarlas para formar la solución. La solución ácida A es 40% de ácido y la solución ácida B es 30% de ácido. ¿Cuánto de cada solución se debe usar?
Un estudiante de química necesita 50 ml de una solución salina al 72%. Tiene dos soluciones salinas, A y B, para mezclarlas para formar la solución. La solución salina A es 60% de sal y la solución salina B es 80% de sal. ¿Cuánto de cada solución se debe usar?
- Contestar
-
30 ml de solución al 80%; 20 ml de solución al 60%.
Un químico necesita 2 litros de una solución ácida al 18%. Tiene dos soluciones, A y B, para mezclarlas para formar la solución. La solución ácida A es 10% de ácido y la solución ácida B es 15% de ácido. ¿Puede el químico formar la solución ácida necesaria al 18%? (Verificar por cálculo.) Si el químico localiza una solución ácida al 20%, ¿cuánto se tendría que mezclar con la solución al 10% para obtener la solución necesaria de 2 litros al 18%?
Un químico necesita 3 litros de una solución ácida al 12%. Tiene dos soluciones ácidas, A y B, para mezclarlas para formar la solución. La solución ácida A es 14% de ácido y la solución ácida B es 20% de ácido. ¿Puede el químico formar la solución necesaria al 12%? (Verificar por cálculo.) Si el químico localiza una solución ácida al 4%, ¿cuánto habría que mezclar con la solución ácida del 14% para obtener la solución de 3 litros al 12% necesaria?
- Contestar
-
a) No se puede formar una solución al 12%;
b)\(\dfrac{3}{5}\) litro de solución al 4%.
Un estudiante de química necesita 100 ml de una solución ácida al 16%. Tiene una botella de solución ácida al 20%. ¿Cuánta agua pura y cuánto de la solución al 20% se debe mezclar para diluir la solución ácida al 20% a una solución ácida al 16%?
Un estudiante de química necesita 1 litro de una solución salina al 78%. Ella tiene una botella de solución salina al 80%. ¿Cuánta agua pura y cuánto de la solución salina al 80% se debe mezclar para diluir la solución salina al 80% a una solución salina del 78%?
- Contestar
-
25 ml de agua pura; 975 ml de solución salina al 80%.
25 ml de agua pura; 975 ml de solución salina al 80%.
Un banco infantil contiene 78 monedas. Las monedas son sólo centavos y monedas de níquel. Si el valor de las monedas es de $1.50, ¿cuántas de cada moneda hay?
- Contestar
-
18 monedas de cinco centavos; 60 centavos.
Ejercicios para revisión
Simplificar\(\dfrac{x^{n + 6}}{x^2}\)
Encuentra el producto:\((3x - 5)^2\)
- Contestar
-
\(9x^2 - 30x + 25\)
Encuentra la diferencia:\(\dfrac{2x - 1}{x^2 + x - 6} - \dfrac{x + 2}{x^2 + 5x + 6}\)
Utilice el método de sustitución para resolver
\ (\ izquierda\ {\ begin {array} {r}
4x - y = 3\\
2x - 5 = 15
\ end {array}\ derecha.\)
- Contestar
-
\((0,−3)\)
Utilice el método de adición para resolver
\ (\ left\ {\ begin {array} {r}
3x + 4y = -7\\
4x - 5y = 1
\ end {array}\ right.\)