2.5: Aplicaciones de ecuaciones lineales
- Page ID
- 110140
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Identificar palabras y frases clave, traducir oraciones a ecuaciones matemáticas y desarrollar estrategias para resolver problemas.
- Resolver problemas de palabras que involucran relaciones entre números.
- Resolver problemas de geometría que involucran perímetro.
- Resolver problemas de porcentaje y dinero incluyendo intereses simples.
- Configure y resuelva problemas de movimiento uniforme.
Palabras clave, traducción y estrategia
El álgebra simplifica el proceso de resolución de problemas del mundo real. Esto se hace usando letras para representar incógnitas, replanteando problemas en forma de ecuaciones y ofreciendo técnicas sistemáticas para resolver esas ecuaciones. Para resolver problemas utilizando álgebra, primero traduzca la redacción del problema en enunciados matemáticos que describan las relaciones entre la información dada y las incógnitas. Por lo general, esta traducción a declaraciones matemáticas es el paso difícil en el proceso. La clave de la traducción es leer atentamente el problema e identificar ciertas palabras y frases clave.
| Palabras clave | Traducción |
|---|---|
| Suma, incrementada en, más de, más, sumada a, total | \(+\) |
| Diferencia, disminuida por, restada de, menos, menos | \(-\) |
| Producto, multiplicado por, de, veces, dos veces | \(*\) |
| Cociente, dividido por, ratio, per | \(/\) |
| Es, total, resultado | \(=\) |
Aquí hay algunos ejemplos de frases clave traducidas.
| Frases Clave | Traducción |
|---|---|
| La suma de un número y 7. |
\(x+7\) |
| Siete más que un número. | |
| La diferencia de un número y 7. |
\(x-7\) |
| Siete menos que un número. | |
| Siete restaron de un número. | |
| El producto de 2 y un número. |
\(2x\) |
| Dos veces un número. | |
| La mitad de un número. | \(\frac{1}{2}x\) |
| El cociente de un número y 7. | \(\frac{x}{7}\) |
Al traducir oraciones en declaraciones matemáticas, asegúrese de leer la oración varias veces e identificar las palabras y frases clave.
Ejemplo\(\PageIndex{1}\)
Traducir:
Cuatro menos del doble de algún número es\(16\).
Solución:
Primero, elija una variable para el número desconocido e identifique las palabras y frases clave. Vamos a\(x\) representar lo desconocido indicado por “algún número”.
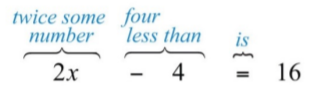.png)
Figura\(\PageIndex{1}\)
Recuerda que la resta no es conmutativa. Por esta razón, tenga cuidado a la hora de establecer diferencias. En este ejemplo,\(4−2x=16\) es una traducción incorrecta.
Respuesta:
\(2x−4=16\)
Es importante identificar primero la variable— dejar que x represente... —y declarar en palabras cuál es la cantidad desconocida. Este paso no sólo hace que tu trabajo sea más legible sino que también te obliga a pensar en lo que buscas. Por lo general, si sabes lo que te piden encontrar, entonces la tarea de encontrarlo es alcanzable.
Ejemplo\(\PageIndex{2}\)
Traducir:
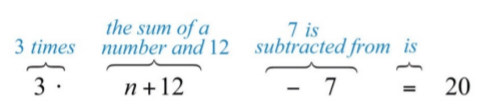
Cuando\(7\) se resta de\(3\) veces la suma de un número y\(12\), el resultado es\(20\).
Solución:
Vamos a\(n\) representar el número desconocido.
.png)
Figura\(\PageIndex{2}\)
Respuesta:
\(3(n+12)−7=20\)
Para entender por qué se necesitan paréntesis, estudie las estructuras de las siguientes dos oraciones y sus traducciones:
| “3 veces la suma de un número y 12” | \(3(n+12)\) |
| “la suma de 3 veces un número y 12” | \(3n+12\) |
La clave es enfocarse en la frase “3 veces la suma”. Esto nos impulsa a agrupar la suma entre paréntesis y luego multiplicar por 3. Una vez que una aplicación se traduce en una ecuación algebraica, resuelva usando las técnicas que haya aprendido.
Lineamientos para Configurar y Resolver Problemas de la Palabra
- Paso 1: Lee el problema varias veces, identifica las palabras y frases clave, y organiza la información dada.
- Paso 2: Identificar las variables asignando una letra o expresión a las cantidades desconocidas.
- Paso 3: Traducir y configurar una ecuación algebraica que modele el problema.
- Paso 4: Resolver la ecuación algebraica resultante.
- Paso 5: Finalmente, contesta la pregunta en forma de oración y asegúrate de que tenga sentido (verifícalo).
Por ahora, configura todas tus ecuaciones usando solo una variable. Evita dos variables buscando una relación entre las incógnitas.
Problemas que involucran relaciones entre números reales
Clasificamos las aplicaciones que involucran relaciones entre números reales ampliamente como problemas numéricos. Estos problemas a veces se pueden resolver usando algunas aritméticas creativas, adivinanzas y comprobaciones. Resolver de esta manera no es una buena práctica y debe evitarse. Comience trabajando a través de los pasos básicos señalados en los lineamientos generales para la solución de problemas verbales.
Ejemplo\(\PageIndex{3}\)
Un entero mayor es\(2\) menor que\(3\) veces un número entero menor. La suma de los dos enteros es\(18\). Encuentra los enteros.
Solución:
Identificar variables: Comience asignando una variable al entero más pequeño.
Let\(x\) representar el entero más pequeño.
Usa la primera oración para identificar el entero más grande en términos de la variable\(x\): “Un entero mayor es 2 menos que 3 veces más pequeño”.
Let\(3x-2\) representar el entero más grande.
Configura una ecuación: Agrega las expresiones que representan los dos enteros, y establece la expresión resultante igual a\(18\) como se indica en la segunda oración: “La suma de los dos enteros es”\(18\).
\(x+(3x-2)=18\)
Resolver: Resuelve la ecuación para obtener el entero más pequeño\(x\).
\(\begin{aligned} x+(3x-2)&=18 \\ x+3x-2&=18 \\ 4x-2&=18 \\ 4x-2\color{Cerulean}{+2}&=18\color{Cerulean}{+2} \\ 4x&=20 \\ \frac{4x}{\color{Cerulean}{4}}&=\frac{20}{\color{Cerulean}{4}} \\ x&=5 \end{aligned}\)
Sustituto posterior: Use la expresión\(3x−2\) para encontrar el entero más grande, esto se llama volver a sustituir.
\(3x-2=3(\color{OliveGreen}{5}\color{black}{)-2=15-2=13}\)
Responde a la pregunta: Los dos enteros son\(5\) y\(13\).
Cheque:\(5 + 13 = 18\). La respuesta tiene sentido.
Ejemplo\(\PageIndex{4}\)
La diferencia entre dos enteros es\(2\). El entero más grande es\(6\) menos del doble del menor. Encuentra los enteros.
Solución:
Usa la relación entre los dos enteros en la segunda oración, “El entero mayor es 6 menos que el doble del menor”, para identificar las incógnitas en términos de una variable.
Let\(x\) representar el entero más pequeño.
Let\(2x-6\) representar el entero más grande.
Dado que la diferencia es positiva, resta el entero más pequeño del mayor.
\((2x-6)-x=2\)
Resolver.
\(\begin{aligned} \color{OliveGreen}{2x}\color{black}{-6}\color{OliveGreen}{-x}&=2 \\ x-6&=2 \\ x-6\color{Cerulean}{+6}&=2\color{Cerulean}{+6} \\ x&=8 \end{aligned}\)
Se usa\(2x − 6\) para encontrar el entero más grande.
\(2x-6=2(\color{Cerulean}{8}\color{black}{)-6=16-6=10}\)
Respuesta:
Los dos enteros son\(8\) y\(10\). Estos enteros resuelven claramente el problema.
Vale la pena mencionar nuevamente que a menudo puedes encontrar soluciones a problemas simples adivinando y verificando. Esto es así porque los números son elegidos para simplificar el proceso de resolución, de manera que los pasos algebraicos no sean demasiado tediosos. Aprendes a configurar ecuaciones algebraicas con problemas más fáciles, para que puedas usar estas ideas para resolver problemas más difíciles posteriormente.
Ejemplo\(\PageIndex{5}\)
La suma de dos enteros pares consecutivos es\(46\). Encuentra los enteros.
Solución:
La frase clave en la que enfocarse es “enteros pares consecutivos”.
Let\(x\) representar el primer entero par.
Let\(x+2\) representar el siguiente número entero par.
Agregue los enteros pares y configúrelos iguales a\(46\).
\(x+(x+2)=46\)
Resolver.
\(\begin{aligned}\color{OliveGreen}{x+x}\color{black}{+2}&=46\\2x+2&=46\\2x+2\color{Cerulean}{-2}&=46\color{Cerulean}{-2}\\2x&=44\\x&=22 \end{aligned}\)
\(x + 2\)Utilízalo para encontrar el siguiente número entero par.
\(x+2=\color{Cerulean}{22}\color{black}{+2=24}\)
Respuesta:
Los enteros pares consecutivos son\(22\) y\(24\).
Debe quedar claro que los enteros pares consecutivos están separados por dos unidades. Sin embargo, puede que no quede tan claro que los enteros impares también lo sean.
.png)
Figura\(\PageIndex{3}\)
Ejemplo\(\PageIndex{6}\)
La suma de dos enteros impares consecutivos es\(36\). Encuentra los enteros.
Solución:
La frase clave en la que enfocarse es “enteros impares consecutivos”.
Let\(x\) representa el primer entero impar.
Let\(x+2\) representa el siguiente entero impar.
Agregue los dos enteros impares y establezca la expresión igual a\(36\).
\(x+(x+2)=36\)
Resolver.
\(\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+2}&=36 \\ 2x+2&=36 \\ 2x+2\color{Cerulean}{-2}&=36\color{Cerulean}{-2} \\ 2x&=34 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{34}{\color{Cerulean}{2}} \\ x&=17 \end{aligned}\)
\(x + 2\)Utilízalo para encontrar el siguiente entero impar.
\(x+2=\color{OliveGreen}{17}\color{black}{+2=19}\)
Respuesta:
Los enteros impares consecutivos son\(17\) y\(19\).
La configuración algebraica para problemas de enteros pares e impares es la misma. Un error común es usar\(x\) y\(x + 3\) al identificar las variables para enteros impares consecutivos. Esto es incorrecto porque sumar 3 a un número impar produce un número par: por ejemplo,\(5 + 3 = 8\). Es muy probable que una configuración incorrecta conduzca a una respuesta decimal, lo que puede ser una indicación de que el problema se configuró incorrectamente.
Ejemplo\(\PageIndex{7}\)
La suma de tres enteros consecutivos es\(24\). Encuentra los enteros.
Solución:
Los enteros consecutivos están separados por una unidad.
Let\(x\) representar el primer entero.
Let\(x+1\) representar el siguiente entero.
Let\(x+2\) representar el tercer entero.
Agregue los enteros y establezca la suma igual a\(24\).
\(x+(x+1)+(x+2)=24\)
Resolver.
\(\begin{aligned} \color{OliveGreen}{x+x}\color{black}{+1}\color{OliveGreen}{+x}\color{black}{+2}&=24\\ 3x+3&=24 \\ 3x+3\color{Cerulean}{-3}&=24\color{Cerulean}{-3} \\ 3x&=21 \\ x&=7 \end{aligned}\)
Volver sustituto para encontrar los otros dos enteros.
\(x+1=\color{OliveGreen}{7}\color{black}{+1=8}\)
\(x+2=\color{OliveGreen}{7}\color{black}{+2=9}\)
Respuesta:
Los tres enteros consecutivos son\(7, 8\) y\(9\), dónde\(7 + 8 + 9 = 24\).
Ejercicio\(\PageIndex{1}\)
La suma de tres enteros impares consecutivos es\(87\). Encuentra los enteros.
- Contestar
-
Los enteros son\(27, 29\), y\(31\).
Problemas de geometría (perímetro)
Recordemos que el perímetro de un polígono es la suma de las longitudes de todos los bordes exteriores. Además, es útil revisar las siguientes fórmulas perimetrales\((π≈3.14159)\).
| Perímetro de un rectángulo: | \(P=2l+2w\) |
| Perímetro de un cuadrado: | \(P=4s\) |
| Perímetro de un triángulo: | \(P=a+b+c\) |
| Perímetro de un círculo (circunferencia): | \(C=2\pi r\) |
Ten en cuenta que estás buscando una relación entre las incógnitas para que puedas configurar ecuaciones algebraicas usando solo una variable. Cuando se trabaja con problemas de geometría, a menudo es útil dibujar una imagen.
Ejemplo\(\PageIndex{8}\)
Un rectángulo tiene\(64\) pies de medición perimetral. El largo es\(4\) pies más que\(3\) veces el ancho. Encuentra las dimensiones del rectángulo.
Solución:
La frase “La longitud es de 4 pies más de 3 veces el ancho” da la relación entre las dos variables.
.png)
Figura\(\PageIndex{4}\)
Dejar\(w\) representar el ancho del rectángulo.
Dejar\(3w+4\) representar la longitud.
La frase “Un rectángulo tiene un perímetro que mide\(64\) pies” sugiere una configuración algebraica. Sustituya\(64\) el perímetro y la expresión por la longitud en la fórmula apropiada de la siguiente manera:
\(\begin{aligned} P&=\:\:\:\:\quad 2l + 2w \\ \color{Cerulean}{\downarrow}&\:\:\:\qquad\quad\color{Cerulean}{\downarrow} \\ \color{OliveGreen}{64}&=2(\color{OliveGreen}{3w+4}\color{black}{)+2w} \end{aligned}\)
Una vez que haya configurado una ecuación algebraica con una variable, resuelva para el ancho,\(w\).
\(\begin{aligned} 64&=\color{OliveGreen}{6w}\color{black}{+8+}\color{OliveGreen}{2w} \\ 64&=8w+8 \\ 64\color{Cerulean}{-8}&=8w+8\color{Cerulean}{-8} \\ 56&=8w \\ \frac{56}{\color{Cerulean}{8}}&=\frac{8w}{\color{Cerulean}{8}} \\ 7&=w \end{aligned}\)
\(3w + 4\)Utilízalo para encontrar la longitud.
\(l=3w+4=3(\color{OliveGreen}{7}\color{black}{)+4=21+4=25}\)
Respuesta:
El rectángulo mide\(7\) pies a\(25\) pies. Para verificar, agregue todos los lados:
\(P=7\text{ ft+}7\text{ ft+}25\text{ ft+}25\text{ ft}=64\text{ ft}\)
Ejemplo\(\PageIndex{9}\)
Dos lados de un triángulo son\(5\) y\(7\) pulgadas más largos que el tercer lado. Si el perímetro mide\(21\) pulgadas, encuentra la longitud de cada lado.
.png)
Figura\(\PageIndex{5}\)
Solución:
La primera frase describe las relaciones entre las incógnitas.
Dejar\(x\) representar la longitud del tercer lado.
Dejar\(x+5\) y\(x+7\) representar las longitudes de los otros dos lados.
Sustituir estas expresiones en la fórmula apropiada y utilizar\(21\) para el perímetro\(P\).
\(\begin{aligned} P&=a+b+c \\ \color{OliveGreen}{21}&=\color{OliveGreen}{x}\color{black}{+}\color{OliveGreen}{(x+5)}\color{black}{+}\color{OliveGreen}{(x+7)} \end{aligned}\)
Ahora tienes una ecuación con una variable que resolver.
\(\begin{aligned} 21&=x+x+5+x+7 \\ 21&=3x+12 \\ 21\color{Cerulean}{-12}&=3x+12\color{Cerulean}{-12} \\ 9&=3x\\ \frac{9}{\color{Cerulean}{3}}&=\frac{3x}{\color{Cerulean}{3}} \\ 3&=x \end{aligned}\)
Sustituto de espalda.
\(x+5=\color{OliveGreen}{3}\color{black}{+5=8}\)
\(x+5=\color{OliveGreen}{3}\color{black}{+7=10}\)
Respuesta:
Los tres lados del triángulo miden\(3\) pulgadas,\(8\) pulgadas y\(10\) pulgadas. El cheque se deja al lector.
Ejercicio\(\PageIndex{2}\)
La longitud de un rectángulo es\(1\) pie menos del doble de su ancho. Si el perímetro es\(46\) pies, encuentra las dimensiones.
- Contestar
-
Ancho:\(8\) pies; largo:\(15\) pies
Problemas que involucran dinero y porcentajes
Siempre que se establece una ecuación que involucra un porcentaje, generalmente necesitamos convertir el porcentaje a un decimal o fracción. Si la pregunta pide un porcentaje, entonces no olvides convertir tu respuesta a un porcentaje al final. Además, cuando se trata de dinero, asegúrese de redondear a dos decimales.
Ejemplo\(\PageIndex{10}\)
Si un par de zapatos cuesta $\(52.50\) incluyendo un\(7\frac{1}{4}\)% de impuesto, ¿cuál es el costo original del artículo antes de agregar impuestos?
Solución:
Comience por convertir\(7\frac{1}{4}\)% a decimal.
\(7\frac{1}{4}%=7.25%=0.0725\)
El monto del impuesto es esta tasa multiplicada por el costo original del artículo. El costo original del artículo es lo que se le pide que encuentre.
Dejar\(c\) representar el costo del artículo\(\underline{\text{before taxes}}\) se agregan.
\(\color{Cerulean}{amount\:of\:tax\:=\:tax\:rate\:\cdot\:cost\:of\:item}\)
\(=0.0725\cdot c\)
\(\color{Cerulean}{total\:cost\:=\:cost\:of\:item\:+\:amount\:of\:tax}\)
\(52.50=c+0.0725c\)
Utilice esta ecuación para resolver por\(c\), el costo original del artículo.
\(\begin{aligned} 52.50&=\color{OliveGreen}{1c+0.0725c} \\ 52.50&=1.0725c \\ \frac{52.50}{\color{Cerulean}{1.0725}}&=\frac{1.0725c}{\color{Cerulean}{1.0725}} \\ 48.95& \approx c \end{aligned}\)
Respuesta:
El costo del artículo antes de impuestos es de $\(48.95\). Verifique esto multiplicando $\(48.95\) por\(0.0725\) para obtener el impuesto y agréguelo a este costo.
Ejemplo\(\PageIndex{11}\)
Dada una tasa de interés anual\(5\frac{1}{8}\)%, ¿cuánto tiempo tardará $ en\(1,200\) producir $\(307.50\) en interés simple?
Solución:
Dejar\(t\) representar el tiempo necesario para ganar $\(307.50\) al\(5.125\)%.
Organizar los datos necesarios para utilizar la fórmula de interés simple\(I=prt\).
| Dados intereses para el periodo de tiempo: | \(I=\)$\(307.50\) |
| Dado principal: | \(p=\)$\(1200\) |
| Tasa dada: | \(r=5\frac{1}{8}\)%\(=5.125\)%\(=0.05125\) |
A continuación, sustituir todas las cantidades conocidas en la fórmula y luego resolver por el único desconocido,\(t\).
\(\begin{aligned} I&=prt \\ \color{OliveGreen}{307.50}&=\color{OliveGreen}{1200}\color{black}{(}\color{OliveGreen}{0.05125}\color{black}{)t} \\ 307.50&=61.5t \\ \frac{307.50}{\color{Cerulean}{61.5}}&=\frac{61.5t}{\color{Cerulean}{61.5}} \\ 5&=t \end{aligned}\)
Respuesta:
Se necesitan\(5\) años para $\(1,200\) invertido en\(5\frac{1}{8}\)% para ganar $\(307.50\) en interés simple.
Ejemplo\(\PageIndex{12}\)
Mary invirtió sus ahorros totales de $\(3,400\) en dos cuentas. Su cuenta de fondos mutuos ganó\(8\)% el año pasado y su CD obtuvo\(5\)%. Si su interés total para el año era $\(245\), ¿cuánto había en cada cuenta?
Solución:
La relación entre las dos incógnitas es que suman $3,400. Cuando se trata de un total, una técnica común utilizada para evitar dos variables es representar la segunda desconocida como la diferencia del total y la primera desconocida.
Dejar\(x\) representar el monto invertido en el fondo mutuo en\(8\)%\(=0.08\).
Dejar\(3,400-x\) representar la cantidad restante invertida en el CD en\(5\)%\(=0.05\).
El interés total es la suma de los intereses obtenidos de cada cuenta.
| Intereses devengados en el fondo mutuo: | \(I=Prt=x⋅0.08⋅1=0.08x\) |
| Intereses devengados en el CD: | \(I=Prt=(3,400−x)⋅0.05⋅1=0.05(3,400−x)\) |
\(\color{Cerulean}{mutual\:fund\:interest\:+\:CD\:interest\:=\:total\:interest}\)
\(0.08x+0.05(3,400-x)=245\)
Esta ecuación modela el problema con una variable. Resolver para\(x\).
\(\begin{aligned} 0.08x+0.05(3,400-x)&=245 \\ \color{OliveGreen}{0.08x}\color{black}{+170}\color{OliveGreen}{-0.05x}&=245 \\ 0.03x+170\color{Cerulean}{-170} &=245\color{Cerulean}{-170} \\ 0.03x&=75 \\ \frac{0.03x}{\color{Cerulean}{0.03}}&=\frac{75}{\color{Cerulean}{0.03}} \\ x&=2,500 \end{aligned}\)
Sustituto de espalda.
\(3,400-x=3,400-\color{OliveGreen}{2,500}\color{black}{=900}\)
Respuesta:
Mary invirtió $\(2,500\) a\(8\)% en un fondo mutuo y $\(900\) a\(5\)% en un CD.
Ejemplo\(\PageIndex{13}\)
Joe tiene un puñado de monedas de diez centavos y trimestres que valora $\(5.30\). Tiene uno menos del doble de diez minutos que cuartos. ¿Cuántas de cada moneda tiene?
Solución:
Comience por identificar las variables.
Vamos a\(q\) representar el número de cuartos que tiene Joe.
Dejar\(2q-1\) representar el número de dimes.
Para determinar el valor total de un número de monedas, multiplique el número de monedas por el valor de cada moneda. Por ejemplo, los\(5\) trimestres tienen un valor $\(0.25 ⋅ 5 =\) $\(1.25\).
\(\color{Cerulean}{value\:in\:quarters\:+\:value\:in\:dimes\:=\:total\:value\:of\:coins}\)
\(0.25q+0.10(2q-1)=5.30\)
Resolver por el número de trimestres,\(q\).
\(\begin{aligned} 0.25q+0.10(2q-1)&=5.30 \\ \color{OliveGreen}{0.25q+0.20q}\color{black}{-0.10}&=5.30 \\ 0.45q-0.10&=5.30 \\ 0.45q-0.10\color{Cerulean}{+0.10}&=5.30\color{Cerulean}{+0.10} \\ 0.45q&=5.40 \\ \frac{0.45q}{\color{Cerulean}{0.45}}&=\frac{5.40}{\color{Cerulean}{0.45}} \\ q&=12 \end{aligned}\)
Volver a sustituir en\(2q − 1\) para encontrar el número de monedas de diez centavos.
\(2q-1=2(\color{OliveGreen}{12}\color{black}{)-1=24-1=23}\)
Respuesta:
Joe tiene\(12\) cuartos y\(23\) diez mil dólares. Verifique multiplicando $\(0.25 ⋅ 12 = \) $\(3.00\) y $\(0.10 ⋅ 23 = \) $\(2.30\). Después agregue para obtener el monto correcto: $\(3.00 + \) $\(2.30 = \) $\(5.30\).
Ejercicio\(\PageIndex{3}\)
Se invierte un monto total\(5,900\) de $ en dos cuentas. Una cuenta gana\(3.5\)% de interés y otra gana\(4.5\)%. Si el interés por\(1\) año es $\(229.50\), entonces ¿cuánto se invierte en cada cuenta?
- Contestar
-
$\(3,600\) se invierte en\(3.5\)% y $\(2,300\) en\(4.5\)%.
Problemas de movimiento uniforme (problemas de distancia)
El movimiento uniforme se refiere al movimiento a una velocidad, o tasa que no cambia. Podemos determinar la distancia recorrida multiplicando la tasa promedio por el tiempo recorrido a ese ritmo con la fórmula\(D=r⋅t\). Las aplicaciones que involucran movimiento uniforme suelen tener muchos datos, por lo que ayuda a organizar primero los datos en un gráfico y luego configurar una ecuación algebraica que modela el problema.
Ejemplo\(\PageIndex{14}\)
Dos trenes salen de la estación al mismo tiempo viajando en direcciones opuestas. Uno viaja a\(70\) millas por hora y el otro a\(60\) millas por hora. ¿Cuánto tiempo tarda la distancia entre ellos en llegar a\(390\) millas?
Solución:
Primero, identificar la cantidad desconocida y organizar los datos.
Vamos a\(t\) representar el tiempo que se tarda en separar\(390\) millas.
.png)
Figura\(\PageIndex{6}\)
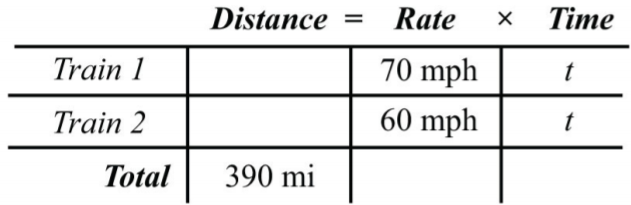
La información dada se rellena en la siguiente tabla. El tiempo para cada tren es igual.
.png)
Figura\(\PageIndex{7}\)
Para evitar introducir dos variables más, utilice la fórmula\(D=r⋅t\) para rellenar las distancias desconocidas recorridas por cada tren.
Distancia recorrida en tren 1:\(D=r\cdot t=70\cdot t\)
Distancia recorrida por tain 2:\(D=r\cdot t=60\cdot t\)
Ahora podemos rellenar completamente el gráfico.
.png)
Figura\(\PageIndex{8}\)
La configuración algebraica se define por la columna de distancia. El problema pregunta por el tiempo que tarda la distancia total en llegar a\(390\) millas.
.png)
Figura\(\PageIndex{9}\)
Resolver para\(t\).
\(\begin{aligned} 70t+60t&=390 \\ 130t&=390 \\ \frac{130t}{\color{Cerulean}{130}}&=\frac{390}{\color{Cerulean}{130}} \\ t&=3 \end{aligned}\)
Respuesta:
La distancia entre los trenes tarda\(3\) horas en llegar a\(390\) millas.
Ejemplo\(\PageIndex{15}\)
Un tren que viaja sin escalas a su destino es capaz de realizar el viaje a una velocidad promedio de\(72\) millas por hora. En el viaje de regreso, el tren hace varias paradas y sólo es capaz de promediar\(48\) millas por hora. Si el viaje de regreso tarda\(2\) horas más que el viaje inicial al destino, entonces ¿cuál es el tiempo de viaje en cada sentido?
Solución:
Primero, identificar la cantidad desconocida y organizar los datos.
Dejar\(t\) representar el tiempo que se tarda en llegar al destino.
Dejar\(t+2\) representar el tiempo que toma para el viaje de regreso.
.png)
Figura\(\PageIndex{10}\)
La información dada se rellena en la siguiente tabla:
.png)
Figura\(\PageIndex{11}\)
Usa la fórmula\(D=r⋅t\) para rellenar las distancias desconocidas.
Distancia recorrida en el destino:\(D=r\cdot t=72\cdot t\)
Distancia recorrida en el viaje de regreso:\(D=r\cdot t=48\cdot (t+2)\)
Utilice estas expresiones para completar el gráfico.
.png)
Figura\(\PageIndex{12}\)
La configuración algebraica se define de nuevo por la columna de distancia. En este caso, la distancia al destino y regreso es la misma, y la ecuación es
\(72t=48(t+2)\)
Resolver para\(t\).
\(\begin{aligned} 72t&=48(t+2) \\ 722&=48t+96 \\ 72t-48t&=48t+96-48t \\ 24t&=96 \\ \frac{24t}{24}&=\frac{96}{24} \\ t&=4 \end{aligned}\)
El viaje de regreso toma\(t+2=4+2=6\) horas.
Respuesta:
Se necesitan\(4\) horas para llegar al destino y\(6\) horas para regresar.
Ejercicio\(\PageIndex{4}\)
Mary sale a la escuela en bicicleta a una tasa promedio de\(6\) millas por hora. Su hermana Kate, llegando tarde, se va\(15\) minutos después y pedalea al doble de esa velocidad. ¿Cuánto tardará Kate en ponerse al día con Mary? ¡Ten cuidado! Preste atención a las unidades dadas en el problema.
- Contestar
-
Kate tarda\(15\) minutos en ponerse al día.
Claves para llevar
- Simplificar el proceso de resolución de problemas del mundo real mediante la creación de modelos matemáticos que describen la relación entre incógnitas. Usa álgebra para resolver las ecuaciones resultantes.
- Adivinar y verificar soluciones es una mala práctica. Esta técnica a veces puede producir respuestas correctas, pero no es confiable, especialmente cuando los problemas se vuelven más complejos.
- Lee el problema varias veces y busca las palabras y frases clave. Identificar las incógnitas y asignar variables o expresiones a las cantidades desconocidas. Busca relaciones que te permitan usar solo una variable. Establecer un modelo matemático para la situación y utilizar álgebra para resolver la ecuación. Verifique si la solución tiene sentido y presente la solución en forma de oración.
- No evites problemas de palabras: resolverlos puede ser divertido y gratificante. Con mucha práctica encontrarás que realmente no son tan malos después de todo. Modelar y resolver aplicaciones es una de las principales razones para estudiar álgebra.
- No se sienta desanimado cuando el primer intento de resolver un problema de palabras no funciona. Esto es parte del proceso. Prueba algo diferente y aprende de intentos incorrectos.
Ejercicio\(\PageIndex{5}\) Translate
Traducir lo siguiente en ecuaciones algebraicas.
- La suma de un número y\(6\) es\(37\).
- Cuando\(12\) se resta del doble de algún número el resultado es\(6\).
- Catorce\(5\) veces menos de lo que es un número\(1\).
- Dos veces se resta algún número\(30\) y el resultado es\(50\).
- Cinco veces la suma de\(6\) y algún número es\(20\).
- La suma de\(5\) veces algún número y\(6\) es\(20\).
- Cuando la suma de un número y\(3\) se resta\(10\) del resultado es\(5\).
- La suma de tres veces un número y cinco veces ese mismo número es\(24\).
- Diez se resta del doble de algún número y el resultado es la suma del número y\(2\).
- Seis menos que algún número es diez veces la suma de ese número y\(5\).
- Contestar
-
1. \(x+6=37\)
3. \(5x−14=1\)
5. \(5(x+6)=20\)
7. \(10−(x+3)=5\)
9. \(2x−10=x+2\)
Ejercicio\(\PageIndex{6}\) Number Problems
Establecer una ecuación algebraica y luego resolver.
- Un entero mayor es\(1\) más de dos veces otro entero. Si la suma de los enteros es\(25\), busque los enteros.
- Si un entero mayor es\(2\) más que\(4\) veces otro entero y su diferencia es\(32\), busque los enteros.
- Un entero es\(30\) más que otro entero. Si la diferencia entre el mayor y el doble el menor es\(8\), encuentra los enteros.
- El cociente de algún número y\(4\) es\(22\). Encuentra el número.
- Ocho veces un número se disminuye tres veces el mismo número, dando una diferencia de\(20\). ¿Cuál es el número?
- Un entero es dos unidades menos que otro. Si su suma es\(−22\), encuentra los dos enteros.
- La suma de dos enteros consecutivos es\(139\). Encuentra los enteros.
- La suma de tres enteros consecutivos es\(63\). Encuentra los enteros.
- La suma de tres enteros consecutivos es\(279\). Encuentra los enteros.
- La diferencia de dos veces el menor de dos enteros consecutivos y el mayor es\(39\). Encuentra los enteros.
- Si el menor de dos enteros consecutivos se resta de dos veces el mayor, entonces el resultado es\(17\). Encuentra los enteros.
- La suma de dos enteros pares consecutivos es\(46\). Encuentra los enteros.
- La suma de dos enteros pares consecutivos es\(238\). Encuentra los enteros.
- La suma de tres enteros pares consecutivos es\(96\). Encuentra los enteros.
- Si el menor de dos enteros pares consecutivos se resta de\(3\) veces mayor es el resultado\(42\). Encuentra los enteros.
- La suma de tres enteros pares consecutivos es\(90\). Encuentra los enteros.
- La suma de dos enteros impares consecutivos es\(68\). Encuentra los enteros.
- La suma de dos enteros impares consecutivos es\(180\). Encuentra los enteros.
- La suma de tres enteros impares consecutivos es\(57\). Encuentra los enteros.
- Si el menor de dos enteros impares consecutivos se resta del doble de mayor es el resultado\(23\). Encuentra los enteros.
- Dos veces la suma de dos enteros impares consecutivos es\(32\). Encuentra los enteros.
- La diferencia entre dos veces el mayor de dos enteros impares consecutivos y el menor es\(59\). Encuentra los enteros.
- Contestar
-
1. \(8, 17\)
3. \(22, 52\)
5. \(4\)
7. \(69, 70\)
9. \(92, 93, 94\)
11. \(15, 16\)
13. \(118, 120\)
15. \(18, 20\)
17. \(33, 35\)
19. \(17, 19, 21\)
21. \(7, 9\)
Ejercicio\(\PageIndex{7}\) Geometry Problems
Establecer una ecuación algebraica y luego resolver.
- Si el perímetro de un cuadrado es de\(48\) pulgadas, entonces encuentra la longitud de cada lado.
- La longitud de un rectángulo es\(2\) pulgadas más larga que su ancho. Si el perímetro es\(36\) pulgadas, encuentra el largo y ancho.
- La longitud de un rectángulo es\(2\) pies menos del doble de su ancho. Si el perímetro es\(26\) pies, encuentra el largo y ancho.
- El ancho de un rectángulo es\(2\) centímetros menos de la mitad de su longitud. Si el perímetro es de\(56\) centímetros, encuentra el largo y ancho.
- La longitud de un rectángulo es\(3\) pies menos del doble de su ancho. Si el perímetro es\(54\) pies, encuentra las dimensiones del rectángulo.
- Si la longitud de un rectángulo es el doble de largo que el ancho y su perímetro mide\(72\) pulgadas, encuentra las dimensiones del rectángulo.
- El perímetro de un triángulo equilátero mide\(63\) centímetros. Encuentra la longitud de cada lado.
- Un triángulo isósceles cuya base es la mitad de largo que los otros dos lados iguales tiene un perímetro de\(25\) centímetros. Encuentra la longitud de cada lado.
- Cada una de las dos patas iguales de un triángulo isósceles tiene el doble de longitud de la base. Si el perímetro es de\(105\) centímetros, entonces ¿cuánto dura cada pata?
- Un triángulo tiene lados cuyas medidas son números enteros pares consecutivos. Si el perímetro es\(42\) pulgadas, encuentra la medida de cada lado.
- Un triángulo tiene lados cuyas medidas son números enteros impares consecutivos. Si el perímetro es\(21\) pulgadas, encuentra la medida de cada lado.
- Un triángulo tiene lados cuyas medidas son números enteros consecutivos. Si el perímetro es\(102\) pulgadas, entonces encuentra la medida de cada lado.
- La circunferencia de un círculo mide\(50π\) unidades. Encuentra el radio.
- La circunferencia de un círculo mide\(10π\) unidades. Encuentra el radio.
- La circunferencia de un círculo mide\(100\) centímetros. Determinar el radio a la décima más cercana.
- La circunferencia de un círculo mide\(20\) centímetros. Encuentra el diámetro redondeado a la centésima más cercana.
- El diámetro de un círculo mide\(5\) pulgadas. Determinar la circunferencia a la décima más cercana.
- El diámetro de un círculo es\(13\) pies. Calcular el valor exacto de la circunferencia.
- Contestar
-
1. \(12\)pulgadas
3. Ancho:\(5\) pies; largo:\(8\) pies
5. Ancho:\(10\) pies; largo:\(17\) pies
7. \(21\)centímetros
9. \(21\)centímetros,\(42\) centímetros,\(42\) centímetros
11. \(5\)pulgadas,\(7\) pulgadas,\(9\) pulgadas
13. \(25\)unidades
15. \(15.9\)centímetros
17. \(15.7\)pulgadas
Ejercicio\(\PageIndex{8}\) Percent and Money Problems
Establecer una ecuación algebraica y luego resolver.
- Calcular el interés simple ganado por una inversión\(2\) -año de $\(1,550\) a una tasa de interés\(8\frac{3}{4}\)% anual.
- Calcular el interés simple ganado por una inversión\(1\) -año de $\(500\) a una tasa de interés\(6\)% anual.
- ¿Por cuántos años\(10,000\) se deben invertir $ a una tasa de interés\(8\frac{1}{2}\)% anual para producir $\(4,250\) en interés simple?
- ¿Por cuántos años\(1,000\) se deben invertir $ a una tasa de interés\(7.75\)% anual para producir $\(503.75\) en interés simple?
- ¿A qué tasa de interés anual\(2,500\) se debe invertir $ durante\(3\) años para arrojar $\(412.50\) en interés simple?
- ¿A qué tasa de interés anual\(500\) se debe invertir $ durante\(2\) años para arrojar $\(93.50\) en interés simple?
- Si el interés simple ganado por\(1\) año era $\(47.25\) y la tasa anual era\(6.3\)%, ¿cuál era el principal?
- Si el interés simple ganado por\(2\) años era $\(369.60\) y la tasa anual era\(5\frac{1}{4}\)%, ¿cuál era el principal?
- Joe invirtió la declaración de\(2,500\) impuestos $ del año pasado en dos cuentas diferentes. Puso la mayor parte del dinero en una cuenta del mercado monetario ganando\(5\)% interés simple. Invirtió el resto en un CD ganando\(8\)% interés simple. ¿Cuánto puso en cada cuenta si el interés total del año era de $\(138.50\)?
- James invirtió $\(1,600\) en dos cuentas. Una cuenta gana\(4.25\)% interés simple y la otra gana\(8.5\)%. Si el interés tras\(1\) año era de $\(85\), ¿cuánto invirtió en cada cuenta?
- Jane tiene sus\(5,400\) ahorros de $ invertidos en dos cuentas. Ella tiene parte de ello en un CD con\(3\)% de interés anual y el resto en una cuenta de ahorro que gana\(2\)% de interés anual. Si el simple interés ganado de ambas cuentas es $\(140\) para el año, entonces ¿cuánto tiene en cada cuenta?
- Marty puso el aguinaldo de $ del año pasado\(2,400\) en dos cuentas. Invirtió parte en un CD con\(2.5\)% de interés anual y el resto en un fondo del mercado monetario con\(1.3\)% de interés anual. Su interés total para el año fue de $\(42.00\). ¿Cuánto invirtió en cada cuenta?
- Alice pone el dinero en dos cuentas, una con\(2\)% de interés anual y otra con\(3\)% de interés anual. Ella invierte tanto\(3\) tiempo en la cuenta de mayor rendimiento como en la cuenta de menor rendimiento. Si su interés total para el año es $\(27.50\), ¿cuánto invirtió en cada cuenta?
- Jim invirtió una herencia en dos bancos separados. Un banco ofreció\(5.5\)% de tasa de interés anual y el otro\(6\frac{1}{4}\)%. Invirtió el doble en la cuenta bancaria de mayor rendimiento que en la otra. Si su interés simple total por\(1\) año era $\(4,860\), entonces ¿cuál era el monto de su herencia?
- Si se anuncia un artículo a un costo de $\(29.99\) más\(9.25\)% de impuestos, ¿cuál es el costo total?
- Si se anuncia un artículo a un costo de $\(32.98\) más\(8\frac{3}{4}\)% de impuestos, ¿cuál es el costo total?
- Un artículo, incluyendo un\(8.75\)% de impuestos, cuesta $\(46.49\). ¿Cuál es el costo original antes de impuestos del artículo?
- Un artículo, incluyendo un\(5.48\)% de impuestos, cuesta $\(17.82\). ¿Cuál es el costo original antes de impuestos del artículo?
- Si una comida cuesta $\(32.75\), ¿cuál es el total después de agregar un\(15\)% de propina?
- ¿Cuánto cuesta un\(15\)% de propina en una factura de restaurante que totaliza $\(33.33\)?
- Ray tiene un puñado de monedas de diez y cinco centavos valorando $\(3.05\). Tiene\(5\) más dimes que cinco. ¿Cuántas de cada moneda tiene?
- Jill tiene\(3\) menos medio dólares que trimestres. El valor\(27\) de todas sus monedas se suma a $\(9.75\). ¿Cuántas de cada moneda tiene Jill?
- Cathy tiene que depositar $\(410\) por valor de billetes de cinco y diez dólares. Tiene\(1\) menos de tres veces más decenas que billetes de cinco dólares. ¿Cuántos de cada factura tiene que depositar?
- Billy tiene un montón de cuartos, diez centavos y cinco centavos que valora $\(3.75\). Tiene\(3\) más monedas de diez centavos que cuartos y\(5\) más monedas de cinco centavos que cuartos. ¿Cuántas de cada moneda tiene Billy?
- Mary tiene un frasco con billetes de un dólar, monedas de medio dólar y cuartos que valoran $\(14.00\). Tiene el doble de cuartos que monedas de medio dólar y la misma cantidad de monedas de medio dólar que los billetes de un dólar. ¿Cuántos de cada uno tiene?
- Chad tiene un bill-fold de billetes de uno, cinco y diez dólares por un total de $\(118\). Tiene\(2\) más de\(3\) veces tantos como billetes de cinco dólares y\(1\) menos billetes de diez que cinco dólares. ¿Cuántos de cada factura tiene Chad?
- Contestar
-
1. $\(271.25\)
3. \(5\)años
5. \(5.5\)%
7. $\(750.00\)
9. Joe invirtió $\(2,050\) en la cuenta del mercado monetario y $\(450\) en el CD.
11. Jane tiene $\(3,200\) en el CD y $\(2,200\) en ahorros.
13. Alice invirtió $\(250\) al\(2\)% y $\(750\) a un\(3\)%.
15. $\(32.76\)
17. $\(42.75\)
19. $\(37.66\)
21. Tiene\(17\) cinco y diez\(22\) mil dólares.
23. Cathy tiene billetes\(12\) de cinco y\(35\) diez dólares.
25. Mary tiene\(7\) billetes de un dólar, monedas de\(7\) medio dólar y\(14\) trimestres.
Ejercicio\(\PageIndex{9}\) Uniform Motion (Distance Problems)
Configure una ecuación algebraica luego resuelva.
- Dos autos salen de un lugar viajando en direcciones opuestas. Si un automóvil promedia\(55\) millas por hora y el otro promedia\(65\) millas por hora, entonces, ¿cuánto tiempo tardará en separar una distancia de\(300\) millas?
- Dos aviones salen del aeropuerto al mismo tiempo viajando en direcciones opuestas. Las velocidades promedio para los aviones son\(450\) millas por hora y\(395\) millas por hora. ¿Cuánto tardarán los aviones en estar a una distancia de\(1,478.75\) millas de distancia?
- Bill y Ted están corriendo por todo el país. Bill sale\(1\) hora antes que Ted y viaja a una tasa promedio de\(60\) millas por hora. Si Ted tiene la intención de ponerse al día a razón de\(70\) millas por hora, entonces ¿cuánto tiempo tomará?
- Dos hermanos salen del mismo lugar, uno en un automóvil y otro en bicicleta, para reunirse en casa de su abuela para cenar. Si un hermano promedia\(30\) millas por hora en el automóvil y el otro promedia\(12\) millas por hora en la bicicleta, entonces le toma al hermano en la bicicleta\(1\) una hora menos que\(3\) veces más larga que el otro en el automóvil. ¿Cuánto tarda cada uno de ellos en hacer el viaje?
- Un piloto de aerolínea comercial voló a una velocidad promedio de\(350\) millas por hora antes de ser informado de que su aeródromo de destino puede estar cerrado debido a las malas condiciones climáticas. En un intento de llegar antes de la tormenta, aumentó su velocidad\(400\) millas por hora y voló durante otras\(3\) horas. Si la distancia total volada era de\(2,950\) millas, entonces, ¿cuánto tardó el viaje?
- Dos hermanos condujeron los\(2,793\) kilómetros de Los Ángeles a Nueva York. Uno de los hermanos, manejando durante el día, pudo promediar\(70\) millas por hora, y el otro, manejando de noche, pudo promediar\(53\) millas por hora. Si el hermano que conducía de noche manejaba\(3\) horas menos que el hermano que conducía en el día, entonces, ¿cuántas horas manejaban cada uno?
- Joe y Ellen viven\(21\) a kilómetros de distancia. Partiendo al mismo tiempo, circulan el uno hacia el otro. Si Joe promedia\(8\) millas por hora y Ellen promedia\(6\) millas por hora, ¿cuánto tiempo les tomará reunirse?
- Si se tarda\(6\) minutos en conducir hasta el taller de reparación de automóviles a una velocidad promedio de\(30\) millas por hora, entonces ¿cuánto tiempo tomará caminar de regreso a una tasa promedio de\(4\) millas por hora?
- Jaime y Alex salen del mismo lugar y viajan en direcciones opuestas. Las condiciones de tránsito permitieron a Alex promediar\(14\) millas por hora más rápido que Jaime. Después de\(1\frac{1}{2}\) horas están\(159\) a kilómetros de distancia. Encuentra la velocidad a la que cada uno pudo viajar.
- Jane y Holly viven\(51\) a kilómetros de distancia y se van al mismo tiempo viajando una hacia la otra para reunirse para almorzar. Jane viajó por la autopista al doble de la velocidad promedio que Holly. Pudieron reunirse en media hora. ¿A qué ritmo viajó cada uno?
- Contestar
-
1. \(2.5\)horas
3. \(6\)horas
5. \(8\)horas
7. \(1\frac{1}{2}\)horas
9. Jaime:\(46\) millas por hora; Alex:\(60\) millas por hora
Ejercicio\(\PageIndex{10}\) Discussion Board Topics
- Discutir ideas para calcular impuestos y propinas mentalmente.
- Investigar métodos históricos para representar incógnitas.
- Investigar y comparar interés simple e interés compuesto. ¿Cuál es la diferencia?
- Discutir por qué el álgebra es un tema obligatorio.
- Investigar formas de demostrar que un decimal repetido es racional. Comparta sus hallazgos en el panel de discusión.
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar
5. Las respuestas pueden variar


