5.3: Sumando y restando expresiones radicales

Objetivos de aprendizaje

• Sumar y restar como radicales.
• Simplifica las expresiones radicales que involucran radicales similares.

Sumando y restando radicales similares

Sumar y restar expresiones radicales es similar a sumar y restar términos similares. Se considera que los radicales son como los radicales ¹⁶, o radicales similares ¹⁷, cuando comparten el mismo índice y radicando. Por ejemplo, los términos\(2\sqrt{6}\) y\(5\sqrt{6}\) contienen radicales similares y se pueden agregar usando la propiedad distributiva de la siguiente manera:

\(\begin{aligned} 2 \sqrt { 6 } + 5 \sqrt { 6 } & = ( 2 + 5 ) \sqrt { 6 } \\ & = 7 \sqrt { 6 } \end{aligned}\)

Normalmente, no mostramos el paso que involucra la propiedad distributiva y simplemente escribimos,

\(2 \sqrt { 6 } + 5 \sqrt { 6 } = 7 \sqrt { 6 }\)

Al agregar términos con radicales similares, agregue solo los coeficientes; la parte radical sigue siendo la misma.

Ejemplo\(\PageIndex{1}\):

Agregar:\(7 \sqrt [ 3 ] { 5 } + 3 \sqrt [ 3 ] { 5 }\).

Solución

Los términos son como radicales; por lo tanto, sumar los coeficientes.

\(7 \sqrt [ 3 ] { 5 } + 3 \sqrt [ 3 ] { 5 } = 10 \sqrt [ 3 ] { 5 }\)

Respuesta:

\(10 \sqrt [ 3 ] { 5 }\)

La resta se realiza de manera similar.

Ejemplo\(\PageIndex{2}\):

Restar:\(4 \sqrt { 10 } - 5 \sqrt { 10 }\).

Solución

\(\begin{aligned} 4 \sqrt { 10 } - 5 \sqrt { 10 } & = ( 4 - 5 ) \sqrt { 10 } \\ & = - 1 \sqrt { 10 } \\ & = - \sqrt { 10 } \end{aligned}\)

Respuesta:

\(- \sqrt { 10 }\)

Si el radicando y el índice no son exactamente los mismos, entonces los radicales no son similares y no podemos combinarlos.

Ejemplo\(\PageIndex{3}\):

Simplificar:\(10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 }\).

Solución

\(\begin{aligned} 10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 } & = \color{Cerulean}{10 \sqrt { 5 } - 9 \sqrt { 5 }}\color{black}{ +}\color{OliveGreen}{ 6 \sqrt { 2 } - 7 \sqrt { 2 }} \\ & = \sqrt { 5 } - \sqrt { 2 } \end{aligned}\)

No podemos simplificar más porque\(\sqrt{5}\) y no\(\sqrt{2}\) somos como radicales; los radicandos no son lo mismo.

Respuesta:

\(\sqrt { 5 } - \sqrt { 2 }\)

\(\color{YellowOrange}{\text{Caution:}}\)Es importante señalar eso\(\sqrt { 5 } - \sqrt { 2 } \neq \sqrt { 5 - 2 }\). Podemos verificar esto calculando el valor de cada lado con una calculadora.

\(\begin{array} { c } { \sqrt { 5 } - \sqrt { 2 } \approx 0.82 } \\ { \sqrt { 5 - 2 } = \sqrt { 3 } \approx 1.73 } \end{array}\)

En general, tenga en cuenta eso\(\sqrt [ n ] { a } \pm \sqrt [ n ] { b } \neq \sqrt [ n ] { a \pm b }\).

Ejemplo\(\PageIndex{4}\):

Simplificar:\(5 \sqrt [ 3 ] { 10 } + 3 \sqrt { 10 } - \sqrt [ 3 ] { 10 } - 2 \sqrt { 10 }\).

Solución

\(\begin{aligned} 5 \sqrt [ 3 ] { 10 } + 3 \sqrt { 10 } - \sqrt [ 3 ] { 10 } - 2 \sqrt { 10 } & =\color{Cerulean}{ 5 \sqrt [ 3 ] { 10 } - \sqrt [ 3 ] { 10 }}\color{black}{ +}\color{OliveGreen}{ 3 \sqrt { 10 } - 2 \sqrt { 10 }} \\ & = 4 \sqrt [ 3 ] { 10 } + \sqrt { 10 } \end{aligned}\)

No podemos simplificar más, porque\(\sqrt [ 3 ] { 10 }\) y no\(\sqrt { 10 }\) son como radicales; los índices no son los mismos.

Respuesta:

\(4 \sqrt [ 3 ] { 10 } + \sqrt { 10 }\)

Sumando y restando expresiones radicales

A menudo, tendremos que simplificar antes de poder identificar los radicales similares dentro de los términos.

Ejemplo\(\PageIndex{5}\):

Restar:\(\sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 }\).

Solución

A primera vista, los radicales no parecen ser similares. No obstante, después de simplificar por completo, veremos que podemos combinarlos.

\(\begin{aligned} \sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 } & = \sqrt { 16 } \cdot 2 - \sqrt { 9 \cdot 2 } + \sqrt { 25 \cdot 2 } \\ & = 4 \sqrt { 2 } - 3 \sqrt { 2 } + 5 \sqrt { 2 } \\ & = 6 \sqrt { 2 } \end{aligned}\)

Respuesta:

\(6\sqrt{2}\)

Ejemplo\(\PageIndex{6}\):

Simplificar:\(\sqrt [ 3 ] { 108 } + \sqrt [ 3 ] { 24 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 81 }\).

Solución:

Comience por buscar factores de cubo perfectos de cada radicando.

\(\begin{aligned} \sqrt [ 3 ] { 108 } + \sqrt [ 3 ] { 24 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 81 } & = \sqrt [ 3 ] { 27 \cdot 4 } + \sqrt [ 3 ] { 8 \cdot 3 } - \sqrt [ 3 ] { 8 \cdot 4 } - \sqrt [ 3 ] { 27 \cdot 3 }\quad\color{Cerulean}{Simplify.} \\ & = 3 \sqrt [ 3 ] { 4 } + \color{Cerulean}{2 \sqrt [ 3 ] { 3 } }\color{black}{-} 2 \sqrt [ 3 ] { 4 } - \color{Cerulean}{3 \sqrt [ 3 ] { 3 }} \quad\quad\quad\quad\quad\color{Cerulean}{Combine\:like\:terms.} \\ & = \sqrt [ 3 ] { 4 } - \sqrt [ 3 ] { 3 } \end{aligned}\)

Respuesta:

\(\sqrt [ 3 ] { 4 } - \sqrt [ 3 ] { 3 }\)

Ejercicio\(\PageIndex{1}\)

Simplificar:\(\sqrt { 20 } + \sqrt { 27 } - 3 \sqrt { 5 } - 2 \sqrt { 12 }\).

Responder

\(- \sqrt { 5 } - \sqrt { 3 }\)

www.youtube.com/v/qtapdvyBp1G

A continuación, se trabaja con expresiones radicales que involucran variables. En esta sección, supongamos que todos los radicandos que contienen expresiones variables no son negativos.

Ejemplo\(\PageIndex{7}\):

Simplificar:\(- 9 \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } + 10 \sqrt [ 3 ] { 5 x }\).

Solución

Combina como radicales.

\(\begin{aligned} - 9 \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } + 10 \sqrt [ 3 ] { 5 x } & = \color{Cerulean}{- 9 \sqrt [ 3 ] { 5 x } + 10 \sqrt [ 3 ] { 5 x } }\color{black}{-}\color{OliveGreen}{ \sqrt [ 3 ] { 2 x }} \\ & = \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } \end{aligned}\)

No podemos combinar más porque las expresiones radicales restantes no comparten el mismo radicando; no son como radicales. Nota:\(\sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } \neq \sqrt [ 3 ] { 5 x - 2 x }\).

Respuesta:

\(\sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x }\)

A menudo encontraremos la necesidad de restar una expresión radical con múltiples términos. Si este es el caso, recuerde aplicar la propiedad distributiva antes de combinar términos similares.

Ejemplo\(\PageIndex{8}\):

Simplificar:\(( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } )\).

Solución

\(\begin{aligned} ( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } ) & = 5 \sqrt { x } - 4 \sqrt { y } - 4 \sqrt { x } + 7 \sqrt { y } \quad\color{Cerulean}{Distribute.} \\ & = 5 \sqrt { x } - 4 \sqrt { x } - 4 \sqrt { y } + 7 \sqrt { y } \\ & = \sqrt { x } + 3 \sqrt { y } \end{aligned}\)

Respuesta:

\(\sqrt { x } + 3 \sqrt { y }\)

Hasta que no simplifiquemos, a menudo no está claro qué términos que involucran radicales son similares. Los pasos generales para simplificar las expresiones radicales se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{9}\):

Simplificar:\(5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - \left( x \sqrt [ 3 ] { 24 x } + 4 \sqrt [ 3 ] { 3 x ^ { 3 } } \right)\).

Solución

Paso 1: Simplificar la expresión radical. En este caso, distribuir y luego simplificar cada término que involucre a un radical.

\(\begin{array} { l } { 5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - \left( x \sqrt [ 3 ] { 24 x } + 4 \sqrt [ 3 ] { 3 x ^ { 3 } } \right) } \\ { = 5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - x \sqrt[3] { 24 x } - 4 \sqrt [ 3 ] { 3 x ^ { 3 } } } \\ { = 5 \sqrt [ 3 ] { 3 \cdot x \cdot x ^ { 3 } } + \sqrt [ 3 ] { 8 \cdot 3 \cdot x ^ { 3 } } - x \sqrt [ 3 ] { 8 \cdot 3 x } - 4 \sqrt [ 3 ] { 3 x ^ { 3 } } } \\ { = 5 x \sqrt [ 3 ] { 3 x } + 2 x \sqrt [ 3 ] { 3 } - 2 x \sqrt [ 3 ] { 3 x } - 4 x \sqrt [ 3 ] { 3 } } \end{array}\)

Paso 2: Combina todos como radicales. Recuerde agregar solo los coeficientes; las partes variables siguen siendo las mismas.

\(\begin{array} { l } { =\color{Cerulean}{ 5 x \sqrt [ 3 ] { 3 x } }\color{OliveGreen}{+ 2 x \sqrt [ 3 ] { 3 }}\color{Cerulean}{ - 2 x \sqrt [ 3 ] { 3 x } }\color{OliveGreen}{- 4 x \sqrt [ 3 ] { 3 } } }\\ { = 3 x \sqrt [ 3 ] { 3 x } - 2 x \sqrt [ 3 ] { 3 } } \end{array}\)

Respuesta:\(3 x \sqrt [ 3 ] { 3 x } - 2 x \sqrt [ 3 ] { 3 }\)

Ejemplo\(\PageIndex{10}\):

Simplificar:\(2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b }\).

Solución

\(\begin{array} { l } { 2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b } } \\ { = 2 a \sqrt { 25 \cdot 5 \cdot a ^ { 2 } \cdot b } - a ^ { 2 } \sqrt { 16 \cdot 5 \cdot b } + 4 \sqrt { 4 \cdot 5 \cdot \left( a ^ { 2 } \right) ^ { 2 } b } }\quad\color{Cerulean}{Factor.} \\ { = 2 a \cdot 5 \cdot a \sqrt { 5 b } - a ^ { 2 } \cdot 4 \sqrt { 5 b } + 4 \cdot 2 \cdot a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\:\color{Cerulean}{Simplify.} \\ { = 10 a ^ { 2 } \sqrt { 5 b } - 4 a ^ { 2 } \sqrt { 5 b } + 8 a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\color{Cerulean}{Combine\:like\:terms.} \\ { = 14 a ^ { 2 } \sqrt { 5 b } } \end{array}\)

Respuesta:

\(14 a ^ { 2 } \sqrt { 5 b }\)

Ejercicio\(\PageIndex{2}\)

\(\sqrt [ 3 ] { 2 x ^ { 6 } y } + \sqrt [ 3 ] { x y ^ { 3 } } - \left( y \sqrt [ 3 ] { 27 x } - 2 x \sqrt [ 3 ] { 2 x ^ { 3 } y } \right)\)

Responder

\(3 x ^ { 2 } \sqrt [ 3 ] { 2 y } - 2 y \sqrt [ 3 ] { x }\)

www.youtube.com/v/oyeyj7ubc-q

nota

Toma nota cuidadosa de las diferencias entre productos y sumas dentro de un radical. Asumir ambos\(x\) y no\(y\) son negativos.

\(\begin{array} { l } Products \quad \quad\quad\quad Sums\\\hline { \sqrt { x ^ { 2 } y ^ { 2 } } = x y \quad\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y } \\ { \sqrt [ 3 ] { x ^ { 3 } y ^ { 3 } } = x y } \quad\sqrt[3]{x^{3}+y^{3}} \neq x+ y \end{array}\)

El inmueble\(\sqrt [ n ] { a \cdot b } = \sqrt [ n ] { a } \cdot \sqrt [ n ] { b }\) dice que podemos simplificar los radicales cuando la operación en el radicando es multiplicación. No hay propiedad correspondiente para adición.

Ejemplo\(\PageIndex{11}\):

Calcular el perímetro del triángulo formado por los puntos\((-2,-1), (-3,6)\), y\((2,1)\).

Solución

La fórmula para el perímetro de un triángulo es\(P = a + b + c\) donde\(a, b\), y\(c\) representan las longitudes de cada lado. Trazando los puntos que tenemos,

Figura\(\PageIndex{1}\)

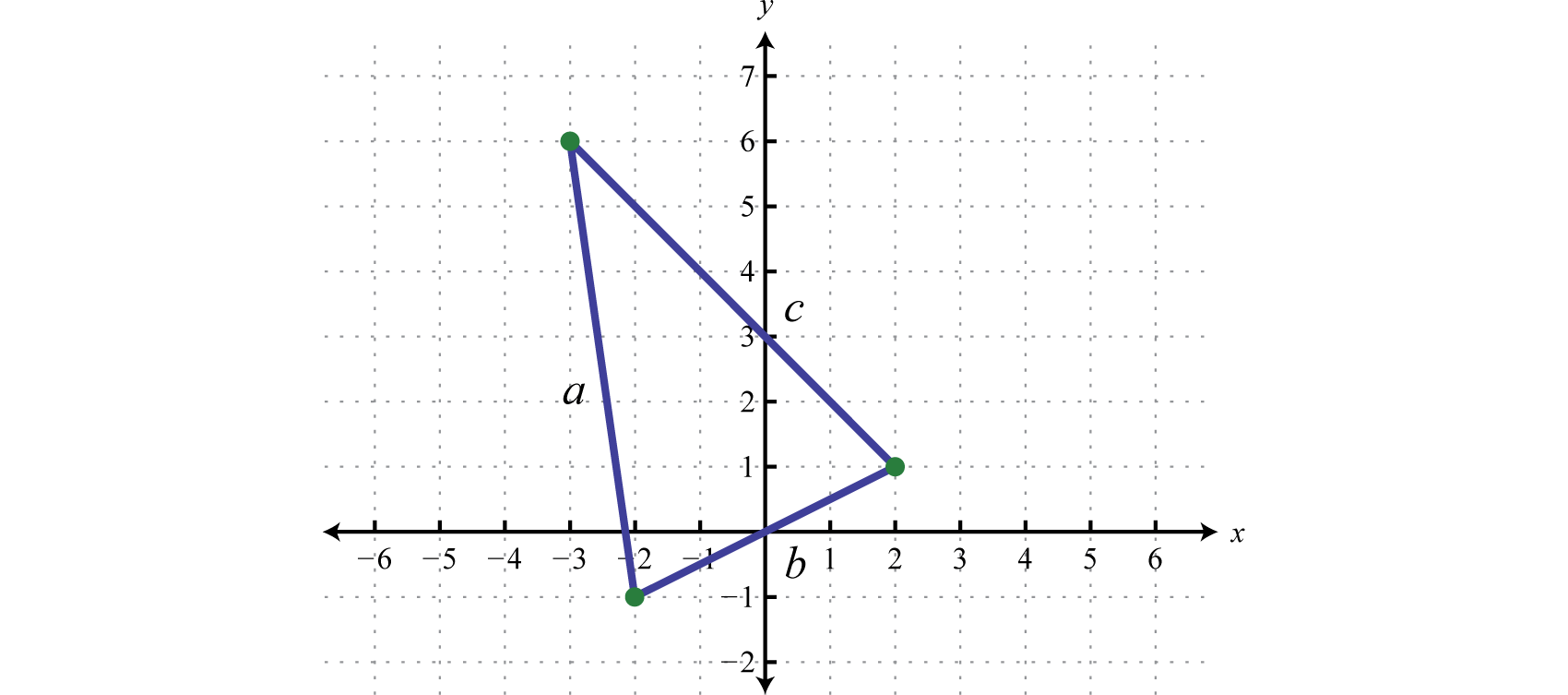
Usa la fórmula de distancia para calcular la longitud de cada lado.

\(\begin{aligned} a & = \sqrt { [ - 3 - ( - 2 ) ] ^ { 2 } + [ 6 - ( - 1 ) ] ^ { 2 } } &b&= \sqrt{[2-(-2)]^{2} + [1-(-1)]^{2}} \\ & = \sqrt { ( - 3 + 2 ) ^ { 2 } + ( 6 + 1 ) ^ { 2 } } &&= \sqrt{(2+2)^{2} + (1+1)^{2}} \\ & = \sqrt { ( - 1 ) ^ { 2 } + ( 7 ) ^ { 2 } } &&=\sqrt{(4)^{2}+(2)^{2}} \\ & = \sqrt { 1 + 49 }&&= \sqrt{16+4} \\ & = \sqrt { 50 } && =\sqrt{20}\\ & = 5 \sqrt { 2 } &&= 2\sqrt{5} \end{aligned}\)

De igual manera podemos calcular la distancia entre\((−3, 6)\) y\((2,1)\) y encontrar esas\(c = 5\sqrt{2}\) unidades. Por lo tanto, podemos calcular el perímetro de la siguiente manera:

\(\begin{aligned} P & = a + b + c \\ & = 5 \sqrt { 2 } + 2 \sqrt { 5 } + 5 \sqrt { 2 } \\ & = 10 \sqrt { 2 } + 2 \sqrt { 5 } \end{aligned}\)

Respuesta:

\(10 \sqrt { 2 } + 2 \sqrt { 5 }\)unidades

Claves para llevar

• Sumar y restar términos que contengan radicales similares al igual que a usted le gustan los términos. Si el índice y el radicando son exactamente los mismos, entonces los radicales son similares y se pueden combinar. Esto implica sumar o restar sólo los coeficientes; la parte radical sigue siendo la misma.
• Simplifica cada radical completamente antes de combinar términos similares.

Ejercicio\(\PageIndex{3}\)

Simplificar

1. \(10 \sqrt { 3 } - 5 \sqrt { 3 }\)
2. \(15 \sqrt { 6 } - 8 \sqrt { 6 }\)
3. \(9 \sqrt { 3 } + 5 \sqrt { 3 }\)
4. \(12 \sqrt { 6 } + 3 \sqrt { 6 }\)
5. \(4 \sqrt { 5 } - 7 \sqrt { 5 } - 2 \sqrt { 5 }\)
6. \(3 \sqrt { 10 } - 8 \sqrt { 10 } - 2 \sqrt { 10 }\)
7. \(\sqrt { 6 } - 4 \sqrt { 6 } + 2 \sqrt { 6 }\)
8. \(5 \sqrt { 10 } - 15 \sqrt { 10 } - 2 \sqrt { 10 }\)
9. \(13 \sqrt { 7 } - 6 \sqrt { 2 } - 5 \sqrt { 7 } + 5 \sqrt { 2 }\)
10. \(10 \sqrt { 13 } - 12 \sqrt { 15 } + 5 \sqrt { 13 } - 18 \sqrt { 15 }\)
11. \(6 \sqrt { 5 } - ( 4 \sqrt { 3 } - 3 \sqrt { 5 } )\)
12. \(- 12 \sqrt { 2 } - ( 6 \sqrt { 6 } + \sqrt { 2 } )\)
13. \(( 2 \sqrt { 5 } - 3 \sqrt { 10 } ) - ( \sqrt { 10 } + 3 \sqrt { 5 } )\)
14. \(( - 8 \sqrt { 3 } + 6 \sqrt { 15 } ) - ( \sqrt { 3 } - \sqrt { 15 } )\)
15. \(4 \sqrt [ 3 ] { 6 } - 3 \sqrt [ 3 ] { 5 } + 6 \sqrt [ 3 ] { 6 }\)
16. \(\sqrt [ 3 ] { 10 } + 5 \sqrt [ 3 ] { 10 } - 4 \sqrt [ 3 ] { 10 }\)
17. \(( 7 \sqrt [ 3 ] { 9 } - 4 \sqrt [ 3 ] { 3 } ) - ( \sqrt [ 3 ] { 9 } - 3 \sqrt [ 3 ] { 3 } )\)
18. \(( - 8 \sqrt [ 3 ] { 5 } + \sqrt [ 3 ] { 25 } ) - ( 2 \sqrt [ 3 ] { 5 } + 6 \sqrt [ 3 ] { 25 } )\)

Responder

1. \(5 \sqrt { 3 }\)

3. \(14 \sqrt { 3 }\)

5. \(- 5 \sqrt { 5 }\)

7. \(- \sqrt { 6 }\)

9. \(8 \sqrt { 7 } - \sqrt { 2 }\)

11. \(9 \sqrt { 5 } - 4 \sqrt { 3 }\)

13. \(- \sqrt { 5 } - 4 \sqrt { 10 }\)

15. \(10 \sqrt [ 3 ] { 6 } - 3 \sqrt [ 3 ] { 5 }\)

17. \(6 \sqrt [ 3 ] { 9 } - \sqrt [ 3 ] { 3 }\)

Ejercicio\(\PageIndex{4}\)

Simplificar. (Supongamos que todos los radicandos que contienen expresiones variables son positivos.)

1. \(\sqrt { 2 x } - 4 \sqrt { 2 x }\)
2. \(5 \sqrt { 3 y } - 6 \sqrt { 3 y }\)
3. \(9 \sqrt { x } + 7 \sqrt { x }\)
4. \(- 8 \sqrt { y } + 4 \sqrt { y }\)
5. \(7 x \sqrt { y } - 3 x \sqrt { y } + x \sqrt { y }\)
6. \(10 y ^ { 2 } \sqrt { x } - 12 y ^ { 2 } \sqrt { x } - 2 y ^ { 2 } \sqrt { x }\)
7. \(2 \sqrt { a b } - 5 \sqrt { a } + 6 \sqrt { a b } - 10 \sqrt { a }\)
8. \(- 3 x \sqrt { y } + 6 \sqrt { y } - 4 x \sqrt { y } - 7 \sqrt { y }\)
9. \(5 \sqrt { x y } - ( 3 \sqrt { x y } - 7 \sqrt { x y } )\)
10. \(- 8 a \sqrt { b } - ( 2 a \sqrt { b } - 4 \sqrt { a b } )\)
11. \(( 3 \sqrt { 2 x } - \sqrt { 3 x } ) - ( \sqrt { 2 x } - 7 \sqrt { 3 x } )\)
12. \(( \sqrt { y } - 4 \sqrt { 2 y } ) - ( \sqrt { y } - 5 \sqrt { 2 y } )\)
13. \(5 \sqrt [ 3 ] { x } - 12 \sqrt [ 3 ] { x }\)
14. \(- 2 \sqrt [ 3 ] { y } - 3 \sqrt [ 3 ] { y }\)
15. \(a \sqrt [ 5 ] { 3 b } + 4 a \sqrt [ 5 ] { 3 b } - a \sqrt [ 5 ] { 3 b }\)
16. \(- 8 \sqrt [ 4 ] { a b } + 3 \sqrt [ 4 ] { a b } - 2 \sqrt [ 4 ] { a b }\)
17. \(6 \sqrt { 2 a } - 4 \sqrt [ 3 ] { 2 a } + 7 \sqrt { 2 a } - \sqrt [ 3 ] { 2 a }\)
18. \(4 \sqrt [ 5 ] { 3 a } + \sqrt [ 3 ] { 3 a } - 9 \sqrt [ 5 ] { 3 a } + \sqrt [ 3 ] { 3 a }\)
19. \(( \sqrt [ 4 ] { 4 x y } - \sqrt [ 3 ] { x y } ) - ( 2 \sqrt [ 4 ] { 4 x y } - \sqrt [ 3 ] { x y } )\)
20. \(( 5 \sqrt [ 5 ] { 6 y } - 5 \sqrt { y } ) - ( 2 \sqrt [ 6 ] { 6 y } + 3 \sqrt { y } )\)
21. \(2 x ^ { 2 } \sqrt [ 3 ] { 3 x } - \left( x ^ { 2 } \sqrt [ 3 ] { 3 x } - x \sqrt [ 3 ] { 3 x } \right)\)
22. \(5 y ^ { 3 } \sqrt { 6 y } - \left( \sqrt { 6 y } - 4 y ^ { 3 } \sqrt { 6 y } \right)\)

Responder

1. \(- 3 \sqrt { 2 x }\)

3. \(16 \sqrt { x }\)

5. \(5 x \sqrt { y }\)

7. \(8 \sqrt { a b } - 15 \sqrt { a }\)

9. \(9 \sqrt { x y }\)

11. \(2 \sqrt { 2 x } + 6 \sqrt { 3 x }\)

13. \(- 7 \sqrt [ 3 ] { x }\)

15. \(4 a \sqrt [ 5 ] { 3 b }\)

17. \(13 \sqrt { 2 a } - 5 \sqrt [ 3 ] { 2 a }\)

19. \(- \sqrt [ 4 ] { 4 x y }\)

21. \(x ^ { 2 } \sqrt [ 3 ] { 3 x } + x \sqrt [ 3 ] { 3 x }\)

Ejercicio\(\PageIndex{5}\)

Simplificar.

1. \(\sqrt { 75 } - \sqrt { 12 }\)
2. \(\sqrt { 24 } - \sqrt { 54 }\)
3. \(\sqrt { 32 } + \sqrt { 27 } - \sqrt { 8 }\)
4. \(\sqrt { 20 } + \sqrt { 48 } - \sqrt { 45 }\)
5. \(\sqrt { 28 } - \sqrt { 27 } + \sqrt { 63 } - \sqrt { 12 }\)
6. \(\sqrt { 90 } + \sqrt { 24 } - \sqrt { 40 } - \sqrt { 54 }\)
7. \(\sqrt { 45 } - \sqrt { 80 } + \sqrt { 245 } - \sqrt { 5 }\)
8. \(\sqrt { 108 } + \sqrt { 48 } - \sqrt { 75 } - \sqrt { 3 }\)
9. \(4 \sqrt { 2 } - ( \sqrt { 27 } - \sqrt { 72 } )\)
10. \(- 3 \sqrt { 5 } - ( \sqrt { 20 } - \sqrt { 50 } )\)
11. \(\sqrt [ 3 ] { 16 } - \sqrt [ 3 ] { 54 }\)
12. \(\sqrt [ 3 ] { 81 } - \sqrt [ 3 ] { 24 }\)
13. \(\sqrt [ 3 ] { 135 } + \sqrt [ 3 ] { 40 } - \sqrt [ 3 ] { 5 }\)
14. \(\sqrt [ 3 ] { 108 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 4 }\)
15. \(2 \sqrt { 27 } - 2 \sqrt { 12 }\)
16. \(3 \sqrt { 50 } - 4 \sqrt { 32 }\)
17. \(3 \sqrt { 243 } - 2 \sqrt { 18 } - \sqrt { 48 }\)
18. \(6 \sqrt { 216 } - 2 \sqrt { 24 } - 2 \sqrt { 96 }\)
19. \(2 \sqrt { 18 } - 3 \sqrt { 75 } - 2 \sqrt { 98 } + 4 \sqrt { 48 }\)
20. \(2 \sqrt { 45 } - \sqrt { 12 } + 2 \sqrt { 20 } - \sqrt { 108 }\)
21. \(( 2 \sqrt { 363 } - 3 \sqrt { 96 } ) - ( 7 \sqrt { 12 } - 2 \sqrt { 54 } )\)
22. \(( 2 \sqrt { 288 } + 3 \sqrt { 360 } ) - ( 2 \sqrt { 72 } - 7 \sqrt { 40 } )\)
23. \(3 \sqrt [ 3 ] { 54 } + 5 \sqrt [ 3 ] { 250 } - 4 \sqrt [ 3 ] { 16 }\)
24. \(4 \sqrt [ 3 ] { 162 } - 2 \sqrt [ 3 ] { 384 } - 3 \sqrt [ 3 ] { 750 }\)

Responder

1. \(3 \sqrt { 3 }\)

3. \(2 \sqrt { 2 } + 3 \sqrt { 3 }\)

5. \(5 \sqrt { 7 } - 5 \sqrt { 3 }\)

7. \(5 \sqrt { 5 }\)

9. \(10 \sqrt { 2 } - 3 \sqrt { 3 }\)

11. \(- \sqrt [ 3 ] { 2 }\)

13. \(4 \sqrt [ 3 ] { 5 }\)

15. \(2 \sqrt { 3 }\)

17. \(23 \sqrt { 3 } - 6 \sqrt { 2 }\)

19. \(- 8 \sqrt { 2 } + \sqrt { 3 }\)

21. \(8 \sqrt { 3 } - 6 \sqrt { 6 }\)

23. \(26 \sqrt[3] { 2 }\)

Ejercicio\(\PageIndex{6}\)

Simplificar. (Supongamos que todos los radicandos que contienen expresiones variables son positivos.)

1. \(\sqrt { 81 b } + \sqrt { 4 b }\)
2. \(\sqrt { 100 a } + \sqrt { a }\)
3. \(\sqrt { 9 a ^ { 2 } b } - \sqrt { 36 a ^ { 2 } b }\)
4. \(\sqrt { 50 a ^ { 2 } } - \sqrt { 18 a ^ { 2 } }\)
5. \(\sqrt { 49 x } - \sqrt { 9 y } + \sqrt { x } - \sqrt { 4 y }\)
6. \(\sqrt { 9 x } + \sqrt { 64 y } - \sqrt { 25 x } - \sqrt { y }\)
7. \(7 \sqrt { 8 x } - ( 3 \sqrt { 16 y } - 2 \sqrt { 18 x } )\)
8. \(2 \sqrt { 64 y } - ( 3 \sqrt { 32 y } - \sqrt { 81 y } )\)
9. \(2 \sqrt { 9 m ^ { 2 } n } - 5 m \sqrt { 9 n } + \sqrt { m ^ { 2 } n }\)
10. \(4 \sqrt { 18 n ^ { 2 } m } - 2 n \sqrt { 8 m } + n \sqrt { 2 m }\)
11. \(\sqrt { 4 x ^ { 2 } y } - \sqrt { 9 x y ^ { 2 } } - \sqrt { 16 x ^ { 2 } y } + \sqrt { y ^ { 2 } x }\)
12. \(\sqrt { 32 x ^ { 2 } y ^ { 2 } } + \sqrt { 12 x ^ { 2 } y } - \sqrt { 18 x ^ { 2 } y ^ { 2 } } - \sqrt { 27 x ^ { 2 } y }\)
13. \(\left( \sqrt { 9 x ^ { 2 } y } - \sqrt { 16 y } \right) - \left( \sqrt { 49 x ^ { 2 } y } - 4 \sqrt { y } \right)\)
14. \(\left( \sqrt { 72 x ^ { 2 } y ^ { 2 } } - \sqrt { 18 x ^ { 2 } y } \right) - \left( \sqrt { 50 x ^ { 2 } y ^ { 2 } } + x \sqrt { 2 y } \right)\)
15. \(\sqrt { 12 m ^ { 4 } n } - m \sqrt { 75 m ^ { 2 } n } + 2 \sqrt { 27 m ^ { 4 } n }\)
16. \(5 n \sqrt { 27 m n ^ { 2 } } + 2 \sqrt { 12 m n ^ { 4 } } - n \sqrt { 3 m n ^ { 2 } }\)
17. \(2 \sqrt { 27 a ^ { 3 } b } - a \sqrt { 48 a b } - a \sqrt { 144 a ^ { 3 } b }\)
18. \(2 \sqrt { 98 a ^ { 4 } b } - 2 a \sqrt { 162 a ^ { 2 } b } + a \sqrt { 200 b }\)
19. \(\sqrt [ 3 ] { 125 a } - \sqrt [ 3 ] { 27 a }\)
20. \(\sqrt [ 3 ] { 1000 a ^ { 2 } } - \sqrt [ 3 ] { 64 a ^ { 2 } }\)
21. \(2 x \sqrt [ 3 ] { 54 x } - 2 \sqrt [ 3 ] { 16 x ^ { 4 } } + 5 \sqrt [ 3 ] { 2 x ^ { 4 } }\)
22. \(x \sqrt [ 3 ] { 54 x ^ { 3 } } - \sqrt [ 3 ] { 250 x ^ { 6 } } + x ^ { 2 } \sqrt [ 3 ] { 2 }\)
23. \(\sqrt [ 4 ] { 16 y ^ { 2 } } + \sqrt [ 4 ] { 81 y ^ { 2 } }\)
24. \(\sqrt [ 5 ] { 32 y ^ { 4 } } - \sqrt [ 5 ] { y ^ { 4 } }\)
25. \(\sqrt [ 4 ] { 32 a ^ { 3 } } - \sqrt [ 4 ] { 162 a ^ { 3 } } + 5 \sqrt [ 4 ] { 2 a ^ { 3 } }\)
26. \(\sqrt [ 4 ] { 80 a ^ { 4 } b } + \sqrt [ 4 ] { 5 a ^ { 4 } b } - a \sqrt [ 4 ] { 5 b }\)
27. \(\sqrt [ 3 ] { 27 x ^ { 3 } } + \sqrt [ 3 ] { 8 x } - \sqrt [ 3 ] { 125 x ^ { 3 } }\)
28. \(\sqrt [ 3 ] { 24 x } - \sqrt [ 3 ] { 128 x } - \sqrt [ 3 ] { 81 x }\)
29. \(\sqrt [ 3 ] { 27 x ^ { 4 } y } - \sqrt [ 3 ] { 8 x y ^ { 3 } } + x \sqrt [ 3 ] { 64 x y } - y \sqrt [ 3 ] { x }\)
30. \(\sqrt [ 3 ] { 125 x y ^ { 3 } } + \sqrt [ 3 ] { 8 x ^ { 3 } y } - \sqrt [ 3 ] { 216 x y ^ { 3 } } + 10 x ^ { 3 } \sqrt { y }\)
31. \(\left( \sqrt [ 3 ] { 162 x ^ { 4 } y } - \sqrt [ 3 ] { 250 x ^ { 4 } y ^ { 2 } } \right) - \left( \sqrt [ 3 ] { 2 x ^ { 4 } y ^ { 2 } } - \sqrt [ 3 ] { 384 x ^ { 4 } y } \right)\)
32. \(\left( \sqrt [ 5 ] { 32 x ^ { 2 } y ^ { 6 } } - \sqrt [ 5 ] { 243 x ^ { 6 } y ^ { 2 } } \right) - \left( \sqrt [ 5 ] { x ^ { 2 } y ^ { 6 } } - x \sqrt [ 5 ] { x y ^ { 2 } } \right)\)

Responder

1. \(11 \sqrt { b }\)

3. \(- 3 a \sqrt { b }\)

5. \(8 \sqrt { x } - 5 \sqrt { y }\)

7. \(20 \sqrt { 2 x } - 12 \sqrt { y }\)

9. \(- 8 m \sqrt { n }\)

11. \(- 2 x \sqrt { y } - 2 y \sqrt { x }\)

13. \(- 4 x \sqrt { y }\)

15. \(3 m ^ { 2 } \sqrt { 3 n }\)

17. \(2 a \sqrt { 3 a b } - 12 a ^ { 2 } \sqrt { a b }\)

19. \(2 \sqrt [ 3 ] { a }\)

21. \(7 x \sqrt [ 3 ] { 2 x }\)

23. \(5 \sqrt [ 4 ] { y ^ { 2 } }\)

25. \(4 \sqrt [ 4 ] { 2 a ^ { 3 } }\)

27. \(- 2 x + 2 \sqrt [ 3 ] { x }\)

29. \(7 x \sqrt [ 3 ] { x y } - 3 y \sqrt [ 3 ] { x }\)

31. \(7 x \sqrt [ 3 ] { 6 x y } - 6 x \sqrt [ 3 ] { 2 x y ^ { 2 } }\)

Ejercicio\(\PageIndex{7}\)

Calcular los perímetros de los triángulos formados por el siguiente conjunto de vértices.

1. \(\{ ( - 4 , - 5 ) , ( - 4,3 ) , ( 2,3 ) \}\)
2. \(\{ ( - 1,1 ) , ( 3,1 ) , ( 3 , - 2 ) \}\)
3. \(\{ ( - 3,1 ) , ( - 3,5 ) , ( 1,5 ) \}\)
4. \(\{ ( - 3 , - 1 ) , ( - 3,7 ) , ( 1 , - 1 ) \}\)
5. \(\{ ( 0,0 ) , ( 2,4 ) , ( - 2,6 ) \}\)
6. \(\{ ( - 5 , - 2 ) , ( - 3,0 ) , ( 1 , - 6 ) \}\)
7. Un jardín cuadrado que tiene\(10\) pies a cada lado debe ser cercado. Además, el espacio se va a dividir por la mitad utilizando una barda a lo largo de su diagonal. ¿Cuánta esgrima se necesita para hacer esto? (Redondear a la décima de pie más cercana.)
8. Un jardín en forma de cuadrado tiene una superficie de pies\(150\) cuadrados. ¿Cuánto cercado se necesita para cercarlo? (Pista: La longitud de cada lado de un cuadrado es igual a la raíz cuadrada del área. Redondear a la décima de pie más cercana.)

Responder

1. \(24\)unidades

3. \(8 + 4 \sqrt { 2 }\)unidades

5. \(4 \sqrt { 5 } + 2 \sqrt { 10 }\)unidades

7. \(54.1\)pies

Ejercicio\(\PageIndex{8}\)

1. Elija valores para\(x\) y\(y\) y use una calculadora para mostrarlo\(\sqrt { x + y } \neq \sqrt { x } + \sqrt { y }\).
2. Elija valores para\(x\) y\(y\) y use una calculadora para mostrarlo\(\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y\).

Contestar

1. La respuesta puede variar

Notas al pie

¹⁶ Radicales que comparten el mismo índice y radicando.

¹⁷ Término utilizado cuando se refiere a radicales similares.