5.2: Simplificar expresiones radicales

Objetivos de aprendizaje

• Simplifica las expresiones radicales usando la regla de producto y cociente para radicales.
• Usa fórmulas que involucren radicales.

Simplificación de expresiones radicales

Una expresión algebraica que contiene radicales se denomina expresión radical ¹⁴. Utilizamos las reglas de producto y cociente para simplificarlos.

Ejemplo\(\PageIndex{1}\):

Simplificar:\(\sqrt [ 3 ] { 27 x ^ { 3 } }\).

Solución

Usa el hecho de que\(\sqrt [ n ] { a ^ { n } } = a\) cuando\(n\) es extraño.

\(\begin{aligned} \sqrt [ 3 ] { 27 x ^ { 3 } } & = \sqrt [ 3 ] { 3 ^ { 3 } \cdot x ^ { 3 } }\quad\quad \color{Cerulean} { Apply \:the\: product \:rule\: for\: radicals.} \\ & = \sqrt [ 3 ] { 3 ^ { 3 } } \cdot \sqrt [ 3 ] { x ^ { 3 } }\quad \color{Cerulean} { Simplify. } \\ & = 3 \cdot x \\ & = 3 x \end{aligned}\)

Respuesta:

\(3x\)

Ejemplo\(\PageIndex{2}\):

Simplificar:\(\sqrt [ 4 ] { 16 y ^ { 4 } }\).

Solución

Usa el hecho de que\(\sqrt [ n ] { a ^ { n } } = | a |\) cuando\(n\) es parejo.

\(\begin{aligned} \sqrt [ 4 ] { 16 y ^ { 4 } } & = \sqrt [ 4 ] { 2 ^ { 4 } y ^ { 4 } }\quad\quad\:\:\: \color{Cerulean} { Apply\: the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 4 ] { 2 ^ { 4 } } \cdot \sqrt [ 4 ] { y ^ { 4 } }\:\:\:\: \color{Cerulean} { Simplify. } \\ & = 2 \cdot | y | \\ & = 2 | y | \end{aligned}\)

Dado que\(y\) es una variable, puede representar un número negativo. Por lo tanto, debemos asegurarnos de que el resultado sea positivo al incluir el valor absoluto.

Respuesta:

\(2 | y |\)

Nota

Normalmente, en este punto del álgebra observamos que se supone que todas las variables son positivas. Si este es el caso, entonces\(y\) en el ejemplo anterior es positivo y no se necesita el operador de valor absoluto. El ejemplo se puede simplificar de la siguiente manera.

\(\begin{aligned} \sqrt [ 4 ] { 16 y ^ { 4 } } & = \sqrt [ 4 ] { 2 ^ { 4 } y ^ { 4 } } \\ & = \sqrt [ 4 ] { 2 ^ { 4 } } \cdot \sqrt [ 4 ] { y ^ { 4 } } \\ & = 2 y \end{aligned}\)

En esta sección, asumiremos que todas las variables son positivas. Esto nos permite enfocarnos en el cálculo\(n\) de las raíces sin los tecnicismos asociados con el problema principal de raíz\(n\) th. Por esta razón, utilizaremos la siguiente propiedad para el resto de la sección,

\(\sqrt [ n ] { a ^ { n } } = a , \quad \text { if } a \geq 0 \quad \color{Cerulean}{nth \:root}\)

Al simplificar expresiones radicales, busque factores con potencias que coincidan con el índice.

Ejemplo\(\PageIndex{3}\):

Simplificar:\(\sqrt { 12 x ^ { 6 } y ^ { 3 } }\).

Solución

Comience por determinar los factores cuadrados de\(12, x^{ 6}\), y\(y^{ 3}\).

\(\left. \begin{array} { l } { 12 = \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 } \\ { x ^ { 6 } = \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 } }} \\ { y ^ { 3 } = \color{Cerulean}{y ^ { 2} }\color{black}{ \cdot} y } \end{array} \right\} \quad\color{Cerulean}{Square\:factors}\)

Haga estas sustituciones, y luego aplique la regla del producto para los radicales y simplifique.

\(\begin{aligned} \sqrt { 12 x ^ { 6 } y ^ { 3 } } & = \sqrt { \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 \cdot \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 }}\color{black}{ \cdot}\color{Cerulean}{ y ^ { 2} }\color{black}{ \cdot} y } \quad\quad\quad\quad\:\color{Cerulean} { Apply\:the\: product \:rule\: for\: radicals. } \\ & = \sqrt { 2 ^ { 2 } } \cdot \sqrt { \left( x ^ { 3 } \right) ^ { 2 } } \cdot \sqrt { y ^ { 2 } } \cdot \sqrt { 3 y } \quad\color{Cerulean} { Simplify. } \\ & = 2 \cdot x ^ { 3 } \cdot y \cdot \sqrt { 3 y } \\ & = 2 x ^ { 3 } y \sqrt { 3 y } \end{aligned}\)

Respuesta:

\(2 x ^ { 3 } y \sqrt { 3 y }\)

Ejemplo\(\PageIndex{4}\):

Simplificar:\(\sqrt { \frac { 18 a ^ { 5 } } { b ^ { 8 } } }\).

Solución

Comience por determinar los factores cuadrados de\(18\),\(a^{5}\), y\(b^{8}\).

\(\left. \begin{array} { l } { 18 = 2 \cdot \color{Cerulean}{3 ^ { 2} } } \\ { a ^ { 5 } = a ^ { 2 } \cdot a ^ { 2 } \cdot a = \color{Cerulean}{\left( a ^ { 2 } \right) ^ { 2 }}\color{black}{ \cdot} a } \\ { b ^ { 8 } = b ^ { 4 } \cdot b ^ { 4 } \quad\:\:= \color{Cerulean}{\left( b ^ { 4 } \right) ^ { 2 }} } \end{array}\quad \right\}\quad\color{Cerulean}{Square\:factors}\)

Hacer estas sustituciones, aplicar las reglas de producto y cociente para radicales, y luego simplificar.

\(\begin{aligned} \sqrt { \frac { 18 a ^ { 5 } } { b ^ { 8 } } } & = \sqrt { \frac { 2 \cdot \color{Cerulean}{3 ^ { 2} }\color{black}{ \cdot}\color{Cerulean}{ \left( a ^ { 2 } \right) ^ { 2 }}\color{black}{ \cdot} a } { \color{Cerulean}{\left( b ^ { 4 } \right) ^ { 2 } } }}\quad\quad\color{Cerulean}{Apply\:the\:product\:and\:quotient\:rule\:for\:radicals.} \\ & = \frac { \sqrt { 3 ^ { 2 } } \cdot \sqrt { \left( a ^ { 2 } \right) ^ { 2 } } \cdot \sqrt { 2 a } } { \sqrt { \left( b ^ { 4 } \right) ^ { 2 } } }\quad \color{Cerulean}{Simplify.} \\ & = \frac { 3 a ^ { 2 } \sqrt { 2 a } } { b ^ { 4 } } \end{aligned}\)

Respuesta:

\(\frac { 3 a ^ { 2 } \sqrt { 2 a } } { b ^ { 4 } }\)

Ejemplo\(\PageIndex{5}\):

Simplificar:\(\sqrt [ 3 ] { 80 x ^ { 5 } y ^ { 7 } }\).

Solución

Comience por determinar los factores cúbicos de\(80 , x ^ { 5 }\), y\(y^{7}\).

\(\left. \begin{array} { l } { 80 = 2 ^ { 4 } \cdot 5 = \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 \cdot 5 } \\ { x ^ { 5 } = \color{Cerulean}{x ^ { 3 }}\color{black}{ \cdot} x ^ { 2 } } \\ { y ^ { 7 } = y ^ { 6 } \cdot y =\color{Cerulean}{ \left( y ^ { 2 } \right) ^ { 3 } }\color{black}{\cdot} y } \end{array} \quad\right\}\quad\color{Cerulean}{Cubic\:factors}\)

Haga estas sustituciones, y luego aplique la regla del producto para los radicales y simplifique.

\(\begin{aligned} \sqrt [ 3 ] { 80 x ^ { 5 } y ^ { 7 } } & = \sqrt [ 3 ] { \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 \cdot 5 \cdot \color{Cerulean}{x ^ { 3 }}\color{black}{ \cdot} x ^ { 2 } \cdot \color{Cerulean}{\left( y ^ { 2 } \right) ^ { 3 }}\color{black}{ \cdot} y } \\ & = \sqrt [ 3 ] { \color{Cerulean}{2 ^ { 3} } } \color{black}{\cdot} \sqrt [ 3 ] { \color{Cerulean}{x ^ { 3 }} }\color{black}{ \cdot} \sqrt [ 3 ] { \color{Cerulean}{\left( y ^ { 2 } \right) ^ { 3 } } }\color{black}{\cdot} \sqrt [ 3 ] { 2 \cdot 5 \cdot x ^ { 2 } \cdot y } \\ & = 2 \cdot x y ^ { 2 } \cdot \sqrt [ 3 ] { 10 x ^ { 2 } y } \\ & = 2 x y ^ { 2 } \sqrt [ 3 ] { 10 x ^ { 2 } y } \end{aligned}\)

Respuesta:

\(2 x y ^ { 2 } \sqrt [ 3 ] { 10 x ^ { 2 } y }\)

Ejemplo\(\PageIndex{6}\):

Simplificar:\(\sqrt [ 3 ] { \frac { 9 x ^ { 6 } } { y ^ { 3 } z ^ { 9 } } }\).

Solución

El coeficiente\(9 = 3^{2}\), y por lo tanto no tiene ningún factor cubo perfecto. Se dejará como el único radical restante porque todos los demás factores son cubos, como se ilustra a continuación:

\(\left. \begin{array} { l } { x ^ { 6 } = \left( x ^ { 2 } \right) ^ { 3 } } \\ { y ^ { 3 } = ( y ) ^ { 3 } } \\ { z ^ { 9 } = \left( z ^ { 3 } \right) ^ { 3 } } \end{array} \quad\right\}\quad\color{Cerulean}{Cubic\:factors}\)

Reemplazar las variables con estos equivalentes, aplicar las reglas de producto y cociente para radicales, y luego simplificar.

\(\begin{aligned} \sqrt [ 3 ] { \frac { 9 x ^ { 6 } } { y ^ { 3 } z ^ { 9 } } } & = \sqrt [ 3 ] { \frac { 9 \cdot \left( x ^ { 2 } \right) ^ { 3 } } { y ^ { 3 } \cdot \left( z ^ { 3 } \right) ^ { 3 } } } \\ & = \frac { \sqrt [ 3 ] { 9 } \cdot \sqrt [ 3 ] { \left( x ^ { 2 } \right) ^ { 3 } } } { \sqrt [ 3 ] { y ^ { 3 } } \cdot \sqrt [ 3 ] { \left( z ^ { 3 } \right) ^ { 3 } } } \\ & = \frac{\sqrt[3]{9} \:\cdot\:x^{2} }{y\:\cdot\:z^{3}}\\&= \frac{x^{2}\:\sqrt[3]{9}}{yz^{3}}\end{aligned}\)

Respuesta:

\(\frac { x ^ { 2 } \sqrt [ 3 ] { 9 } } { y z ^ { 3 } }\)

Ejemplo\(\PageIndex{7}\):

Simplificar:\(\sqrt [ 4 ] { 81 a ^ { 4 } b ^ { 5 } }\).

Solución

Determinar todos los factores que se pueden escribir como poderes perfectos de\(4\). Aquí, es importante verlo\(b^{5} = b^{4} ⋅ b\). De ahí que el factor\(b\) quede dentro del radical.

\(\begin{aligned} \sqrt [ 4 ] { 81 a ^ { 4 } b ^ { 5 } } & = \sqrt [ 4 ] { 3 ^ { 4 } \cdot a ^ { 4 } \cdot b ^ { 4 } \cdot b } \\ & = \sqrt [ 4 ] { 3 ^ { 4 } } \cdot \sqrt [ 4 ] { a ^ { 4 } } \cdot \sqrt [ 4 ] { b ^ { 4 } } \cdot \sqrt [ 4 ] { b } \\ & = 3 \cdot a \cdot b \cdot \sqrt [ 4 ] { b } \\ & = 3 a b \sqrt [ 4 ] { b } \end{aligned}\)

Respuesta:

\(3 a b \sqrt [ 4 ] { b }\)

Ejemplo\(\PageIndex{8}\):

Simplificar:\(\sqrt [ 5 ] { - 32 x ^ { 3 } y ^ { 6 } z ^ { 5 } }\).

Solución

Observe que el factor variable\(x\) no puede escribirse como un poder de\(5\) y así quedará dentro del radical. Además,\(y^{6} = y^{5} ⋅ y\); el factor\(y\) quedará dentro del radical también.

\(\begin{aligned} \sqrt [ 3 ] { - 32 x ^ { 3 } y ^ { 6 } z ^ { 5 } } & = \sqrt [ 5 ] { \color{Cerulean}{( - 2 ) ^ { 5 } }\color{black}{\cdot} x ^ { 3 } \cdot\color{Cerulean}{ y ^ { 5} }\color{black}{ \cdot} y \cdot \color{Cerulean}{z ^ { 5} } } \\ & = \sqrt [ 5 ] {\color{Cerulean}{ ( - 2 ) ^ { 5 } }} \color{black}{\cdot} \sqrt [ 5 ] { \color{Cerulean}{y ^ { 5 }} }\color{black}{ \cdot} \sqrt [ 5 ] { \color{Cerulean}{z ^ { 5} } }\color{black}{ \cdot} \sqrt [ 5 ] { x ^ { 3 } \cdot y } \\ & = - 2 \cdot y \cdot z \cdot \sqrt [ 5 ] { x ^ { 3 } \cdot y } \\ & = - 2 y z \sqrt [ 5 ] { x ^ { 3 } y } \end{aligned}\)

Respuesta:

\(- 2 y z \sqrt [ 5 ] { x ^ { 3 } y }\)

Consejo: Para simplificar la búsqueda de una raíz\(n\) th, divida las potencias por el índice.

\(\begin{aligned} \sqrt { a ^ { 6 } } = a ^ { 3 } , & \text { which is } a ^ { 6 \div 2 } = a ^ { 3 } \\ \sqrt [ 3 ] { b ^ { 6 } } = b ^ { 2 } , & \text { which is } b ^ { 6 \div 3 } = b ^ { 2 } \\ \sqrt[6]{c^{6}} = c\:\:, &\: \text{which is} \:{c^{6\div 6} = c^{1}} \end{aligned}\)

Si el índice no divide en la potencia de manera uniforme, entonces podemos usar el cociente y el resto para simplificar. Por ejemplo,

\(\begin{aligned} \sqrt { a ^ { 5 } }& = a ^ { 2 } \cdot \sqrt { a } , \text { which is } a ^ { 5 \div 2 } = a ^ { 2 r 1 } \\ \sqrt [ 3 ] { b ^ { 5 } }& = b \cdot \sqrt [ 3 ] { b ^ { 2 } } , \text { which is } b ^ { 5 \div 3 } = b ^ { 1 r 2 } \\ \sqrt[5]{c^{14}} &= c^{2} \cdot\sqrt[5]{c^{4}}, \text{which is} \:c^{14\div 5} = c^{2r4} \end{aligned}\)

El cociente es el exponente del factor fuera del radical, y el resto es el exponente del factor que queda dentro del radical.

Ejercicio\(\PageIndex{1}\)

Simplificar:\(\sqrt [ 3 ] { 162 a ^ { 7 } b ^ { 5 } c ^ { 4 } }\).

Responder

\(3 a ^ { 2 } b c \sqrt [ 3 ] { 6 a b ^ { 2 } c }\)

www.youtube.com/V/KT9QA1NFMLK

Fórmulas que involucran radicales

Las fórmulas suelen consistir en expresiones radicales. Por ejemplo, el periodo de un péndulo, o el tiempo que tarda un péndulo en oscilar de un lado a otro y hacia atrás, depende de su longitud según la siguiente fórmula.

\(T = 2 \pi \sqrt { \frac { L } { 32 } }\)

Aquí\(T\) representa el periodo en segundos y\(L\) representa la longitud en pies del péndulo.

Ejemplo\(\PageIndex{9}\):

Si la longitud de un péndulo mide\(1 \frac{1}{2}\) pies, entonces calcula el período redondeado a la décima de segundo más cercana.

Solución

Sustituir\(1 \frac{1}{2} = \frac{3}{2}\)\(L\) y luego simplificar.

\(\begin{aligned} T & = 2 \pi \sqrt { \frac { L } { 32 } } \\ & = 2 \pi \sqrt { \frac { \frac{3}{2} } { 32 } } \\ & = 2 \pi \sqrt { \frac { 3 } { 2 } \cdot \frac { 1 } { 32 } } \quad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals.} \\ & = 2 \pi \frac { \sqrt { 3 } } { \sqrt { 64 } }\quad\quad\:\:\:\color{Cerulean}{Simplify.} \\ & = \frac { \pi \sqrt { 3 } } { 4 } \approx 1.36 \end{aligned}\)

Respuesta:

El periodo es de aproximadamente\(1.36\) segundos.

Frecuentemente es necesario calcular la distancia entre dos puntos en un plano. Para ello, formar un triángulo rectángulo usando los dos puntos como vértices del triángulo y luego aplicar el teorema de Pitágoras. Recordemos que el teorema de Pitágoras establece que si se le da algún triángulo rectángulo con patas de medición\(a\) y\(b\) unidades, entonces el cuadrado de la medida de la hipotenusa\(c\) es igual a la suma de los cuadrados de las piernas:\(a^{2} + b^{2} = c^{2}\). Es decir, la hipotenusa de cualquier triángulo rectángulo es igual a la raíz cuadrada de la suma de los cuadrados de sus patas.

Figura\(\PageIndex{1}\)

Ejemplo\(\PageIndex{10}\):

Encuentra la distancia entre\((-5,3)\) y\((1,1)\).

Solución

Formar un triángulo rectángulo dibujando líneas horizontales y verticales a través de los dos puntos. Esto crea un triángulo rectángulo como se muestra a continuación:

Figura\(\PageIndex{2}\)

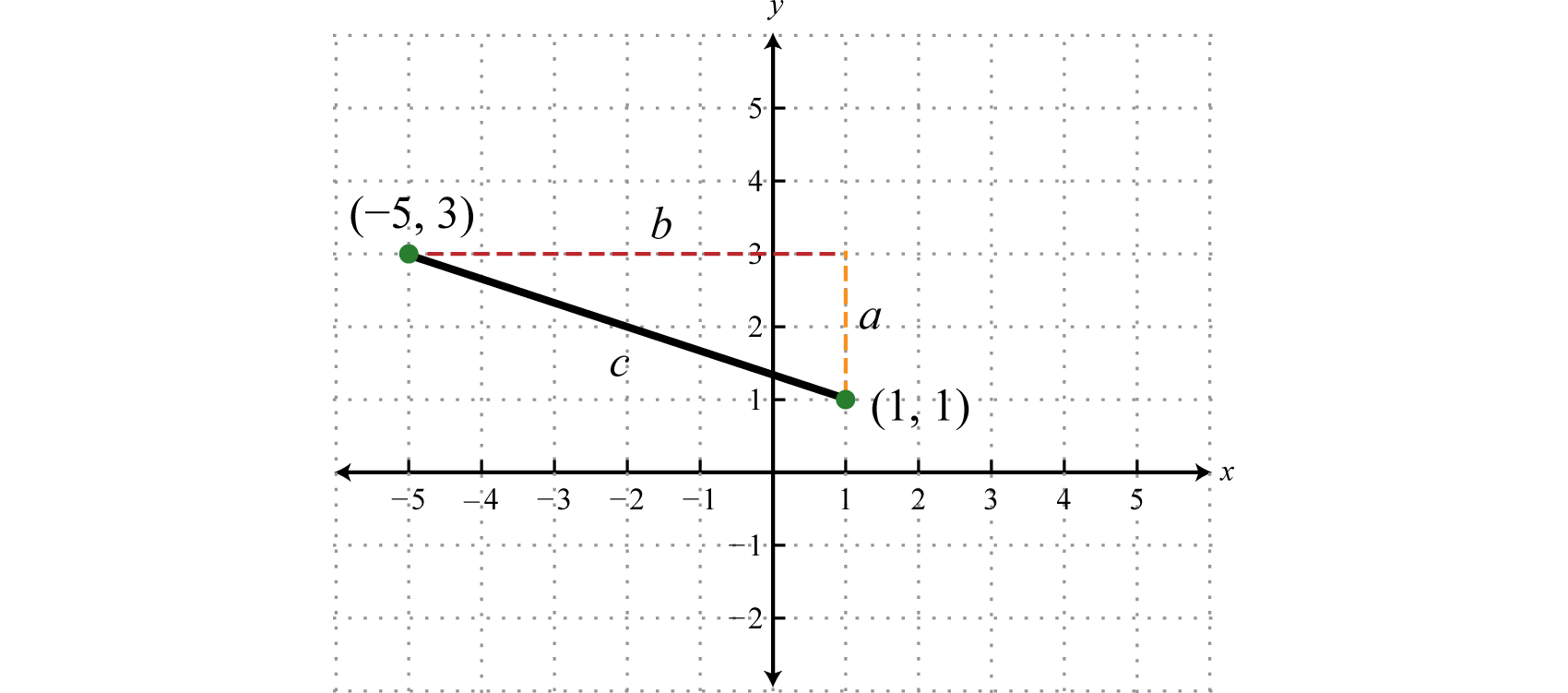
La longitud de pierna\(b\) se calcula encontrando la distancia entre los\(x\) -valores de los puntos dados, y la longitud de pierna\(a\) se calcula encontrando la distancia entre los\(y\) valores dados.

\(\begin{array} { l } { a = 3 - 1 = 2 \text { units } } \\ { b = 1 - ( - 5 ) = 1 + 5 = 6 \text { units } } \end{array}\)

A continuación, utilice el teorema de Pitágoras para encontrar la longitud de la hipotenusa.

\(\begin{aligned} c & = \sqrt { 2 ^ { 2 } + 6 ^ { 2 } } \\ & = \sqrt { 4 + 36 } \\ & = \sqrt { 40 } \\ & = \sqrt { 4 \cdot 10 } \\ & = 2 \sqrt { 10 } \text { units } \end{aligned}\)

Respuesta:

La distancia entre los dos puntos es\(2 \sqrt{10}\) unidades.

Generalizar este proceso para producir una fórmula que pueda ser utilizada para calcular algebraicamente la distancia entre dos puntos dados cualquiera.

Figura\(\PageIndex{3}\)

Dados dos puntos,\(\left( x _ { 1 } , y _ { 1 } \right)\) y\(\left( x _ { 2 } , y _ { 2 } \right)\) la distancia,\(d|), between them is given by the distance formula¹⁵, \(d = \sqrt { \left( x _ { 2 } - x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } - y _ { 1 } \right) ^ { 2 } }\).

Ejemplo\(\PageIndex{11}\):

Calcular la distancia entre\((-4,7)\) y\((2,1)\).

Solución

Utilice la fórmula de distancia con los siguientes puntos.

\(\begin{array} { l } { \left( x _ { 1 } , y _ { 1 } \right) \left( x _ { 2 } , y _ { 2 } \right) } \\ { (\color{Cerulean}{ - 4}\color{black}{,}\color{OliveGreen}{7}\color{black}{ )} \quad ( \color{Cerulean}{2}\color{black}{,}\color{OliveGreen}{1}\color{black}{ )} } \end{array}\)

Es una buena práctica incluir la fórmula en su forma general antes de sustituir valores por las variables; esto mejora la legibilidad y reduce la probabilidad de cometer errores.

\(\begin{aligned} d & = \sqrt { \left( x _ { 2 } - x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } - y _ { 1 } \right) ^ { 2 } } \\ & = \sqrt { ( \color{Cerulean}{2}\color{black}{ -} ( \color{Cerulean}{- 4}\color{black}{ )} ) ^ { 2 } + ( \color{OliveGreen}{1}\color{black}{ -}\color{OliveGreen}{ 7}\color{black}{ )} ^ { 2 } } \\ & = \sqrt { ( 2 + 4 ) ^ { 2 } + ( 1 - 7 ) ^ { 2 } } \\ & = \sqrt { ( 6 ) ^ { 2 } + ( - 6 ) ^ { 2 } } \\ & = \sqrt { 72 }\\ & = \sqrt{36\cdot2} \\ & = 6 \sqrt { 2 } \end{aligned}\)

Respuesta:

La distancia entre los dos puntos es\(6\sqrt{2}\) unidades.

Ejemplo\(\PageIndex{12}\):

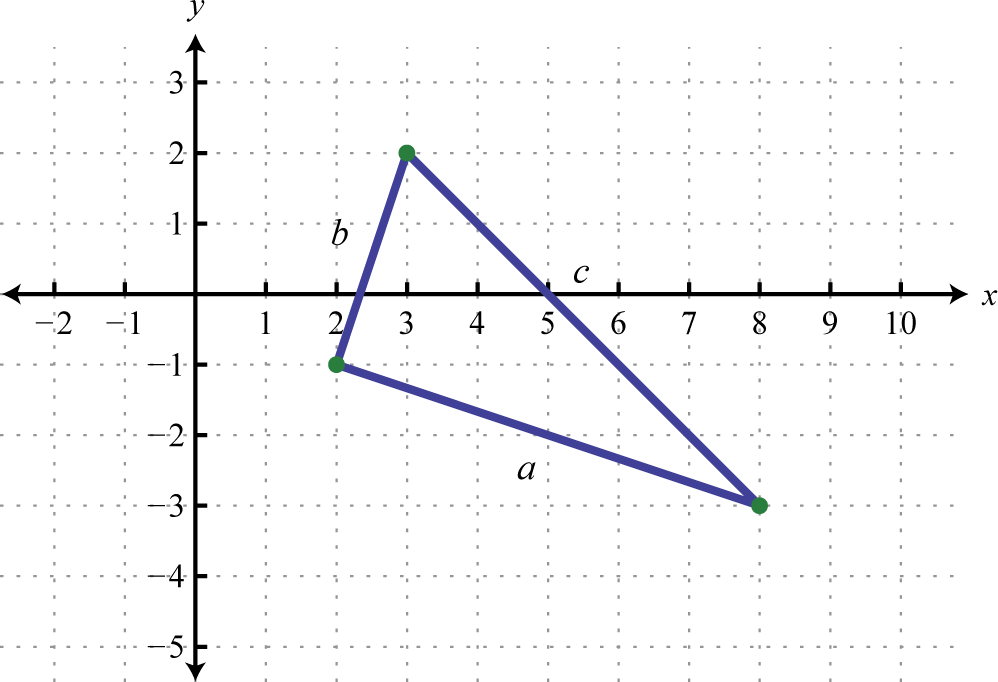
¿Los tres puntos\(( 2 , - 1 ) , ( 3,2 )\), y\((8,-3)\) forman un triángulo rectángulo?

Solución

El teorema de Pitágoras afirma que tener longitudes laterales que satisfagan la propiedad\(a^{2} + b^{2}= c^{2}\) es una condición necesaria y suficiente de los triángulos rectos. Es decir, si puedes demostrar que la suma de los cuadrados de las longitudes de las patas del triángulo es igual al cuadrado de la longitud de la hipotenusa, entonces el triángulo debe ser un triángulo rectángulo. Primero, calcule la longitud de cada lado usando la fórmula de distancia.

Mesa\(\PageIndex{1}\)

Geometría	Cálculo
Figura\(\PageIndex{4}\)	Puntos:\((2,-1)\) y\((8,-3)\) \(\begin{array} { l } { a = \sqrt { ( 8 - 2 ) ^ { 2 } + [ - 3 - ( - 1 ) ] ^ { 2 } } } \\ { = \sqrt { ( 6 ) ^ { 2 } + ( - 3 + 1 ) ^ { 2 } } } \\ { = \sqrt { 36 + ( - 2 ) ^ { 2 } } } \\ { = \sqrt { 36 + 4 } } \\ { = \sqrt{40} } \\ { = 2 \sqrt { 10 } } \end{array}\)
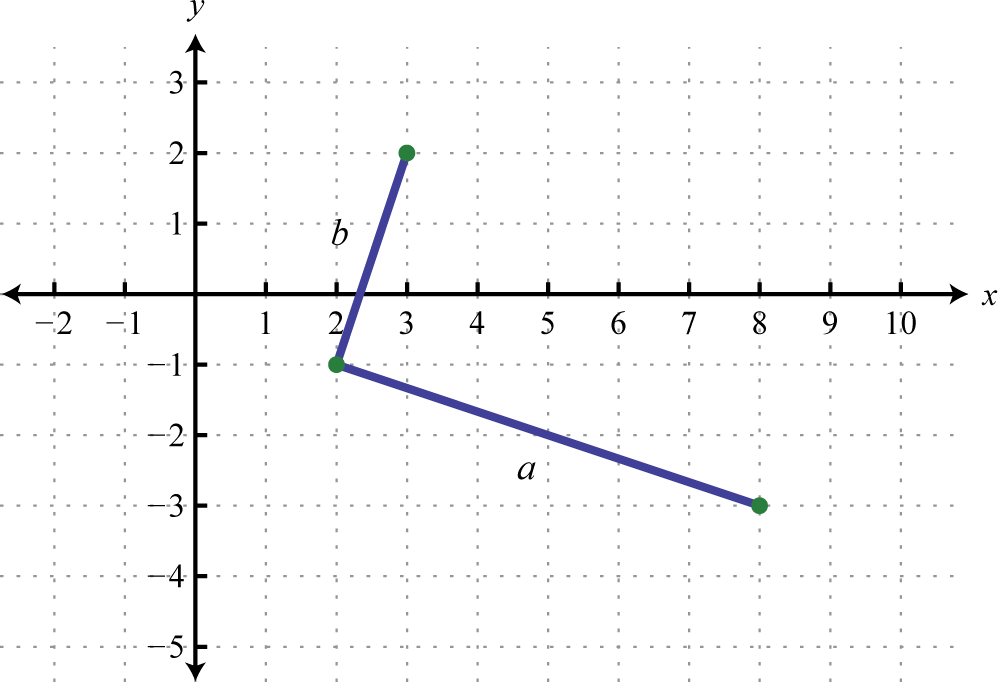Figura\(\PageIndex{5}\)	Puntos:\((2,-1)\) y\((3,2)\) \(\begin{array} { l } { b = \sqrt { ( 3 - 2 ) ^ { 2 } + [ 2 - ( - 1 ) ] ^ { 2 } } } \\ { = \sqrt { ( 1 ) ^ { 2 } + ( 2 + 1 ) ^ { 2 } } } \\ = \sqrt{1+ (3)^{2}}\\{ = \sqrt { 1 + 9 } } \\ { = \sqrt { 10 } } \end{array}\)
Figura\(\PageIndex{6}\)	Puntos:\((3,2)\) y\((8,-3)\) \(\begin{array} { l } { c = \sqrt { ( 8 - 3 ) ^ { 2 } + ( - 3 - 2 ) ^ { 2 } } } \\ { = \sqrt { ( 5 ) ^ { 2 } + ( - 5 ) ^ { 2 } } } \\ { = \sqrt { 25 + 25 } } \\ { = \sqrt { 50 } } \\ { = 5 \sqrt { 2 } } \end{array}\)

Ahora comprobamos para ver si\(a ^ { 2 } + b ^ { 2 } = c ^ { 2 }\).

\(\begin{aligned} a ^ { 2 } + b ^ { 2 } & = c ^ { 2 } \\ ( 2 \sqrt { 10 } ) ^ { 2 } + ( \sqrt { 10 } ) ^ { 2 } &= ( 5 \sqrt { 2 } ) ^ { 2 } \\ 4 ( \sqrt { 10 } ) ^ { 2 } + ( \sqrt { 10 } ) ^ { 2 } & = 25 ( \sqrt { 2 } ) ^ { 2 } \\ 4 \cdot 10 + 10 &= 25 \cdot 2 \\ 50 &= 50 \:\:\color{Cerulean}{✓}\end{aligned}\)

Respuesta:

Sí, los tres puntos forman un triángulo rectángulo.

Ejercicio\(\PageIndex{2}\)

La velocidad de un vehículo antes de que se aplicaran los frenos se puede estimar por la longitud de las marcas de derrape dejadas en la carretera. En concreto húmedo, la velocidad\(v\) en millas por hora se puede estimar por la fórmula\(v = 2 \sqrt { 3 d }\), donde\(d\) representa la longitud de las marcas de derrape en pies. Estime la velocidad de un vehículo antes de aplicar los frenos si las marcas de derrape dejadas miden\(27\) los pies. Redondear a la milla por hora más cercana.

Responder

\(18\)millas por hora

www.youtube.com/v/8iscyu3ywqw

Claves para llevar

• Para simplificar una expresión radical, buscar factores del radicando con potencias que coincidan con el índice. Si se encuentran, pueden simplificarse aplicando las reglas de producto y cociente para radicales, así como la propiedad\(\sqrt [ n ] { a ^ { n } } = a\), donde\(a\) es no negativa.
• Una expresión radical se simplifica si su radicando no contiene ningún factor que pueda escribirse como poderes perfectos del índice.
• Normalmente asumimos que todas las expresiones variables dentro del radical no son negativas. Esto nos permite enfocarnos en simplificar los radicales sin los problemas técnicos asociados con la\(n\) raíz principal. Si no se hace esta suposición, aseguraremos un resultado positivo mediante el uso de valores absolutos a la hora de simplificar los radicales con índices pares.

Ejercicio\(\PageIndex{3}\)

Supongamos que la variable podría representar cualquier número real y luego simplificar.

1. \(\sqrt { 9 x ^ { 2 } }\)
2. \(\sqrt { 16 y ^ { 2 } }\)
3. \(\sqrt [ 3 ] { 8 y ^ { 3 } }\)
4. \(\sqrt [ 3 ] { 125 a ^ { 3 } }\)
5. \(\sqrt [ 4 ] { 64 x ^ { 4 } }\)
6. \(\sqrt [ 4 ] { 81 y ^ { 4 } }\)
7. \(\sqrt { 36 a ^ { 4 } }\)
8. \(\sqrt { 100 a ^ { 8 } }\)
9. \(\sqrt { 4 a ^ { 6 } }\)
10. \(\sqrt { a ^ { 10 } }\)
11. \(\sqrt { 18 a ^ { 4 } b ^ { 5 } }\)
12. \(\sqrt { 48 a ^ { 5 } b ^ { 3 } }\)
13. \(\sqrt [ 6 ] { 128 x ^ { 6 } y ^ { 8 } }\)
14. \(\sqrt [ 6 ] { a ^ { 6 } b ^ { 7 } c ^ { 8 } }\)
15. \(\sqrt { ( 5 x - 4 ) ^ { 2 } }\)
16. \(\sqrt { ( 3 x - 5 ) ^ { 4 } }\)
17. \(\sqrt { x ^ { 2 } - 6 x + 9 }\)
18. \(\sqrt { x ^ { 2 } - 10 x + 25 }\)
19. \(\sqrt { 4 x ^ { 2 } + 12 x + 9 }\)
20. \(\sqrt { 9 x ^ { 2 } + 6 x + 1 }\)

Responder

1. \(3 | x |\)

3. \(2y\)

5. \(2 | x |\)

7. \(6 a ^ { 2 }\)

9. \(2 \left| a ^ { 3 } \right|\)

11. \(3 a ^ { 2 } b ^ { 2 } \sqrt { 2 b }\)

13. \(2 | x y | \sqrt [ 6 ] { 2 y ^ { 2 } }\)

15. \(| 5 x - 4 |\)

17. \(| x - 3 |\)

19. \(| 2x + 3 |\)

Ejercicio\(\PageIndex{4}\)

Simplificar. (Supongamos que todas las expresiones variables representan números positivos.)

1. \(\sqrt { 49 a ^ { 2 } }\)
2. \(\sqrt { 64 b ^ { 2 } }\)
3. \(\sqrt { x ^ { 2 } y ^ { 2 } }\)
4. \(\sqrt { 25 x ^ { 2 } y ^ { 2 } z ^ { 2 } }\)
5. \(\sqrt { 180 x ^ { 3 } }\)
6. \(\sqrt { 150 y ^ { 3 } }\)
7. \(\sqrt { 49 a ^ { 3 } b ^ { 2 } }\)
8. \(\sqrt { 4 a ^ { 4 } b ^ { 3 } c }\)
9. \(\sqrt { 45 x ^ { 5 } y ^ { 3 } }\)
10. \(\sqrt { 50 x ^ { 6 } y ^ { 4 } }\)
11. \(\sqrt { 64 r ^ { 2 } s ^ { 6 } t ^ { 5 } }\)
12. \(\sqrt { 144 r ^ { 8 } s ^ { 6 } t ^ { 2 } }\)
13. \(\sqrt { ( x + 1 ) ^ { 2 } }\)
14. \(\sqrt { ( 2 x + 3 ) ^ { 2 } }\)
15. \(\sqrt { 4 ( 3 x - 1 ) ^ { 2 } }\)
16. \(\sqrt { 9 ( 2 x + 3 ) ^ { 2 } }\)
17. \(\sqrt { \frac { 9 x ^ { 3 } } { 25 y ^ { 2 } } }\)
18. \(\sqrt { \frac { 4 x ^ { 5 } } { 9 y ^ { 4 } } }\)
19. \(\sqrt { \frac { m ^ { 7 } } { 36 n ^ { 4 } } }\)
20. \(\sqrt { \frac { 147 m ^ { 9 } } { n ^ { 6 } } }\)
21. \(\sqrt { \frac { 2 r ^ { 2 } s ^ { 5 } } { 25 t ^ { 4 } } }\)
22. \(\sqrt { \frac { 36 r ^ { 5 } } { s ^ { 2 } t ^ { 6 } } }\)
23. \(\sqrt [ 3 ] { 27 a ^ { 3 } }\)
24. \(\sqrt [ 3 ] { 125 b ^ { 3 } }\)
25. \(\sqrt [ 3 ] { 250 x ^ { 4 } y ^ { 3 } }\)
26. \(\sqrt [ 3 ] { 162 a ^ { 3 } b ^ { 5 } }\)
27. \(\sqrt [ 3 ] { 64 x ^ { 3 } y ^ { 6 } z ^ { 9 } }\)
28. \(\sqrt [ 3 ] { 216 x ^ { 12 } y ^ { 3 } }\)
29. \(\sqrt [ 3 ] { 8 x ^ { 3 } y ^ { 4 } }\)
30. \(\sqrt [ 3 ] { 27 x ^ { 5 } y ^ { 3 } }\)
31. \(\sqrt [ 3 ] { a ^ { 4 } b ^ { 5 } c ^ { 6 } }\)
32. \(\sqrt [ 3 ] { a ^ { 7 } b ^ { 5 } c ^ { 3 } }\)
33. \(\sqrt [ 3 ] { \frac { 8 x ^ { 4 } } { 27 y ^ { 3 } } }\)
34. \(\sqrt [ 3 ] { \frac { x ^ { 5 } } { 125 y ^ { 6 } } }\)
35. \(\sqrt [ 3 ] { 360 r ^ { 5 } s ^ { 12 } t ^ { 13 } }\)
36. \(\sqrt [ 3 ] { 540 r ^ { 3 } s ^ { 2 } t ^ { 9 } }\)
37. \(\sqrt [ 4 ] { 81 x ^ { 4 } }\)
38. \(\sqrt [ 4 ] { x ^ { 4 } y ^ { 4 } }\)
39. \(\sqrt [ 4 ] { 16 x ^ { 4 } y ^ { 8 } }\)
40. \(\sqrt [ 4 ] { 81 x ^ { 12 } y ^ { 4 } }\)
41. \(\sqrt [ 4 ] { a ^ { 4 } b ^ { 5 } c ^ { 6 } }\)
42. \(\sqrt [ 4 ] { 5 ^ { 4 } a ^ { 6 } c ^ { 8 } }\)
43. \(\sqrt [ 4 ] { 128 x ^ { 6 } }\)
44. \(\sqrt [ 4 ] { 243 y ^ { 7 } }\)
45. \(\sqrt [ 5 ] { \frac { 32 m ^ { 10 } } { n ^ { 5 } } }\)
46. \(\sqrt [ 5 ] { \frac { 3 ^ { 7 } m ^ { 9 } } { n ^ { 10 } } }\)
47. \(- 3 \sqrt { 4 x ^ { 2 } }\)
48. \(7 \sqrt { 9 y ^ { 2 } }\)
49. \(- 5 x \sqrt { 4 x ^ { 2 } y }\)
50. \(- 3 y \sqrt { 16 x ^ { 3 } y ^ { 2 } }\)
51. \(12 a b \sqrt { a ^ { 5 } b ^ { 3 } }\)
52. \(6 a ^ { 2 } b \sqrt { 9 a ^ { 7 } b ^ { 2 } }\)
53. \(2 x \sqrt [ 3 ] { 8 x ^ { 6 } }\)
54. \(- 5 x ^ { 2 } \sqrt [ 3 ] { 27 x ^ { 3 } }\)
55. \(2 a b \sqrt [ 3 ] { - 8 a ^ { 4 } b ^ { 5 } }\)
56. \(5 a ^ { 2 } b \sqrt [ 3 ] { - 27 a ^ { 3 } b ^ { 3 } }\)

Responder

1. \(7a\)

3. \(xy\)

5. \(6 x \sqrt { 5 x }\)

7. \(7 a b \sqrt { a }\)

9. \(3 x ^ { 2 } y \sqrt { 5 x y }\)

11. \(8 r s ^ { 3 } t ^ { 2 } \sqrt { t }\)

13. \(x + 1\)

15. \(2 ( 3 x - 1 )\)

17. \(\frac { 3 x \sqrt { x } } { 5 y }\)

19. \(\frac { m ^ { 3 } \sqrt { m } } { 6 n ^ { 2 } }\)

21. \(\frac { r s ^ { 2 } \sqrt { 2 s } } { 5 t ^ { 2 } }\)

23. \(3 a\)

25. \(5 x y \sqrt [ 3 ] { 2 x }\)

27. \(4 x y ^ { 2 } z ^ { 3 }\)

29. \(2 x y \sqrt [ 3 ] { y }\)

31. \(a b c ^ { 2 } \sqrt [ 3 ] { a b ^ { 2 } }\)

33. \(\frac { 2 x \sqrt [ 3 ] { x } } { 3 y }\)

35. \(2 r s ^ { 4 } t ^ { 4 } \sqrt [ 3 ] { 45 r ^ { 2 } t }\)

37. \(3 x\)

39. \(2xy^{2}\)

41. \(a b c \sqrt [ 4 ] { b c ^ { 2 } }\)

43. \(2 x \sqrt [ 4 ] { 8 x ^ { 2 } }\)

45. \(\frac { 2 m ^ { 2 } } { n }\)

47. \(-6x\)

49. \(- 10 x ^ { 2 } \sqrt { y }\)

51. \(12 a ^ { 3 } b ^ { 2 } \sqrt { a b }\)

53. \(4 x ^ { 3 }\)

55. \(- 4 a ^ { 2 } b ^ { 2 } \sqrt [ 3 ] { a b ^ { 2 } }\)

Ejercicio\(\PageIndex{5}\)

Reescribe lo siguiente como una expresión radical con coeficiente\(1\).

1. \(3 x \sqrt { 6 x }\)
2. \(5 y \sqrt { 5 y }\)
3. \(a b \sqrt { 10 a }\)
4. \(2 a b ^ { 2 } \sqrt { a }\)
5. \(m ^ { 2 } n \sqrt { m n }\)
6. \(2 m ^ { 2 } n ^ { 3 } \sqrt { 3 n }\)
7. \(2 x \sqrt [ 3 ] { 3 x }\)
8. \(3 y \sqrt [ 3 ] { y ^ { 2 } }\)
9. \(2 y ^ { 2 } \sqrt [ 4 ] { 4 y }\)
10. \(x ^ { 2 } y \sqrt [ 5 ] { 9 x y ^ { 2 } }\)

Responder

1. \(\sqrt { 54 x ^ { 3 } }\)

3. \(\sqrt { 10 a ^ { 3 } b ^ { 2 } }\)

5. \(\sqrt { m ^ { 5 } n ^ { 3 } }\)

7. \(\sqrt [ 3 ] { 24 x ^ { 4 } }\)

9. \(\sqrt [ 4 ] { 64 y ^ { 9 } }\)

Ejercicio\(\PageIndex{6}\)

El periodo\(T\) en segundos de un péndulo viene dado por la fórmula

\(T = 2 \pi \sqrt { \frac { L } { 32 } }\)

donde\(L\) representa la longitud en pies del péndulo. Calcular el periodo, dada cada una de las siguientes longitudes. Dar el valor exacto y el valor aproximado redondeado a la décima de segundo más cercana.

1. \(8\)pies
2. \(32\)pies
3. \(\frac{1}{2}\)pie
4. \(\frac{1}{8}\)pie

Responder

1. \(π\)segundos;\(3.1\) segundos

3. \(\frac { \pi } { 4 }\)segundos;\(0.8\) segundos

Ejercicio\(\PageIndex{7}\)

El tiempo\(t\) en segundos que un objeto está en caída libre viene dado por la fórmula

\(t = \frac { \sqrt { s } } { 4 }\)

donde\(s\) representa la distancia en pies que ha caído el objeto. Calcula el tiempo que tarda un objeto en caer, dadas cada una de las siguientes distancias. Dar el valor exacto y el valor aproximado redondeado a la décima de segundo más cercana.

1. \(48\)pies
2. \(80\)pies
3. \(192\)pies
4. \(288\)pies
5. La velocidad de un vehículo antes de que se aplicaran los frenos se puede estimar por la longitud de las marcas de derrape dejadas en la carretera. En pavimento seco, la velocidad\(v\) en millas por hora se puede estimar por la fórmula\(v = 2 \sqrt { 6 d }\), donde\(d\) representa la longitud de las marcas de derrape en pies. Estime la velocidad de un vehículo antes de aplicar los frenos sobre pavimento seco si las marcas de derrape dejadas miden\(27\) pies. Redondear a la milla por hora más cercana.
6. El radio\(r\) de una esfera se puede calcular usando la fórmula\(r = \frac { \sqrt [ 3 ] { 6 \pi ^ { 2 } V } } { 2 \pi }\), donde\(V\) representa el volumen de la esfera. ¿Cuál es el radio de una esfera si el volumen es de centímetros\(36π\) cúbicos?

Responder

1. \(\sqrt{3}\)segundos;\(1.7\) segundos

3. \(2\sqrt{3}\)segundos;\(3.5\) segundos

5. \(25\)millas por hora

Ejercicio\(\PageIndex{8}\)

Dada la función encontrar el\(y\) -intercept

1. \(f ( x ) = \sqrt { x + 12 }\)
2. \(f ( x ) = \sqrt { x + 8 } - 3\)
3. \(f ( x ) = \sqrt [ 3 ] { x - 8 }\)
4. \(f ( x ) = \sqrt [ 3 ] { x + 27 }\)
5. \(f ( x ) = \sqrt [ 3 ] { x + 16 }\)
6. \(f ( x ) = \sqrt [ 3 ] { x + 3 } - 1\)

Responder

1. \(( 0,2 \sqrt { 3 } )\)

3. \((0,-2)\)

5. \(( 0,2 \sqrt [ 3 ] { 2 } )\)

Ejercicio\(\PageIndex{9}\)

Usa la fórmula de distancia para calcular la distancia entre los dos puntos dados.

1. \((5,-7)\)y\((3,-8)\)
2. \((-9,7)\)y\((-8,4)\)
3. \((-3,-4)\)y\((3,-6)\)
4. \((-5,-2)\)y\((1,-6)\)
5. \((-1,1)\)y\((-4,10)\)
6. \((8,-3)\)y\((2,-12)\)
7. \((0,-6)\)y\((-3,0)\)
8. \((0,0)\)y\((8,-4)\)
9. \(\left( \frac { 1 } { 2 } , - \frac { 1 } { 2 } \right)\)y\(\left( - 1 , \frac { 3 } { 2 } \right)\)
10. \(\left( - \frac { 1 } { 3 } , 2 \right) \)y\(\left( \frac { 5 } { 3 } , - \frac { 2 } { 3 } \right)\)

Responder

1. \(\sqrt{5}\)unidades

3. \(2\sqrt{10}\)unidades

5. \(3\sqrt{10}\)unidades

7. \(3\sqrt{5}\)unidades

9. \(\frac{5}{2}\)unidades

Ejercicio\(\PageIndex{10}\)

Determina si los tres puntos forman o no un triángulo rectángulo. Usa el teorema de Pitágoras para justificar tu respuesta.

1. \(( 2 , - 1 ) , ( - 1,2 ) , \text { and } ( 6,3 )\)
2. \(( - 5,2 ) , ( - 1 , - 2 ) , \text { and } ( - 2,5 )\)
3. \(( - 5,0 ) , ( 0,3 ) , \text { and } ( 6 , - 1 )\)
4. \(( - 4 , - 1 ) , ( - 2,5 ) , \text { and } ( 7,2 )\)
5. \(( 1 , - 2 ) , ( 2,3 ) , \text { and } ( - 3,4 )\)
6. \(( - 2,1 ) , ( - 1 , - 1 ) , \text { and } ( 1,3 )\)
7. \(( - 4,0 ) , ( - 2 , - 10 ) , \text { and } ( 3 , - 9 )\)
8. \(( 0,0 ) , ( 2,4 ) , \text { and } ( - 2,6 )\)

Responder

1. Triángulo recto

3. No es un triángulo rectángulo

5. Triángulo recto

7. Triángulo recto

Ejercicio\(\PageIndex{11}\)

1. Dar un valor para\(x\) tal que\(\sqrt { x ^ { 2 } } \neq x\). Explique por qué es importante asumir que las variables representan números no negativos.
2. Investigar y discutir los logros de Christoph Rudolff. ¿Por qué se le atribuye?
3. ¿Qué es un surd y de dónde viene la palabra?
4. Investigar formas en que los investigadores policiales puedan determinar la velocidad de un vehículo después de que se haya producido un accidente. Comparta sus hallazgos en el panel de discusión.

Responder

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

¹⁴ Una expresión algebraica que contiene radicales.

¹⁵ Dados dos puntos\((x_{1} , y_{1} )\) y\((x_{2}, y_{2})\), calcular la distancia\(d\) entre ellos usando la fórmula\(d=\sqrt { \left( x _ { 2 } - x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } - y _ { 1 } \right) ^ { 2 } }\).