7.3: Funciones logarítmicas y sus gráficas
- Page ID
- 109869
Objetivos de aprendizaje
- Definir y evaluar logaritmos.
- Identificar el logaritmo común y natural.
- Croquis de la gráfica de funciones logarítmicas.
Definición del logaritmo
Comenzamos con la función exponencial definida por\(f (x) = 2^{x}\) y notamos que pasa la prueba de línea horizontal.
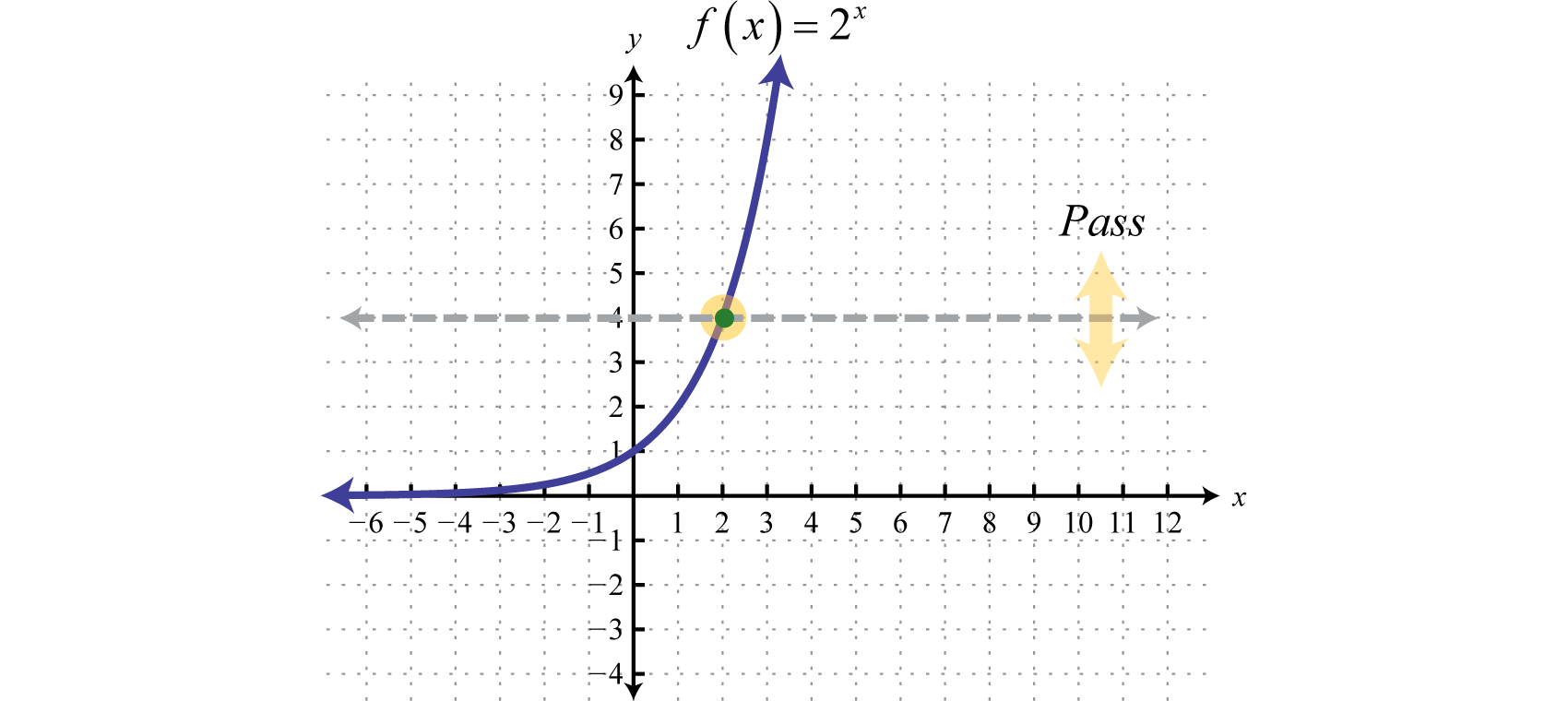
Por lo tanto es uno a uno y tiene una inversa. Reflexionando\(y = 2^{x}\) sobre la línea\(y = x\) podemos bosquejar la gráfica de su inversa. Recordemos que si\((x, y)\) es un punto en la gráfica de una función, entonces\((y, x)\) será un punto en la gráfica de su inversa.
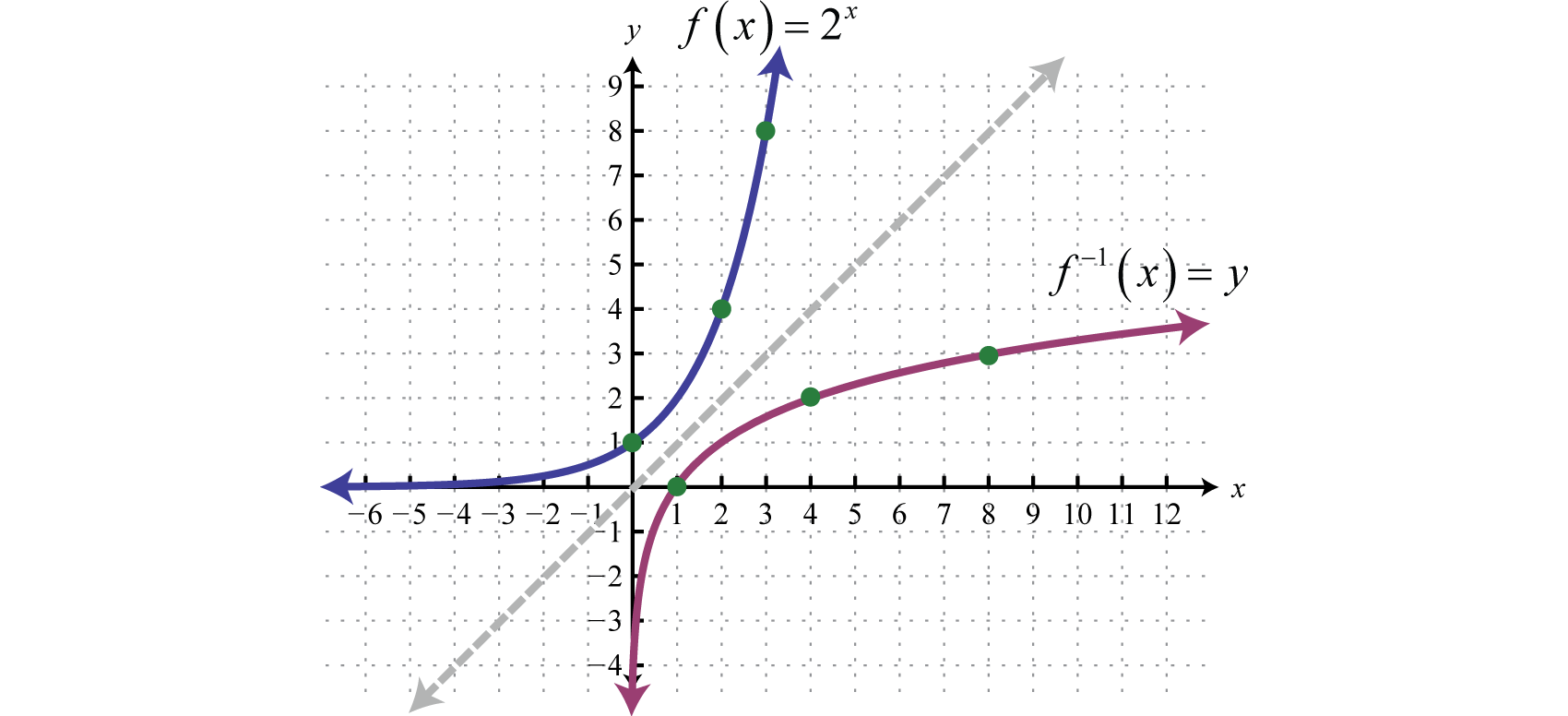
Para encontrar la inversa algebraicamente, comenzar por el\(x\) intercambio\(y\) y luego tratar de resolver para\(y\).
\(\begin{aligned} f(x) &=2^{x} \\ y &=2^{x} \quad \color{Cerulean}{\Rightarrow} \quad \color{black}{x}=2^{y} \end{aligned}\)
Rápidamente nos damos cuenta de que no hay método para resolver para\(y\). Esta función parece “trascender” el álgebra. Por lo tanto, definimos lo inverso como el\(2\) logaritmo base, denotado\(\log _{2} x\). Los siguientes son equivalentes:
\(y=\log _{2} x \color{Cerulean}{\Leftrightarrow}\color{black}{ x}=2^{y}\)
Esto nos da otra función trascendental definida por\(f^{-1}(x)=\log _{2} x\), que es la inversa de la función exponencial definida por\(f (x) = 2^{x}\).
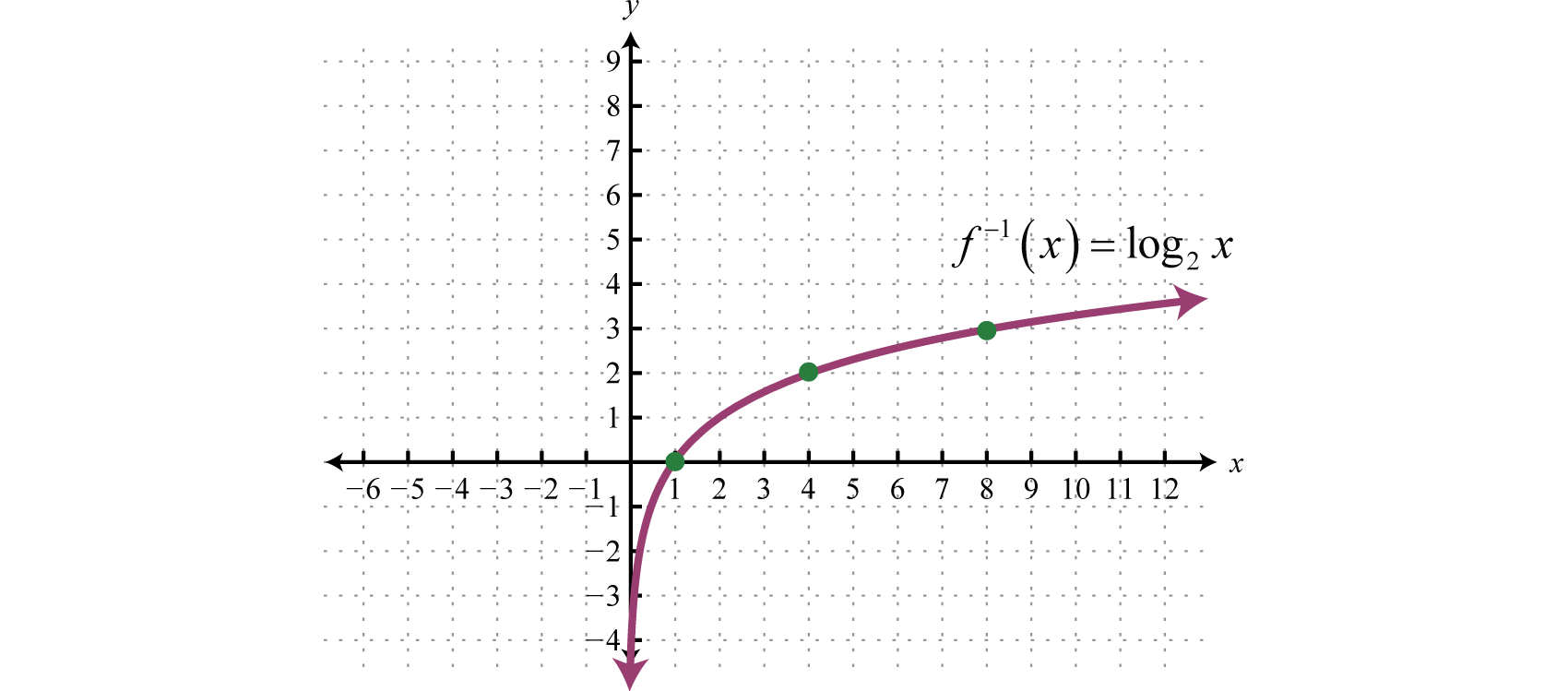
El dominio consta de todos los números reales positivos\((0, ∞)\) y el rango consiste en todos los números reales\((−∞, ∞)\). John Napier es ampliamente acreditado por haber inventado el término logaritmo.

En general, dada la base\(b > 0\) donde\(b ≠ 1\), el logaritmo base b 8 se define de la siguiente manera:
\(y=\log _{b} x\quad\color{Cerulean}{if\:and\:only\:if}\quad \color{black}{x}=b^{y}\)
Usa esta definición para convertir logaritmos a forma exponencial y espalda.
| Forma logarítmica | Forma exponencial |
|---|---|
| \(\log _{2} 16=4\) | \(2^{4}=16\) |
| \(\log _{5} 25=2\) | \(5^{2}=25\) |
| \(\log _{6} 1=0\) | \(6^{0}=1\) |
| \(\log _{3} \sqrt{3}=\frac{1}{2}\) | \(3^{1 / 2}=\sqrt{3}\) |
| \(\log _{7}\left(\frac{1}{49}\right)=-2\) | \(7^{-2}=\frac{1}{49}\) |
Es útil señalar que el logaritmo es en realidad el exponente\(y\) al que\(b\) se eleva la base para obtener el argumento\(x\).
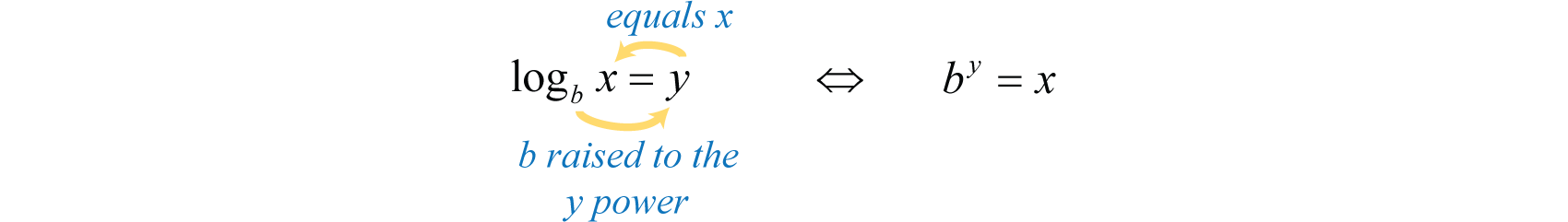
Ejemplo\(\PageIndex{1}\)
Evaluar:
- \(\log _{5} 125\)
- \(\log _{2}\left(\frac{1}{8}\right)\)
- \(\log _{4} 2\)
- \(\log _{11} 1\)
Solución
- \(\log _{5} 125=3\)porque\(5^{3}=125\).
- \(\log _{2}\left(\frac{1}{8}\right)=-3\)porque\(2^{-3}=\frac{1}{2^{3}}=\frac{1}{8}\).
- \(\log _{4} 2=\frac{1}{2}\)porque\(4^{1 / 2}=\sqrt{4}=2\).
- \(\log _{11} 1=0\)porque\(11^{0}=1\)
Tenga en cuenta que el resultado de un logaritmo puede ser negativo o incluso cero. Sin embargo, el argumento de un logaritmo no está definido para números negativos o cero:
\[\begin{aligned} \log _{2}(-4) &=\color{Cerulean}{?}\color{black}{ \Longrightarrow} 2^{\color{Cerulean}{?}} \color{black}{=} -4 \\ \log _{2}(0) &=\color{Cerulean}{?}\color{black}{\Longrightarrow}2^{\color{Cerulean}{?}}\color{black}{=}0 \end{aligned}\]
No hay poder de dos que resulte en\(−4\) o\(0\). Los números negativos y el cero no están en el dominio del logaritmo. En este punto puede ser útil volver atrás y revisar todas las reglas de los exponentes.
Ejemplo\(\PageIndex{2}\)
Encuentra\(x\):
- \(\log _{7} x=2\)
- \(\log _{16} x=\frac{1}{2}\)
- \(\log _{1 / 2} x=-5\)
Solución
Convierte cada uno a forma exponencial y luego simplifica usando las reglas de exponentes.
- \(\log _{7} x=2\)es equivalente a\(7^{2}=x\) y por lo tanto\(x=49\).
- \(\begin{array}{l}{\log _{16} x=\frac{1}{2} \text { is equivalent to } 16^{1 / 2}=x \text { or } \sqrt{16}=x \text { and thus }} {x=4 .}\end{array}\)
- \(\begin{array}{l}{\log _{1 / 2} x=-5 \text { is equivalent to }\left(\frac{1}{2}\right)^{-5}=x \text { or } 2^{5}=x \text { and thus }} {x=32}\end{array}\),
Ejercicio\(\PageIndex{1}\)
Evaluar:\(\log _{5}\left(\frac{1}{\sqrt[3]{5}}\right)\).
- Contestar
-
\(-\frac{1}{3}\)
www.youtube.com/V/1BxV8PY91BW
El logaritmo común y natural
Un logaritmo puede tener cualquier número real positivo, distinto de\(1\), como su base. Si la base es\(10\), el logaritmo se denomina logaritmo común 9.
\(f(x)=\log _{10} x=\log x\quad\color{Cerulean}{Common\:logarithm}\)
Cuando se escribe un logaritmo sin una base se supone que es el logaritmo común.
Esta convención varía con respecto al tema en el que aparece. Por ejemplo, los informáticos suelen dejar\(\log\:x\) representar la base logaritmo\(2\).
Ejemplo\(\PageIndex{3}\):
Evaluar:
- \(\log 10^{5}\)
- \(\log \sqrt{10}\)
- \(\log 0.01\)
Solución
- \(\log 10^{5}=5\)porque\(10^{5}=10^{5}\).
- \(\log \sqrt{10}=\frac{1}{2}\)porque\(10^{1 / 2}=\sqrt{10}\).
- \(\begin{array}{l}{\log 0.01=\log \left(\frac{1}{100}\right)=-2 \text { because }} {10^{-2}=\frac{1}{10^{2}}=\frac{1}{100}=0.01}\end{array}\)
El resultado de un logaritmo no siempre es aparente. Por ejemplo, considere\(log\:75\).
\(\begin{aligned} \log 10&=1 \\ \log 75&= \color{Cerulean}{?} \\ \log 100&=2 \end{aligned}\)
Podemos ver que el resultado de\(log\:75\) está en algún lugar entre\(1\) y\(2\). En la mayoría de las calculadoras científicas hay un botón logaritmo común LOG.Utilízalo para encontrar lo\(log\:75\) siguiente:
\(LOG\:75=1.87506\)
Por lo tanto, redondeado a la milésima más cercana,\(log\:75 ≈ 1.875\). Como cheque, podemos usar una calculadora para verificar eso\(10^{\wedge} 1.875 \approx 75\).
Si la base de un logaritmo es\(e\), el logaritmo se denomina logaritmo natural 10.
\(f(x)=\log _{e} x=\ln x\quad\color{Cerulean}{Natural\:logarithm}\)
El logaritmo natural es ampliamente utilizado y a menudo se abrevía\(ln\:x\).
Ejemplo\(\PageIndex{4}\)
Evaluar:
- \(\ln e\)
- \(\ln \sqrt[3]{e^{2}}\)
- \(\ln \left(\frac{1}{e^{4}}\right)\)
Solución
- \(\ln e=1 \text { because } \ln e=\log _{e} e=1 \text { and } e^{1}=e\).
- \(\ln \left(\sqrt[3]{e^{2}}\right)=\frac{2}{3}\)porque\(e^{2 / 3}=\sqrt[3]{e^{2}}\).
- \(\ln \left(\frac{1}{e^{4}}\right)=-4\)porque\(e^{-4}=\frac{1}{e^{4}}\).
En una calculadora encontrarás un botón para el logaritmo natural LN.
\(LN\:75\:=\:4.317488\)
Por lo tanto, redondeado a la milésima más cercana,\(ln\:(75) ≈ 4.317\). Como cheque, podemos usar una calculadora para verificar eso\(e^{\wedge} 4.317 \approx 75\).
Ejemplo\(\PageIndex{5}\)
Encontrar\(x\). Respuestas redondas a la milésima más cercana.
- \(\log x=3.2\)
- \(\ln x=-4\)
- \(\log x=-\frac{2}{3}\)
Solución
Convierte cada uno a forma exponencial y luego usa una calculadora para aproximar la respuesta.
- \(\log x=3.2\)es equivalente a\(10^{3.2}=x\) y por lo tanto\(x \approx 1584.893\).
- \(\ln x=-4\)es equivalente a\(e^{-4}=x\) y por lo tanto\(x \approx 0.018\).
- \(\log x=-\frac{2}{3}\)es equivalente a\(10^{-2 / 3}=x\) y por lo tanto\(x \approx 0.215\).
Ejercicio\(\PageIndex{2}\)
Evaluar:\(\ln \left(\frac{1}{\sqrt{e}}\right)\)
- Contestar
-
\(-frac{1}{2}\)
www.youtube.com/v/flw7_zv7qme
Graficar funciones logarítmicas
Podemos usar las traducciones para graficar funciones logarítmicas. Cuando la base\(b > 1\), la gráfica de\(f (x) = log_{b}x\) tiene la siguiente forma general:
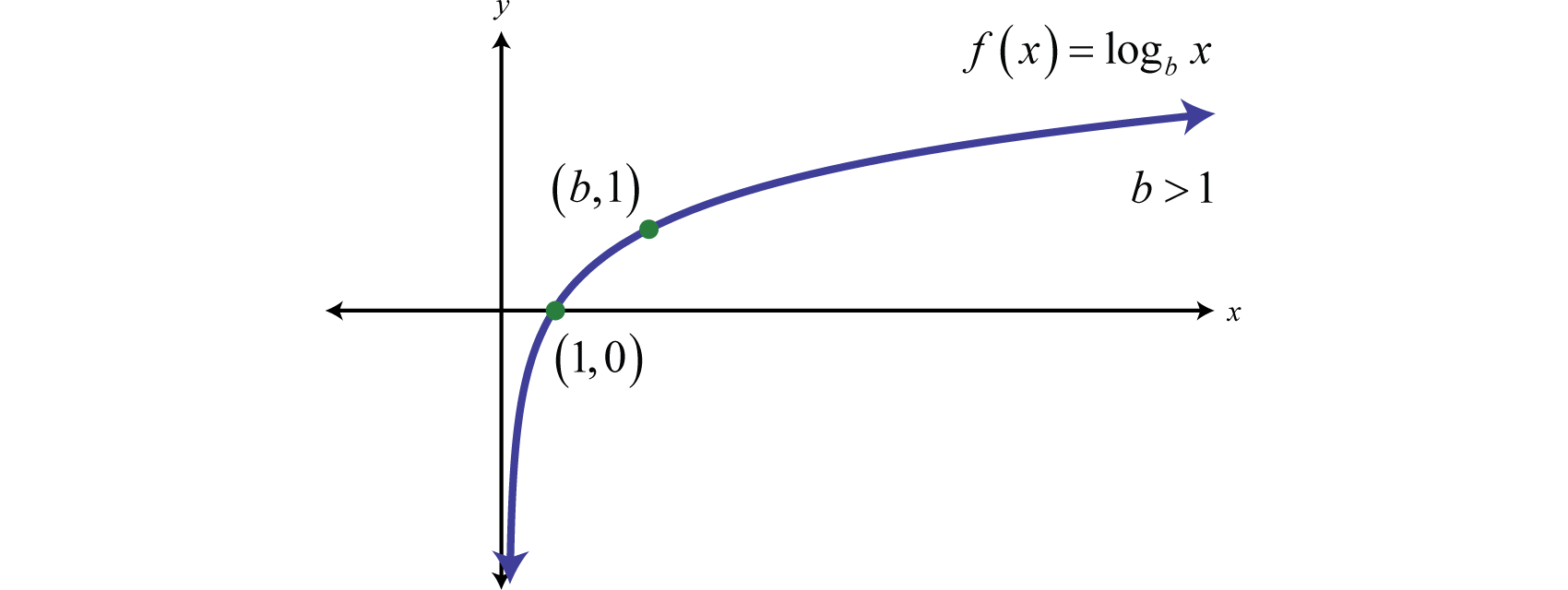
El dominio consiste en números reales positivos,\((0, ∞)\) y el rango consiste en todos los números reales,\((−∞, ∞)\). El\(y\) -eje, o\(x = 0\), es una asíntota vertical y la\(x\) -intercepción es\((1, 0)\). Además,\(f (b) = log_{b}b = 1\) y así lo\((b, 1)\) es un punto en la gráfica sin importar cuál sea la base.
Ejemplo\(\PageIndex{6}\)
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=\log _{3}(x+4)-1\).
Solución
Comience por identificar la gráfica básica y las transformaciones.
\(\begin{array}{l}{y=\log _{3} x}\quad\quad\quad\quad\:\:\:\:\color{Cerulean}{Basic\:graph.} \\ {y=\log _{3}(x+4)}\quad\quad\:\:\color{Cerulean}{Shift\:left\:4\:units.} \\ {y=\log _{3}(x+4)-1}\:\:\:\color{Cerulean}{Shift\:down\:1\:unit.}\end{array}\)
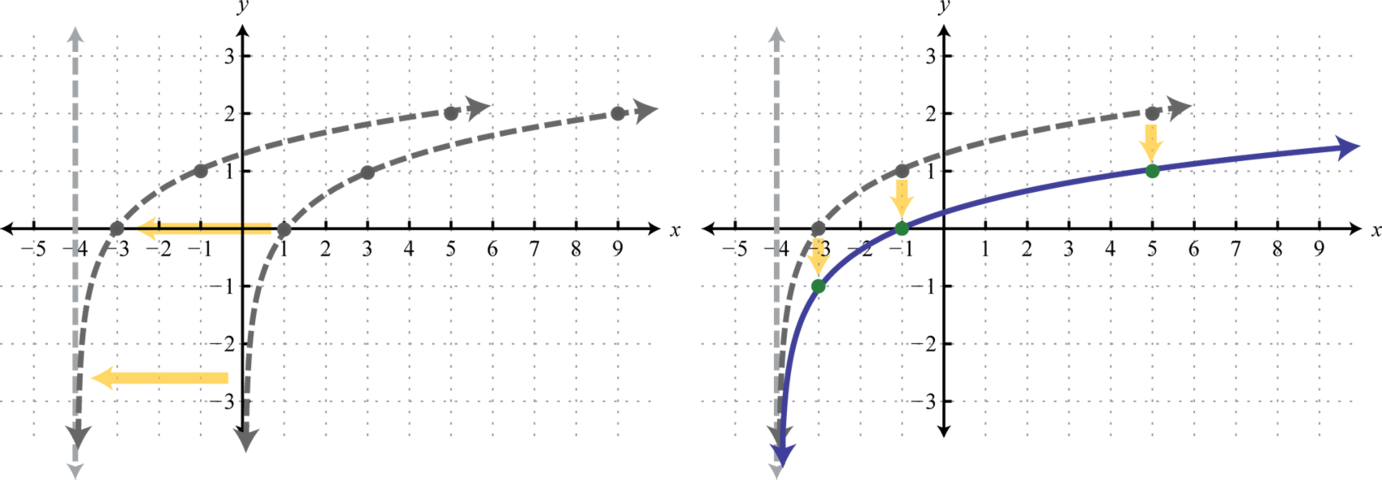
Observe que la asíntota también se desplazó\(4\) unidades hacia la izquierda. Esto define el límite inferior del dominio. La gráfica final se presenta sin los pasos intermedios.
Respuesta:
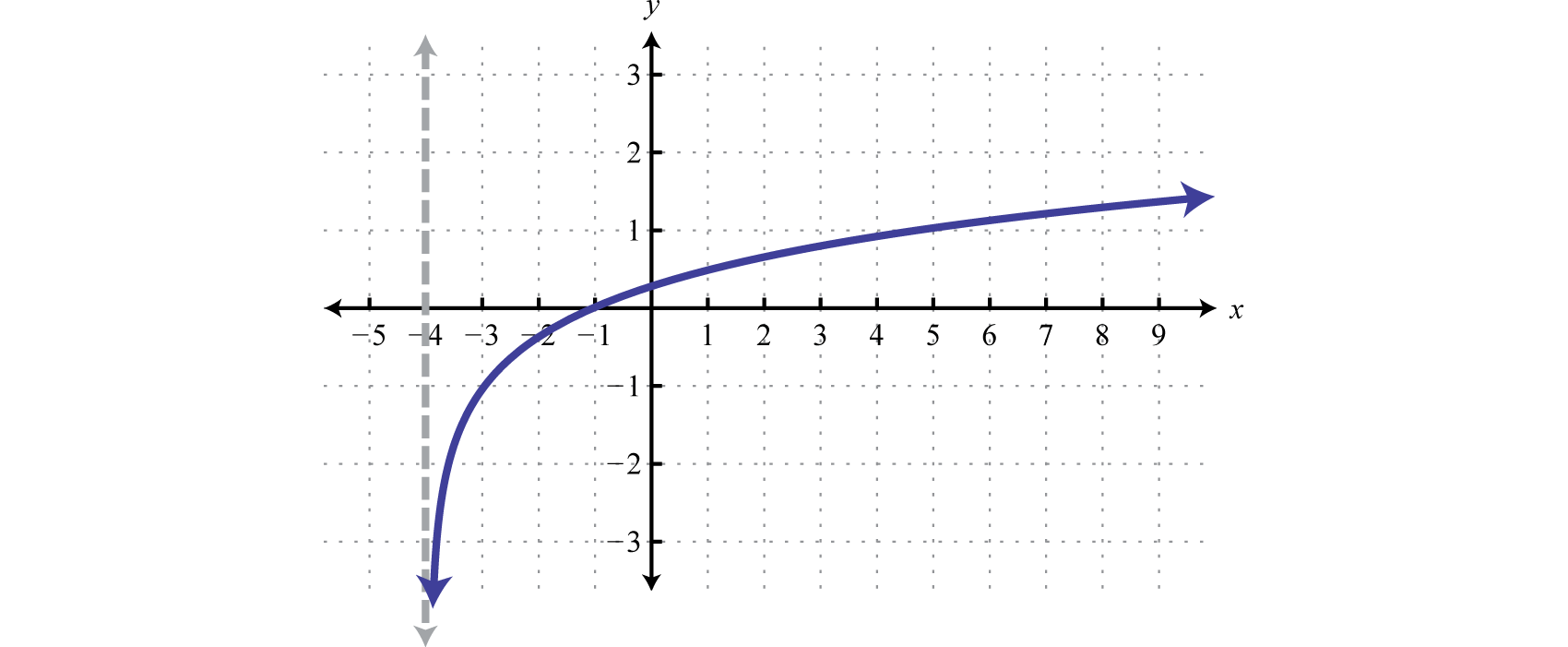
Dominio:\((-4, \infty)\); Rango:\((-\infty, \infty)\)
Encontrar las intercepciones de la gráfica en el ejemplo anterior se deja para una sección posterior en este capítulo. Por ahora, nos preocupa más la forma general de las funciones logarítmicas.
Ejemplo\(\PageIndex{7}\)
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=-\log (x-2)\).
Solución
Comience por identificar la gráfica básica y las transformaciones.
\(\begin{array}{l}{y=\log x}\quad\quad\quad\quad\color{Cerulean}{Basic\:graph.} \\ {y=-\log x}\quad\quad\quad\color{Cerulean}{Reflection\:about\:the\:x-axis.} \\ {y=-\log (x-2)}\:\:\:\color{Cerulean}{Shift\:right\:2\:units.}\end{array}\)
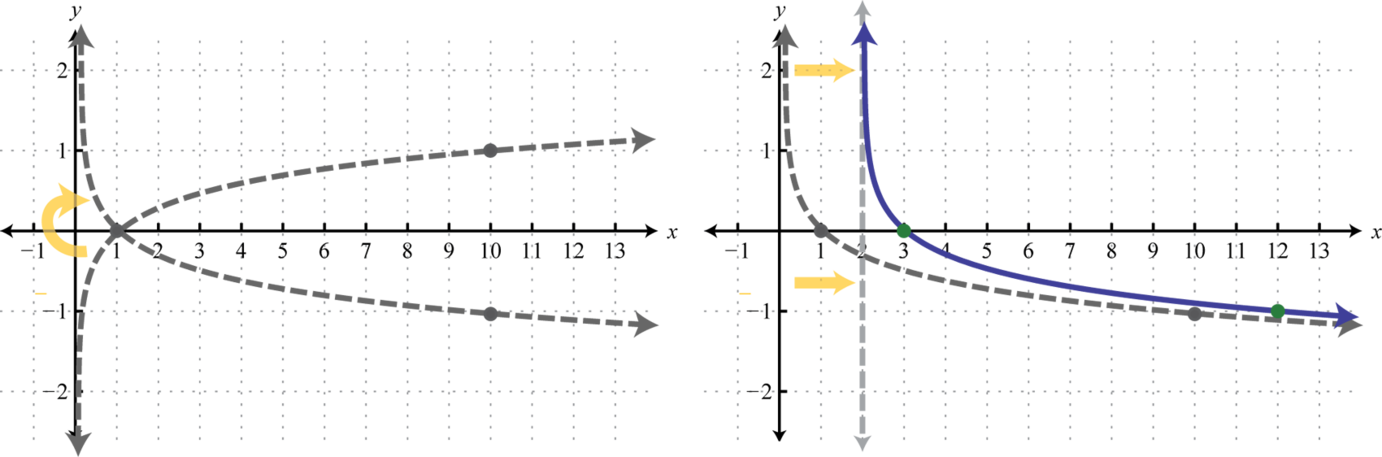
Aquí la asíntota vertical se desplazó dos unidades hacia la derecha. Esto define el límite inferior del dominio.
Contestar
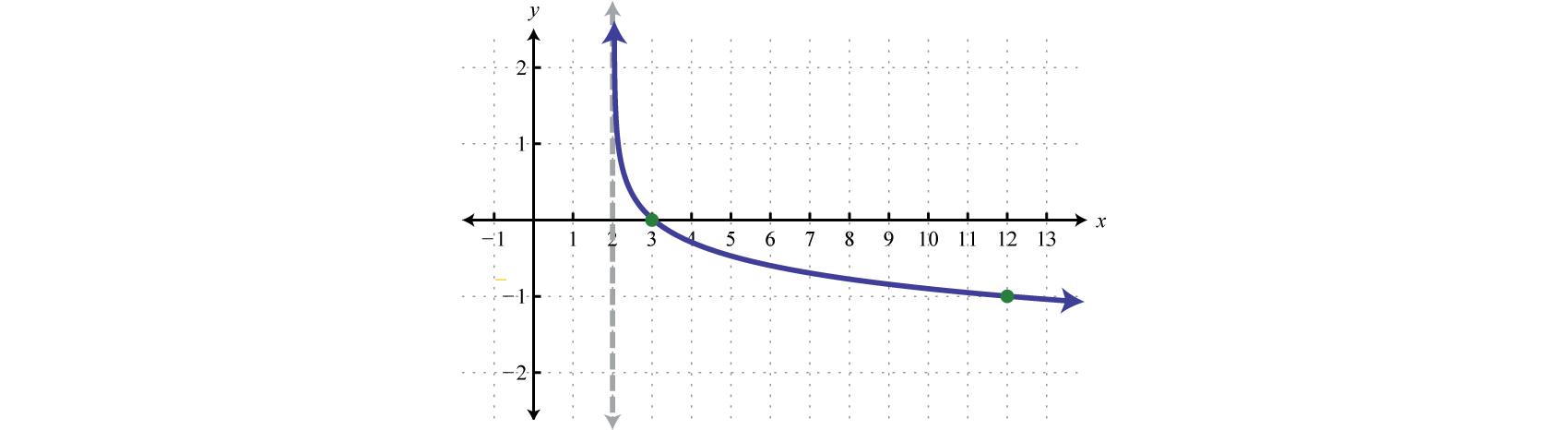
Dominio:\((2, \infty)\); Rango:\((-\infty, \infty)\)
Ejercicio\(\PageIndex{3}\)
Dibuje la gráfica y determine el dominio y el rango:\(g(x)=\ln (-x)+2\).
- Contestar
-
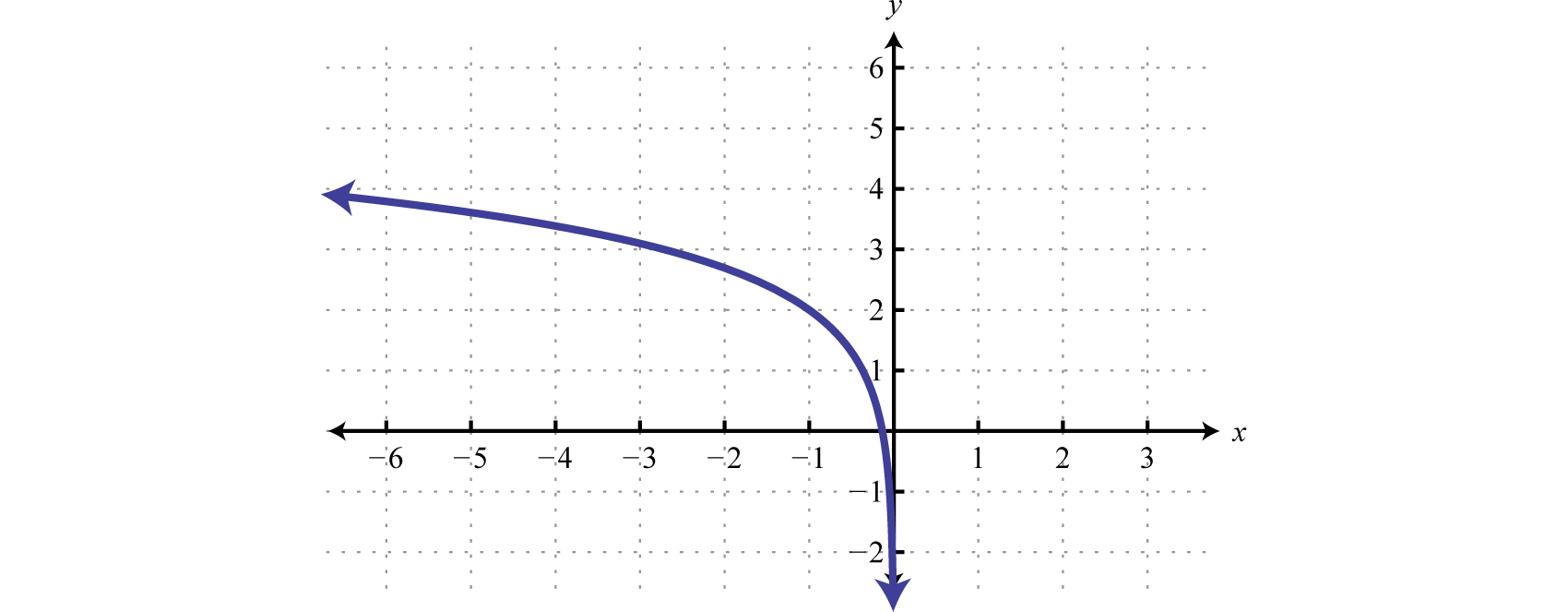
Figura\(\PageIndex{11}\) Dominio:\((-\infty, 0)\); Rango:\((-\infty, \infty)\)
www.youtube.com/v/6obhbjfcde4
A continuación, considere funciones exponenciales con bases fraccionarias, como la función definida por\(f (x) = (\frac{1}{2})^{x}\). El dominio consta de todos los números reales. Elija algunos valores para\(x\) y luego encuentre los\(y\) valores -correspondientes.
| \(x\) | \(y\) | \(\color{Cerulean}{Solutions} \) | |
|---|---|---|---|
| \ (x\) ">\(-2\) | \ (y\) ">\(\color{Cerulean}{4} \) | \(f(-2)=\left(\frac{1}{2}\right)^{-2}=2^{2}=4\) | \ (\ color {cerúleo} {Soluciones}\) ">\((-2,4)\) |
| \ (x\) ">\(-1\) | \ (y\) ">\(\color{Cerulean}{2}\) | \(f(-1)=\left(\frac{1}{2}\right)^{-1}=2^{1}=2\) | \ (\ color {cerúleo} {Soluciones}\) ">\((-1,2)\) |
| \ (x\) ">\(0\) | \ (y\) ">\(\color{Cerulean}{1}\) | \(f(0)=\left(\frac{1}{2}\right)^{0}=1\) | \ (\ color {cerúleo} {Soluciones}\) ">\((0,1)\) |
| \ (x\) ">\(1\) | \ (y\) ">\(\color{Cerulean}{\frac{1}{2}}\) | \(f(1)=\left(\frac{1}{2}\right)^{1}=\frac{1}{2}\) | \ (\ color {cerúleo} {Soluciones}\) ">\(\left(1, \frac{1}{2}\right)\) |
| \ (x\) ">\(2\) | \ (y\) ">\(\color{Cerulean}{\frac{1}{4}}\) | \(f(2)=\left(\frac{1}{2}\right)^{2}=\frac{1}{4}\) | \ (\ color {cerúleo} {Soluciones}\) ">\(\left(2, \frac{1}{4}\right)\) |
Utilice estos puntos para bosquejar la gráfica y tenga en cuenta que pasa la prueba de línea horizontal.
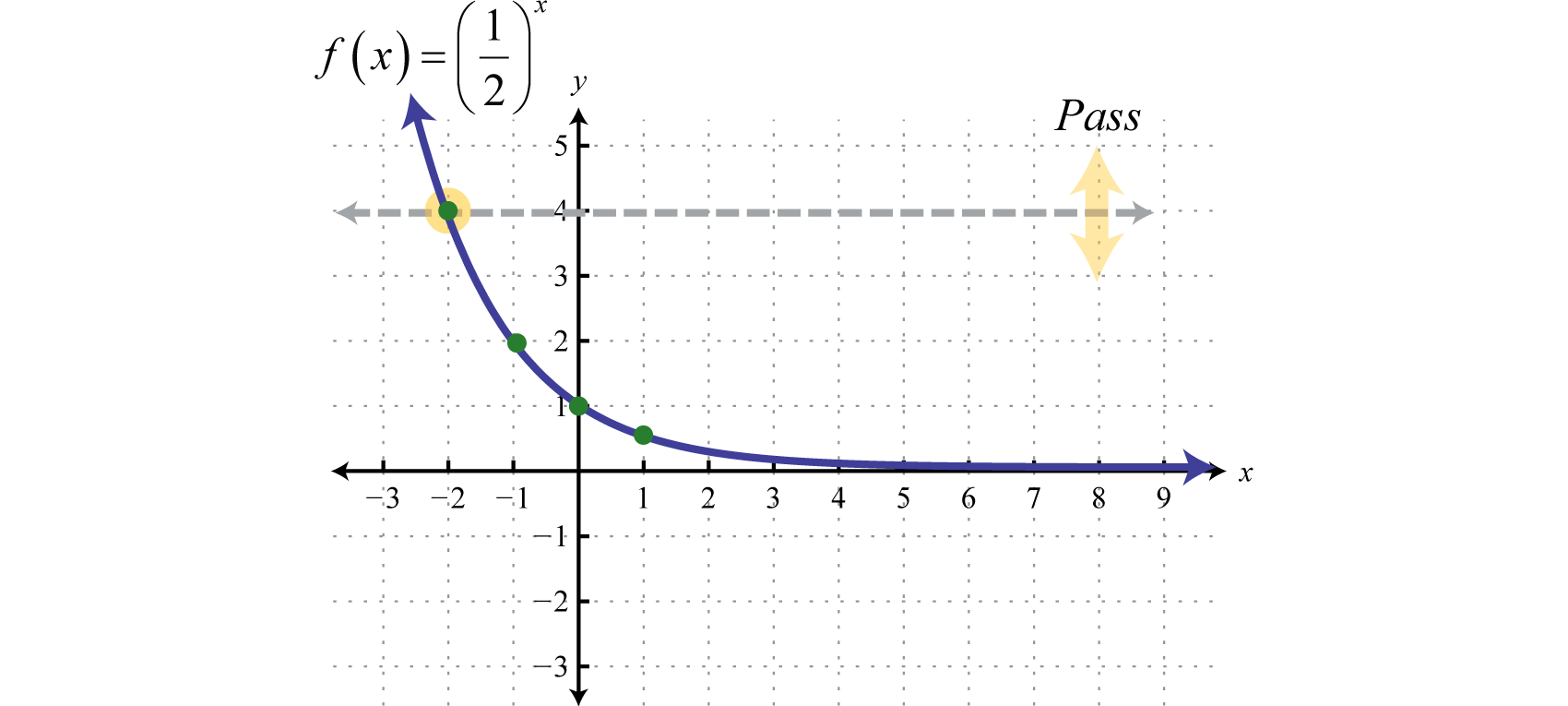
Por lo tanto esta función es uno a uno y tiene una inversa. Reflejando la gráfica sobre la línea\(y = x\) tenemos:
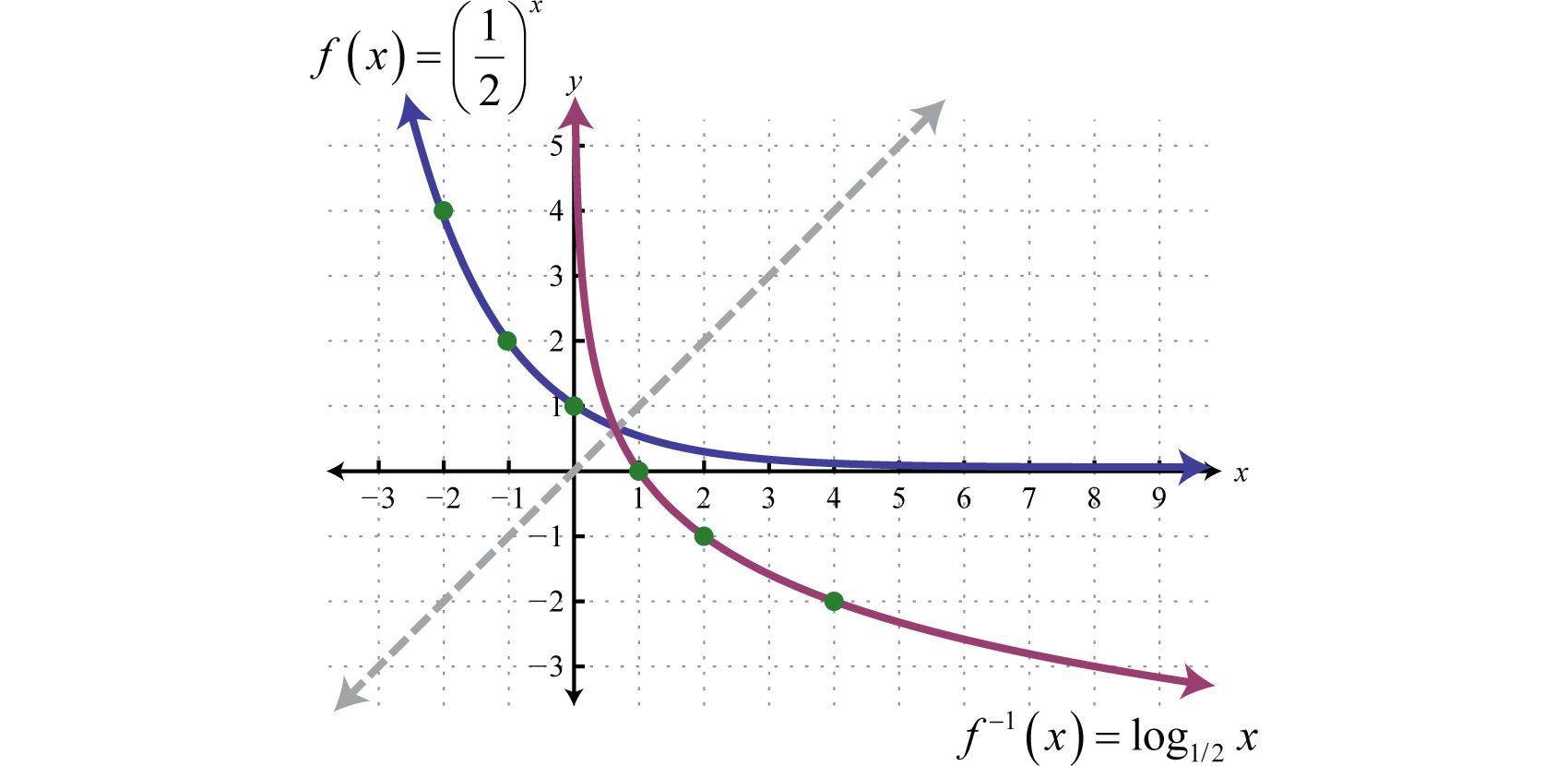
lo que nos da una imagen de la gráfica de\(f^{-1}(x)=\log _{1 / 2} x\). En general, cuando la base\(b > 1\), la gráfica de la función definida por\(g(x)=\log _{1 / b} x\) tiene la siguiente forma.
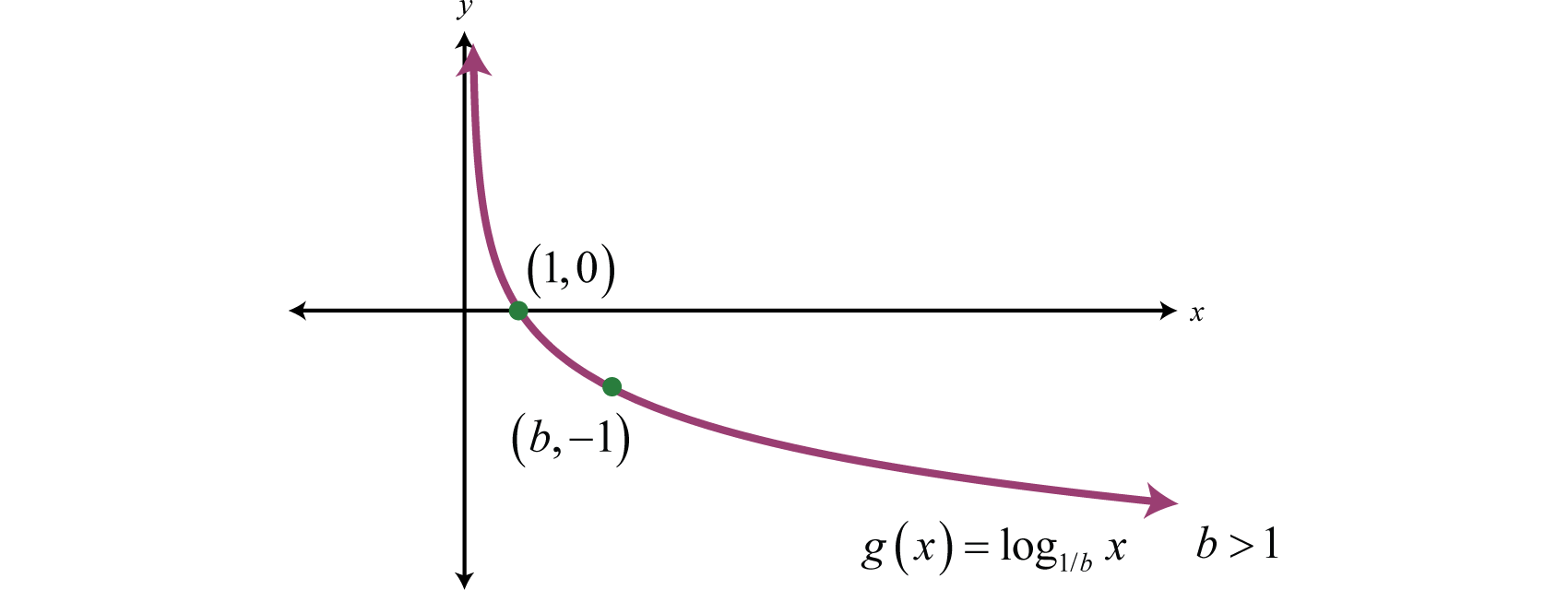
El dominio consiste en números reales positivos,\((0, ∞)\) y el rango consiste en todos los números reales,\((−∞, ∞)\). El\(y\) -eje, o\(x = 0\), es una asíntota vertical y la\(x\) -intercepción es\((1, 0)\). Además,\(f(b)=\log _{1 / b} b=-1\) y así lo\((b, −1)\) es un punto en la gráfica.
Ejemplo\(\PageIndex{8}\):
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=\log _{1 / 3}(x+3)+2\).
Solución
Comience por identificar la gráfica básica y las transformaciones.
\[\begin{array}{l}{y=\log _{1 / 3} x}\quad\quad\quad\quad\:\:\:\:\color{Cerulean}{Basic\:graph.} \\ {y=\log _{1 / 3}(x+3)}\quad\quad\:\:\color{Cerulean}{Shift\:left\:3\:units.} \\ {y=\log _{1 / 3}(x+3)+2}\:\:\:\color{Cerulean}{Shift\:up\:2\:units.}\end{array}\]
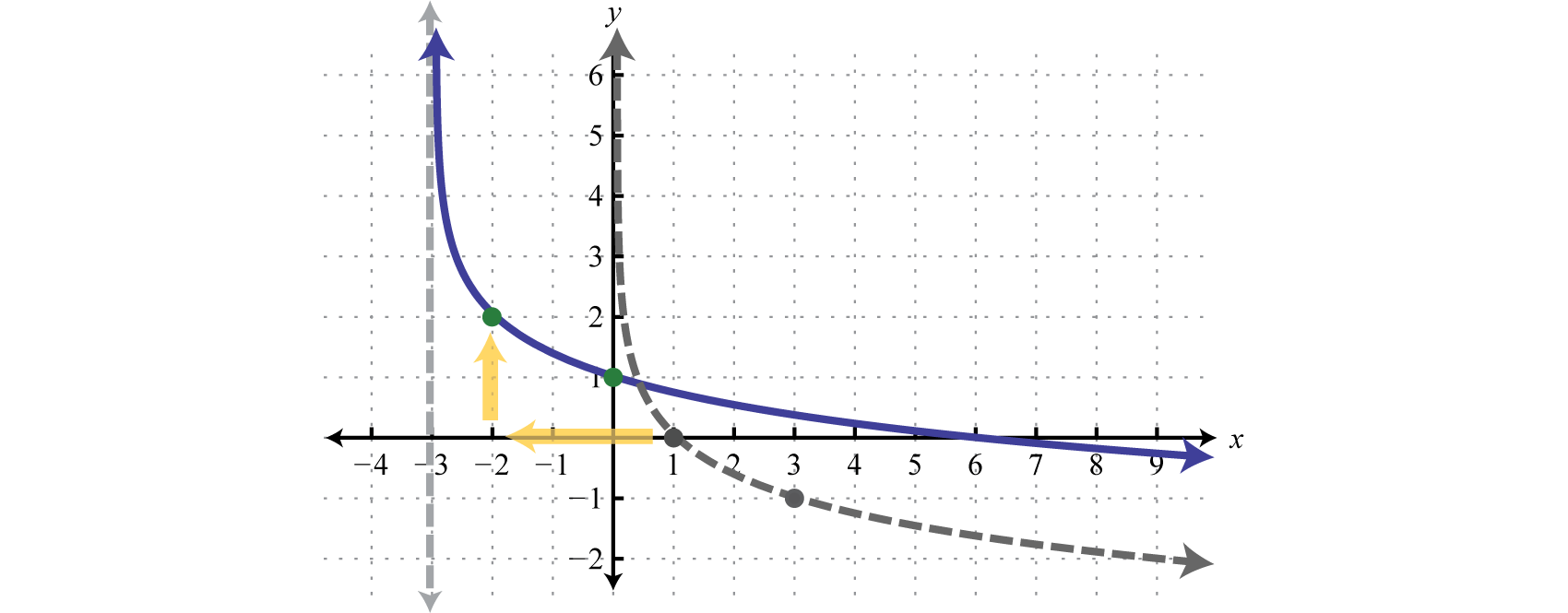
En este caso las\(3\) unidades de desplazamiento a la izquierda movieron la asíntota vertical a la\(x = −3\) que define el límite inferior del dominio.
Respuesta:
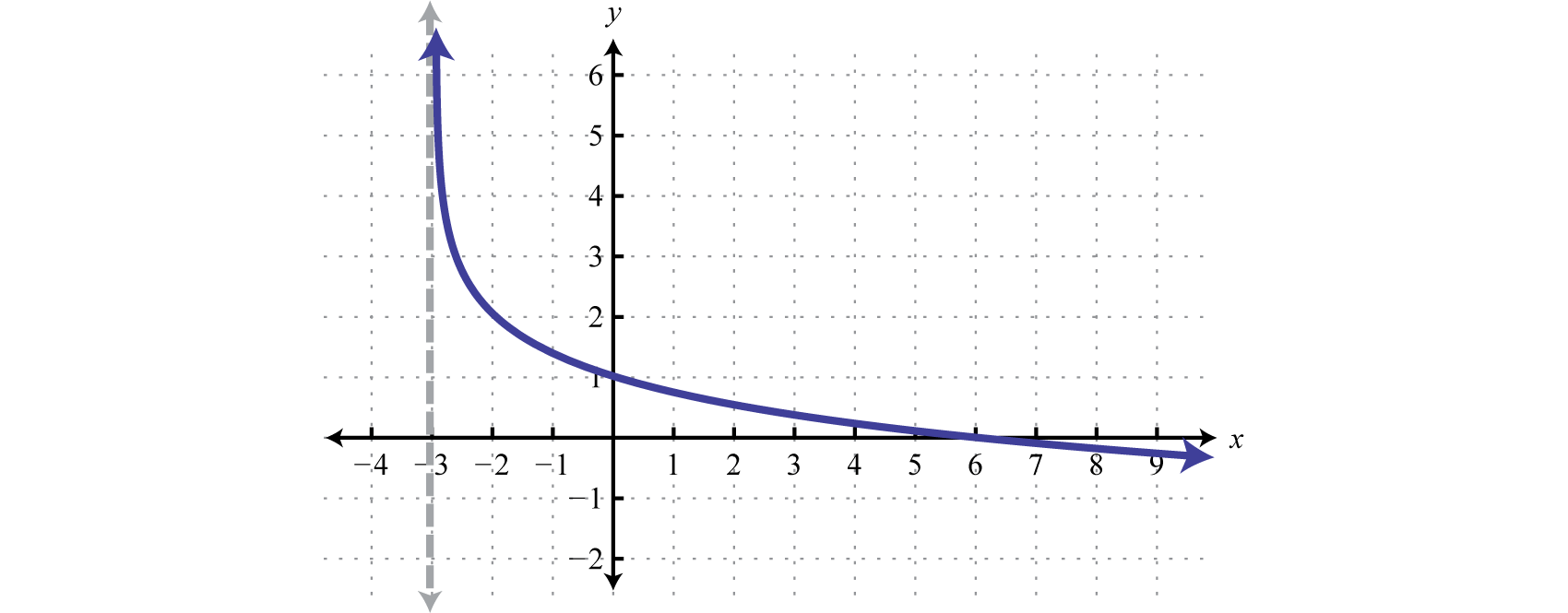
Dominio:\((-3, \infty)\); Rango:\((-\infty, \infty)\)
En resumen, si\(b>1\)
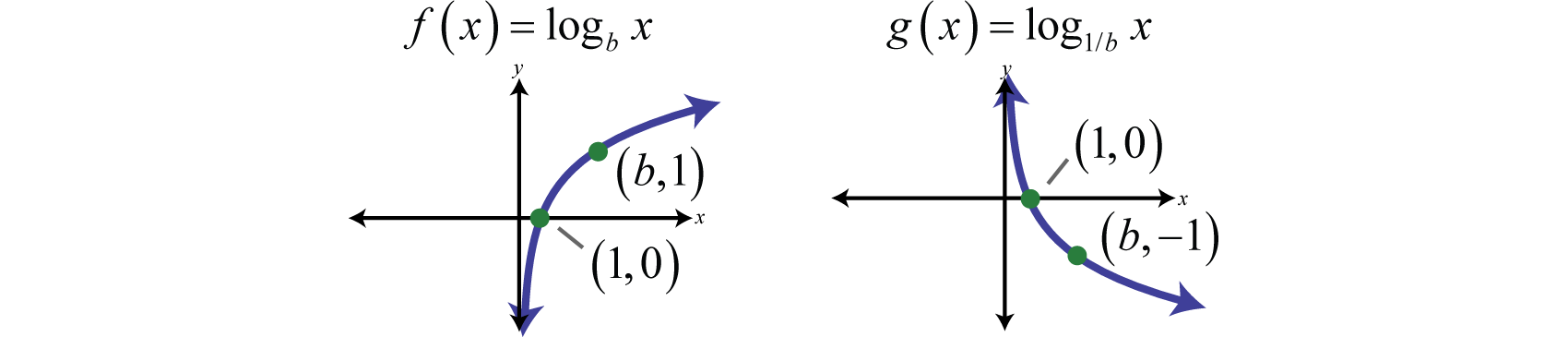
Y para ambos casos,
\[\begin{aligned} \color{Cerulean} { Domain: }&\color{black}{(}0, \infty) \\ \color{Cerulean} { Range: }&\color{black}{(}-\infty, \infty) \\ \color{Cerulean} { x-intercept: }&\color{black}{(}1,0) \\ \color{Cerulean} { Asymptote: }& \color{black}{x}=0 \end{aligned}\]
Ejercicio\(\PageIndex{4}\)
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=\log _{1 / 3}(x-1)\).
- Contestar
-
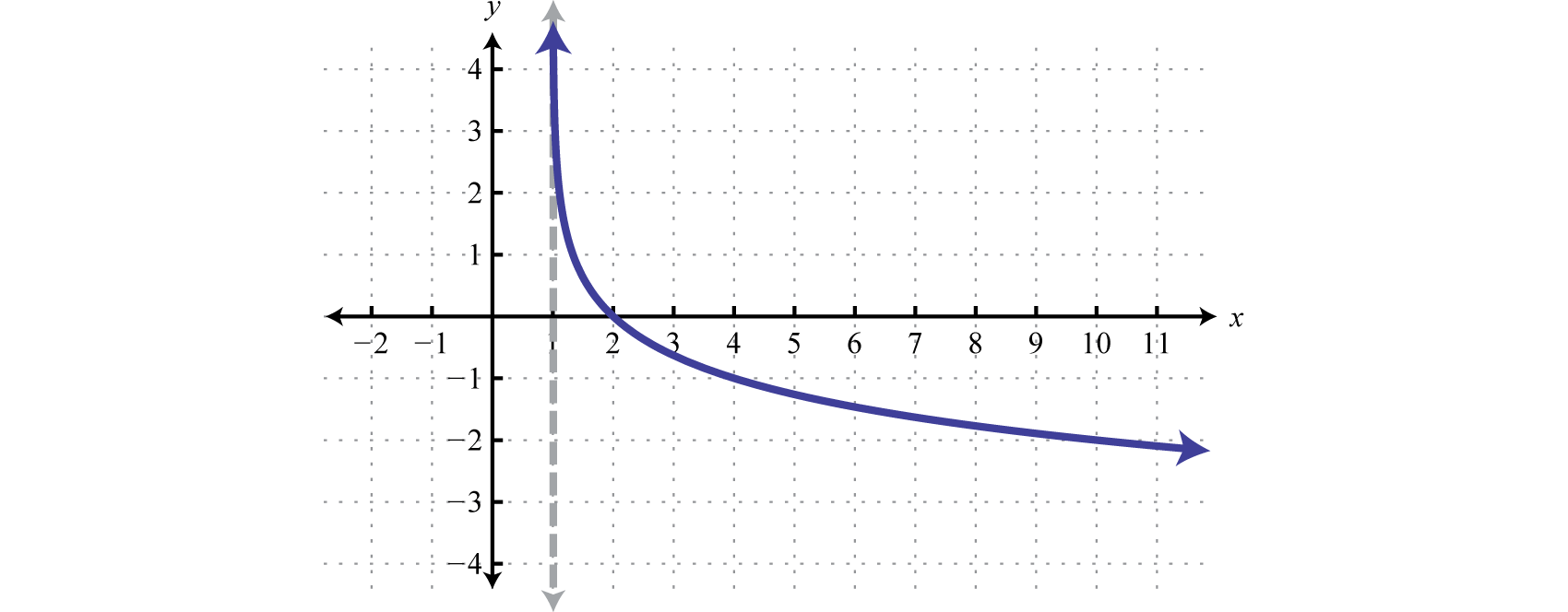
Figura\(\PageIndex{18}\) www.youtube.com/v/0oevfincaxw
Claves para llevar
- La función\(b\) logarítmica base se define como la inversa de la función\(b\) base-exponencial. En otras palabras,\(y = \log_{b}x\) si y sólo si\(b^{y} = x\) donde\(b > 0\) y\(b ≠ 1\).
- El logaritmo es en realidad el exponente al que se eleva la base para obtener su argumento.
- La base logaritmo\(10\) se denomina logaritmo común y se denota\(\log\:x\).
- La base logaritmo\(e\) se llama logaritmo natural y se denota\(\ln\:x\).
- Las funciones logarítmicas con definiciones de la forma\(f (x) = \log_{b}x\) tienen un dominio que consiste en números reales positivos\((0, ∞)\) y un rango que consiste en todos los números reales\((−∞, ∞)\).
- El\(y\) -eje, o\(x = 0\), es una asíntota vertical y la\(x\) -intercepción es\((1, 0)\).
- Para graficar funciones logarítmicas podemos trazar puntos o identificar la función básica y usar las transformaciones. Asegúrese de indicar que hay una asíntota vertical usando una línea discontinua. Esta asíntota define el límite del dominio.
Ejercicio\(\PageIndex{5}\)
Evaluar.
- \(\log _{3} 9\)
- \(\log _{7} 49\)
- \(\log _{4} 4\)
- \(\log _{5} 1\)
- \(\log _{5} 625\)
- \(\log _{3} 243\)
- \(\log _{2}\left(\frac{1}{16}\right)\)
- \(\log _{3}\left(\frac{1}{9}\right)\)
- \(\log _{5}\left(\frac{1}{125}\right)\)
- \(\log _{2}\left(\frac{1}{64}\right)\)
- \(\log _{4} 4^{10}\)
- \(\log _{9} 9^{5}\)
- \(\log _{5} \sqrt[3]{5}\)
- \(\log _{2} \sqrt{2}\)
- \(\log _{7}\left(\frac{1}{\sqrt{7}}\right)\)
- \(\log _{9}\left(\frac{1}{\sqrt[3]{9}}\right)\)
- \(\log _{1 / 2} 4\)
- \(\log _{1 / 3} 27\)
- \(\log _{2 / 3}\left(\frac{2}{3}\right)\)
- \(\log _{3 / 4}\left(\frac{9}{16}\right)\)
- \(\log _{25} 5\)
- \(\log _{8} 2\)
- \(\log _{4}\left(\frac{1}{2}\right)\)
- \(\log _{27}\left(\frac{1}{3}\right)\)
- \(\log _{1 / 9} 1\)
- \(\log _{3 / 5}\left(\frac{5}{3}\right)\)
- Contestar
-
1. \(2\)
3. \(1\)
5. \(4\)
7. \(−4\)
9. \(−3\)
11. \(10\)
13. \(\frac{1}{3}\)
15. \(−\frac{1}{2}\)
17. \(−2\)
19. \(1\)
21. \(\frac{1}{2}\)
23. \(−\frac{1}{2}\)
25. \(0\)
Ejercicio\(\PageIndex{6}\)
Encontrar\(x\).
- \(\log _{3} x=4\)
- \(\log _{2} x=5\)
- \(\log _{5} x=-3\)
- \(\log _{6} x=-2\)
- \(\log _{12} x=0\)
- \(\log _{7} x=-1\)
- \(\log _{1 / 4} x=-2\)
- \(\log _{2 / 5} x=2\)
- \(\log _{1 / 9} x=\frac{1}{2}\)
- \(\log _{1 / 4} x=\frac{3}{2}\)
- \(\log _{1 / 3} x=-1\)
- \(\log _{1 / 5} x=0\)
- Contestar
-
1. \(81\)
3. \(\frac{1}{125}\)
5. \(1\)
7. \(16\)
9. \(\frac{1}{3}\)
11. \(3\)
Ejercicio\(\PageIndex{7}\)
Evaluar. Redondear a la centésima más cercana en su caso.
- \(\log 1000\)
- \(\log 100\)
- \(\log 0.1\)
- \(\log 0.0001\)
- \(\log 162\)
- \(\log 23\)
- \(\log 0.025\)
- \(\log 0.235\)
- \(\ln e^{4}\)
- \(\ln 1\)
- \(\ln \left(\frac{1}{e}\right)\)
- \(\ln \left(\frac{1}{e^{5}}\right)\)
- \(\ln (25)\)
- \(\ln (100)\)
- \(\ln (0.125)\)
- \(\ln (0.001)\)
- Contestar
-
1. \(3\)
3. \(−1\)
5. \(2.21\)
7. \(−1.60\)
9. \(4\)
11. \(−1\)
13. \(3.22\)
15. \(−2.08\)
Ejercicio\(\PageIndex{8}\)
Encontrar\(x\). Redondear a la centésima más cercana.
- \(\log x=2.5\)
- \(\log x=1.8\)
- \(\log x=-1.22\)
- \(\log x=-0.8\)
- \(\ln x=3.1\)
- \(\ln x=1.01\)
- \(\ln x=-0.69\)
- \(\ln x=-1\)
- Contestar
-
1. \(316.23\)
3. \(0.06\)
5. \(22.20\)
7. \(0.50\)
Ejercicio\(\PageIndex{9}\)
Encuentra\(a\) sin usar una calculadora.
- \(\log _{3}\left(\frac{1}{27}\right)=a\)
- \(\ln e=a\)
- \(\log _{2} a=8\)
- \(\log _{2} \sqrt[5]{2}=a\)
- \(\log 10^{12}=a\)
- \(\ln a=9\)
- \(\log _{1 / 8}\left(\frac{1}{64}\right)=a\)
- \(\log _{6} a=-3\)
- \(\ln a=\frac{1}{5}\)
- \(\log _{4/9}\left(\frac{2}{3}\right)=a\)
- Contestar
-
1. \(−3\)
3. \(256\)
5. \(12\)
7. \(2\)
9. \(\sqrt[5]{e}\)
Ejercicio\(\PageIndex{10}\)
En 1935 Charles Richter desarrolló una escala utilizada para medir sismos en un sismógrafo. La magnitud\(M\) de un sismo viene dada por la fórmula,
\(M=\log \left(\frac{I}{I_{0}}\right)\)
Aquí\(I\) representa la intensidad del sismo medida en el sismógrafo\(100\) a km del epicentro y\(I_{0}\) es la intensidad mínima utilizada para la comparación. Por ejemplo, si la intensidad de un sismo se mide para que sea\(100\) multiplicada por la mínima, entonces\(I = 100I_{0}\) y
\(M=\log \left(\frac{100 I_{0}}{I_{0}}\right)=\log (100)=2\)
Se diría que el sismo tiene una magnitud\(2\) en la escala de Richter. Determinar las magnitudes de las siguientes intensidades en la escala de Richter. Redondear a la décima más cercana.
- \(I\)es\(3\) millones de veces la de la intensidad mínima.
- \(I\)es\(6\) millones de veces la de la intensidad mínima.
- \(I\)es la misma que la intensidad mínima.
- \(I\)es\(30\) millones de veces la de la intensidad mínima.
- Contestar
-
1. \(6.5\)
3. \(0\)
Ejercicio\(\PageIndex{11}\)
En química, el pH es una medida de acidez y viene dado por la fórmula,
\(\mathrm{pH}=-\log \left(H^{+}\right)\)
Aquí\(H^{+}\) representa la concentración de iones hidrógeno (medida en moles de hidrógeno por litro de solución). Determinar el pH dadas las siguientes concentraciones de iones hidrógeno.
- Agua pura:\(H^{+}=0.0000001\)
- Arándano:\(H^{+}=0.0003162\)
- Zumo de limón:\(H^{+}=0.01\)
- Ácido de la batería:\(H^{+}=0.1\)
- Contestar
-
1. \(7\)
3. \(2\)
Ejercicio\(\PageIndex{12}\)
Esbozar la función y determinar el dominio y el rango. Dibuja la asíntota vertical con una línea discontinua.
- \(f(x)=\log _{2}(x+1)\)
- \(f(x)=\log _{3}(x-2)\)
- \(f(x)=\log _{2} x-2\)
- \(f(x)=\log _{3} x+3\)
- \(f(x)=\log _{2}(x-2)+4\)
- \(f(x)=\log _{3}(x+1)-2\)
- \(f(x)=-\log _{2} x+1\)
- \(f(x)=-\log _{3}(x+3)\)
- \(f(x)=\log _{2}(-x)+1\)
- \(f(x)=2-\log _{3}(-x)\)
- \(f(x)=\log x+5\)
- \(f(x)=\log x-1\)
- \(f(x)=\log (x+4)-8\)
- \(f(x)=\log (x-5)+10\)
- \(f(x)=-\log (x+2)\)
- \(f(x)=-\log (x-1)+2\)
- \(f(x)=\ln (x-3)\)
- \(f(x)=\ln x+3\)
- \(f(x)=\ln (x-2)+4\)
- \(f(x)=\ln (x+5)\)
- \(f(x)=2-\ln x\)
- \(f(x)=-\ln (x-1)\)
- \(f(x)=\log _{1 / 2} x\)
- \(f(x)=\log _{1 / 3} x+2\)
- \(f(x)=\log _{1 / 2}(x-2)\)
- \(f(x)=\log _{1 / 3}(x+1)-1\)
- \(f(x)=2-\log _{1 / 4} x\)
- \(f(x)=1+\log _{1 / 4}(-x)\)
- \(f(x)=1-\log _{1 / 3}(x-2)\)
- \(f(x)=1+\log _{1 / 2}(-x)\)
- Contestar
-
1. Dominio:\((−1, ∞)\); Rango:\((−∞, ∞)\)
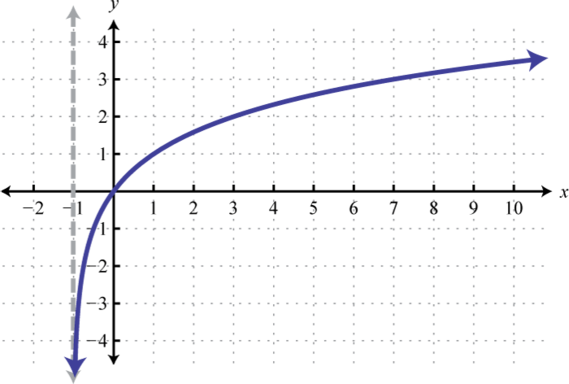
Figura\(\PageIndex{19}\) 3. Dominio:\((0, ∞)\); Rango:\((−∞, ∞)\)
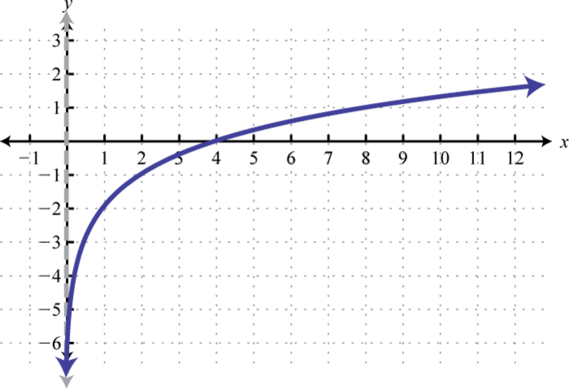
Figura\(\PageIndex{20}\) 5. Dominio:\((2, ∞)\); Rango:\((−∞, ∞)\)
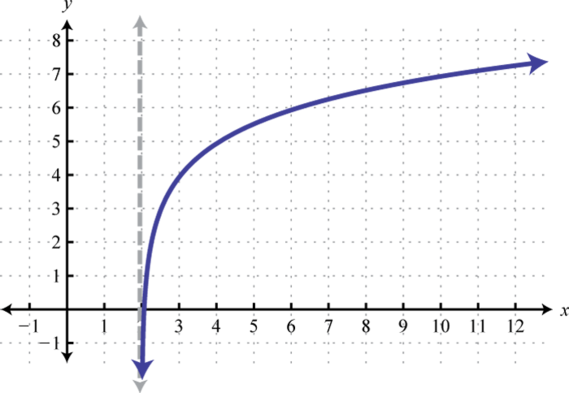
Figura\(\PageIndex{21}\) 7. Dominio:\((0, ∞)\); Rango:\((−∞, ∞)\)
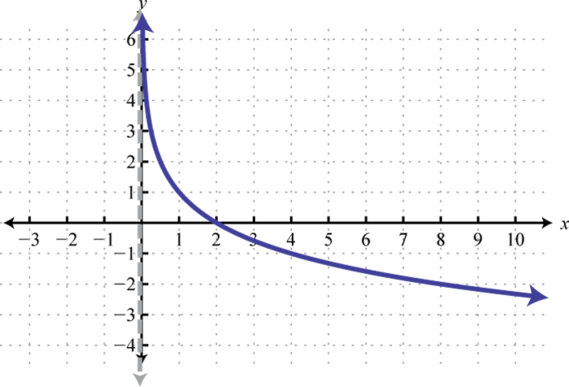
Figura\(\PageIndex{22}\) 9. Dominio:\((−∞, 0)\); Rango:\((−∞, ∞)\)
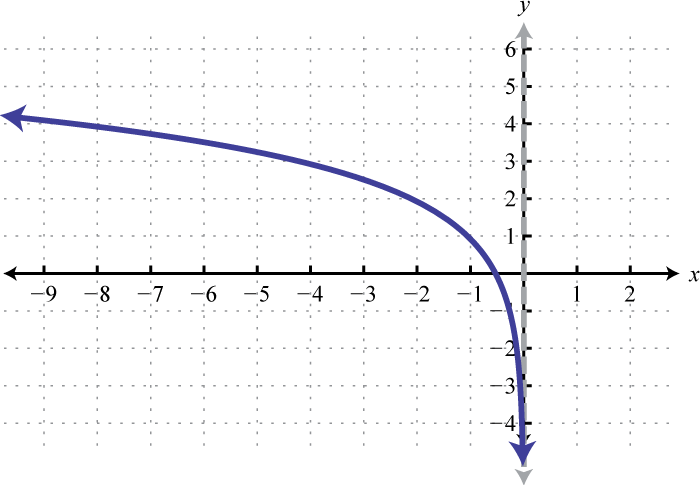
Figura\(\PageIndex{23}\) 11. Dominio:\((0, ∞)\); Rango:\((−∞, ∞)\)
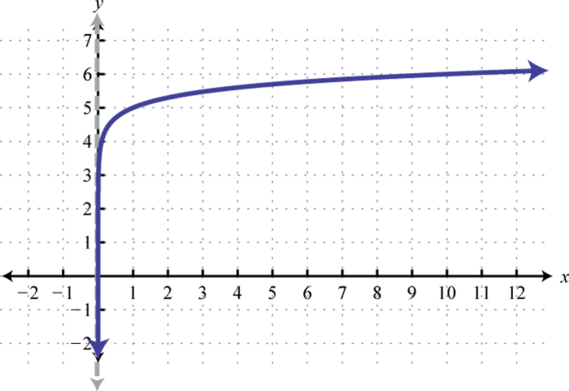
Figura\(\PageIndex{24}\) 13. Dominio:\((-4, ∞)\); Rango:\((−∞, ∞)\)
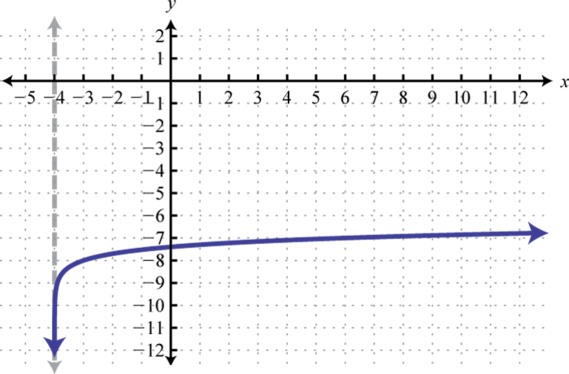
Figura\(\PageIndex{25}\) 15. Dominio:\((-2, ∞)\); Rango:\((−∞, ∞)\)
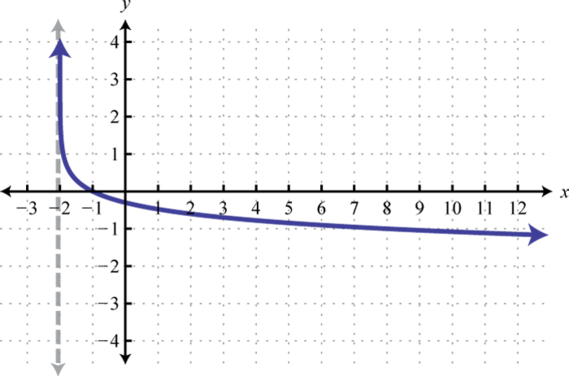
Figura\(\PageIndex{26}\) 17. Dominio:\((3, ∞)\); Rango:\((−∞, ∞)\)
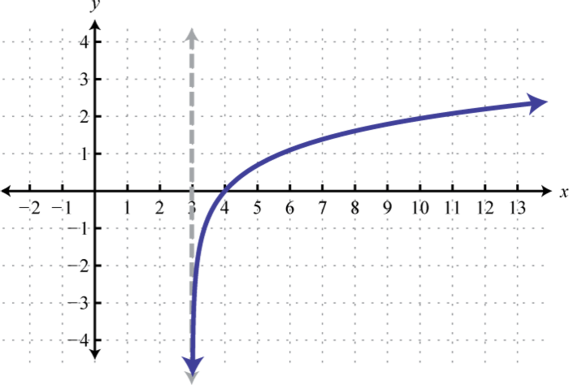
Figura\(\PageIndex{27}\) 19. Dominio:\((2, ∞)\); Rango:\((−∞, ∞)\)
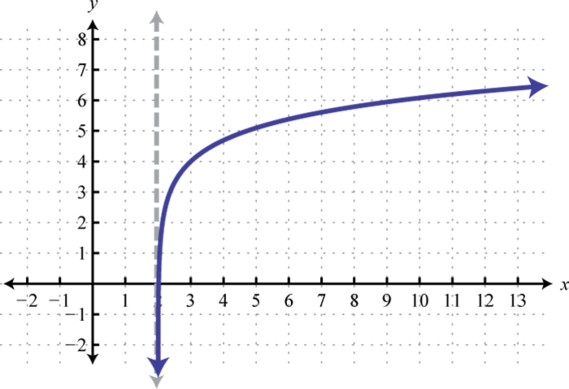
Figura\(\PageIndex{28}\) 21. Dominio:\((0, ∞)\); Rango:\((−∞, ∞)\)
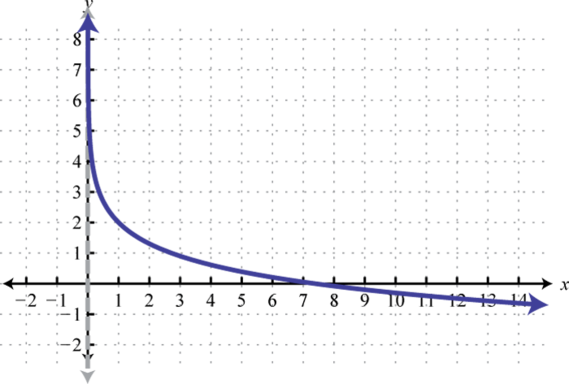
Figura\(\PageIndex{29}\) 23. Dominio:\((0, ∞)\); Rango:\((−∞, ∞)\)
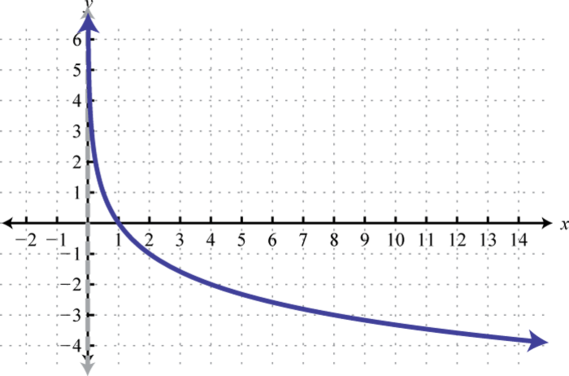
Figura\(\PageIndex{30}\) 25. Dominio:\((2, ∞)\); Rango:\((−∞, ∞)\)
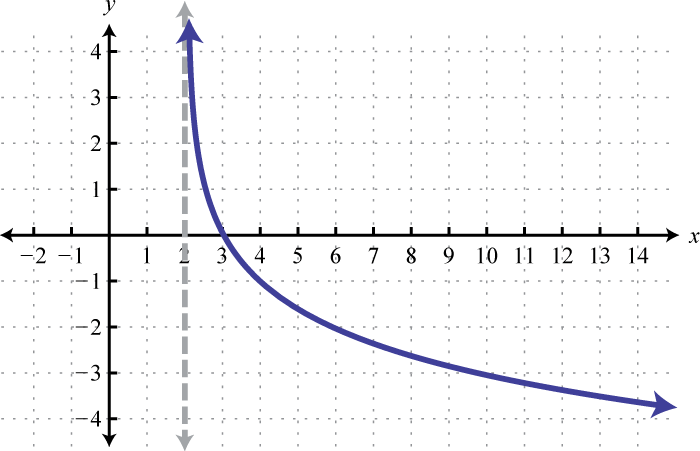
Figura\(\PageIndex{31}\) 27. Dominio:\((0, ∞)\); Rango:\((−∞, ∞)\)
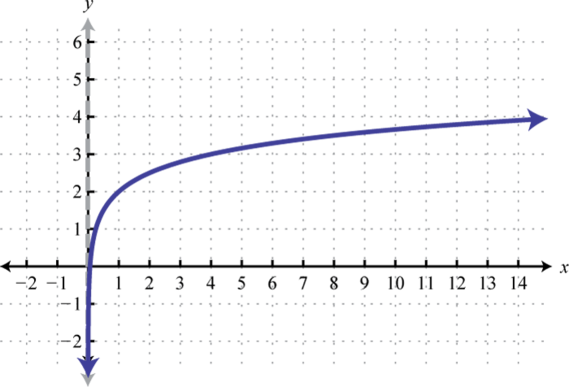
Figura\(\PageIndex{32}\) 29. Dominio:\((2, ∞)\); Rango:\((−∞, ∞)\)
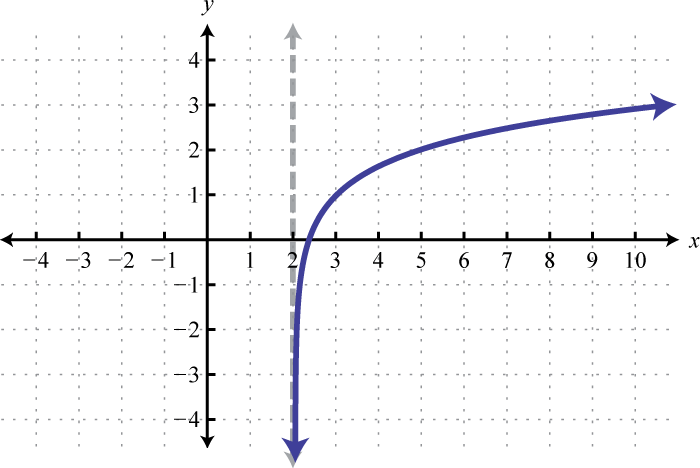
Figura\(\PageIndex{33}\)
Ejercicio\(\PageIndex{13}\)
- Investigar y discutir los orígenes e historia del logaritmo. ¿Cómo trabajaban los alumnos con ellos antes de la disponibilidad común de calculadoras?
- Investigar y discutir la historia y el uso de la escala Richter. ¿Qué representa cada unidad en la escala de Richter?
- Investigar y discutir la vida y contribuciones de John Napier.
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar


