7.5: Resolver ecuaciones exponenciales y logarítmicas

Última actualización
Guardar como PDF

Page ID: 109859

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Resolver ecuaciones exponenciales.
Utilice el cambio de fórmula base para aproximar logaritmos.
Resolver ecuaciones logarítmicas.

Resolver ecuaciones exponenciales

Una ecuación exponencial ¹⁵ es una ecuación que incluye una variable como uno de sus exponentes. En esta sección describimos dos métodos para resolver ecuaciones exponenciales. Primero, recordemos que las funciones exponenciales definidas por\(f (x) = b^{x}\) donde\(b > 0\) y\(b ≠ 1\), son uno-a-uno; cada valor en el rango corresponde exactamente a un elemento en el dominio. Por lo tanto,\(f (x) = f (y)\) implica\(x = y\). Lo contrario es cierto porque\(f\) es una función. Esto lleva a la muy importante propiedad uno-a-uno de las funciones exponenciales ¹⁶:

\(b^{\mathrm{x}}=b^{\mathrm{y}} \quad\)si y solo si\(\quad x=y\)

Utilice esta propiedad para resolver ecuaciones exponenciales especiales donde cada lado se puede escribir en términos de la misma base.

Ejemplo\(\PageIndex{1}\):

Resolver\(3^{2 x-1}=27\).

Solución

Comience por escribir\(27\) como un poder de\(3\).

\(3^{2 x-1}=27\)
\(3^{2 x-1}=3^{3}\)

A continuación, aplique la propiedad uno-a-uno de las funciones exponenciales. Es decir, establecer los exponentes iguales entre sí y luego simplificar.

\(2 x-1=3\)
\(2 x=4\)
\(x=2\)

Respuesta:

\(2\)

Ejemplo\(\PageIndex{2}\):

Resolver:\(16^{1-3 x}=2\).

Solución

Comience por escribir\(16\) como un poder de\(2\) y luego aplique la regla de poder para los exponentes.

\(\begin{aligned} 16^{1-3 x} &=2 \\\left(2^{4}\right)^{1-3 x} &=2 \\ 2^{4(1-3 x)} &=2^{1} \end{aligned}\)

Ahora que las bases son las mismas podemos establecer los exponentes iguales entre sí y simplificar.

\(\begin{aligned} 4(1-3 x) &=1 \\ 4-12 x &=1 \\-12 x &=-3 \\ x &=\frac{-3}{-12}=\frac{1}{4} \end{aligned}\)

Respuesta:

\(\frac{1}{4}\)

Ejercicio\(\PageIndex{1}\)

Resolver:\(25^{2 x+3}=125\).

Responder

\(-\frac{3}{4}\)

www.youtube.com/v/yu_tjg6unnc

En muchos casos no podremos equiparar las bases. Por esta razón desarrollamos un segundo método para resolver ecuaciones exponenciales. Considere las siguientes ecuaciones:

\(\begin{array}{l}{3^{2}=9} \\ {3^{\color{Cerulean}{?}}\color{black}{=}12} \\ {3^{3}=27}\end{array}\)

Podemos ver que la solución a\(3^{x} = 12\) debe estar en algún lugar entre\(2\) y\(3\). Sigue una interpretación gráfica.

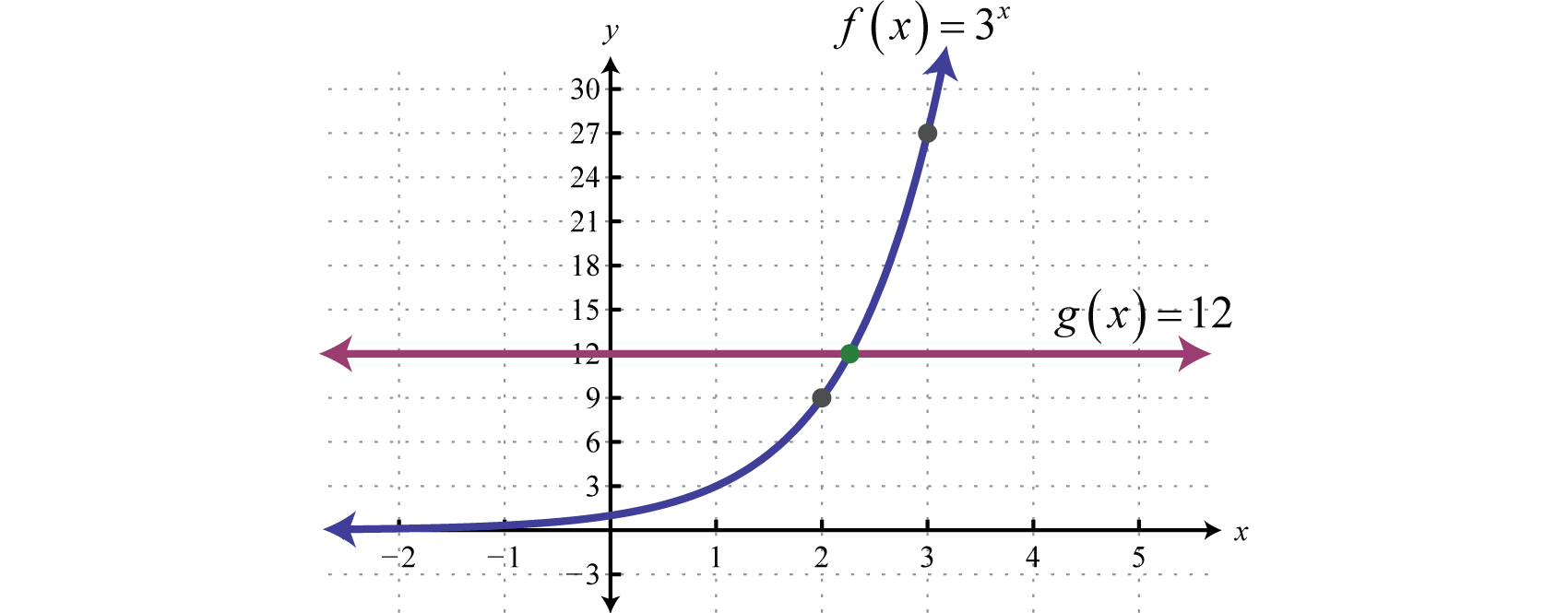
Para resolver esto hacemos uso del hecho de que los logaritmos son funciones uno-a-uno. Dada\(x, y > 0\) la propiedad uno-a-uno de logaritmos ¹⁷ sigue:

\(\log _{b} x=\log _{b} y \quad\)si y solo si\(\quad x=y\)

Esta propiedad, así como las propiedades del logaritmo, nos permite resolver ecuaciones exponenciales. Por ejemplo, para resolver\(3^{x} = 12\) aplicar el logaritmo común a ambos lados y luego usar las propiedades del logaritmo para aislar la variable.

\(\begin{aligned} 3^{x} &=12 \\ \log 3^{x} &=\log 12\quad\color{Cerulean}{One-to-one \:property\:of\:logarithms} \\ x \log 3 &=\log 12\quad\color{Cerulean}{Power\:rule\:for\:logarithms} \\ x &=\frac{\log 12}{\log 3} \end{aligned}\)

Aproximación a cuatro decimales en una calculadora.

\(x=\log (12) / \log (3) \approx 2.2619\)

Una respuesta entre\(2\) y\(3\) es lo que esperábamos. Ciertamente podemos verificar elevando\(3\) a esta facultad para verificar que obtenemos una buena aproximación de\(12\).

\(3\wedge 2.2618 \approx 12\:\:\color{Cerulean}{✓}\)

Tenga en cuenta que no estamos multiplicando ambos lados por “registro”; estamos aplicando la propiedad uno a uno de las funciones logarítmicas, que a menudo se expresa como “tomar el registro de ambos lados”. Los pasos generales para resolver ecuaciones exponenciales se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\):

Resolver:\(5^{2 x-1}+2=9\).

Solución

Paso 1: Aislar la expresión exponencial.

\(\begin{aligned} 5^{2 x-1}+2 &=9 \\ 5^{2 x-1} &=7 \end{aligned}\)

Paso 2: Toma el logaritmo de ambos lados. En este caso, tomaremos el logaritmo común de ambos lados para que podamos aproximar nuestro resultado en una calculadora.

\(\log 5^{2 x-1}=\log 7\)

Paso 3: Aplicar la regla de poder para logaritmos y luego resolver.

\(\begin{aligned} \log 5^{2 x-1} &=\log 7 \\(2 x-1) \log 5 &=\log 7\quad\quad\quad\quad\color{Cerulean}{Distribute.} \\ 2 x \log 5-\log 5 &=\log 7 \\ 2 x \log 5 &=\log 5+\log 7 \\ x &=\frac{\log 5+\log 7}{2 \log 5} \end{aligned}\)

Se trata de un número irracional que se puede aproximar usando una calculadora. Tenga cuidado de agrupar el numerador y el producto en el denominador al ingresar esto en su calculadora. Para ello, haga uso de los botones de paréntesis\((\) y\()\):

\(x=(\log 5+\log (7)) /(2 * \log (5)) \approx 1.1045\)

Respuesta:

\(\frac{\log 5+\log 7}{2 \log 5} \approx 1.1045\)

Ejemplo\(\PageIndex{4}\):

Resolver:\(e^{5 x+3}=1\).

Solución

La función exponencial ya está aislada y la base es\(e\). Por lo tanto, elegimos aplicar el logaritmo natural a ambos lados.

\(\begin{aligned} e^{5 x+3} &=1 \\ \ln e^{5 x+3} &=\ln 1 \end{aligned}\)

Aplicar la regla de potencia para logaritmos y luego simplificar.

\(\begin{aligned} \ln e^{5 x+3} &=\ln 1 \\(5 x+3) \ln e &=\ln 1 \quad\color{Cerulean}{Recall\:\ln e=1\:and\: \ln 1=0.} \\(5 x+3) \cdot 1 &=0 \\ 5 x+3 &=0 \\ x &=-\frac{3}{5} \end{aligned} \)

Respuesta:

\(-\frac{3}{5}\)

En la mayoría de las calculadoras solo hay dos botones de logaritmo, el logaritmo común\(LOG\) y el logaritmo natural\(LN\). Si queremos aproximarnos\(\log _{3} 10\) tenemos que cambiar de alguna manera esta base a\(10\) o\(e\). La idea comienza reescribiendo la función logarítmica\(y=\log _{a} x\), en forma exponencial.

\(\log _{a} x=y\color{Cerulean}{\Longrightarrow}\color{black}{x}=a^{y}\)

Aquí\(x > 0\) y así podemos aplicar la propiedad uno-a-uno de logaritmos. Aplicar la base logaritmo\(b\) a ambos lados de la función en forma exponencial.

\(\begin{aligned} x &=a^{y} \\ \log _{b} x &=\log _{b} a^{y} \end{aligned}\)

Y luego resolver para\(y\).

\(\log _{b} x=y \log _{b} a\)
\(\frac{\log _{b} x}{\log _{b} a}=y\)

Reemplazar\(y\) en la función original y tenemos el cambio muy importante de la fórmula base ¹⁸:

\(\log _{a} x=\frac{\log _{b} x}{\log _{b} a}\)

Podemos usar esto para aproximarnos de la\(\log _{3} 10\) siguiente manera.

\(\log _{3} 10=\frac{\log 10}{\log 3} \approx 2.0959\)o\(\log _{3} 10=\frac{\ln 10}{\ln 3} \approx 2.0959\)

Observe que el resultado es independiente de la elección de base. En palabras, podemos aproximar el logaritmo de cualquier base dada en una calculadora dividiendo el logaritmo del argumento por el logaritmo de esa base dada.

Ejemplo\(\PageIndex{5}\):

Aproximar\(\log _{7} 120\) la centésima más cercana.

Solución

Aplica el cambio de fórmula base y usa una calculadora.

\(\log _{7} 120=\frac{\log 120}{\log 7}\)

En una calculadora,

\(\log (120) / \log (7) \approx 2.46\)

Respuesta:

\(2.46\)

Ejercicio\(\PageIndex{2}\)

Resolver:\(2^{3 x+1}-4=1\). Dar la respuesta exacta y aproximada redondeada a cuatro decimales.

Responder

\(\frac{\log 5-\log 2}{3 \log 2} \approx 0.4406\)

www.youtube.com/v/kqf1-cequg8

Resolución de ecuaciones logarítmicas

Una ecuación logarítmica ¹⁹ es una ecuación que involucra un logaritmo con un argumento variable. Algunas ecuaciones logarítmicas se pueden resolver usando la propiedad uno-a-uno de logaritmos. Esto es cierto cuando se puede obtener un solo logaritmo con la misma base en ambos lados del signo igual.

Ejemplo\(\PageIndex{6}\):

Resolver:\(\log _{2}(2 x-5)-\log _{2}(x-2)=0\).

Solución

Podemos obtener dos logaritmos iguales base\(2\) sumando\(\log _{2}(x-2)\) a ambos lados de la ecuación.

\(\begin{aligned} \log _{2}(2 x-5)-\log _{2}(x-2)&=0 \\ \log _{2}(2 x-5) &=\log _{2}(x-2) \end{aligned}\)

Aquí las bases son las mismas y así podemos aplicar la propiedad uno-a-uno y establecer los argumentos iguales entre sí.

\(\begin{aligned} \log _{2}(2 x-5) &=\log _{2}(x-2) \\ 2 x-5 &=x-2 \\ x &=3 \end{aligned}\)

Comprobación\(x=3\) de la ecuación original:

\(\begin{aligned} \log _{2}(2(\color{OliveGreen}{3}\color{black}{)}-5) &=\log _{2}((\color{OliveGreen}{3}\color{black}{)}-2) \\ \log _{2} 1 &=\log _{2} 1 \\ 0 &=0\:\:\color{Cerulean}{✓} \end{aligned}\)

Respuesta:

\(3\)

Al resolver ecuaciones logarítmicas la comprobación es muy importante porque se pueden obtener soluciones extrañas. Las propiedades del logaritmo solo aplican para valores en el dominio del logaritmo dado. Y cuando se trabaja con argumentos variables, como\(\log (x-2)\), el valor de no\(x\) se conoce hasta el final de este proceso. La expresión logarítmica solo\(\log (x-2)\) se define para los valores\(x > 2\).

Ejemplo\(\PageIndex{7}\):

Resolver:\(\log (3 x-4)=\log (x-2)\).

Solución

Aplicar la propiedad uno a uno de logaritmos (establecer los argumentos iguales entre sí) y luego resolver para\(x\).

\(\begin{aligned} \log (3 x-4) &=\log (x-2) \\ 3 x-4 &=x-2 \\ 2 x &=2 \\ x &=1 \end{aligned}\)

Al realizar la comprobación nos encontramos con un logaritmo de un número negativo:

\(\begin{aligned} \log (x-2) &=\log (\color{Cerulean}{1}\color{black}{-}2) \\ &=\log (-1) \quad \color{Cerulean} { Undefined } \end{aligned}\)

Prueba esto en una calculadora, ¿qué dice? Aquí no\(x = 1\) está en el dominio de\(\log (x-2)\). Por lo tanto, nuestra única solución posible es ajena y concluimos que no hay soluciones a esta ecuación.

Responder

Sin solución,\(\emptyset\).

Precaución: Resolver ecuaciones logarítmicas a veces conduce a soluciones extrañas; debemos verificar nuestras respuestas.

Ejercicio\(\PageIndex{3}\)

Resolver:\( \ln \left(x^{2}-15\right)-\ln (2 x)=0\).

Responder

\(5\)

www.youtube.com/V/-KBKK-Q2PNs

En muchos casos no podremos obtener dos logaritmos iguales. Para resolver tales ecuaciones hacemos uso de la definición del logaritmo. Si\(b > 0\), donde\(b ≠ 1\), entonces\(\log _{b} x=y\) implica eso\(b^{y} = x\). Considere las siguientes ecuaciones logarítmicas comunes (base\(10\)),

\(\begin{array}{l}{\log x=0\Longrightarrow =1 \quad\:\;\color{Cerulean}{Because\: 10^{10}=1.}} \\ {\log x=0.5\Longrightarrow=\color{Cerulean}{?}} \\ {\log x=1\Longrightarrow=10\quad\color{Cerulean}{Because\:10^{1}=10.}}\end{array}\)

Podemos ver que la solución a\(\log x=0.5\) va a estar en algún lugar entre\(1\) y\(10\). Sigue una interpretación gráfica.

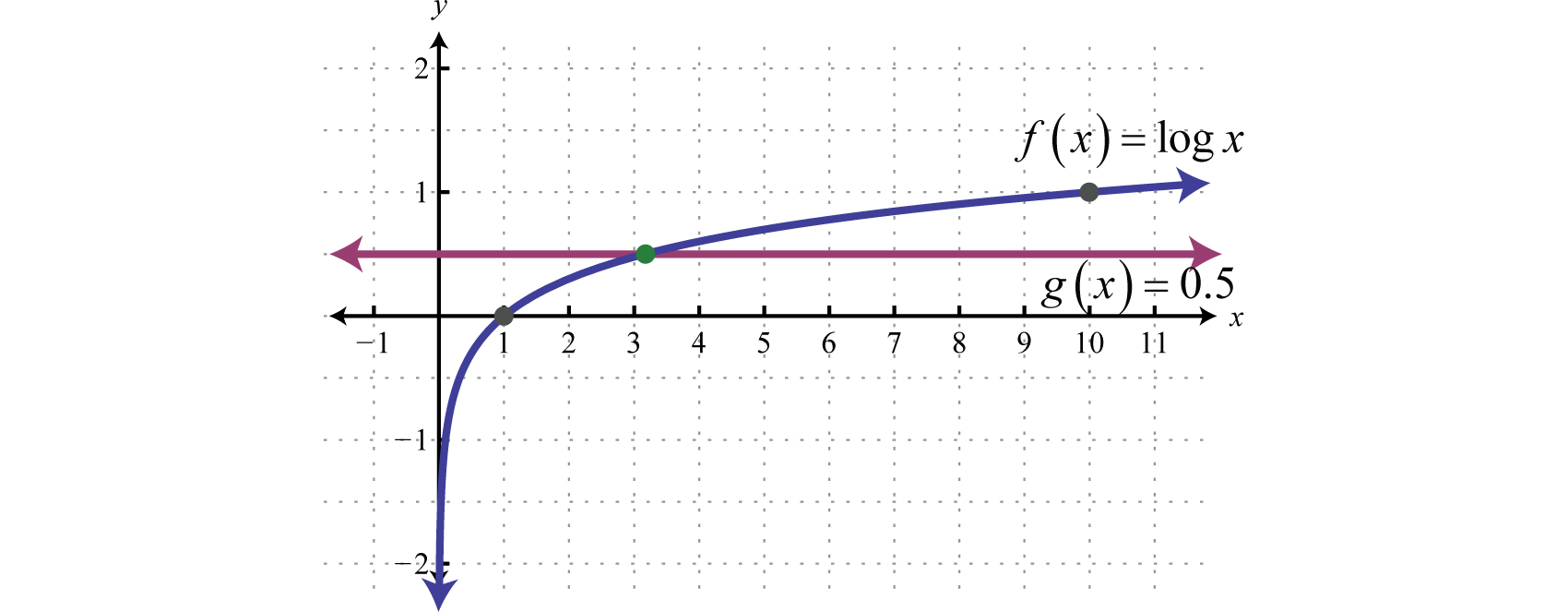
Para encontrar\(x\) podemos aplicar la definición de la siguiente manera.

\(\log _{10} x=0.5\Longrightarrow10^{0.5}=x\)

Esto se puede aproximar usando una calculadora,

\(x=10^{0.5}=10^{\wedge} 0.5 \approx 3.1623\)

Una respuesta entre\(1\) y\(10\) es lo que esperábamos. Consulta esto en una calculadora.

\(\log 3.1623 \approx 5\:\:\color{Cerulean}{✓}\)

Ejemplo\(\PageIndex{8}\):

Resolver:\(\log _{3}(2 x-5)=2\).

Solución

Aplicar la definición del logaritmo.

\(\log _{3}(2 x-5)=2\color{Cerulean}{\Longrightarrow}\color{black}{2x}-5=3^{2}\)

Resuelve la ecuación resultante.

\(\begin{aligned}2 x-5&=9 \\ 2 x&=14 \\ x&=7 \end{aligned}\)

Cheque.

\(\begin{aligned} \log _{3}(2(\color{OliveGreen}{7}\color{black}{)}-5) &\stackrel{?}{=}2 \\ \log _{3}(9) &=2\:\:\color{Cerulean}{✓} \end{aligned}\)

Respuesta:

\(7\)

Para aplicar la definición, necesitaremos reescribir expresiones logarítmicas como un logaritmo único con coeficiente\(1\). Los pasos generales para resolver ecuaciones logarítmicas se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{9}\):

Resolver:\(\log _{2}(x-2)+\log _{2}(x-3)=1\).

Solución

Paso 1: Escribe todas las expresiones logarítmicas como un solo logaritmo con coeficiente\(1\). En este caso, aplicar la regla del producto para logaritmos.

\(\begin{aligned} \log _{2}(x-2)+\log _{2}(x-3) &=1 \\ \log _{2}[(x-2)(x-3)] &=1 \end{aligned}\)

Paso 2: Usa la definición y reescribe el logaritmo en forma exponencial,

\(\log _{2}[(x-2)(x-3)]=1\color{Cerulean}{\Longrightarrow}\color{black}{(}x-2)(x-3)=2^{1}\)

Paso 3: Resolver la ecuación resultante. Aquí podemos resolver factorizando.

\(\begin{array}{rl}{(x-2)(x-3)} & {=2} \\ {x^{2}-5 x+6} & {=2} \\ {x^{2}-5 x+4} & {=0} \\ {(x-4)(x-1)} & {=0} \\ {x-4} & {=0} \quad\text{or}\quad& {x-1=0} \\ {x} & {=4} & {\quad\:\:\: x=1}\end{array}\)

Paso 4: Comprobar. Este paso es requerido.

Mesa\(\PageIndex{1}\)
Cheque\(x=4\)	Cheque\(x=1\)
\(\begin{aligned} \log _{2}(x-2)+\log _{2}(x-3) &=1 \\ \log _{2}(\color{Cerulean}{4}\color{black}{-}2)+\log _{2}(\color{Cerulean}{4}\color{black}{-}3) &=1 \\ \log _{2}(2)+\log _{2}(1) &=1 \\ 1+0 &=1\:\:\color{Cerulean}{✓} \end{aligned}\)	\(\begin{aligned}\log _{2}(x-2)+\log _{2}(x-3)&=1 \\ \log _{2}(\color{Cerulean}{1}\color{black}{-}2)+\log _{2}(\color{Cerulean}{1}\color{black}{-}3)&=1 \\ \log _{2}(-1)+\log _{2}(-2)&=1\\N/A&\neq1\:\:\color{red}{✗}\end{aligned}\)

En este ejemplo, no\(x=1\) está en el dominio de la expresión logarítmica dada y es ajena. La única solución es\(x=4\).

Respuesta:

\(4\)

Ejemplo\(\PageIndex{10}\):

Resolver:\(\log (x+15)-1=\log (x+6)\)

Solución

Comience por escribir todas las expresiones logarítmicas en un lado y constantes en el otro.

\(\begin{aligned} \log (x+15)-1 &=\log (x+6) \\ \log (x+15)-\log (x+6) &=1 \end{aligned}\)

Aplicar la regla del cociente para logaritmos como media para obtener un logaritmo único con coeficiente\(1\).

\(\log (x+15)-\log (x+6)=1\)
\(\log \left(\frac{x+15}{x+6}\right)=1\)

Este es un logaritmo común; por lo tanto, utilizar 10 como base al aplicar la definición.

\(\begin{aligned} \frac{x+15}{x+6} &=10^{1} \\ x+15 &=10(x+6) \\ x+15 &=10 x+60 \\-9 x &=45 \\ x &=-5 \end{aligned}\)

Cheque.

\(\begin{aligned} \log (x+15)-1 &=\log (x+6) \\ \log (-\color{OliveGreen}{5}\color{black}{+}15)-1 &=\log (-\color{OliveGreen}{5}\color{black}{+}6) \\ \log 10-1 &=\log 1 \\ 1-1 &=0 \\ 0 &=0\:\:\color{Cerulean}{✓} \end{aligned}\)

Respuesta:

\(-5\)

Ejercicio\(\PageIndex{4}\)

Resolver:\(\log _{2}(x)+\log _{2}(x-1)=1\).

Responder

\(2\)

www.youtube.com/v/lzwh1jkj-ey

Ejemplo\(\PageIndex{11}\):

Encuentra lo inverso:\(f(x)=\log _{2}(3 x-4)\).

Solución

Comience reemplazando la notación de la función\(f(x)\) con\(y\).

\(\begin{aligned} f(x) &=\log _{2}(3 x-4) \\ y &=\log _{2}(3 x-4) \end{aligned}\)

\(x\)Intercambiar\(y\) y luego resolver para\(y\).

\(\begin{aligned}x=\log _{2}(3 y-4)\color{Cerulean}{\Longrightarrow}\color{black}{3}y-4&=2^{x}\\3y&=2^{x}+4\\y&=\frac{2^{x}+4}{3} \end{aligned}\)

La función resultante es la inversa de\(f\). Presentar la respuesta usando notación de funciones.

Respuesta:

\(f^{-1}(x)=\frac{2^{x}+4}{3}\)

Claves para llevar

Si cada lado de una ecuación exponencial se puede expresar usando la misma base, entonces equiparar los exponentes y resolver.
Para resolver una ecuación exponencial general, primero aísle la expresión exponencial y luego aplique el logaritmo apropiado a ambos lados. Esto nos permite utilizar las propiedades de logaritmos para resolver para la variable.
El cambio de fórmula base nos permite utilizar una calculadora para calcular logaritmos. El logaritmo de un número es igual al logaritmo común del número dividido por el logaritmo común de la base dada.
Si un solo logaritmo con la misma base puede aislarse en cada lado de una ecuación, entonces equiparar los argumentos y resolver.
Para resolver una ecuación logarítmica general, primero aísle el logaritmo con coeficiente\(1\) y luego aplicar la definición. Resuelve la ecuación resultante.
Los pasos para resolver ecuaciones logarítmicas a veces producen soluciones extrañas. Por lo tanto, se requiere el cheque.

Ejercicio\(\PageIndex{5}\)

Resuelve usando la propiedad uno a uno de las funciones exponenciales.

\(3^{x}=81\)
\(2^{-x}=16\)
\(5^{x-1}=25\)
\(3^{x+4}=27\)
\(2^{5 x-2}=16\)
\(2^{3 x+7}=8\)
\(81^{2 x+1}=3\)
\(64^{3 x-2}=2\)
\(9^{2-3 x}-27=0\)
\(8^{1-5 x}-32=0\)
\(16^{x^{2}}-2=0\)
\(4^{x^{2}-1}-64=0\)
\(9^{x(x+1)}=81\)
\(4^{x(2 x+5)}=64\)
\(100^{x^{2}}-10^{7 x-3}=0\)
\(e^{3\left(3 x^{2}-1\right)}-e=0\)

Responder

1. \(4\)

3. \(3\)

5. \(\frac{6}{5}\)

7. \(-\frac{3}{8}\)

9. \(\frac{1}{6}\)

11. \(\pm \frac{1}{2}\)

13. \(-2,1\)

15. \(\frac{1}{2}, 3\)

Ejercicio\(\PageIndex{6}\)

Resolver. Dar la respuesta exacta y la respuesta aproximada redondeada a la milésima más cercana.

\(3^{x}=5\)
\(7^{x}=2\)
\(4^{x}=9\)
\(2^{x}=10\)
\(5^{x-3}=13\)
\(3^{x+5}=17\)
\(7^{2 x+5}=2\)
\(3^{5 x-9}=11\)
\(5^{4 x+3}+6=4\)
\(10^{7 x-1}-2=1\)
\(e^{2 x-3}-5=0\)
\(e^{5 x+1}-10=0\)
\(6^{3 x+1}-3=7\)
\(8-10^{9 x+2}=9\)
\(15-e^{3 x}=2\)
\(7+e^{4 x+1}=10\)
\(7-9 e^{-x}=4\)
\(3-6 e^{-x}=0\)
\(5^{x^{2}}=2\)
\(3^{2 x^{2}-x}=1\)
\(100 e^{27 x}=50\)
\(6 e^{12 x}=2\)
\(\frac{3}{1+e^{-x}}=1\)
\(\frac{2}{1+3 e^{-x}}=1\)

Responder

1. \(\frac{\log 5}{\log 3} \approx 1.465\)

3. \(\frac{\log 3}{\log 2} \approx 1.585\)

5. \(\frac{3 \log 5+\log 13}{\log 5} \approx 4.594\)

7. \(\frac{\log 2-5 \log 7}{2 \log 7} \approx-2.322\)

9. \(\varnothing\)

11. \(\frac{3+\ln 5}{2} \approx 2.305\)

13. \(\frac{1-\log 6}{3 \log 6} \approx 0.095\)

15. \(\frac{\ln 13}{3} \approx 0.855\)

17. \(\ln 3 \approx 1.099\)

19. \(\pm \sqrt{\frac{\log 2}{\log 5}} \approx \pm 0.656\)

21. \(-\frac{\ln 2}{27} \approx-0.026\)

23. \(-\ln 2 \approx-0.693\)

Ejercicio\(\PageIndex{7}\)

Encuentra las\(y\) intercepciones\(x\) - y -de la función dada.

\(f(x)=3^{x+1}-4\)
\(f(x)=2^{3 x-1}-1\)
\(f(x)=10^{x+1}+2\)
\(f(x)=10^{4 x}-5\)
\(f(x)=e^{x-2}+1\)
\(f(x)=e^{x+4}-4\)

Responder

1. \(x\)-interceptar:\(\left(\frac{2 \log 2-\log 3}{\log 3}, 0\right)\);\(y\) -interceptar:\((0, −1)\)

3. \(x\)-interceptar: Ninguno;\(y\) -interceptar:\((0, 12)\)

5. \(x\)-interceptar: Ninguno;\(y\) -interceptar:\(\left(0, \frac{1+e^{2}}{e^{2}}\right)\)

Ejercicio\(\PageIndex{8}\)

Utilice una\(u\) -sustitución para resolver lo siguiente.

\(3^{2 x}-3^{x}-6=0\)Pista: Let\(u=3^{x}\)
\(2^{2 x}+2^{x}-20=0\)
\(10^{2 x}+10^{x}-12=0\)
\(10^{2 x}-10^{x}-30=0\)
\(e^{2 x}-3 e^{x}+2=0\)
\(e^{2 x}-8 e^{x}+15=0\)

Responder

1. \(1\)

3. \(\log 3\)

5. \(0, \ln 2\)

Ejercicio\(\PageIndex{9}\)

Utilice el cambio de fórmula base para aproximar lo siguiente a la centésima más cercana.

\(\log _{2} 5\)
\(\log _{3} 7\)
\(\log _{5}\left(\frac{2}{3}\right)\)
\(\log _{7}\left(\frac{1}{5}\right)\)
\(\log _{1 / 2} 10\)
\(\log _{2 / 3} 30\)
\(\log _{2} \sqrt{5}\)
\(\log _{2} \sqrt[3]{6}\)
Si no se controla, una nueva cepa del virus de la gripe puede propagarse de una sola persona a otras muy rápidamente. El número de personas afectadas se puede modelar usando la fórmula\(P (t) = e^{0.22t}\), donde\(t\) representa el número de días que se permite que el virus se propague sin marcar. Estimar el número de días que tardará a\(1,000\) las personas en infectarse.
La población de un determinado pueblo pequeño está creciendo de acuerdo a la función\(P (t) = 12,500(1.02)^{t}\), donde\(t\) representa el tiempo en años desde el último censo. Utilizar la función para determinar el número de años que tardará la población en crecer a\(25,000\) personas.

Responder

1. \(2.32\)

3. \(−0.25\)

5. \(−3.32\)

7. \(1.16\)

9. \(31\)Días aproximadamente

Ejercicio\(\PageIndex{10}\)

Resuelve usando la propiedad uno-a-uno de logaritmos.

\(\log _{5}(2 x+4)=\log _{5}(3 x-6)\)
\(\log _{4}(7 x)=\log _{4}(5 x+14)\)
\(\log _{2}(x-2)-\log _{2}(6 x-5)=0\)
\(\ln (2 x-1)=\ln (3 x)\)
\(\log (x+5)-\log (2 x+7)=0\)
\(\ln \left(x^{2}+4 x\right)=2 \ln (x+1)\)
\(\log _{3} 2+2 \log _{3} x=\log _{3}(7 x-3)\)
\(2 \log x-\log 36=0\)
\(\ln (x+3)+\ln (x+1)=\ln 8\)
\(\log _{5}(x-2)+\log _{5}(x-5)=\log _{5} 10\)

Responder

1. \(10\)

3. \(\frac{3}{5}\)

5. \(−2\)

7. \(\frac{1}{2} , 3\)

9. \(1\)

Ejercicio\(\PageIndex{11}\)

Resolver.

\(\log _{2}(3 x-7)=5\)
\(\log _{3}(2 x+1)=2\)
\(\log (2 x+20)=1\)
\(\log _{4}(3 x+5)=\frac{1}{2}\)
\(\log _{3} x^{2}=2\)
\(\log \left(x^{2}+3 x+10\right)=1\)
\(\ln \left(x^{2}-1\right)=0\)
\(\log _{5}\left(x^{2}+20\right)-2=0\)
\(\log _{2}(x-5)+\log _{2}(x-9)=5\)
\(\log _{2}(x+5)+\log _{2}(x+1)=5\)
\(\log _{4} x+\log _{4}(x-6)=2\)
\(\log _{6} x+\log _{6}(2 x-1)=2\)
\(\log _{3}(2 x+5)-\log _{3}(x-1)=2\)
\(\log _{2}(x+1)-\log _{2}(x-2)=4\)
\(\ln x-\ln (x-1)=1\)
\(\ln (2 x+1)-\ln x=2\)
\(2 \log _{3} x=2+\log _{3}(2 x-9)\)
\(2 \log _{2} x=3+\log _{2}(x-2)\)
\(\log _{2}(x-2)=2-\log _{2} x\)
\(\log _{2}(x+3)+\log _{2}(x+1)-1=0\)
\(\log x-\log (x+1)=1\)
\(\log _{2}(x+2)+\log _{2}(1-x)=1+\log _{2}(x+1)\)

Responder

1. \(13\)

3. \(−5\)

5. \(±3\)

7. \(\pm \sqrt{2}\)

9. \(13\)

11. \(8\)

13. \(2\)

15. \(\frac{e}{e-1}\)

17. \(9\)

19. 1\(\pm \sqrt{5}\)

21. \(Ø\)

Ejercicio\(\PageIndex{12}\)

Encuentra las\(y\) intercepciones\(x\) - y -de la función dada.

\(f(x)=\log (x+3)-1\)
\(f(x)=\log (x-2)+1\)
\(f(x)=\log _{2}(3 x)-4\)
\(f(x)=\log _{3}(x+4)-3\)
\(f(x)=\ln (2 x+5)-6\)
\(f(x)=\ln (x+1)+2\)

Responder

1. \(x\)-interceptar:\((7, 0)\);\(y\) -interceptar:\((0, \log 3-1)\)

3. \(x\)-interceptar:\((\frac{16}{3}, 0)\);\(y\) -interceptar: Ninguno

5. \(x\)-interceptar:\(\left(\frac{e^{6}-5}{2}, 0\right)\);\(y\) -interceptar:\((0, \ln 5-6)\)

Ejercicio\(\PageIndex{13}\)

Encuentra la inversa de las siguientes funciones.

\(f(x)=\log _{2}(x+5)\)
\(f(x)=4+\log _{3} x\)
\(f(x)=\log (x+2)-3\)
\(f(x)=\ln (x-4)+1\)
\(f(x)=\ln (9 x-2)+5\)
\(f(x)=\log _{6}(2 x+7)-1\)
\(g(x)=e^{3 x}\)
\(g(x)=10^{-2 x}\)
\(g(x)=2^{x+3}\)
\(g(x)=3^{2 x}+5\)
\(g(x)=10^{x+4}-3\)
\(g(x)=e^{2 x-1}+1\)

Responder

1. \(f^{-1}(x)=2^{x}-5\)

3. \(f^{-1}(x)=10^{x+3}-2\)

5. \(f^{-1}(x)=\frac{e^{x-5}+2}{9}\)

7. \(g^{-1}(x)=\frac{\ln x}{3}\)

9. \(g^{-1}(x)=\log _{2} x-3\)

11. \(g^{-1}(x)=\log (x+3)-4\)

Ejercicio\(\PageIndex{14}\)

Resolver.

\(\log (9 x+5)=1+\log (x-5)\)
\(2+\log _{2}\left(x^{2}+1\right)=\log _{2} 13\)
\(e^{5 x-2}-e^{3 x}=0\)
\(3^{x^{2}}-11=70\)
\(2^{3 x}-5=0\)
\(\log _{7}(x+1)+\log _{7}(x-1)=1\)
\(\ln (4 x-1)-1=\ln x\)
\(\log (20 x+1)=\log x+2\)
\(\frac{3}{1+e^{2 x}}=2\)
\(2 e^{-3 x}=4\)
\(2 e^{3 x}=e^{4 x+1}\)
\(2 \log x+\log x-1=0\)
\(3 \log x=\log (x-2)+2 \log x\)
\(2 \ln 3+\ln x^{2}=\ln \left(x^{2}+1\right)\)
En química, el pH es una medida de acidez y viene dado por la fórmula\(\mathrm{pH}=-\log \left(H^{+}\right)\), donde\(H^{+}\) está la concentración de iones hidrógeno (medida en moles de hidrógeno por litro de solución). Determinar la concentración de iones hidrógeno si el pH de una solución es\(4\).
El volumen de sonido,\(L\) en decibelios (dB), viene dado por la fórmula\(L=10 \log \left(I / 10^{-12}\right)\) donde\(I\) representa la intensidad del sonido en vatios por metro cuadrado. Determinar la intensidad de una alarma que emite\(120\) dB de sonido.

Responder

1. \(55\)

3. \(1\)

5. \(\frac{\log _{2} 5}{3}\)

7. \(\frac{1}{4-e}\)

9. \(\frac{\ln (1 / 2)}{2}\)

11. \(\ln 2-1\)

13. \(\emptyset\)

15. \(10^{-4}\)moles por litro

Ejercicio\(\PageIndex{15}\)

Investigar y discutir la historia y el uso de la regla de cálculo.
Investigar y discutir aplicaciones del mundo real que involucran logaritmos.

Responder: 1. La respuesta puede variar

Notas al pie

¹⁵ Ecuación que incluye una variable como exponente.

¹⁶ Dado\(b > 0\) y\(b ≠ 1\) tenemos\(b^{x} = b^{y}\) si y solo si\(x = y\).

¹⁷ Dado\(b > 0\) y\(b ≠ 1\) donde\(x, y > 0\) tenemos\(log_{b}x = log_{b}y\) si y solo si\(x = y\).

¹⁸\(\log _{a} x=\frac{\log _{b} x}{\log _{b} a}\); podemos escribir cualquier\(a\) logaritmo base en términos de\(b\) logaritmos base usando esta fórmula.

¹⁹ Ecuación que implica un logaritmo con un argumento variable.