9.1: Introducción a las Secuencias y Series

Última actualización
Guardar como PDF

Page ID: 109731

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Habilidades para Desarrollar

Encontrar cualquier elemento de una secuencia dada una fórmula para su término general.
Utilice la notación sigma y expanda las series correspondientes.
Distinguir entre una secuencia y una serie.
Calcular la$n$ ésima suma parcial de secuencia.

Secuencias

Una secuencia ¹ es una función cuyo dominio es un conjunto de números naturales consecutivos que comienzan con$1$. Por ejemplo, la siguiente ecuación con dominio$\{1,2,3, \dots\}$ define una secuencia infinita ²:

$a(n)=5 n-3$o$a_{n}=5 n-3$

Los elementos en el rango de esta función se denominan términos de la secuencia. Es común definir el término$n$ th, o el término general de una secuencia ³, usando la notación subíndice$a_{n}$, que dice “$a$sub”$n$. Los términos se pueden encontrar usando la sustitución de la siguiente manera:

$\begin{aligned}\color{Cerulean} { General\: term: } \quad &\color{black}{a_{n}=5 n-3} \\ \color{Cerulean} { First\: term (n=1) :}\quad & \color{black}{a_{1}=}5(\color{Cerulean}{1}\color{black}{)}-3=2 \\ \color{Cerulean}{Second\:term(n=2):} \quad& \color{black}{a_{2}=5}(\color{Cerulean}{2}\color{black}{)}-3=7 \\ \color{Cerulean}{Third\:term(n=3):} \quad& \color{black}{a_{3}=5}(\color{Cerulean}{3}\color{black}{)}-3=12 \\\color{Cerulean}{Fourth\:term(n=4):} \quad& \color{black}{a_{4}=5}(\color{Cerulean}{4}\color{black}{)}-3=17 \\ \color{Cerulean}{Fifth\:term(n=5):} \quad& \color{black}{a_{5}=5}(\color{Cerulean}{5}\color{black}{)}-3=22 \\ \vdots\end{aligned}$

Esto produce una lista ordenada,

$2,7,12,17,22, \ldots$

Los puntos suspensivos$(…)$ indican que esta secuencia continúa para siempre. A diferencia de un conjunto, el orden importa. Si el dominio de una secuencia consiste en números naturales que terminan, tal como$\{1,2,3, \ldots, k\}$, entonces se llama secuencia finita ⁴.

Ejemplo$\PageIndex{1}$:

Dado el término general de una secuencia, encontrar los primeros$5$ términos así como el$100^{th}$ término:$a_{n}=\frac{n(n-1)}{2}$.

Solución:

Para encontrar los primeros$5$ términos, sustituir$1, 2, 3, 4$, y$5$ para$n$ y luego simplificar.

$\begin{array}{l}{a_{1}=\frac{\color{Cerulean}{1}\color{black}{(}\color{Cerulean}{1}\color{black}{-}1)}{2}=\frac{1(0)}{2}=\frac{0}{2}=0} \\ {a_{2}=\frac{\color{Cerulean}{2}\color{black}{(}\color{Cerulean}{2}\color{black}{-}1)}{2}=\frac{2(1)}{2}=\frac{2}{2}=1} \\ {a_{3}=\frac{\color{Cerulean}{3}\color{black}{(}\color{Cerulean}{3}\color{black}{-}1)}{2}=\frac{3(2)}{2}=\frac{6}{2}=3} \\ {a_{4}=\frac{\color{Cerulean}{4}\color{black}{(}\color{Cerulean}{4}\color{black}{-}1)}{2}=\frac{4(3)}{2}=\frac{12}{2}=6} \\ {a_{5}=\frac{\color{Cerulean}{5}\color{black}{(}\color{Cerulean}{5}\color{black}{-}1)}{2}=\frac{5(4)}{2}=\frac{20}{2}=10}\end{array}$

Utilízala$n = 100$ para determinar el$100^{th}$ término en la secuencia.

$a_{100}=\frac{100(100-1)}{2}=\frac{100(99)}{2}=\frac{9,900}{2}=4,950$

Respuesta:

Primeros cinco términos:$0, 1, 3, 6, 10$;$a_{100} = 4,950$

En ocasiones el término general de una secuencia se alternará en signo y tendrá una variable distinta a$n$.

Ejemplo$\PageIndex{2}$:

Encuentra los primeros$5$ términos de la secuencia:$a_{n}=(-1)^{n} x^{n+1}$.

Solución:

Aquí nos encargamos de reemplazar$n$ con los primeros números$5$ naturales y no$x$.

$\begin{array}{l}{a_{1}=(-1)\color{Cerulean}{^{1}}\color{black}{ x}^{\color{Cerulean}{1}\color{black}{+}1}=-x^{2}} \\ {a_{2}=(-1)^{\color{Cerulean}{2}}\color{black}{ x}^{\color{Cerulean}{2}\color{black}{+}1}=x^{3}} \\ {a_{3}=(-1)^{\color{Cerulean}{3}} \color{black}{x}^{\color{Cerulean}{3}\color{black}{+}1}=-x^{4}} \\ {a_{4}=(-1)^{\color{Cerulean}{4}}\color{black}{ x}^{\color{Cerulean}{4}\color{black}{+}1}=x^{5}} \\ {a_{5}=(-1)^{\color{Cerulean}{5}}\color{black}{ x}^{\color{Cerulean}{5}\color{black}{+}1}=-x^{6}}\end{array}$

Respuesta:

$-x^{2}, x^{3},-x^{4}, x^{5},-x^{6}$

Ejercicio$\PageIndex{1}$

Encuentra los primeros$5$ términos de la secuencia:$a_{n}=(-1)^{n+1} 2^{n}$.

Contestar

$2, −4, 8, −16, 32.$

http://www.youtube.com/v/uuQ3jYL-g_I

Un ejemplo interesante es la secuencia de Fibonacci. Los dos primeros números de la secuencia de Fibonacci son$1$, y cada término sucesivo es la suma de los dos anteriores. Por lo tanto, el término general se expresa en términos de los dos anteriores de la siguiente manera:

$F_{n}=F_{n-2}+F_{n-1}$

Aquí$F_{1} = 1, F_{2} = 1$, y$n > 2$. Una fórmula que describe una secuencia en términos de sus términos anteriores se denomina relación de recurrencia ⁵.

Ejemplo$\PageIndex{3}$:

Encuentra los primeros números de$7$ Fibonacci.

Solución:

Dado eso$F_{1} = 1$ y$F_{2} = 1$, usa la relación de recurrencia$F_{n}=F_{n-2}+F_{n-1}$ donde$n$ es un número entero que comienza con$n = 3$ para encontrar los siguientes$5$ términos:

$\begin{array}{l}{F_{3}=F_{\color{Cerulean}{3}\color{black}{-}2}+F_{\color{Cerulean}{3}\color{black}{-}1}=F_{1}+F_{2}=1+1=2} \\ {F_{4}=F_{\color{Cerulean}{4}\color{black}{-}2}+F_{\color{Cerulean}{4}\color{black}{-}1}=F_{2}+F_{3}=1+2=3} \\ {F_{5}=F_{\color{Cerulean}{5}\color{black}{-}2}+F_{\color{Cerulean}{5}\color{black}{-}1}=F_{3}+F_{4}=2+3=5} \\ {F_{6}=F_{\color{Cerulean}{6}\color{black}{-}2}+F_{\color{Cerulean}{6}\color{black}{-}1}=F_{4}+F_{5}=3+5=8} \\ {F_{7}=F_{\color{Cerulean}{7}\color{black}{-}2}+F_{\color{Cerulean}{7}\color{black}{-}1}=F_{5}+F_{6}=5+8=13}\end{array}$

Respuesta:

$1,1,2,3,5,8,13$

Figura 9.1.1: Leonardo Fibonacci (1170—1250)

Los números de Fibonacci aparecen en aplicaciones que van desde el arte hasta la informática y la biología. La belleza de esta secuencia se puede visualizar construyendo una espiral de Fibonacci. Considera un alicatado de cuadrados donde cada lado tenga una longitud que coincida con cada número de Fibonacci:

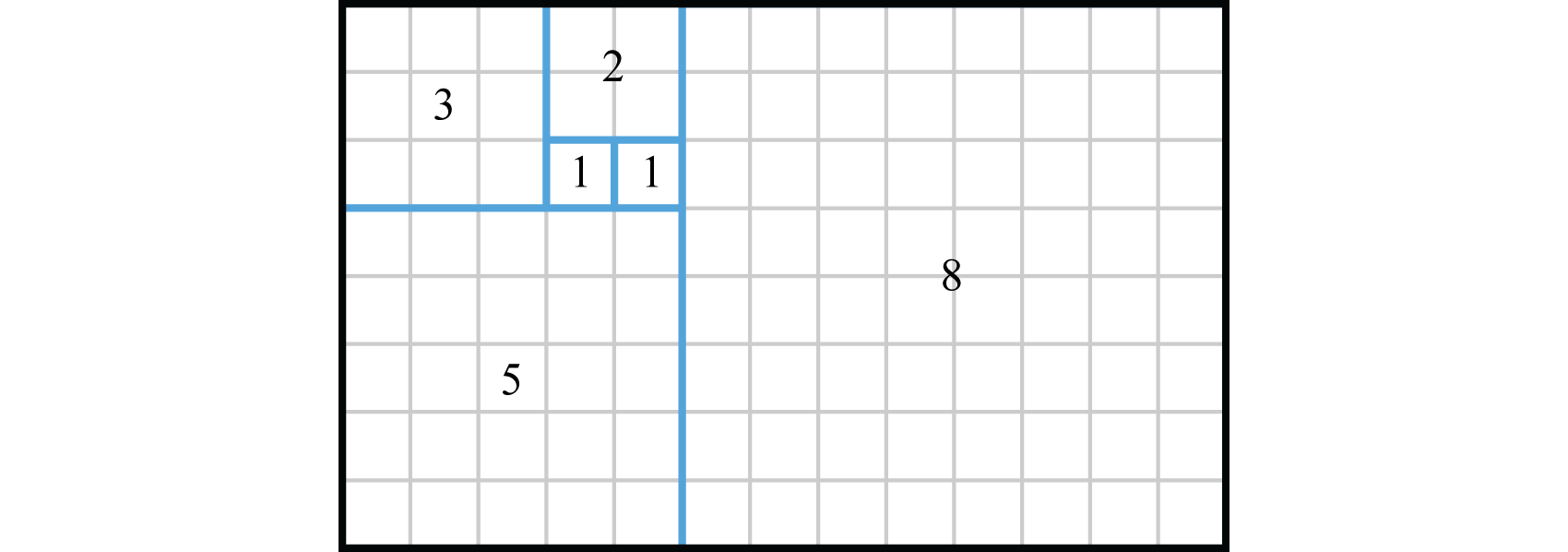
Figura 9.1.2

Conectar las esquinas opuestas de los cuadrados con un arco produce una forma espiral especial.

Figura 9.1.3

Esta forma se llama espiral de Fibonacci y se aproxima a muchas formas espirales que se encuentran en la naturaleza.

Serie

Una serie ⁶ es la suma de los términos de una secuencia. La suma de los términos de una secuencia infinita da como resultado una serie infinita ⁷, denotada$S_{∞}$. La suma de los primeros$n$ términos en una secuencia se denomina suma parcial ⁸, denotada$S_{n}$. Por ejemplo, dada la secuencia de enteros impares positivos$1, 3, 5,…$ podemos escribir:

$\begin{array}{l}{S_{\infty}=1+3+5+7+9+\dots \quad\color{Cerulean} { Infinite\: series }} \\ {S_{5}=1+3+5+7+9=25 \quad\:\:\color{Cerulean} { 5th\: partial\: sum }}\end{array}$

Ejemplo$\PageIndex{4}$:

Determinar las sumas$3^{rd}$ y$5^{th}$ parciales de la secuencia:$3,−6, 12,−24, 48,… $

Solución:

$S_{3}=3+(-6)+12=9$
$S_{5}=3+(-6)+12+(-24)+48=33$

Respuesta:

$S_{3}=9 ; S_{5}=33$

Si se conoce el término general, entonces podemos expresar una serie usando la notación sigma ⁹ (o suma ¹⁰):

$\begin{aligned}S_{\infty}&=\sum_{n=1}^{\infty} n^{2}=1^{2}+2^{2}+3^{2}+\ldots & \color{Cerulean}{Infinite\:series} \\ S_{3}&=\sum_{n=1}^{3} n^{2}=1^{2}+2^{2}+3^{2} & \color{Cerulean}{3rd\:partial\:sum}\end{aligned}$

El símbolo$\Sigma$ (letra griega mayúscula sigma) se utiliza para indicar una serie. Las expresiones arriba y abajo indican el rango del índice de suma ¹¹, en este caso representado por$n$. El número inferior indica el entero inicial y el valor superior indica el entero final. La$n$ ésima suma parcial se$S_{n}$ puede expresar usando la notación sigma de la siguiente manera:

$S_{n}=\sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+\cdots+a_{n}$

Esto se lee, “la suma de$a_{k}$ como$k$ va de$1$ a”$n$. Reemplazar$n$ con$∞$ para indicar una suma infinita.

Ejemplo$\PageIndex{5}$:

Evaluar:$\sum_{k=1}^{5}(-3)^{n-1}$.

$\begin{aligned} \sum_{k=1}^{5}(-3)^{k-1} &=(-3)^{\color{Cerulean}{1}\color{black}{-}1}+(-3)^{\color{Cerulean}{2}\color{black}{-}1}+(-3)^{\color{Cerulean}{3}\color{black}{-}1}+(-3)^{\color{Cerulean}{4}\color{black}{-}1}+(-3)^{\color{Cerulean}{5}\color{black}{-}1} \\ &=(-3)^{0}+(-3)^{1}+(-3)^{2}+(-3)^{3}+(-3)^{4} \\ &=1-3+9-27+81 \\ &=61 \end{aligned}$

Respuesta:

$61$

Cuando se trabaja con notación sigma, el índice no siempre comienza en$1$.

Ejemplo$\PageIndex{1}$:

Evaluar:$\sum_{k=2}^{5}(-1)^{k}(3 k)$

Solución:

Aquí el índice se expresa utilizando la variable$k$, que va de$2$ a$5$.

Ejercicio$\PageIndex{2}$

Evaluar:$\sum_{n=1}^{5}(15-9 n)$.

Contestar

$-60$

http://www.youtube.com/v/aZ3sPd8N1TU

El infinito se utiliza como límite superior de una suma para indicar una serie infinita.

Ejemplo$\PageIndex{7}$:

Escribir en forma expandida:$\sum_{i=0}^{\infty} \frac{n}{n+1}$.

Solución:

En este caso comenzamos con$n = 0$ y agregamos tres puntos para indicar que esta serie continúa para siempre.

$\begin{aligned} \sum_{n=0}^{\infty} \frac{n}{n+1} &=\frac{\color{Cerulean}{0}}{\color{Cerulean}{0}\color{black}{+}1}+\frac{\color{Cerulean}{1}}{\color{Cerulean}{1}\color{black}{+}1}+\frac{\color{Cerulean}{2}}{\color{Cerulean}{2}\color{black}{+}1}+\frac{\color{Cerulean}{3}}{\color{Cerulean}{3}\color{black}{+}1}+\cdots \\ &=\frac{0}{1}+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots \\ &=0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots \end{aligned}$

Respuesta:

$0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots$

Al expandir una serie, tenga cuidado de reemplazar solo la variable que indica el índice.

Ejemplo$\PageIndex{8}$:

Escribir en forma expandida:$\sum_{i=1}^{\infty}(-1)^{i-1} x^{2 i}$.

Solución:

$\begin{aligned} \sum_{i=1}^{\infty}(-1)^{i-1} x^{2 i} &=(-1)^{\color{Cerulean}{1}\color{black}{-}1} x^{2(\color{Cerulean}{1}\color{black}{)}}+(-1)^{\color{Cerulean}{2}\color{black}{-}1} x^{2(\color{Cerulean}{2}\color{black}{)}}+(-1)^{\color{Cerulean}{3}\color{black}{-}1} x^{2(\color{Cerulean}{3}\color{black}{)}}+\cdots \\ &=(-1)^{0} x^{2(1)}+(-1)^{1} x^{2(2)}+(-1)^{2} x^{2(3)}+\cdots \\ &=x^{2}-x^{4}+x^{6}-\cdots \end{aligned}$

Respuesta:

$x^{2}-x^{4}+x^{6}-\cdots$

Claves para llevar

Una secuencia es una función cuyo dominio consiste en un conjunto de números naturales que comienzan con$1$. Además, una secuencia puede pensarse como una lista ordenada.
Las fórmulas se utilizan a menudo para describir el término$n$ th, o término general, de una secuencia usando la notación subcriptada$a_{n}$.
Una serie es la suma de los términos en una secuencia. La suma de los primeros$n$ términos se llama la$n$ ésima suma parcial y se denota$S_{n}$.
Utilice la notación sigma para denotar sumas de manera compacta. La enésima suma parcial, usando notación sigma, se puede escribir$S_{n}=\sum_{k=1}^{n} a_{k}$. El símbolo$\Sigma$ denota una suma donde la expresión a continuación indica que el índice$k$ comienza en$1$ e itera a través de los números naturales que terminan con el valor$n$ anterior.

Ejercicio$\PageIndex{3}$

Encuentra los primeros$5$ términos de la secuencia así como el$30^{th}$ término.

$a_{n}=2 n$
$a_{n}=2 n+1$
$a_{n}=\frac{n^{2}-1}{2}$
$a_{n}=\frac{n}{2 n-1}$
$a_{n}=(-1)^{n}(n+1)^{2}$
$a_{n}=(-1)^{n+1} n^{2}$
$a_{n}=3^{n-1}$
$a_{n}=2^{n-2}$
$a_{n}=\left(\frac{1}{2}\right)^{n}$
$a_{n}=\left(-\frac{1}{3}\right)^{n}$
$a_{n}=\frac{(-1)^{n-1}}{3 n-1}$
$a_{n}=\frac{2(-1)^{n}}{n+5}$
$a_{n}=1+\frac{1}{n}$
$a_{n}=\frac{n^{2}+1}{n}$

Contestar

1. $2,4,6,8,10 ; a_{30}=60$

3. $0, \frac{3}{2}, 4, \frac{15}{2}, 12 ; a_{30}=\frac{899}{2}$

5. $-4,9,-16,25,-36 ; a_{30}=961$

7. $1,3,9,27,81 ; a_{30}=3^{29}$

9. $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32} ; a_{30}=\frac{1}{2^{30}}$

11. $\frac{1}{2},-\frac{1}{5}, \frac{1}{8},-\frac{1}{11}, \frac{1}{14} ; a_{30}=-\frac{1}{89}$

13. $2, \frac{3}{2}, \frac{4}{3}, \frac{5}{4}, \frac{6}{5} ; a_{30}=\frac{31}{30}$

Ejercicio$\PageIndex{4}$

Encuentra los primeros$5$ términos de la secuencia.

$a_{n}=2 x^{2 n-1}$
$a_{n}=(2 x)^{n-1}$
$a_{n}=\frac{x^{n}}{n+4}$
$a_{n}=\frac{x^{2 n}}{x-2}$
$a_{n}=\frac{n x^{2 n}}{n+1}$
$a_{n}=\frac{(n+1) x^{n}}{n^{2}}$
$a_{n}=(-1)^{n} x^{3 n}$
$a_{n}=(-1)^{n-1} x^{n+1}$

Contestar

1. $2 x, 2 x^{3}, 2 x^{5}, 2 x^{7}, 2 x^{9}$

3. $\frac{x}{5}, \frac{x^{2}}{6}, \frac{x^{3}}{7}, \frac{x^{4}}{8}, \frac{x^{5}}{9}$

5. $\frac{x^{2}}{2}, \frac{2 x^{4}}{3}, \frac{3 x^{6}}{4}, \frac{4 x^{8}}{5}, \frac{5 x^{10}}{6}$

7. $-x^{3}, x^{6},-x^{9}, x^{12},-x^{15}$

Ejercicio$\PageIndex{5}$

Encuentra los primeros 5 términos de la secuencia definida por la relación de recurrencia dada.

$a_{n}=a_{n-1}+5$donde$a_{1}=3$
$a_{n}=a_{n-1}-3$donde$a_{1}=4$
$a_{n}=3 a_{n-1}$donde$a_{1}=-2$
$a_{n}=-2 a_{n-1}$donde$a_{1}=-1$
$a_{n}=n a_{n-1}$donde$a_{1}=1$
$a_{n}=(n-1) a_{n-1}$donde$a_{1}=1$
$a_{n}=2 a_{n-1}-1$donde$a_{1}=0$
$a_{n}=3 a_{n-1}+1$donde$a_{1}=-1$
$a_{n}=a_{n-2}+2 a_{n-1}$dónde$a_{1}=-1$ y$a_{2}=0$
$a_{n}=3 a_{n-1}-a_{n-2}$dónde$a_{1}=0$ y$a_{2}=2$
$a_{n}=a_{n-1}-a_{n-2}$dónde$a_{1}=1$ y$a_{2}=3$
$a_{n}=a_{n-2}+a_{n-1}+2$dónde$a_{1}=-4$ y$a_{2}=-1$

Contestar

1. $3, 8, 13, 18, 23$

3. $−2, −6, −18, −54, −162$

5. $1, 2, 6, 24, 120$

7. $0, −1, −3, −7, −15$

9. $−1, 0, −1, −2, −5$

11. $1, 3, 2, −1, −3$

Ejercicio$\PageIndex{6}$

Encuentra el término indicado.

$a_{n}=2-7 n ; a_{12}$
$a_{n}=3 n-8 ; a_{20}$
$a_{n}=-4(5)^{n-4} ; a_{7}$
$a_{n}=6\left(\frac{1}{3}\right)^{n-6} ; a_{9}$
$a_{n}=1+\frac{1}{n}; a_{10}$
$a_{n}=(n+1) 5^{n-3} ; a_{5}$
$a_{n}=(-1)^{n} 2^{2 n-3} ; a_{4}$
$a_{n}=n(n-1)(n-2) ; a_{6}$
Se$4,500$ realiza una inversión de $ en una cuenta con$2$% de interés compuesto trimestralmente. El saldo en la cuenta después de los$n$ trimestres viene dado por$a_{n}=4500\left(1+\frac{0.02}{4}\right)^{n}$. Encuentra el monto en la cuenta después de cada trimestre de los dos primeros años. Redondear al centavo más cercano.
El valor de un auto nuevo después de$n$ años viene dado por la fórmula$a_{n}=18,000\left(\frac{3}{4}\right)^{n}$. Encontrar e interpretar$a_{7}$. Redondear al dólar entero más cercano.
El número de comparaciones que hace un algoritmo informático para ordenar n nombres en una lista viene dado por la fórmula$a_{n}=n \log _{2} n$. Determinar el número de comparaciones que se necesita este algoritmo para ordenar$2 × 10^{6}$ (2 millones) nombres.
El número de comparaciones que hace un algoritmo informático para buscar$n$ nombres en una lista viene dado por la fórmula$a_{n}=n^{2}$ Determinar el número de comparaciones que toma este algoritmo para buscar$2 × 10^{6}$ (2 millones) nombres.

Contestar

1. $-82$

3. $-500$

5. $\frac{11}{10}$

7. $32$

9. Año 1: QI: $$4,522.50$; QII: $$4,545.11$; QIII: $$4,567.84$; QIV: $$4,590.68$; Año 2: QI: $$4,613.63$; QII: $$4,636.70$; QIII: $$4,659.88$; QIV: $$4,683.18$

11. $4 \times 10^{7}$Comparaciones aproximadas

Ejercicio$\PageIndex{7}$

Encuentra la suma parcial indicada.

$3,5,9,17,33, \ldots ; S_{4}$
$-5,7,-29,79,-245, \ldots ; S_{4}$
$4,1,-4,-11,-20, \ldots ; S_{5}$
$0,2,6,12,20, \ldots ; S_{3}$
$a_{n}=2-7 n ; S_{5}$
$a_{n}=3 n-8 ; S_{5}$
$a_{n}=-4(5)^{n-4} ; S_{3}$
$a_{n}=6\left(\frac{1}{3}\right)^{n-6} ; S_{3}$
$a_{n}=1+\frac{1}{n}; S_{4}$
$a_{n}=(n+1) 5^{n-3} ; S_{3}$
$a_{n}=(-1)^{n} 2^{2 n-3} ; S_{5}$
$a_{n}=n(n-1)(n-2) ; S_{4}$

Contestar

1. $34$

3. $-30$

5. $-95$

7. $-\frac{124}{125}$

9. $\frac{73}{12}$

11. $-\frac{205}{2}$

Ejercicio$\PageIndex{8}$

Evaluar.

$\sum_{k=1}^{5} 3 k$
$\sum_{k=1}^{6} 2 k$
$\sum_{i=2}^{6} i^{2}$
$\sum_{i=0}^{4}(i+1)^{2}$
$\sum_{n=1}^{5}(-1)^{n+1} 2^{n}$
$\sum_{n=5}^{10}(-1)^{n} n^{2}$
$\sum_{k=-2}^{2}\left(\frac{1}{2}\right)^{k}$
$\sum_{k=-4}^{0}\left(\frac{1}{3}\right)^{k}$
$\sum_{k=0}^{4}(-2)^{k+1}$
$\sum_{k=-1}^{3}(-3)^{k-1}$
$\sum_{n=1}^{5} 3$
$\sum_{n=1}^{7}-5$
$\sum_{k=-2}^{3} k(k+1)$
$\sum_{k=-2}^{2}(k-2)(k+2)$

Contestar

1. $45$

3. $90$

5. $22$

7. $\frac{31}{4}$

9. $−22$

11. $15$

13. $22$

Ejercicio$\PageIndex{9}$

Escribir en forma expandida.

$\sum_{n=1}^{\infty} \frac{n-1}{n}$
$\sum_{n=1}^{\infty} \frac{n}{2 n-1}$
$\sum_{n=1}^{\infty}\left(-\frac{1}{2}\right)^{n-1}$
$\sum_{n=0}^{\infty}\left(-\frac{2}{3}\right)^{n+1}$
$\sum_{n=1}^{\infty} 3\left(\frac{1}{5}\right)^{n}$
$\sum_{n=0}^{\infty} 2\left(\frac{1}{3}\right)^{n}$
$\sum_{k=0}^{\infty}(-1)^{k} x^{k+1}$
$\sum_{k=1}^{\infty}(-1)^{k+1} x^{k-1}$
$\sum_{i=0}^{\infty}(-2)^{i+1} x^{i}$
$\sum_{i=1}^{\infty}(-3)^{i-1} x^{3 i}$
$\sum_{k=1}^{\infty}(2 k-1) x^{2 k}$
$\sum_{k=1}^{\infty} \frac{k x^{k-1}}{k+1}$

Contestar

1. $0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots$

3. $1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\cdots$

5. $\frac{3}{5}+\frac{3}{25}+\frac{3}{125}+\frac{3}{625}+\cdots$

7. $x-x^{2}+x^{3}-x^{4}+\cdots$

9. $-2+4 x-8 x^{2}+16 x^{3}-\dots$

11. $x^{2}+3 x^{4}+5 x^{6}+7 x^{8}+\cdots$

Ejercicio$\PageIndex{10}$

Exprese las siguientes series usando notación sigma.

$x+2 x^{2}+3 x^{3}+4 x^{4}+5 x^{5}$
$\frac{1}{2} x^{2}+\frac{2}{3} x^{3}+\frac{3}{4} x^{4}+\frac{4}{5} x^{5}+\frac{5}{6} x^{6}$
$2+2^{2} x+2^{3} x^{2}+2^{4} x^{3}+2^{5} x^{4}$
$3 x+3^{2} x^{2}+3^{3} x^{3}+3^{4} x^{4}+3^{5} x^{5}$
$2 x+4 x^{2}+8 x^{3}+\dots+2^{n} x^{n}$
$x+3 x^{2}+9 x^{3}+\dots+3^{n} x^{n+1}$
$5+(5+d)+(5+2 d)+\dots+(5+n d)$
$2+2 r^{1}+2 r^{2}+\dots+2 r^{n-1}$
$\frac{3}{4}+\frac{3}{8}+\frac{3}{16}+\dots+3\left(\frac{1}{2}\right)^{n}$
$\frac{8}{3}+\frac{16}{4}+\frac{32}{5}+\dots+\frac{2^{n}}{n}$
Una liquidación estructurada arroja una cantidad en dólares cada año, representada por$n$, según la fórmula$p_{n}=10,000(0.70)^{n-1}$. ¿Cuál es el monto total obtenido de la liquidación después de$5$ años?
La primera fila de asientos en un pequeño teatro consiste en$14$ asientos. Cada fila a partir de entonces consta de$2$ más asientos que la fila anterior. Si hay$7$ filas, ¿cuántos asientos totales hay en el teatro?

Contestar

1. $\sum_{k=1}^{5} k x^{k}$

3. $\sum_{k=1}^{5} 2^{k} x^{k-1}$

5. $\sum_{k=1}^{n} 2^{k} x^{k}$

7. $\sum_{k=0}^{n}(5+k d)$

9. $\sum_{k=2}^{n} 3\left(\frac{1}{2}\right)^{k}$

11. $\$ 27,731$

Ejercicio$\PageIndex{11}$

Investigar y discutir los números de Fibonacci tal como se encuentran en la naturaleza.
Investigar y discutir la vida y aportes de Leonardo Fibonacci.
Explicar la diferencia entre una secuencia y una serie. Proporcione un ejemplo de cada uno.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

¹ Una función cuyo dominio es un conjunto de números naturales consecutivos que comienzan con$1$.

² Una secuencia cuyo dominio es el conjunto de números naturales$\{1,2,3, \dots\}$.

³ Ecuación que define el término n de una secuencia comúnmente denotada usando subíndices$a_{n}$.

⁴ Una secuencia cuyo dominio es$\{1,2,3, \dots, k\}$ donde$k$ es un número natural.

⁵ Una fórmula que utiliza términos previos de una secuencia para describir términos subsiguientes.

⁶ La suma de los términos de una secuencia.

⁷ La suma de los términos de una secuencia infinita denotada$S_{∞}$.

⁸ La suma de los primeros n términos en una secuencia denotada$S_{n}$.

⁹ Una suma denotada usando el símbolo$\Sigma$ (letra griega mayúscula sigma).

¹⁰ Se utiliza cuando se refiere a la notación sigma.

¹¹ La variable utilizada en notación sigma para indicar los límites inferior y superior de la suma.