1.3: Los números racionales

Última actualización
Guardar como PDF

Page ID: 111560

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comenzamos con la definición de un número racional.

Números racionales

Cualquier número que se pueda expresar en la forma$p/q$, donde$p$ y$q$ son enteros,$q \neq 0$, se denomina número racional. La letra$\mathbb{Q}$ se utiliza para representar el conjunto de números racionales. Es decir:

\[\mathbb{Q}=\left\{\dfrac{p}{q} : p \text { and } q \text { are integers, } q \neq 0\right\} \nonumber \]

Porque$-2/3$,$4/5$, y$123/(-12)$ tener la forma$p/q$, donde$p$ y$q$ son enteros, cada uno es un ejemplo de un número racional. Si crees que escuchas la palabra “fracción” cuando decimos “número racional”, tienes razón en tu pensamiento. Cualquier número que pueda expresarse como una fracción, donde el numerador y el denominador son enteros, es un número racional. Cada entero es también un número racional. Tomemos, por ejemplo, el entero$-12$. Hay varias formas en las que podemos expresar$-12$ como una fracción con numerador entero y denominador,$-12/1$,$24/(-2)$, y$-36/3$ siendo unos pocos.

Reducción de fracciones a términos más bajos

Primero, determinamos lo que se entiende por el mayor divisor común de dos enteros.

El mayor divisor común

Dados dos enteros$a$ y$b$, el mayor divisor común de$a$ y$b$ es el entero más grande que divide uniformemente (sin resto) en ambos$a$ y$b$. La notación$\operatorname{GCD}(a, b)$ se utiliza para representar el mayor divisor común de$a$ y$b$.

Por ejemplo,$\operatorname{GCD}(12,18)=6, \operatorname{GCD}(32,40)=8,$ y$\operatorname{GCD}(18,27)=9$.

Ahora podemos afirmar cuando una fracción se reduce a los términos más bajos.

Términos más bajos

Se dice que una fracción$a/b$ se reduce a términos más bajos si y solo si$\operatorname{GCD}(a, b)=1$.

Una técnica común utilizada para reducir una fracción a términos más bajos es dividir tanto el numerador como el denominador por su mayor divisor común.

Ejemplo$\PageIndex{1}$

Reducir$8/12$ a los términos más bajos.

Solución

Tenga en cuenta que$\operatorname{GCD}(8,12)=4$. Divide tanto el numerador como el denominador por$4$.

\[\begin{aligned} \dfrac{8}{12} &=\dfrac{8 \div 4}{12 \div 4} \quad \color{Red} \text{Divide numerator and denominator by } \operatorname{GCD}(8,12)=4 \\ &=\dfrac{2}{3} \quad \color{Red} \text{Simplify numerator and denominator.}\\ \text{Thus, } 8/12 &= 2/3 \end{aligned} \nonumber\]

Ejercicio$\PageIndex{1}$

Reducir:$-48 / 60$.

Contestar: $-4 / 5$

Recordemos la definición de un número primo.

Número Primo

Un número natural mayor que uno es primo si y sólo si sus únicos divisores son uno y él mismo.

Por ejemplo,$7$ es primo (sus únicos divisores son$1$ y$7$), pero no lo$14$ es (sus divisores son$1$,$2$,$7$, y$14$). En la moda como$2$,$3$, y$5$ son prime, pero$6$,$15$, y no$21$ son prime.

Ejemplo$\PageIndex{2}$

Reducir$10/40$ a los términos más bajos.

Solución

Tenga en cuenta que$\operatorname{GCD}(10,40)=10$. Dividir numerador y denominador por$10$.

\[\begin{aligned} \dfrac{10}{40} &=\dfrac{10 \div 10}{40 \div 10} \quad \color{Red} \text{Divide numerator and denominator by } \operatorname{GCD}(10,40)=10 \\ &=\dfrac{1}{4} \quad \color{Red} \text{Simplify numerator and denominator.}\\ \text{Thus, } 10/40 &= 1/4 \end{aligned} \nonumber\]

Solución alternativa

Utilice árboles de factores para expresar tanto el numerador como el denominador como producto de factores primos.

$fig 1.3.1a.png$

Figura$\PageIndex{1}$

De ahí,$10=2 \cdot 5$ y$40=2 \cdot 2 \cdot 2 \cdot 5$. Ahora, para reducir$10/40$ a términos más bajos, reemplazar el numerador y el denominador con sus factorizaciones primos, luego cancelar los factores que son comunes tanto al numerador como al denominador.

\ [\ begin {alineado}
\ dfrac {10} {40} &=\ dfrac {2\ cdot 5} {2\ cdot 2\ cdot 2\ cdot 5}\ quad\ color {Rojo}\ texto {Numerador de factor primo y denominador.} \\
&=\ dfrac {{\ color {Rojo}\ no} 2\ cdot {\ color {Rojo}\ no} 5} {{\ color {Rojo}\ no} 2\ cdot 2\ cdot 2\ cdot {\ color {Rojo}\ no} 5}\ quad\ color {Rojo}\ texto {Cancelar factores comunes.} \\
&=\ dfrac {1} {4}\ quad\ color {Rojo}\ texto {Simplifica numerador y denominador.}
\ end {alineado}\]

Cuando cancelamos$2$ a tanto del numerador como del denominador, en realidad estamos dividiendo tanto el numerador como el denominador por$2$. Se puede hacer una declaración similar sobre la cancelación del$5$. Cancelar ambos$2$ y a$5$ equivale a dividir tanto el numerador como el denominador por$10$. Esto explica el$1$ en el numerador cuando todos los factores cancelan.

Ejercicio$\PageIndex{2}$

Reducir$18/ 24$ a los términos más bajos.

Contestar: $3/ 4$

Ejemplo $\PageIndex{2}$demuestra un punto importante.

Cuando todos los factores cancelan

Cuando todos los factores se cancelan en numerador o denominador, el numerador o denominador resultante es igual a uno.

Multiplicar fracciones

Primero, la deﬁnición.

Multiplicación de Fracciones

Si$a/b$ y$c/d$ son dos fracciones, entonces su producto se deﬁnará de la siguiente manera:

\[\dfrac{a}{b} \cdot \dfrac{c}{d}=\dfrac{a c}{b d} \nonumber \]

Así, para encontrar el producto de$a/b$ y$c/d$, simplemente multiplicar numeradores y multiplicar denominadores. Por ejemplo:

\[\dfrac{1}{2} \cdot \dfrac{3}{4}=\dfrac{3}{8} \quad \text { and } \quad -\dfrac{2}{5} \cdot \dfrac{7}{3}= -\dfrac{14}{15} \quad \text { and } \quad -\dfrac{5}{8} \cdot \left(-\dfrac{1}{6} \right)=\dfrac{5}{48} \nonumber \]

Al igual que la multiplicación entera, los signos similares producen una respuesta positiva, a diferencia de los signos dan una respuesta negativa. Por supuesto, cuando sea necesario, recuerde reducir su respuesta a los términos más bajos.

Ejemplo$\PageIndex{3}$

Simplificar:$-\dfrac{14}{20} \cdot \dfrac{10}{21}$.

Solución

Multiplique numeradores y denominadores, luego reduzca a términos más bajos.

\ [\ begin {alineado}
-\ dfrac {14} {20}\ cdot\ dfrac {10} {21} &=-\ dfrac {140} {420}\ quad\ color {Rojo}\ texto {Multiplicar numeradores y denominadores}\\
&=-\ dfrac {2\ cdot 2\ cdot 5\ cdot 7} {2\ cdot 2\ cdot 3\ cdot 5\ cdot 7}\ quad\ color {Rojo}\ texto {Factor primo.} \\
&=-\ dfrac {{\ color {rojo}\ no} 2\ cdot {\ color {rojo}\ no} 2\ cdot {\ color {rojo}\ no} 5\ cdot {\ color {rojo}\ no} 7} {{\ color {rojo}\ no} 2\ cdot {\ color {rojo}\ no} 2\ cdot 3\ cdot {\ color {Rojo}\ no} 5\ cdot {\ color {Rojo}\ no} 7}\ quad\ color {Rojo}\ texto {Cancelar factores comunes.} \\
&=-\ dfrac {1} {3}\ quad\ color {Rojo}\ texto {Simplificar.}
\ end {alineado}\ nonumber\]

Ten en cuenta que cuando todos los factores cancelan desde el numerador, te quedas con un$1$. Así,$(-14/20)\cdot (10/21) = -1/3$.

Ejercicio$\PageIndex{3}$

Simplificar:$-\dfrac{8}{9} \cdot\left(-\dfrac{27}{20}\right)$.

Contestar: $6/5$

Regla de Cancelación

Al multiplicar fracciones, cancele los factores comunes de acuerdo con la siguiente regla: “Cancelar un factor en un numerador por un factor idéntico en un denominador”.

La regla es “cancelar algo en la parte superior por algo en la parte inferior”. Así, un enfoque alternativo para multiplicar fracciones es factorizar numeradores y denominadores en su lugar, luego cancelar un factor en un numerador por un factor idéntico en un denominador.

Ejemplo$\PageIndex{4}$

Simplificar:$\dfrac{15}{8} \cdot\left(-\dfrac{14}{9}\right)$.

Solución

Factorizar numeradores y denominadores en su lugar, luego cancelar factores comunes en los numeradores para factores comunes en los denominadores.

\ [\ begin {alineado}
\ dfrac {15} {8}\ cdot\ izquierda (-\ dfrac {14} {9}\ derecha) &=\ dfrac {3\ cdot 5} {2\ cdot 2\ cdot 2}\ cdot\ izquierda (-\ dfrac {2\ cdot 7} {3\ cdot 3}\ derecha)\ quad\ color {Rojo}\ texto {Numeradores y denominadores de factores.} \\
&=\ dfrac {{\ color {rojo}\ no} 3\ cdot 5} {{\ color {rojo}\ no} 2\ cdot 2\ cdot 2}\ cdot 2}\ cdot\ izquierda (-\ dfrac {{\ color {{rojo}\ no} 2\ cdot 7} {{\ color {rojo}\ no} 3\ cdot 3}\ derecha)\ quad\ color {Rojo}\ texto {Cancelar un factor en un numerador para un factor común en un denominador.} \\
&=-\ dfrac {35} {12}\ quad\ color {Rojo}\ texto {Multiplicar numeradores y denominadores.}
\ end {alineado}\ nonumber\]

Tenga en cuenta que a diferencia de los signos producen un producto negativo. Así,$(15/8)\cdot (-14/9) = -35/12$.

Ejercicio$\PageIndex{4}$

Simplificar:$-\dfrac{6}{45} \cdot\left(-\dfrac{35}{14}\right)$

Contestar: $1/3$

Dividiendo Fracciones

Cada número racional distinto de cero tiene un inverso multiplicativo o recíproco.

El Recíproco

Si$a$ es cualquier número racional distinto de cero, entonces$1/a$ se llama el inverso multiplicativo o recíproco de$a$, y:

\[a \cdot \dfrac{1}{a}=1 \nonumber \]

Tenga en cuenta que:

\[2 \cdot \dfrac{1}{2}=1 \quad \text { and } \quad \dfrac{3}{5} \cdot \dfrac{5}{3}=1 \quad \text { and } \quad -\dfrac{4}{7} \cdot\left(-\dfrac{7}{4}\right)=1 \nonumber \]

Así, el recíproco de$2$ es$1/2$, el recíproco de$3/5$ es$5/3$, y el recíproco de$-4/7$ es$-7/4$. Tenga en cuenta que para encontrar el recíproco de un número, simplemente invierta el número (flítelo boca abajo). Ahora podemos deﬁne el cociente de dos fracciones.

División de Fracciones

Si$a/b$ y$c/d$ son dos fracciones, entonces su cociente se define de la siguiente manera:

\[\dfrac{a}{b} \div \dfrac{c}{d}=\dfrac{a}{b} \cdot \dfrac{d}{c} \nonumber \]

La definición de división anterior se resume con la frase “invertir y multiplicar”.

Ejemplo$\PageIndex{5}$

Simplificar:$-\dfrac{35}{21} \div\left(-\dfrac{10}{12}\right)$.

Solución

Invertir y multiplicar, luego factorizar en su lugar y cancelar factores comunes en un numerador para factores comunes en un denominador.

\ [\ begin {alineado}
-\ dfrac {35} {21}\ div\ izquierda (-\ dfrac {10} {12}\ derecha) &=-\ dfrac {35} {21}\ cdot\ izquierda (-\ dfrac {12} {10}\ derecha)\ quad\ color {Rojo}\ texto {Invertir y multiplicar.} \\
&=-\ dfrac {5\ cdot 7} {3\ cdot 7}\ cdot\ izquierda (-\ dfrac {2\ cdot 2\ cdot 3} {2\ cdot 5}\ derecha)\ quad\ color {Rojo}\ texto {Factor primo.} \\
&=-\ dfrac {{\ color {Rojo}\ no} 5\ cdot {\ color {Rojo}\ no} 7} {{\ color {Rojo}\ no} 3\ cdot {\ color {Rojo}\ no} 7}\ cdot\ izquierda (-\ dfrac {{\ color {\ color {Rojo}\ no} 2\ cdot 2\ cdot {\ color {Rojo}\ not} 3} {{\ color {Rojo}\ no} 2\ cdot {\ color {Rojo}\ no} 5}\ derecho)\ quad\ color {Rojo}\ texto {Cancelar factores comunes.} \\
&=\ dfrac {2} {1}\ quad\ color {Rojo}\ texto {Multiplicar numeradores y denominadores.}\\ &=2\ quad\ color {Rojo}\ texto {Simplificar.} \ end {alineado}\ nonumber\]

Tenga en cuenta que cuando todos los factores en un denominador cancelan, a$1$ permanece. Así,$(-35/21)÷(-10/12) = 2$. Tenga en cuenta también que los signos similares arrojan un resultado positivo.

Ejercicio$\PageIndex{5}$

Simplificar:$-\dfrac{4}{9} \div \dfrac{27}{81}$.

Contestar: $-4/3$

Adición de Fracciones

Primero la deﬁnición.

Adición de Fracciones

Si dos fracciones tienen un denominador en común, sumar los numeradores y colocar el resultado sobre el denominador común. En símbolos:

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \nonumber \]

Por ejemplo:

\[-\dfrac{3}{5}+\dfrac{7}{5}=\dfrac{4}{5} \quad \text { and } \quad-\dfrac{4}{3}+\left(-\dfrac{7}{3}\right)=-\dfrac{11}{3} \quad \text { and } \quad \dfrac{4}{7}+\left(-\dfrac{5}{7}\right)=-\dfrac{1}{7} \nonumber \]

Si las fracciones no poseen un denominador común, primero crea fracciones equivalentes con un mínimo denominador común, luego suma de acuerdo con la regla anterior.

Mínimo denominador común

Si las fracciones$a/b$ y$c/d$ no comparten un denominador común, el mínimo denominador común para$b$ y$d$, escrito$\mathrm{LCD}(b, d)$, se define como el número más pequeño divisible por ambos$b$ y$d$.

Ejemplo$\PageIndex{6}$

Simplificar:$-\dfrac{3}{8}+\dfrac{5}{12}$.

Solución

El denominador menos común en este caso es el número más pequeño divisible por ambos$8$ y$12$. En este caso,$\mathrm{LCD}(8,12)=24$. Primero necesitamos hacer fracciones equivalentes con un denominador común de$24$.

\[\begin{aligned} -\dfrac{3}{8}+\dfrac{5}{12} &=-\dfrac{3}{8} \cdot \dfrac{\color{Red}3}{\color{Red}3}+\dfrac{5}{12} \cdot \dfrac{\color{Red}2}{\color{Red}2} \quad \color{Red} \text{Make equivalent fraction with a common denominator of } 24 \\ &=-\dfrac{9}{24}+\dfrac{10}{24} \quad \color{Red} \text{Multiply numerators and denominators.}\\ &=\dfrac{1}{24} \quad \color{Red} \text{Add: } -9+10=1 \end{aligned} \nonumber\]

Observe cómo agregamos los numeradores en el último paso, colocando el resultado sobre el denominador común. Así,$-3/8+5/12 = 1/24$.

Ejercicio$\PageIndex{6}$

Simplificar:$-\dfrac{5}{6}+\dfrac{1}{9}$.

Contestar: $-13/18$

Orden de Operaciones

Los números racionales obedecen las mismas Reglas Orden de Operaciones que los enteros.

Reglas que guían el orden de operaciones

Al evaluar expresiones, proceda en el siguiente orden.

Evalúe las expresiones contenidas en los símbolos de agrupación primero. Si los símbolos de agrupación están anidados, evalúe la expresión en el par más interno de símbolos de agrupación primero.
Evaluar todos los exponentes que aparecen en la expresión.
Realizar todas las multiplicaciones y divisiones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.
Realizar todas las sumas y restaciones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.

Ejemplo$\PageIndex{7}$

Dado$x =2 /3$,$y = -3/5$, y$z = 10 /9$, evaluar$xy + yz$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplazará todas las ocurrencias de variables en la expresión$xy + yz$ con paréntesis abiertos. A continuación, sustituya los valores dados de las variables ($2/3$$-3/5$for$x$$y$,$10 /9$ for y for$z$) entre paréntesis abiertos.

\[\begin{aligned} x y+y z &=( )(\;\;)+(\;\;)(\;\;) \quad \color{Red} \text{Replace variables with parentheses}\\ &=\left(\dfrac{2}{3}\right)\left(-\dfrac{3}{5}\right)+\left(-\dfrac{3}{5}\right)\left(\dfrac{10}{9}\right) \quad \color{Red} \text{Substitute: } 2/3 \text{ for } x,-3/5 \text{ for } y, \text{ and } 10/9 \text{ for } z \end{aligned} \nonumber \]

Utilice las Reglas que guían el orden de operaciones para simplificar.

\ [\ begin {alineado}
&=-\ dfrac {6} {15} +\ izquierda (-\ dfrac {30} {45}\ derecha)\ quad\ color {Rojo}\ texto {Multiplicar}\\
&=-\ dfrac {2} {5} +\ izquierda (-\ dfrac {2} {3}\ derecha)\ quad\ color {Rojo}\ texto Reducir {}\\
&=-\ dfrac {2} {5}\ cdot\ dfrac {3} {3} +\ izquierda (-\ dfrac {2} {3}\ cdot\ dfrac {5} {5}\ derecha )\ quad\ color {Rojo}\ texto {Hacer fracciones equivalentes con un}\\
&=-\ dfrac {6} {15} +\ izquierda (-\ dfrac {10} {15}\ derecha)\ quad\ color {Rojo}\ text {Mínimo denominador común}\\
&=-\ dfrac {16} {15}\ quad\ color {Rojo}\ texto {Agregar}
\ end {alineado}\ nonumber\]

Por lo tanto, si$x=2 / 3, y=-3 / 5,$ y$z=10 / 9,$ entonces$x y+y z=-16 / 15$

Ejercicio$\PageIndex{7}$

Dado$a=-1 / 2, b=2 / 3$ y$c=-3 / 4$, evaluar la expresión$a+bc$ y simplificar el resultado.

Contestar: $-1$

Ejemplo$\PageIndex{8}$

Dado$x=-3/5$, evaluar$-x^{3}$.

Solución

Primero, reemplace cada ocurrencia de la variable$x$ con paréntesis abiertos, luego sustituya$-3/5$ por$x$.

\ [\ begin {alineado}
-x^ {3} &=- () ^ {3}\ quad\ color {Rojo}\ texto {Reemplazar x con paréntesis abiertos.} \\
&=-\ izquierda (-\ dfrac {3} {5}\ derecha) ^ {3}\ quad\ color {Rojo}\ texto {Sustituir -3/5 por x}\\
&=-\ izquierda (-\ dfrac {3} {5}\ derecha)\ izquierda (-\ dfrac {3} {5}\ derecha)\ izquierda (-\ dfrac {3} 5}\ derecha)\ quad\ color {Rojo}\ texto {Escribe -3/5 como factor tres veces}\\
&=-\ izquierda (-\ dfrac {27} {125}\ derecha)\ quad\ color {Rojo}\ texto {El producto de tres fracciones negativas es negativo. Multiplicar numeradores y denominadores.} \\
&=\ dfrac {27} {125}\ quad\ color {Rojo}\ texto {Lo opuesto de -27/125 es 27/125}
\ end {alineado}\ nonumber\]

De ahí,$-x^{3}=27 / 125$, dado$x=-3/5$.

Ejercicio$\PageIndex{8}$

Simplificar:$(-1 / 3)^{4}$.

Contestar: $1/81$

Ejemplo$\PageIndex{9}$

Dado$a=-4/3$ y$b=-3 / 2$, evaluar$a^{2}+2 a b-3 b^{2}$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplazará todas las ocurrencias de variables en la expresión$a^{2}+2 a b-3 b^{2}$ con paréntesis abiertos.

A continuación, sustituya los valores dados de las variables ($-4/3$$-3/2$para$a$ y para$b$) entre paréntesis abiertos.

\[\begin{aligned} a^{2}+2 a b-3 b^{2} &=(\;\; )^{2}+2(\;\; )( \;\;)-3(\; ) ^{2} \\ &=\left(-\dfrac{4}{3}\right)^{2}+2\left(-\dfrac{4}{3}\right)\left(-\dfrac{3}{2}\right)-3\left(-\dfrac{3}{2}\right)^{2} \end{aligned} \nonumber \]

A continuación, evaluar los exponentes:$(-4 / 3)^{2}=16 / 9$ y$(-3 / 2)^{2}=9 / 4$
\[=\dfrac{16}{9}+\dfrac{2}{1}\left(-\dfrac{4}{3}\right)\left(-\dfrac{3}{2}\right)-\dfrac{3}{1}\left(\dfrac{9}{4}\right) \nonumber \]

A continuación, realizar las multiplicaciones y reducir.

\[\begin{array}{l}{=\dfrac{16}{9}+\dfrac{24}{6}-\dfrac{27}{4}} \\ {=\dfrac{16}{9}+4-\dfrac{27}{4}}\end{array} \nonumber \]

Hacer fracciones equivalentes con un denominador común, luego agregar.

\[\begin{array}{l}{=\dfrac{16}{9} \cdot {\color{Red} \dfrac{4}{4}}+4 \cdot {\color{Red} \dfrac{36}{36}}-\dfrac{27}{4} \cdot {\color{Red} \dfrac{9}{9}}} \\ {=\dfrac{64}{36}+\dfrac{144}{36}-\dfrac{243}{36}} \\ {=-\dfrac{35}{36}}\end{array} \nonumber \]

Así, si$a=-4 / 3$ y$b=-3 / 2$, entonces$a^{2}+2 a b-3 b^{2}=-35 / 36$

Ejercicio$\PageIndex{9}$

Dado$x=-3 / 4$ y$y=-4 / 5$, evaluar$x^{2}-y^{2}$.

Contestar: $-31/400$

Fracciones en la Calculadora Gráfica

Siempre debemos recordar que la calculadora gráfica es una “máquina de aproximación”. En un pequeño número de situaciones, es capaz de dar una respuesta exacta, pero para la mayoría de los cálculos, lo mejor que podemos esperar es una respuesta aproximada.

Sin embargo, la calculadora da resultados precisos para operaciones que involucran fracciones, siempre y cuando no usemos fracciones con denominadores que sean demasiado grandes para que la calculadora responda con una respuesta exacta.

Ejemplo$\PageIndex{10}$

Utilice la calculadora gráfica para simplificar cada uno de los siguientesSimplifique usando la calculadora gráfica:

$\dfrac{2}{3}+\dfrac{1}{2}$
$\dfrac{2}{3} \cdot \dfrac{5}{7}$
$\dfrac{3}{5} \div \dfrac{1}{3}$

Solución

Entramos en cada expresión a su vez.

Las Reglas de Orden de Operaciones nos dicen que debemos realizar divisiones antes de adiciones. Así, la expresión$2/3+1/2$ es equivalente a:
\[\begin{aligned} 2 / 3+1 / 2 &=\dfrac{2}{3}+\dfrac{1}{2} \quad \color{Red} \text{Divide first.}\\ &=\dfrac{4}{6}+\dfrac{3}{6} \quad \color{Red} \text{Equivalent fractions with LCD.}\\ &=\dfrac{7}{6} \quad \color{Red} \text{Add.} \end{aligned} \nonumber \] Ingresa la expresión$2/3+1/2$ en tu calculadora, luego presiona la tecla ENTRAR. El resultado se muestra en la primera imagen de la Figura$\PageIndex{2}$. A continuación, presione el botón MATH, luego seleccione 1:Frac (vea la segunda imagen en la Figura$\PageIndex{2}$) y vuelva a presionar la tecla ENTRAR. Tenga en cuenta que el resultado que se muestra en la tercera imagen de la Figura$\PageIndex{2}$ coincide con la respuesta correcta de la$7/6$ encontrada arriba.

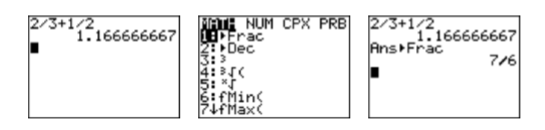
$higo 1.3.2.png$

Figura$\PageIndex{2}$: Cálculo$2/3+1/2$.

Las Reglas que guían el orden de operaciones nos dicen que no hay preferencia por la división sobre la multiplicación, o viceversa. Debemos realizar divisiones y multiplicaciones a medida que ocurren, moviéndonos de izquierda a derecha. De ahí:\ [\ begin {aligned}
2/3\ times 5/7 &=\ dfrac {2} {3}\ times 5/7\ quad\ color {Rojo}\ text {Dividir:} 2/3=\ dfrac {2} {3}\\
&=\ dfrac {10} {3}/7\ quad\ color {Rojo}\ text {Multiplicar:}\ dfrac {2} {3}\ veces 5=\ dfrac {10} {3}\
&=\ dfrac {10} {3}\ veces\ dfrac {1} {7}\ quad\ color {Rojo}\ texto {Invertir y multiplicar.} \\
&=\ dfrac {10} {21}\ quad\ color {Rojo}\ text {Multiplicar:}\ dfrac {10} {3}\ times\ dfrac {1} {7} =\ dfrac {10} {21}
\ end {alineado}\ nonumber\] Este es precisamente el mismo resultado que obtenemos cuando realizamos el siguiente cálculo. \[\dfrac{2}{3} \times \dfrac{5}{7}=\dfrac{10}{21} \quad \color{Red} \text{Multiply numerators and denominators.} \nonumber \]De ahí:\[2 / 3 \times 5 / 7 \quad \text { is equivalent to } \quad \dfrac{2}{3} \times \dfrac{5}{7} \nonumber \] Ingrese la expresión$2/3×5/7$ en su calculadora, luego presione la tecla ENTER. El resultado se muestra en la primera imagen de la Figura$\PageIndex{3}$. A continuación, presione el botón MATH, luego seleccione 1:Frac (vea la segunda imagen en la Figura$\PageIndex{3}$) y vuelva a presionar la tecla ENTRAR. Tenga en cuenta que el resultado que se muestra en la tercera imagen de la Figura$\PageIndex{3}$ coincide con la respuesta correcta de la$10/21$ encontrada arriba.

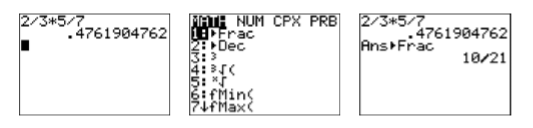
$higo 1.3.3.png$

Figura$\PageIndex{3}$: Cálculo$2/3×1/2$.

Este ejemplo demuestra que necesitamos un recordatorio constante de las Reglas que guían el orden de operaciones. Sabemos que necesitamos invertir y multiplicar en esta situación. \[\begin{aligned} \dfrac{3}{5} \div \dfrac{1}{3}&= \dfrac{3}{5} \times \dfrac{3}{1} \quad \color{Red} \text { Invert and multiply. } \\ &=\dfrac{9}{5} \quad \color{Red} \text { Multiply numerators and denominators. } \end{aligned} \nonumber \]
Entonces, la respuesta correcta es 9/5. Ingrese la expresión$3/5/1/3$ en su calculadora, luego presione la tecla ENTER. Seleccione 1:Frac en el menú MATH y vuelva a presionar la tecla ENTRAR. Tenga en cuenta que el resultado en la primera imagen de la Figura$\PageIndex{4}$ no coincide con la respuesta correcta de la$9/5$ encontrada arriba. ¿Qué hemos hecho mal? Si seguimos exactamente las Reglas Orientando el Orden de Operaciones, entonces:\ [\ begin {aligned}
3/5/1/3 & =\ dfrac {3} {5}/1/3\ quad\ color {Rojo}\ text {Dividir:} 3/5=\ dfrac {3} {5}\
& =\ dfrac {3} {5}/3\ quad\ color {Rojo}\ texto {Dividir:}\ dfrac {3} {5}/1=\ dfrac {3} {5}\\
& =\ dfrac {3} {5}\ veces\ dfrac {1} {3}\ quad\ color {Rojo}\ texto {Invertir y multiplicar.} \\
& =\ dfrac {1} {5}\ quad\ color {Rojo}\ texto {Multiplicar:}\ dfrac {3} {5}\ times\ dfrac {1} {3} =\ dfrac {1} {5}
\ end {alineado}\ nonumber\] Esto explica la respuesta que se encuentra en la primera imagen de la Figura$\PageIndex{4}$. Sin embargo, también muestra que:\[ 3 / 5 / 1 / 3 \quad \text { is not equivalent to } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \] Podemos curar el problema mediante el uso de símbolos de agrupación. \[\begin{aligned} (3 / 5) /(1 / 3) &=\dfrac{3}{5} / \dfrac{1}{3} \quad \color{Red} \text { Parentheses first. } \\ &=\dfrac{3}{5} \div \dfrac{1}{3} \quad \color{Red} \text { is equivalent to } \div \end{aligned} \nonumber \]De ahí:\[(3 / 5) /(1 / 3) \quad \text { is equivalent to } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \] Ingrese la expresión$(3/5)/(1/3)$ en su calculadora, luego presione la tecla ENTER. Seleccione 1:Frac en el menú MATH y vuelva a presionar la tecla ENTRAR. Tenga en cuenta que el resultado en la segunda imagen de la Figura$\PageIndex{4}$ coincide con la respuesta correcta de$9/5$.

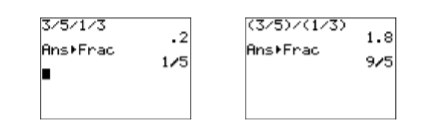
$higo 1.3.4.png$

Figura$\PageIndex{4}$: Cálculo$(3/5)/(1/3)$.

Ejercicio$\PageIndex{10}$

Simplifique el uso de la calculadora gráfica:$-\dfrac{4}{5}+\dfrac{8}{3}$.

Contestar: $28/15$

Colaboradores

Template:ContribElemAlgebraArnold