1.4: Notación decimal

Última actualización
Guardar como PDF

Page ID: 111542

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Cada número racional se puede expresar usando notación decimal. Para cambiar una fracción a su equivalente decimal, divida el numerador de la fracción por su denominador. En algunos casos el proceso terminará, dejando un resto cero. No obstante, en otros casos, los restos comenzarán a repetirse, proporcionando una representación decimal que se repite en bloques.

Ejemplo$\PageIndex{1}$

Cambia cada una de las siguientes fracciones a decimales.

$\dfrac{39}{80}$
$\dfrac{4}{11}$

Solución

Realizamos dos divisiones, la de la izquierda para cambiar$39/80$ a decimal, la de la derecha para encontrar una representación decimal para$4/11$.

$fig 1.4.1a.png$

A la izquierda, el proceso de división termina con un resto cero. De ahí,$39/80 = 0.4875$ se denomina decimal de terminación. A la derecha, los restos se repiten en un patrón y el cociente también se repite en bloques de dos. De ahí$4 / 11=0.3636 \dots$ que se llame decimal repetido. También podemos usar una barra repetitiva para escribir$4 / 11=0 . \overline{36}$. El bloque debajo de la barra de repetición se repite indeﬁnamente.

Ejercicio$\PageIndex{1}$

Cambiar$24 /7$ a un decimal.

Contestar: $3 . \overline{428571}$

Viceversa, cualquier decimal de terminación se puede expresar como una fracción. Solo necesitas contar el número de dígitos después del punto decimal y usar el mismo número de ceros en tu denominador.

Ejemplo$\PageIndex{2}$

Expresar cada uno de los siguientes decimales como fracciones. Reduzca sus respuestas a los términos más bajos.

$0.055$
$3.36$

Solución

En cada caso, cuente el número de dígitos después del punto decimal e incluya un número igual de ceros en el denominador.

En este ejemplo, hay tres dígitos después del punto decimal, por lo que colocamos el número sobre$1000$, que tiene tres ceros después del uno. \[\begin{aligned} 0.055 &=\dfrac{55}{1000} \\ &=\dfrac{11}{200} \end{aligned} \nonumber \]
En este ejemplo, hay dos dígitos después del punto decimal, por lo que colocamos el número sobre$100$, que tiene dos ceros después del uno. \[\begin{aligned} 3.36 &=\dfrac{336}{100} \\ &=\dfrac{84}{25} \end{aligned} \nonumber \]

Ejercicio$\PageIndex{2}$

Cambiar$0.45$ a una fracción. Reducir a los términos más bajos.

Contestar: $9/20$

Como vimos en Ejemplo $\PageIndex{1}$, el decimal repetido$0. \overline{36}$ es equivalente a la fracción$4/11$. En efecto, cualquier decimal repetido puede escribirse como una fracción. Por ejemplo,$0. \overline{3}=1 / 3$ y$0. \overline{142857}=1 / 7$. En futuros cursos aprenderás una técnica para cambiar cualquier decimal repetido a una fracción equivalente. Sin embargo, no todos los decimales terminan o se repiten. Por ejemplo, consideremos el decimal$0.42422422242222 \ldots$, que ni termina ni repite. Este número no se puede expresar usando la notación de barras repetitivas porque cada iteración genera una adicional$2$. Debido a que este número no se repite ni termina, no se puede expresar como una fracción. De ahí,$0.42422422242222 \ldots$ es un ejemplo de un número irracional.

Números irracionales

Si un número no se puede expresar en la forma$p/q$, donde$p$ y$q$ son enteros$q \neq 0$, entonces el número se llama un número irracional.

Números reales

Al incluir todos los números racionales e irracionales en un solo conjunto, formamos lo que se conoce como el conjunto de números reales.

El conjunto de números reales incluye cada número que usaremos en este libro de texto y curso.

Sumando y restando decimales

Al agregar decimales firmados, use las mismas reglas que aprendió a usar al agregar enteros o fracciones con signo.

Firmar reglas para la adición

Al agregar dos números decimales, use las siguientes reglas:

Para agregar dos decimales con signos similares, agregue sus magnitudes y preﬁx su signo común.
Para sumar dos decimales con signos diferentes, resta la magnitud menor de la mayor, luego preﬁx el signo del número decimal que tiene la magnitud mayor.

Ejemplo$\PageIndex{3}$

Simplificar:

$-2.3+(-0.015)$
$-8.4+6 .95$

Solución

En este problema, tenga en cuenta que tenemos señales similares. De ahí que sumemos las magnitudes y preﬁx el signo común. \[-2.3+(-0.015)=-2.315 \nonumber \]\[\begin{array}{r}{2.300} \\ {+0.015} \\ \hline 2.315\end{array} \nonumber \]
En este problema, tenga en cuenta que tenemos signos distintos. Así, primero restamos la magnitud menor de la magnitud mayor, luego preﬁx el signo del número decimal con la magnitud mayor. \[-8.4+6.95=-1.45 \nonumber\]\[\begin{array}{r}{8.40} \\ {-6.95} \\ \hline 1.45\end{array} \nonumber \]

Por lo tanto,$-2.3+(-0.015) =-2.315$ y$-8.4+6 .95 = -1.45$

Ejercicio$\PageIndex{3}$

Simplificar:$-22.6+18.47$.

Contestar: $-4.13$

La resta todavía significa “agregar lo contrario”.

Ejemplo$\PageIndex{4}$

Simplificar:

$-5.6-8.4$
$-7.9-(-5.32)$

Solución

En este problema, primero agregamos el opposito. Entonces notamos que tenemos como señales. De ahí que sumemos las magnitudes y preﬁx el signo común. \[\begin{aligned}-5.6-8.4 &=-5.6+(-8.4) \\ &=-14.0 \end{aligned} \nonumber\]\[\begin{array}{r}{5.6} \\ {+8.4} \\ \hline 14.0\end{array} \nonumber \]
En este problema, primero añadimos lo contrario. Entonces notamos que tenemos signos distintos. Así, primero restamos la magnitud menor de la magnitud mayor, luego preﬁx el signo del número decimal con la magnitud mayor. \[\begin{aligned}-7.9-(-5.32) &=-7.9+5.32 \\ &=-2.58 \end{aligned} \nonumber\]\[\begin{array}{r}{7.90} \\ {-5.32} \\ \hline 2.58\end{array} \nonumber \]

De ahí,$-5.6-8.4=-14.0$ y$-7.9-(-5.32) = -2.58$.

Ejercicio$\PageIndex{4}$

Simplificar:$-22.6-18.47$.

Contestar: $-41.07$

Multiplicación y división de decimales

Las reglas de signo para multiplicación decimal y división son las mismas que las reglas de signo utilizadas para enteros y fracciones.

Signo Reglas para multiplicación y división

Al multiplicar o dividir dos números decimales, utilice las siguientes reglas:

Los signos similares dan un resultado positivo
A diferencia de los signos dan un resultado negativo

La multiplicación de los números decimales es bastante sencilla. Primero multiplique las magnitudes de los números, ignorando los puntos decimales, luego cuente el número de dígitos a la derecha del punto decimal en cada factor. Coloque el punto decimal en el producto de manera que el número de dígitos a la derecha de los puntos decimales sea igual a la suma del número de dígitos a la derecha del punto decimal en cada factor.

Ejemplo$\PageIndex{5}$

Simplificar:$(-1.96)(2.8)$.

Solución

Multiplicar las magnitudes. El primer número decimal tiene dos dígitos a la derecha del punto decimal, el segundo tiene un dígito a la derecha del punto decimal. Así, debemos colocar un total de tres dígitos a la derecha del punto decimal en el producto.

\[(-1.96)(2.8)=-5.488 \nonumber \]

\[\begin{array}{r}{1.96} \\ { \times 2.8} \\ \hline 1568 \\ {392\;\;} \\ \hline 5.488\end{array} \nonumber \]

Tenga en cuenta que a diferencia de los signos producen un producto negativo.

Ejercicio$\PageIndex{5}$

Simplificar:$(-12.5)(-23.4)$.

Contestar: $292.50$

Al dividir números decimales firmados, ignore los signos y divida las magnitudes. Empuje el punto decimal en el divisor hasta el final del divisor, luego mueva el punto decimal en el dividendo un número igual de espacios. Esto establece el punto decimal en el cociente.

Ejemplo$\PageIndex{6}$

Simplificar:$-4.392 \div(-0.36)$.

Solución

Dividir las magnitudes. Mueve el decimal en el divisor hasta el final del divisor. Mueve el decimal en el dividendo un número igual de lugares (dos lugares) a la derecha.

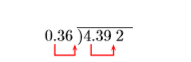
$fig 1.4.1b.png$

Coloque el punto decimal en el cociente directamente encima de la nueva posición del punto decimal en el dividendo, luego divida.

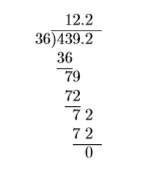
$fig 1.4.1c.png$

Los signos similares arrojan un resultado positivo. De ahí,$-4.392 \div(-0.36)=12.2$.

Ejercicio$\PageIndex{6}$

Simplificar:$-5.76 / 3.2$.

Contestar: $-1.8$

Orden de Operaciones

Los números decimales obedecen al mismo Orden de Operaciones Rector de las Reglas que los enteros y las fracciones.

Reglas que guían el orden de operaciones

Al evaluar expresiones, proceda en el siguiente orden.

Evalúe las expresiones contenidas en los símbolos de agrupación primero. Si los símbolos de agrupación están anidados, evalúe la expresión en el par más interno de símbolos de agrupación primero.
Evaluar todos los exponentes que aparecen en la expresión.
Realizar todas las multiplicaciones y divisiones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.
Realizar todas las sumas y restaciones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.

Ejemplo$\PageIndex{7}$

Dado$x=-0.12$, evaluar$-x^{2}$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplace todas las ocurrencias de la variable$x$ en la expresión$-x^2$ con paréntesis abiertos. A continuación, sustituya$-0.12$ entre paréntesis abiertos, luego simplifique.$x$

\[\begin{aligned} -x^{2} &=-(\quad)^{2} \quad \color{Red} \text { Replace } x \text { with open parentheses. } \\ &=-(-0.12)^{2} \quad \color{Red} \text { Substitute }-0.12 \text { for } x . \\ &=-(0.0144) \quad \color{Red} \text { Exponent: }(-0.12)^{2}=0.0144 \\ &=-0.0144 \quad \color{Red} \text { Negate. } \end{aligned} \nonumber \]

Tenga en cuenta que cuadramos primero, luego negamos segundo. Así, si$x = -0.12$, entonces$-x^{2}=-0.0144$.

Ejercicio$\PageIndex{7}$

Dado$y=-0.2$, evaluar:$-y^{4}$.

Contestar: $-0.0016$

Ejemplo$\PageIndex{8}$

Dado$x=-0.3$, evaluar$1.2 x^{2}-3.4 x$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplace todas las ocurrencias de la variable$x$ en la expresión$1.2 x^{2}-3.4 x$ con paréntesis abiertos. A continuación, sustituya$-0.3$ entre paréntesis abiertos, luego simplifique.$x$

\[\begin{aligned} 1.2 x^{2}-3.4 x &=1.2(\quad)^{2}-3.4(\quad) \quad \color{Red} \text { Replace } x \text { with parentheses. } \\ &=1.2(-0.3)^{2}-3.4(-0.3) \quad \color{Red} \text { Substitute }-0.3 \text { for } x . \\ &=1.2(0.09)-3.4(-0.3) \quad \color{Red} \text { Exponent: }(-0.3)^{2}=0.09 \\ &=0.108-(-1.02) \quad \color{Red} \text { Multiply: } 1.2(0.09)=0.108 \text { and } \\ &=0.108+1.02 \quad \color{Red} \text { Add the opposite. } \\ &=1.128 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Así, si$x = -0.3$, entonces$1.2 x^{2}-3.4 x=1.128$.

Ejercicio$\PageIndex{8}$

Dado$y=-0.15$,$\text { evaluate: } -1.4 y^{2}+2.2 y $.

Contestar: $-0.3615$

Vimos antes que podemos cambiar una fracción a un decimal dividiendo.

Ejemplo$\PageIndex{9}$

Dado$x=2 / 5$, evaluar$-3.2 x+5$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplace todas las ocurrencias de la variable$x$ en la expresión$-3.2x+5$ con paréntesis abiertos. A continuación, sustituya$2/5$ entre paréntesis abiertos.$x$

\[\begin{aligned} -3.2 x+5 &=-3.2(\; )+5 \quad \color{Red} \text { Replace } x \text { with open parentheses. } \\ &=-3.2\left(\dfrac{2}{5}\right)+5 \quad \color{Red} \text { Substitute } 2 / 5 \text { for } x \end{aligned} \nonumber \]

Un enfoque es cambiar$2/5$ a un decimal dividiendo el numerador por el denominador. Por lo tanto,$2/5=0 .4$.

\[\begin{aligned} &=-3.2(0.4)+5 \quad \color{Red} {\text { Replace } 2 / 5 \text { with } 0.4} \\ &=-1.28+5 \quad \color{Red} \text { Multiply: }-3.2(0.4)=-1.28 \\ &=3.72 \quad \color{Red} \text { Add: }-1.28+5=3.72 \end{aligned} \nonumber \]

Así, si$x =2 /5$, entonces$-3.2x+5=3 .72$.

Ejercicio$\PageIndex{9}$

Dado$y=-3 / 4$, evaluar$-2.3 y+7$.

Contestar: $8.725$

Como vimos en Ejemplo $\PageIndex{2}$, podemos cambiar fácilmente un decimal de terminación en una fracción colocando el número (sin el punto decimal) sobre la potencia adecuada de diez. La elección de la potencia de diez debe coincidir con el número de dígitos a la derecha del punto decimal. Por ejemplo:

\[0.411=\dfrac{411}{1000} \quad \text { and } \quad 3.11=\dfrac{311}{100} \quad \text { and } \quad 15.1111=\dfrac{151111}{10000} \nonumber \]

Tenga en cuenta que el número de ceros en cada denominador coincide con el número de dígitos a la derecha del punto decimal.

Ejemplo$\PageIndex{10}$

Dado$y =-0.25$, evaluar$-\dfrac{3}{5} y+4$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplace todas las ocurrencias de la variable$y$ en la expresión$-(3/5)y+4$ con paréntesis abiertos. A continuación, sustituya$-0.25$ entre paréntesis abiertos.$y$

\[\begin{aligned} -\dfrac{3}{5} y+4 &=-\dfrac{3}{5}(\quad)+4 \quad \color{Red} \text { Replace } y \text { with open parentheses. } \\ &=-\dfrac{3}{5}(-0.25)+4 \quad \color{Red} \text { Substitute }-0.25 \text { for } y \end{aligned} \nonumber \]

Colocar$25$ sobre$100$ para determinar eso$-0.25 = -25/100$, o después de la reducción,$-0.25 =-1/4$.

\ [\ begin {alineado}
&=-\ dfrac {3} {5}\ izquierda (-\ dfrac {1} {4}\ derecha) +4\ quad\ color {Rojo}\ texto {Reemplazar} -0.25\ texto {con} -1/4\
&=\ dfrac {3} {20} +4\ quad\ color {Rojo}\ texto {Multiplicar:} -\ dfrac {3} +4\ quad\ color {Rojo}\ texto {Multiplicar:} -\ dfrac {3}} {5}\ izquierda (-\ dfrac {1} {4}\ derecha) =\ dfrac {3} {20}\\
&=\ dfrac {3} {20} +\ dfrac {80} {20}\ quad\ color {Rojo}\ texto {Hacer fracciones equivalentes con LCD.}\\
&=\ dfrac {83} {20}\ quad\ color {Rojo}\ texto {Agregar.}
\ end {alineado}\ nonumber\]

Así, si$y =-0.25$, entonces$-(3 / 5) y+4=83 / 20$.

Ejercicio$\PageIndex{10}$

Dado$z=-0.4$, evaluar:$5-\dfrac{4}{5} z$.

Contestar: $133/25$

Redondeo usando la calculadora gráfica

Aquí está el algoritmo para redondear un número decimal a un lugar determinado.

Reglas para redondeo

Para redondear un número a un lugar en particular, siga estos pasos:

Marque el lugar al que desea redondear. El dígito en este lugar se llama dígito de redondeo.
Marque el dígito en el lugar a la derecha inmediata del dígito de redondeo. Esto se llama el dígito de prueba.
1. Si el dígito de prueba es mayor o igual a$5$, agregue$1$ al dígito de redondeo y luego reemplace todos los dígitos a la derecha del dígito de redondeo con ceros. Los ceros finales a la derecha del punto decimal pueden ser eliminados.
2. Si el dígito de prueba es menor que$5$, mantenga el dígito de redondeo igual, luego reemplace todos los dígitos a la derecha del dígito de redondeo por ceros. Los ceros finales a la derecha del punto decimal pueden ser eliminados.

Ejemplo$\PageIndex{11}$

Utilice su calculadora gráfica para evaluar$125 x^{3}-17.5 x+44.8$ en$x = -3.13$. Redondea tu respuesta a la décima más cercana.

Solución

Primero, almacene$-3.13$ en la variable$X$ con las siguientes pulsaciones de teclas.

$fig 1.4.1d.png$

El resultado se muestra en la primera imagen de la Figura$\PageIndex{1}$. A continuación, ingrese la expresión$125 x^{3}-17.5 x+44.8$ con las siguientes pulsaciones de teclas.

$fig 1.4.1e.png$

El resultado se muestra en la segunda imagen de la Figura$\PageIndex{1}$. Así, la respuesta es aproximadamente$-3733.462125$. Ahora necesitamos redondear esta respuesta a la décima más cercana. Marque el dígito de redondeo en el lugar décimas y el dígito de prueba a su derecha inmediata.

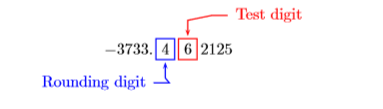
$fig 1.4.1f.png$

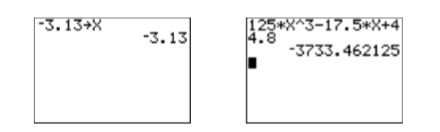
$higo 1.4.1.png$

Figura$\PageIndex{1}$: Evaluar$125 x^{3}-17.5 x+44.8$ en$x=-3.13$

Debido a que el dígito de prueba es mayor o igual a$5$, agregue$1$ al dígito de redondeo, luego reemplace todos los dígitos a la derecha del dígito de redondeo con ceros.

\[-3733.462125 \approx-3733.500000 \nonumber \]

Eliminar los ceros finales del final de la parte fraccionaria de un decimal. Esto no cambia el valor de nuestra respuesta.

\[-3733.462125 \approx-3733.5 \nonumber \]

Por lo tanto, si$x =-3.13$. entonces a la décima más cercana:

\[125 x^{3}-17.5 x+44.8 \approx-3733.5 \nonumber \]

Ejercicio$\PageIndex{11}$

Evaluar$x^{3}-3 x$ en$x =-1.012$. Redondear a la centésima más cercana.

Contestar: $2.0$

Colaboradores

Template:ContribElemAlgebraArnold