3.1: Graficar ecuaciones a mano

Última actualización
Guardar como PDF

Page ID: 111541

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comenzamos con la deﬁnición de un par ordenado.

Par Pedido

El constructo$(x,y)$, donde$x$ y$y$ son los números reales, se llama par ordenado de números reales.

$(4,3)$,$(−3,4)$$(−2,−3)$, y$(3,−1)$ son ejemplos de pares ordenados.

Asuntos de orden

Preste especial atención a la frase “pares ordenados”. Cuestiones de orden. En consecuencia, el par ordenado no$(x,y)$ es lo mismo que el par ordenado$(y,x)$, porque los números se presentan en un orden diferente.

El sistema de coordenadas cartesianas

En la Figura$\PageIndex{1}$ se muestra un Sistema de Coordenadas Cartesianas. En una cuadrícula, hemos creado dos líneas reales, una horizontal etiquetada$x$ (nos referiremos a esta como el$x$ eje -), y la otra vertical etiquetada$y$ (nos referiremos a ésta como el$y$ eje -).

higo 3.1.1.png — Figura$\PageIndex{1}$: El sistema de coordenadas cartesianas.

Dos puntos importantes:

Aquí hay dos puntos importantes a hacer sobre los ejes horizontal y vertical en la Figura$\PageIndex{1}$.

A medida que se mueve de izquierda a derecha a lo largo del eje horizontal (el$x$ eje -en la Figura$\PageIndex{1}$), los números crecen más grandes. La dirección positiva es hacia la derecha, la dirección negativa es hacia la izquierda.
A medida que se mueve de abajo hacia arriba a lo largo del eje vertical (el$y$ eje -en la Figura$\PageIndex{1}$), los números crecen más. La dirección positiva es hacia arriba, la dirección negativa es hacia abajo.

Comentarios adicionales:

higo 3.1.2.png — Figura$\PageIndex{2}$: Numerar los cuadrantes e indicar las coordenadas del origen.

Dos comentarios adicionales están en orden:

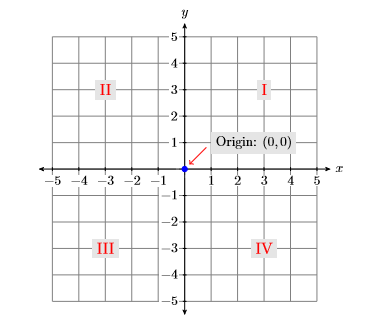
El punto donde se cruzan los ejes horizontal y vertical en la Figura$\PageIndex{2}$ se denomina origen del sistema de coordenadas. El origen tiene coordenadas$(0,0)$.
Los ejes horizontal y vertical dividen el plano en cuatro cuadrantes, numerados$\mathrm{I}, \mathrm{II}, \mathrm{MI},$ y$\mathrm{IV}$ (números romanos para uno, dos, tres y cuatro), como se muestra en la Figura$\PageIndex{2}$. Tenga en cuenta que los cuadrantes están numerados en orden antihorario.

Nota

René Descartes (1596-1650) fue un filósofo y matemático francés que es bien conocido por la famosa frase “cogito ergo sum” (creo, por lo tanto soy), que aparece en su Discurs de la methode pour bien conduire sa raison, et chercher la verite dans les sciences (Discurso sobre el método de conducir correctamente la razón y buscar la verdad en las ciencias). En ese mismo tratado, Descartes introduce su sistema de coordenadas, un método para representar puntos en el plano a través de pares de números reales. En efecto, el plano cartesiano de la actualidad se llama así en honor a René Descartes, a quien algunos llaman el “Padre de las Matemáticas Modernas”

Trazado de pares ordenados

Antes de poder trazar algún punto o dibujar alguna gráfica, ¿primero necesitamos configurar un Sistema de Coordenadas Cartesianas en una hoja de papel cuadriculado? ¿Cómo hacemos esto? ¿Qué se requiere?

cómo configurar el sistema de coordenadas cartesianas

Dibuje y etiquete cada eje.

Si vamos a trazar puntos (x, y), entonces, en una hoja de papel cuadriculado, realizar cada una de las siguientes tareas iniciales.

Usa una regla para dibujar los ejes horizontal y vertical.
Etiquete el eje horizontal como el$x$ eje -y el eje vertical como el$y$ eje -eje.

No siempre etiquetamos el eje horizontal como$x$-axis and the vertical axis as the $y$-axis. For example, if we want to plot the velocity of an object as a function of time, then we would be plotting points $(t,v)$. In that case, we would label the horizontal axis as the $t$-axis and the vertical axis as the $v$-axis.

Indicar la escala en cada eje.

Marque al menos una cuadrícula vertical con su valor numérico.
Marque al menos una cuadrícula horizontal con su valor numérico.

Las escalas en los ejes horizontal y vertical pueden variar. Sin embargo, en cada eje, la escala debe permanecer consistente. Es decir, como se cuenta a la derecha desde el origen en el$x$-axis, if each gridline represents one unit, then as you count to the left from the origin on the $x$-axis, each gridline must also represent one unit. Similar comments are in order for the $y$-axis, where the scale must also be consistent, whether you are counting up or down.

El resultado de este primer paso se muestra en la Figura$\PageIndex{3}$.

higo 3.1.3.png — Figura$\PageIndex{3}$ : Dibuje y etiquete cada eje.

Un ejemplo se muestra en la Figura$\PageIndex{4}$. Tenga en cuenta que la escala indicada en el$x$ eje -indica que cada línea de cuadrícula cuenta como$1$ -unidad a medida que contamos de izquierda a derecha. La escala en el$y$ eje -indica que cada línea de cuadrícula cuenta como$2$ -unidades a medida que contamos de abajo hacia arriba.

higo 3.1.4.png — Figura$\PageIndex{4}$ : Indicar la escala en cada eje.

Ahora que sabemos cómo configurar un Sistema de Coordenadas Cartesianas en una hoja de papel cuadriculado, aquí hay dos ejemplos de cómo trazamos puntos en nuestro sistema de coordenadas.

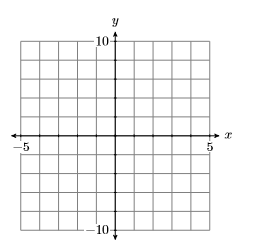
Para trazar el par ordenado$(4,3)$, comience en el origen y mueva$4$ las unidades hacia la derecha a lo largo del eje horizontal, luego$3$ las unidades hacia arriba en la dirección del eje vertical.

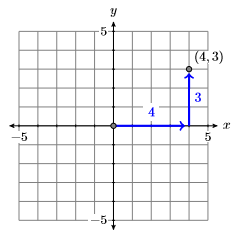
higo 3.1.5.png — Figura$\PageIndex{5}$ : Gráfica de$(4,3)$.

Para trazar el par ordenado$(−2,−3)$, comience en el origen y mueva$2$ las unidades hacia la izquierda a lo largo del eje horizontal, luego$3$ las unidades hacia abajo en dirección al eje vertical.

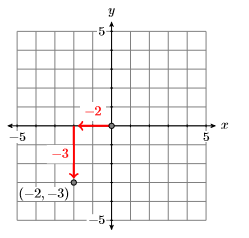
higo 3.1.6.png — Figura$\PageIndex{6}$ : Gráfica de$(-2,-3)$

Continuando de esta manera, cada par ordenado$(x,y)$ de números reales se asocia con un punto único en el plano cartesiano. Viceversa, cada punto en el punto cartesiano está asociado con un par ordenado único de números reales. Debido a esta asociación, comenzamos a usar las palabras “punto” y “par ordenado” como expresiones equivalentes, refiriéndose a veces al “punto”$(x,y)$ y otras veces al “par ordenado”$(x,y)$.

Ejemplo$\PageIndex{1}$

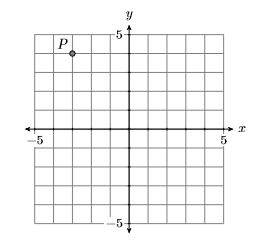
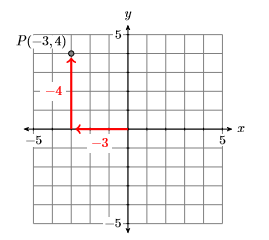
Identificar las coordenadas del punto$P$ en la Figura$\PageIndex{7}$.

higo 3.1.7.png — Figura$\PageIndex{7}$ : Identificar las coordenadas del punto$P$.

Solución

En Figura$\PageIndex{8}$, comience por el origen, mueva$3$ unidades hacia la izquierda y$4$ unidades hacia arriba para llegar al punto$P$. Esto indica que las coordenadas del punto$P$ son$(−3,4)$.

higo 3.1.8.png — Figura$\PageIndex{8}$ : Comience por el origen, mueva las$3$ unidades a la izquierda y$4$ las unidades hacia arriba.

Ejercicio$\PageIndex{1}$

Identifica las coordenadas del punto$P$ en la gráfica siguiente.

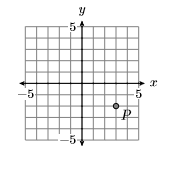
$Ejercicio 3.1.1.png$

Contestar: $(3,-2)$

Ecuaciones en dos variables

Nota

Las variables no tienen que estar siempre$x$ and $y$. For example, the equati encendidas$v =2+3 .2t$ es una ecuación en dos variables,$v$ and $t$.

La ecuación$y = x + 1$ es una ecuación en dos variables, en este caso$x$ y$y$. Considera el punto$(x,y) = (2 ,3)$. Si sustituimos$2$ por$x$ y$3$ para$y$ en la ecuación$y = x + 1$, obtenemos el siguiente resultado:

\[\begin{aligned} y &= x+1 \quad \color {Red} \text { Original equation. } \\ 3 &= 2+1 \quad \color {Red} \text { Substitute: } 2 \text { for } x, 3 \text { for } y \\ 3 &= 3 \quad \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Debido a que la última línea es una afirmación verdadera, decimos que$(2,3)$ es una solución de la ecuación$y = x + 1$. Como alternativa, decimos que$(2,3)$ satisface la ecuación$y = x + 1$. Por otra parte, considera el punto$(x,y)=(−3,1)$. Si sustituimos$−3$ por$x$ y$1$ para$y$ en la ecuación$y = x + 1$, obtenemos el siguiente resultado.

\[\begin{aligned} y &= x+1 \quad \color {Red} \text { Original equation. } \\ 1 &= -3+1 \quad \color {Red} \text { Substitute: } -3 \text { for } x, 1 \text { for } y \\ 1 &= -2 \quad \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Debido a que la última línea es una declaración falsa, el punto no$(−3,1)$ es una solución de la ecuación$y = x+1$; es decir, el punto$(−3,1)$ no satisface la ecuación$y = x + 1$.

Soluciones de una ecuación en dos variables

Dada una ecuación en las variables$x$ y$y$ y un punto$(x,y)=(a,b)$, si al subsituar$a$ para$x$ y$b$ para$y$ una declaración verdadera resulta, entonces$(x,y)=(a,b)$ se dice que el punto es una solución de la ecuación dada. Como alternativa, decimos que el punto$(x,y)=(a,b)$ satisface la ecuación dada.

Ejemplo$\PageIndex{2}$

¿Cuál de los pares ordenados$(0,−3)$ y$(1,1)$ satisface la ecuación$y =3x−2$?

Solución

Sustituir los pares ordenados$(0,−3)$ y$(1,1)$ en la ecuación$y =3x−2$ conduce a los siguientes resultados:

Considerar$(x,y) = (0 ,−3)$. Sustituto$x$ y$0$$−3$ para$y$:

\[\begin{aligned} y &=3 x-2 \\-3 &=3(0)-2 \\-3 &=-2 \end{aligned} \nonumber \]

La declaración resultante es falsa.

Considerar$(x,y) = (1 ,1)$. Sustituto$x$ y$1$$1$ para$y$:

\[\begin{aligned} y &=3x-2 \\ 1 &=3(1)-2 \\ 1 &=1 \end{aligned} \nonumber\]

La afirmación resultante es verdadera.

Así, el par ordenado$(0,−3)$ no satisface la ecuación$y =3 x−2$, pero el par ordenado$(1 ,1)$ sí satisface la ecuación$y =3x−2$.

Ejercicio$\PageIndex{2}$

¿Cuál de los pares ordenados?$(−1,3)$ and $(2,1)$ satisfy the equation $y =2x + 5$?

Contestar: $(-1,3)$

Gráfica de ecuaciones en dos variables

Primero determinemos lo que se entiende por la gráfica de una ecuación en dos variables.

La gráfica de una ecuación

La gráfica de una ecuación es el conjunto de todos los puntos que satisfacen la ecuación dada.

Ejemplo$\PageIndex{3}$

Esbozar la gráfica de la ecuación$y = x + 1$.

Solución

La definición requiere que trazemos todos los puntos del Sistema de Coordenadas Cartesianas que satisfagan la ecuación$y = x + 1$. Primero creemos una tabla de puntos que satisfagan la ecuación. Comience creando tres columnas con encabezados$x$, y$y$$(x,y)$, luego seleccione algunos valores para$x$ y colóquelos en la primera columna.

Tome el primer valor de$x$, es decir$x = −3$, y sumételo en la ecuación$y = x + 1$.

\[\begin{aligned}y &=x+1 \\ y &=-3+1 \\ y &=-2\end{aligned} \nonumber \]

\[\begin{array}{|c|c|c|c|}\hline x & {y=x+1} & {(x, y)} \\ \hline-3 & {-2} & {(-3,-2)} \\ -2 & {} & {} \\ {-1} & {} & {} \\ { 0} & {} & {}\\ {1} & {} & {}\\ {2} & {} & {}\\ {3} & {} &{} \\ \hline\end{array} \nonumber \]

Así, cuando$x = −3$, tenemos$y = −2$. Ingresa este valor en la tabla.

Continuar sustituyendo cada valor tabular de$x$ en la ecuación$y = x + 1$ y utilizar cada resultado para completar las entradas correspondientes en la tabla.

\[\begin{array}{l}{y=-3+1=-2} \\ {y=-2+1=-1} \\ {y=-1+1=0} \\ {y=0+1=1} \\ {y=1+1=2} \\ {y=2+1=3} \\ {y=3+1=4}\end{array} \nonumber \]

\[\begin{array}{|c|c|c|c|}\hline x & {y=x+1} & {(x, y)} \\ \hline-3 & {-2} & {(-3,-2)} \\ -2 & {-1} & {(-2,-1)} \\ {-1} & {0} & {(-1,0)} \\ { 0} & {1} & {(0,1)}\\ {1} & {2} & {(1,2)}\\ {2} & {3} & {(2,3)}\\ {3} & {4} &{(3,4)} \\ \hline\end{array} \nonumber \]

La última columna de la tabla contiene ahora siete puntos que satisfacen la ecuación$y = x+1$. Trazar estos puntos en un Sistema de Coordenadas Cartesianas (ver Figura$\PageIndex{9}$).

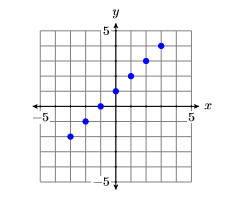
higo 3.1.9.png — Figura$\PageIndex{9}$ : Siete puntos que satisfacen la ecuación$y = x + 1$.

En la Figura$\PageIndex{9}$, hemos trazado siete puntos que satisfacen la ecuación dada$y = x+1$. Sin embargo, la definición requiere que trazemos todos los puntos que satisfagan la ecuación. Parece que se está desarrollando un patrón en Figura$\PageIndex{9}$, pero calculemos y trazemos algunos puntos más para estar seguros. Agregue los$x$ valores$−2.5$$−1.5$ -,$−0.5$,$0.5$$1.5$, y$2.5$ a la columna x de la tabla, luego use la ecuación$y = x + 1$ para evaluar y en cada uno$x$ de estos valores.

\[\begin{array}{l}{y=-2.5+1=-1.5} \\ {y=-1.5+1=-0.5} \\ {y=-0.5+1=0.5} \\ {y=0.5+1=1.5} \\ {y=1.5+1=2.5} \\ {y=2.5+1=3.5}\end{array} \nonumber \]

\[\begin{array}{|c|c|c|c|}\hline x & {y=x+1} & {(x, y)} \\ \hline-2.5 & {-1.5} & {(-2.5,-1.5)} \\ -1.5 & {-0.5} & {(-1.5,-0.5)} \\ {-0.5} & {0.5} & {(-0.5,0.5)} \\ { 0.5} & {1.5} & {(0.5,1.5)}\\ {1.5} & {2.5} & {(1.5,2.5)}\\ {2.5} & {3.5} & {(2.5,3.5)}\\ \hline\end{array} \nonumber \]

Agregue estos puntos adicionales a la gráfica de la Figura$\PageIndex{9}$ para producir la imagen mostrada en la Figura$\PageIndex{10}$.

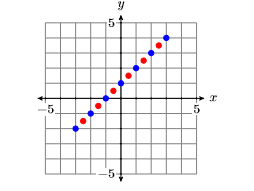
higo 3.1.10.png — Figura$\PageIndex{10}$ : Sumando puntos adicionales a la gráfica de$y = x + 1$.

Hay un número inﬁnito de puntos que satisfacen la ecuación$y = x + 1$. En Figura$\PageIndex{10}$, hemos trazado solo$13$ puntos que satisfacen la ecuación. Sin embargo, la colección de puntos trazados en la Figura$\PageIndex{10}$ sugiere que si tuviéramos que trazar el resto de los puntos que satisfacen la ecuación$y = x + 1$, obtendríamos la gráfica de la línea que se muestra en la Figura$\PageIndex{11}$.

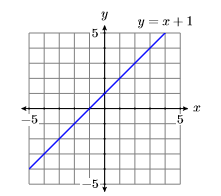
higo 3.1.11.png — Figura$\PageIndex{11}$ : La gráfica de$y = x + 1$ es una línea.

Ejercicio$\PageIndex{3}$

Esbozar la gráfica de la ecuación$y = −x + 2$.

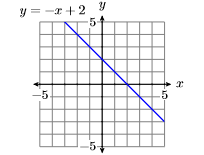
Contestar: $Ejercicio 3.1.3.png$

Lineamientos y Requerimientos

El ejemplo$\PageIndex{3}$ sugiere que debemos usar las siguientes pautas al bosquejar la gráfica de una ecuación.

Lineamientos para dibujar la gráfica de una ecuación

Cuando se le pida que dibuje la gráfica de una ecuación, realice cada uno de los siguientes pasos:

Configure y calcule una tabla de puntos que satisfagan la ecuación dada.
Configura un Sistema de Coordenadas Cartesianas en papel cuadriculado y traza los puntos de tu tabla en el sistema. Etiquete cada eje (generalmente$x$ y$y$) e indique la escala en cada eje.
Si el número de puntos trazados es suficiente para imaginar cuál será la forma de la curva final, entonces dibuje los puntos restantes que satisfagan la ecuación como se imaginó. Usa una regla si crees que la gráfica es una línea. Si la gráfica parece ser una curva, a mano alzada la gráfica sin el uso de una regla.
Si el número de puntos trazados no proporciona suficiente evidencia para visualizar la forma final de la gráfica, agregue más puntos a su tabla, grácalos e intente nuevamente imaginar la forma final de la gráfica. Si aún no puedes predecir la forma eventual de la gráfica, sigue agregando puntos a tu tabla y trazándolos hasta que estés convencido de la forma final de la gráfica.

Aquí hay algunos requisitos adicionales que deben seguirse al bosquejar la gráfica de una ecuación.

Papel cuadriculado, líneas, curvas y reglas.

Los siguientes son requisitos para esta clase:

Todas las gráficas deben ser dibujadas en papel cuadriculado.
Todas las líneas deben dibujarse con una regla. Esto incluye los ejes horizontal y vertical.
Si la gráfica de una ecuación es una curva en lugar de una línea, entonces la gráfica debe dibujarse a mano alzada, sin la ayuda de una regla.

Uso de la función TABLE de la calculadora gráfica

A medida que las ecuaciones se vuelven más complicadas, puede llegar a ser bastante tedioso crear tablas de puntos que satisfagan la ecuación. Afortunadamente, la calculadora gráfica tiene una función TABLE que le permite construir fácilmente tablas de puntos que satisfagan la ecuación dada.

Ejemplo$\PageIndex{4}$

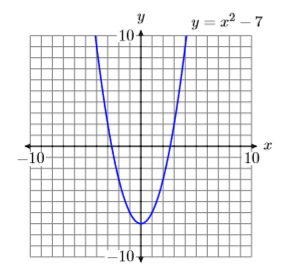
Utilice la calculadora gráfica para ayudar a crear una tabla de puntos que satisfaga la ecuación$y = x^2−7$. Traza los puntos en tu tabla. Si no sientes que hay suficiente evidencia para imaginar cuál será la forma final de la gráfica, usa la calculadora para agregar más puntos a tu tabla y trazarlos. Continúa este proceso hasta que estés convencido de la forma final de la gráfica.

Solución

higo 3.1.12.png — Figura$\PageIndex{12}$ : La calculadora gráfica.

El primer paso es cargar la ecuación$y = x^2−7$ i nal menú Y = de la calculadora gráfica. La fila superior de botones de tu calculadora (ver Figura$\PageIndex{12}$) tiene la siguiente apariencia:

fig 3.1.a.png — Figura$\PageIndex{13}$. Utilice las teclas de flecha arriba y abajo (ver Figura$\PageIndex{15}$) para mover el cursor después de Y1 = en el menú Y =, luego use las siguientes pulsaciones de teclas para ingresar a la ecuación$y = x^2 −7$. El resultado se muestra en la Figura$\PageIndex{14}$.

$fig 3.1.b.png$

higo 3.1.13.png — Figura$\PageIndex{13}$ : Abrir el menú Y =. Figura **$\PageIndex{14}$**: Ingresando a la ecuación$y = x^2 −7$.

alt — Figura$\PageIndex{13}$ : Abrir el menú Y =. Figura **$\PageIndex{14}$**: Ingresando a la ecuación$y = x^2 −7$.

higo 3.1.15.png — Figura$\PageIndex{15}$ : Las teclas de flecha mueven el cursor.

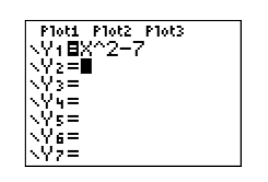
El siguiente paso es “configurar” la mesa. Primero, tenga en cuenta que la calculadora tiene impreso simbolismo en su caja encima de cada uno de sus botones. Encima del botón VENTANA notarás la frase TBLSET. Tenga en cuenta que está en el mismo color que el botón 2ND. Así, para abrir la ventana de configuración de la tabla, ingrese las siguientes pulsaciones de teclas.

Figura$\PageIndex{16}$) igual al primer valor x que desea ver en su tabla. En este caso, ingrese$−4$ después de TBLStart. SettBL al incremento que desee para sus$x$ -valores. En este caso, establecer Tbl igual a$1$. Finalmente, establezca tanto las variables independientes como las dependientes como “automáticas”. En cada caso, use las teclas de flecha para resaltar la palabra AUTO y presione ENTRAR. El resultado se muestra en la Figura$\PageIndex{16}$.

fig 3.1.c.png — Figura$\PageIndex{16}$) igual al primer valor x que desea ver en su tabla. En este caso, ingrese$−4$ después de TBLStart. SettBL al incremento que desee para sus$x$ -valores. En este caso, establecer Tbl igual a$1$. Finalmente, establezca tanto las variables independientes como las dependientes como “automáticas”. En cada caso, use las teclas de flecha para resaltar la palabra AUTO y presione ENTRAR. El resultado se muestra en la Figura$\PageIndex{16}$.

A continuación, anote que la palabra TABLE encima del botón GRAPADO está en el mismo color que la tecla 2ND. Para abrir el TABLE, ingrese las siguientes pulsaciones de teclas.

fig 3.1.d.png — Figura$\PageIndex{17}$. Tenga en cuenta que puede usar las teclas de flecha arriba y abajo para desplazarse por la tabla.

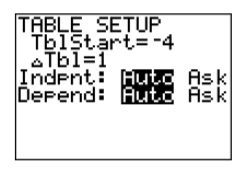
higo 3.1.16.png — Figura$\PageIndex{16}$ : Abrir el menú TBLSET. **Figura$\PageIndex{17}$** : Tabla de puntos satisfactorios$y = x^2 −7$.

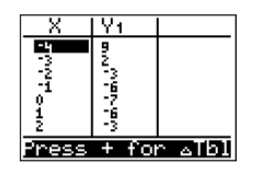
higo 3.1.17.png — Figura$\PageIndex{16}$ : Abrir el menú TBLSET. **Figura$\PageIndex{17}$** : Tabla de puntos satisfactorios$y = x^2 −7$.

A continuación, ingresa los resultados de la tabla de tu calculadora en una tabla en una hoja de papel cuadriculado, luego traza los puntos en la tabla. Los resultados se muestran en la Figura$\PageIndex{18}$.

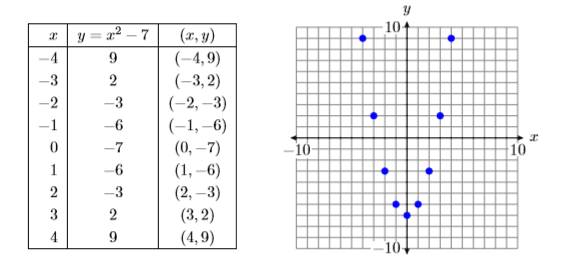
higo 3.1.18.png — Figura$\PageIndex{18}$ : Trazar nueve puntos que satisfacen la ecuación$y = x^2 −7$.

En Figura$\PageIndex{18}$, la forma eventual de la gráfica de$y = x^2 −7$ puede ser ya evidente, pero vamos a sumar algunos puntos más a nuestra tabla y trazarlos. Abra la ventana de “configuración” de la mesa nuevamente presionando 2ND VENTANA. Establezca TblStart en de$−4$ nuevo, luego establezca el incremento Tbl en$0.5$. El resultado se muestra en la Figura$\PageIndex{19}$.

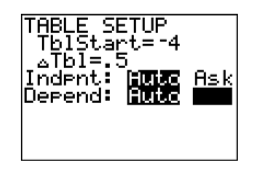
higo 3.1.19.png — Figura$\PageIndex{19}$ : SettBL igual a 0.5. **Figura$\PageIndex{20}$:** Más puntos satisfactorios$y = x^2 −7$.

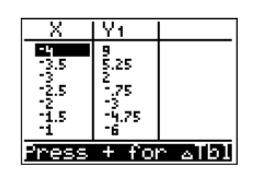
higo 3.1.20.png — Figura$\PageIndex{19}$ : SettBL igual a 0.5. **Figura$\PageIndex{20}$:** Más puntos satisfactorios$y = x^2 −7$.

Agrega estos nuevos puntos a la tabla en tu papel cuadriculado y grácalos (ver Figura$\PageIndex{21}$).

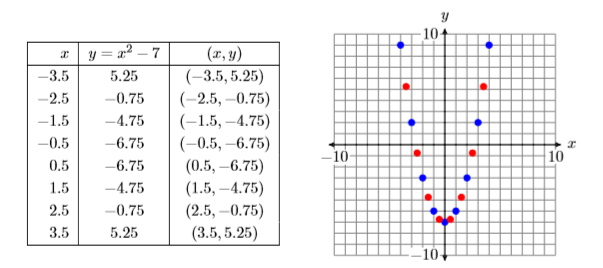
higo 3.1.21.png — Figura$\PageIndex{21}$ : Sumando puntos adicionales a la gráfica de$y = x^2 −7$.

Hay un número inﬁnito de puntos que satisfacen la ecuación$y = x^2−7$. En Figura$\PageIndex{21}$, hemos trazado solo$17$ puntos que satisfacen la ecuación$y = x^2 −7$. Sin embargo, la colección de puntos en la Figura$\PageIndex{21}$ sugiere que si tuviéramos que trazar el resto de los puntos que satisfacen la ecuación$y = x^2 −7$, el resultado sería la curva (llamada parábola) que se muestra en la Figura$\PageIndex{22}$.

higo 3.1.22.png — Figura$\PageIndex{22}$: La gráfica de$y = x^2 −7$ es una curva llamada parábola.