3.3: Tarifas y Pendiente

Última actualización
Guardar como PDF

Page ID: 111551

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Abramos esta sección con una aplicación del concepto de tasa.

Independiente versus dependiente

Es tradicional colocar la variable independiente en el eje horizontal y la variable dependiente en el eje vertical.

Ejemplo$\PageIndex{1}$

Un objeto se deja caer del reposo, luego comienza a recoger velocidad a una velocidad constante de$10$ metros por segundo cada segundo ($10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$o$10\mathrm{m} / \mathrm{s}^{2}$). Dibuje el gráfico de la velocidad del objeto versus tiempo.

Solución

En este ejemplo, la velocidad del objeto depende del tiempo. Esto hace que la velocidad sea la variable dependiente y el tiempo la variable independiente.

Siguiendo esta guía, colocamos el tiempo en el eje horizontal y la velocidad en el eje vertical. En Figura$\PageIndex{1}$, tenga en cuenta que hemos etiquetado cada eje con las variables dependientes e independientes ($v$y$t$), y hemos incluido las unidades ($\mathrm{m} / \mathrm{s}$y$\mathrm{s}$) en nuestras etiquetas. A continuación, necesitamos escalar cada eje. Al determinar una escala para cada eje, tenga en cuenta dos pensamientos:

Elija una escala que haga conveniente trazar los datos dados.
Elija una escala que permita que todos los datos dados se ajusten a la gráfica.

En este ejemplo, queremos una escala que haga conveniente mostrar que la velocidad está aumentando a una velocidad de$10$ metros por segundo ($10\mathrm{m} / \mathrm{s}$) cada segundo ($\mathrm{m} / \mathrm{s}$). Un enfoque posible es hacer que cada marca de verificación en el eje horizontal sea igual a$1 \mathrm{s}$ y cada marca en el eje vertical igual a$10\mathrm{m} / \mathrm{s}$.

higo 3.3.1.png — Figura$\PageIndex{1}$ : Etiquetar y escalar cada eje. Incluya unidades con etiquetas.

A continuación, en el momento$t=0 \mathrm{s}$, la velocidad es$v=0 \mathrm{m} / \mathrm{s}$. Este es el punto$(t, v)=(0,0)$ trazado en la Figura$\PageIndex{2}$. En segundo lugar, la velocidad a la que aumenta la velocidad es ($10\mathrm{m} / \mathrm{s}$) por segundo. Esto significa que cada vez que te mueves$1$ segundo a la derecha, la velocidad aumenta en ($10\mathrm{m} / \mathrm{s}$).

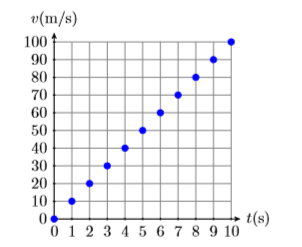
higo 3.3.2.png — Figura$\PageIndex{2}$ : Empezar en$(0,0)$, luego moverse continuamente hacia la$1$ derecha y$10$ hacia arriba.

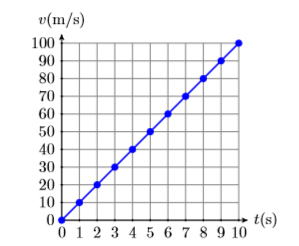
En Figura$\PageIndex{2}$, comience en$(0,0)$, luego mueva$1 \mathrm{s}$ hacia la derecha y ($10\mathrm{m} / \mathrm{s}$) hacia arriba. Esto te coloca en el punto$(1,10)$, que dice que después del$1$ segundo, la velocidad de la partícula es ($10\mathrm{m} / \mathrm{s}$). Continuar de esta manera, moviéndose continuamente$1 \mathrm{s}$ hacia la derecha y ($10\mathrm{m} / \mathrm{s}$) hacia arriba. Esto produce la secuencia de puntos que se muestra en la Figura$\PageIndex{2}$. Obsérvese que esta tasa constante de$10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$ fuerza la gráfica de la velocidad frente al tiempo a ser una línea, como se representa en la Figura$\PageIndex{3}$.

alt — Figura$\PageIndex{3}$ : La velocidad constante obliga a la gráfica a ser una línea.

higo 3.3.3.png — Figura$\PageIndex{3}$ : La velocidad constante obliga a la gráfica a ser una línea.

Ejercicio$\PageIndex{1}$

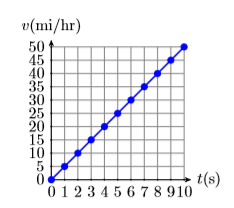
A partir del descanso, un automóvil cobra velocidad a una tasa constante de$5$ millas por hora cada segundo (5$(\mathrm{mi} / \mathrm{hr}) / \mathrm{s}$). Dibuje el gráfico de la velocidad del objeto versus tiempo.

Contestar: $Ejercicio 3.3.1.png$

Medición del Cambio en una Variable

Para calcular el cambio en alguna cantidad, tomamos una diferencia. Por ejemplo, supongamos que la temperatura en la mañana es$40^{\circ} \mathrm{F}$, luego por la tarde la temperatura mide$60^{\circ} \mathrm{F}$ (F significa temperatura Fahrenheit). Entonces el cambio de temperatura se encuentra tomando una diferencia.

\[\begin{aligned} \text { Change in temperature } &=\text { Afternoon temperature - Morning temperature } \\ &=60^{\circ} \mathrm{F}-40^{\circ} \mathrm{F} \\ &=20^{\circ} \mathrm{F} \end{aligned} \nonumber\]

Por lo tanto, hubo un incremento de veinte grados en la temperatura de la mañana a la tarde.

Ahora, supongamos que la temperatura vespertina mide$50^{\circ} \mathrm{F}$. Para calcular el cambio de temperatura de la tarde a la noche, nuevamente restamos.

\[\begin{aligned} \text { Change in temperature } &=\text { Evening temperature - Afternoon temperature } \\ &=50^{\circ} \mathrm{F}-60^{\circ} \mathrm{F} \\ &=-10^{\circ} \mathrm{F} \end{aligned} \nonumber \]

Hubo una disminución de diez grados en la temperatura de la tarde a la noche.

Cálculo del Cambio en una Cantidad

Para calcular el cambio en una cantidad, reste la medición anterior de la medición posterior.

Dejar$T$ representar la temperatura. A los matemáticos les gusta usar el simbolismo$\Delta T$ para representar el cambio de temperatura. Para el cambio de temperatura de la mañana a la tarde, escribiríamos$\Delta T=20^{\circ} \mathrm{F}$. Para el cambio de tarde a noche, escribiríamos$\Delta T=-10^{\circ} \mathrm{F}$.

Matemáticos y científicos hacen uso frecuente del alfabeto griego, cuyas primeras letras son:

$\begin{array}{ll}{\alpha, \beta, \gamma, \delta, \ldots} & {\text { (Greek alphabet, lower case) }} \\ {A, B, \Gamma, \Delta, \ldots} & {\text { (Greek alphabet, upper case) }} \\ {a, b, c, d, \ldots} & {\text { (English alphabet) }}\end{array}$

Así, la letra griega$\Delta T$, la forma mayúscula de$\delta$, se correlaciona con la letra 'd' en el alfabeto inglés. ¿Por qué los matemáticos hicieron esta elección de letra para representar el cambio en una cantidad? Porque para encontrar el cambio en una cantidad, tomamos una diferencia, y la palabra “diferencia” comienza con la letra 'd'. Así, también$\Delta T$ se pronuncia “la diferencia en T.”

Pronunciaciones Importantes

Dos formas de pronunciar el simbolismo ΔT.

$\Delta T$se pronuncia “el cambio en T.”
$\Delta T$también se pronuncia “la diferencia en T.”

Pendiente como tasa

Aquí está la definición de la pendiente de una línea.

Talud

La pendiente de una línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente. Por ejemplo, si la variable dependiente es$y$ y la variable independiente es$x$, entonces la pendiente de la línea es:

Talud$=\dfrac{\Delta y}{\Delta x}$

Ejemplo$\PageIndex{2}$

En Ejemplo$\PageIndex{1}$, un objeto liberado del reposo vio que su velocidad aumentaba a una velocidad constante de$10$ metros por segundo por segundo ($10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$o$10\mathrm{m} / \mathrm{s}^{2}$). Esta tasa constante obligó a la gráfica de la velocidad frente al tiempo a ser una línea, mostrada en la Figura$\PageIndex{3}$. Calcular la pendiente de esta línea.

Solución

Comience seleccionando dos puntos$P(2,20)$ y$Q(8,80)$ en la línea, como se muestra en la Figura$\PageIndex{4}$. Para encontrar la pendiente de esta línea, la definición requiere que encontremos la velocidad a la que la variable dependiente$v$ cambia con respecto a la variable independiente$t$. Es decir, la pendiente es el cambio en$v$ dividido por el cambio en$t$. En símbolos:

Talud$=\dfrac{\Delta v}{\Delta t}$

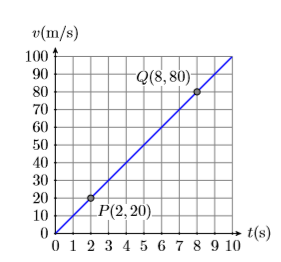
higo 3.3.4.png — Figura$\PageIndex{4}$: Escoge dos puntos para calcular la pendiente.

Ahora, a medida que avanzamos de punto$P(2,20)$ a punto$Q(8,80)$, la velocidad cambia de$20\mathrm{m} / \mathrm{s}$ a$80\mathrm{m} / \mathrm{s}$. Así, el cambio en la velocidad es:

$\begin{aligned} \Delta v &=80 \mathrm{m} / \mathrm{s}-20 \mathrm{m} / \mathrm{s} \\ &=60 \mathrm{m} / \mathrm{s} \end{aligned}$

De igual manera, a medida que nos movemos del punto P (2,20) al punto Q (8,80), el tiempo cambia de 2 segundos a 8 segundos. Así, el cambio en el tiempo es:

$\begin{aligned} \Delta t &=8 \mathrm{s}-2 \mathrm{s} \\ &=6 \mathrm{s} \end{aligned}$

Ahora que tenemos tanto el cambio en las variables dependientes como independientes, podemos calcular la pendiente.

$\begin{aligned} \text { Slope } &=\frac{\Delta v}{\Delta t} \\ &=\frac{60 \mathrm{m} / \mathrm{s}}{6 \mathrm{s}} \\ &=10 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{s}} \end{aligned}$

Por lo tanto, la pendiente de la línea es de$10$ metros por segundo por segundo ($10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$o$10\mathrm{m} / \mathrm{s}^{2}$).

La pendiente de una línea no depende de los puntos que seleccione. Intentemos de nuevo el cálculo de pendiente, utilizando dos puntos diferentes y una presentación más compacta de los cálculos requeridos. Puntos de selección$P(3,30)$ y$Q(7,70)$ como se muestra en la Figura$\PageIndex{5}$. Usando estos dos nuevos puntos, la pendiente es la velocidad a la que la variable dependiente$v$ cambia con respecto a la variable independiente$t$.

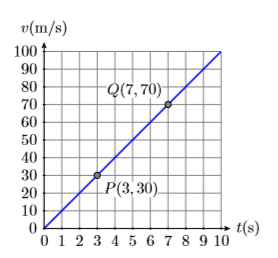
higo 3.3.5.png — Figura$\PageIndex{5}$ : La pendiente no depende de los puntos que seleccionemos en la línea.

$\begin{aligned} \text { Slope } &=\frac{\Delta v}{\Delta t} \\ &=\frac{70 \mathrm{m} / \mathrm{s}-30 \mathrm{m} / \mathrm{s}}{7 \mathrm{s}-3 \mathrm{s}} \\ &=\frac{40 \mathrm{m} / \mathrm{s}}{4 \mathrm{s}} \\ &=10 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{s}} \end{aligned}$

Nuevamente, la pendiente de la línea es$10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$.

Ejercicio$\PageIndex{2}$

A partir del descanso, un automóvil cobra velocidad a una velocidad constante de 5 millas por hora cada segundo (5 (mi/hr) /s). La velocidad constante obliga a que el gráfico de la velocidad del objeto versus el tiempo sea una línea. Calcular la pendiente de esta línea.

Contestar: $5(\mathrm{mi} / \mathrm{hr}) / \mathrm{s}$

Ejemplo$\PageIndex{2}$ señala el siguiente hecho.

La pendiente es independiente de los puntos seleccionados

No importa qué dos puntos escojas en la línea para calcular su pendiente.

El siguiente ejemplo demuestra que la pendiente también es independiente del orden de resta.

Ejemplo$\PageIndex{3}$

Calcular la pendiente de la línea que pasa por los puntos$P(−1,−2)$ y$Q(3,3)$.

Solución

Primero, dibuje la línea que pasa por los puntos P (−1, −2) y Q (3,3) (ver Figura$\PageIndex{6}$).

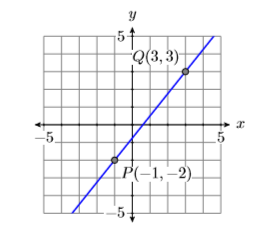
higo 3.3.6.png — Figura$\PageIndex{6}$ : Calcular la pendiente de la línea que pasa por los puntos$P(−1,−2)$ y$Q(3,3)$.

Para calcular la pendiente de la línea a través de los puntos$P(−1,−2)$ y$Q(3,3)$, debemos calcular el cambio tanto en las variables independientes como dependientes. Esto lo haremos de dos maneras distintas.

¡Advertencia!

Si no eres consistente en la dirección que restas, no obtendrás la respuesta correcta para la pendiente.

Por ejemplo:\[\dfrac{3-(-2)}{-1-3}=-\dfrac{5}{4} \nonumber \]

En este caso, restamos la$y$ coordenada -del punto$P(−1,−2)$ de la$y$ coordenada -del punto$Q(3,3)$, pero luego cambiamos caballos en midstream, restando la$x$ coordenada -del punto$Q(3,3)$ de la$x$ coordenada -del punto$P(−1,−2)$. Tenga en cuenta que obtenemos el negativo de la respuesta correcta.

Método 1

Restar las coordenadas del punto$P(−1,−2)$ de las coordenadas del punto$Q(3,3)$.

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-(-2)}{3-(-1)} \\ &=\dfrac{5}{4} \end{aligned} \nonumber \]

Método 2

Restar las coordenadas del punto$Q(3,3)$ de las coordenadas del punto$P(−1,−2)$.

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-2-3}{-1-3} \\ &=\dfrac{-5}{-4} \\ &=\dfrac{5}{4} \end{aligned} \nonumber \]

Tenga en cuenta que independientemente de la dirección de resta, la pendiente es$5/4$.

Ejercicio$\PageIndex{3}$

Calcular la pendiente de la línea que pasa por los puntos P (−3,1) y Q (2,4).

Contestar: $3/5$

Ejemplo$\PageIndex{3}$ demuestra el siguiente hecho.

La dirección de la resta no importa

Al calcular la pendiente de una línea a través de dos puntos$P$ y$Q$, no importa de qué manera restes, siempre que permanezcas consistente en tu elección de dirección.

La pendiente de una línea

Necesitamos examinar si nuestra definición de pendiente coincide con ciertas expectativas.

Pendiente e inclinación de una línea

La pendiente de una línea es un número que nos indica cuán empinada es la línea.

Si la pendiente es un número que mide la inclinación de una línea, entonces uno esperaría que una línea más pronunciada tuviera una pendiente mayor.

Ejemplo$\PageIndex{4}$

Grafica dos líneas, la primera pasando por los puntos$P(−3,−2)$ $Q(3,2)$ y la segunda por los puntos$R(−1,−3)$ y$S(1,3)$. Calcular la pendiente de cada línea y comparar los resultados.

Solución

Se muestran las gráficas de las dos líneas a través de los puntos dados, la primera en la Figura$\PageIndex{7}$ y la segunda en la Figura$\PageIndex{8}$. Tenga en cuenta que la línea en la Figura$\PageIndex{7}$ es menos empinada que la línea de la Figura$\PageIndex{8}$.

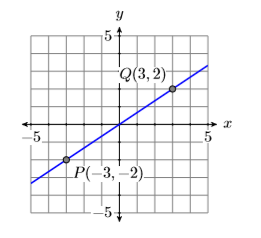
higo 3.3.7.png — Figura$\PageIndex{7}$: Esta línea es menos empinada que la línea de la derecha. **Figura$\PageIndex{8}$:** Esta línea es más pronunciada que la línea de la izquierda.

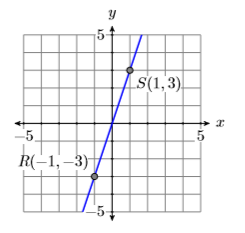
higo 3.3.8.png — Figura$\PageIndex{7}$: Esta línea es menos empinada que la línea de la derecha. **Figura$\PageIndex{8}$:** Esta línea es más pronunciada que la línea de la izquierda.

Recuerde, la pendiente de la línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente. Tanto en Figura$\PageIndex{7}$ como en Figura$\PageIndex{8}$, la variable dependiente es$y$ y la variable independiente es$x$.

Restar las coordenadas del punto$P(−3,−2)$ de las coordenadas del punto$Q(3,2)$.

\[\begin{aligned} \text { Slope of first line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{2-(-2)}{3-(-3)} \\ &=\dfrac{4}{6} \\ &=\dfrac{2}{3} \end{aligned} \nonumber \]

Restar las coordenadas del punto$R(−1,−3)$ del punto$S(1,3)$.

\[\begin{aligned} \text { Slope of second line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-(-3)}{1-(-1)} \\ &=\dfrac{6}{2} \\ &=3 \end{aligned} \nonumber \]

Tenga en cuenta que ambas líneas van cuesta arriba y ambas tienen pendientes positivas. También, tenga en cuenta que la pendiente de la segunda línea es mayor que la pendiente de la primera línea. Esto es consistente con el hecho de que la segunda línea es más pronunciada que la primera.

Ejercicio$\PageIndex{4}$

Calcular la pendiente de la línea que pasa por los puntos$P(−2,−3)$ and $Q(2,5)$. Then compute the slope of the line passing through the points $R(−2,−1)$ and $S(5,3)$, and compare the two slopes. Which line is steeper?

Contestar: La primera línea tiene pendiente$2$, y la segunda línea tiene pendiente$4/7$. La primera línea es más pronunciada.

En Ejemplo$\PageIndex{4}$, ambas líneas se inclinaron cuesta arriba y ambas tuvieron pendientes positivas, teniendo la pendiente más pronunciada de las dos líneas la mayor pendiente. Veamos ahora dos líneas que se inclinan cuesta abajo.

Ejemplo$\PageIndex{5}$

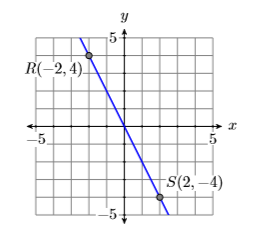
Grafica dos líneas, la primera pasando por los puntos$P(−3,1)$$Q(3,−1)$ y la segunda por los puntos$R(−2,4)$ y$S(2,−4)$. Calcular la pendiente de cada línea y comparar los resultados.

Solución

Se muestran las gráficas de las dos líneas a través de los puntos dados, la primera en la Figura$\PageIndex{9}$ y la segunda en la Figura$\PageIndex{10}$. Tenga en cuenta que la línea en la Figura$\PageIndex{9}$ va cuesta abajo menos rápido que la línea de la Figura$\PageIndex{10}$. Recuerde, la pendiente de la línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente. Tanto en Figura$\PageIndex{9}$ como en Figura$\PageIndex{10}$, la variable dependiente es$y$ y la variable independiente es$x$.

higo 3.3.9.png — Figura$\PageIndex{9}$: Esta línea va cuesta abajo más despacio que la línea de la derecha.

fig3.3.10.png — Figura$\PageIndex{10}$: Esta línea va cuesta abajo más rápido que la línea de la izquierda.

Restar las coordenadas del punto$P(−3,1)$ de las coordenadas del punto$Q(3,−1)$.

\[\begin{aligned} \text { Slope of first line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-1-1}{3-(-3)} \\ &=\dfrac{-2}{6} \\ &=-\dfrac{1}{3} \end{aligned} \nonumber \]

Restar las coordenadas del punto$R(−2,4)$ de las coordenadas del punto$S(2,−4)$.

\[\begin{aligned} \text { Slope of second line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-4-4}{2-(-2)} \\ &=\dfrac{-8}{4} \\ &=-2 \end{aligned} \nonumber \]

Tenga en cuenta que ambas líneas van cuesta abajo y ambas tienen pendientes negativas. También, tenga en cuenta que la magnitud (valor absoluto) de la pendiente de la segunda línea es mayor que la magnitud de la pendiente de la primera línea. Esto es consistente con el hecho de que la segunda línea se mueve cuesta abajo más rápidamente que la primera.

Ejercicio$\PageIndex{5}$

Calcular la pendiente de la línea que pasa por los puntos$P(−3,3)$ and $Q(3,−5)$. Then compute the slope of the line passing through the points $R(−4,1)$ and $S(4,−3)$, and compare the two slopes. Which line is steeper?

Contestar: La primera línea tiene pendiente$−4/3$, y la segunda línea tiene pendiente$−1/2$. La primera línea es más pronunciada.

¿Y las pendientes de las líneas verticales y horizontales?

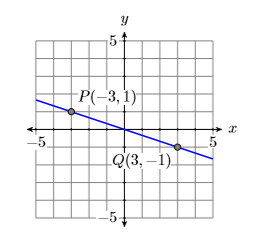
Ejemplo$\PageIndex{6}$

Calcular las pendientes de las líneas verticales y horizontales que pasan por el punto$(2,3)$.

Solución

Primero dibuja un boceto de las líneas verticales y horizontales que pasan por el punto (2,3). A continuación, seleccione un segundo punto en cada línea como se muestra en las Figuras$\PageIndex{11}$ y$\PageIndex{12}$.

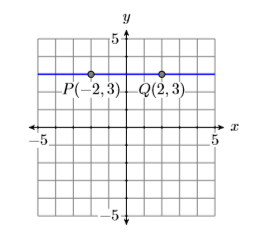
higo 3.3.11.png — Figura$\PageIndex{11}$: Una línea horizontal a través$(2,3)$.

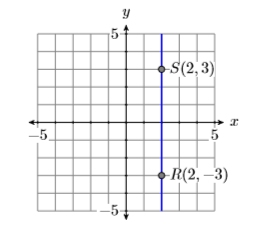
higo 3.3.12.png — Figura$\PageIndex{12}$: Una línea vertical a través$(2,3)$.

Las pendientes de las líneas horizontales y verticales se calculan de la siguiente manera.

Restar las coordenadas del punto$P(−2,3)$ de las coordenadas del punto$Q(2,3)$.

\[\begin{aligned} \text { Slope of horizontal line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-3}{2-(-2)} \\ &=\dfrac{0}{4} \\ &=0 \end{aligned} \nonumber \]

Así, la pendiente de la línea horizontal es cero, lo cual tiene sentido porque una línea horizontal no va ni cuesta arriba ni cuesta abajo.

Restar las coordenadas del punto$(2,−3)$ de las coordenadas del punto$S(2,3)$.

\[\begin{aligned} \text { Slope of vertical line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-(-3)}{2-2} \\ &=\dfrac{6}{0} \\ &=\text { undefined } \end{aligned} \nonumber \]

La división por cero no está definida. De ahí que la pendiente de una línea vertical sea indefinida. Nuevamente, esto tiene sentido porque a medida que las líneas cuesta arriba se vuelven cada vez más pronunciadas, sus pendientes aumentan sin ataduras.

Ejercicio$\PageIndex{6}$

Calcular las pendientes de las líneas verticales y horizontales que pasan por h el punto$(−4,1)$.

Contestar: La pendiente de la línea vertical es indefinida. La pendiente de la segunda línea es$0$.

La geometría de la pendiente de una línea

Comenzamos nuestra discusión geométrica de la pendiente de una línea con un ejemplo, calculando la pendiente de una línea que pasa por los puntos$P(2,3)$ y$Q(8,8)$. Antes de comenzar primero calcularemos el cambio en$y$ y el cambio en$x$ restando las coordenadas del punto$P(2,3)$ de las coordenadas del punto$Q(8,8)$.

\[\begin{aligned} \mathrm{Slope} &=\dfrac{\Delta y}{\dfrac{\Delta x}{\Delta x}} \\ &=\dfrac{8-3}{8-2} \\ &=\dfrac{5}{6} \end{aligned} \nonumber \]

Así, la pendiente de la línea a través de los puntos$P(2,3)$ y$Q(8,8)$ es$5/6$.

Para utilizar un enfoque geométrico para encontrar la pendiente de la línea, primero dibuja la línea a través de los puntos$P(2,3)$ y$Q(8,8)$ (ver Figura$\PageIndex{13}$). A continuación, dibuja un triángulo rectángulo con lados paralelos a los ejes horizontal y vertical, usando los puntos$P(2,3)$ y$Q(8,8)$ como vértices. A medida que se mueve de punto$P$ a punto$R$ en la Figura$\PageIndex{13}$, tenga en cuenta que el cambio en$x$ es$\Delta x=6$ (cuente las marcas de verificación ¹).

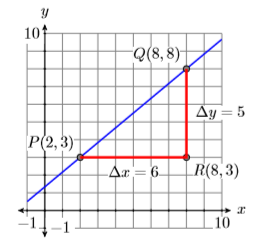
higo 3.3.13.png — Figura$\PageIndex{13}$: Determinar la pendiente de la línea a partir de la gráfica.

A medida que luego se mueve de punto$R$ a punto$Q$, el cambio en$y$ es$\Delta y=5$ (cuente las marcas de verificación). Así, la pendiente es$\Delta y / \Delta x=5 / 6$, precisamente lo que obtuvimos en el cómputo anterior.

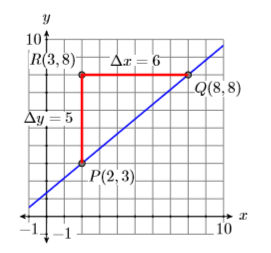
higo 3.3.14.png — Figura$\PageIndex{14}$: Determinar la pendiente de la línea a partir de la gráfica.

Por el contrario, en Figura$\PageIndex{14}$, comenzamos en el punto$P(2,3)$, luego movimos$5$ unidades ascendentes y unidades$6$ derechas. No obstante, el cambio en$y$ sigue siendo$\Delta y=5$ y el cambio en$x$ sigue siendo a$\Delta x=6$ medida que avanzamos de punto$P(2,3)$ a punto$Q(8,8)$. De ahí que la pendiente esté quieta$\Delta y / \Delta x=5 / 6$.

Subida sobre atropello

En la Figura e$\PageIndex{14}$, partimos en el punto$P(2,3)$, luego “subimos”$5$ unidades, luego “corremos”$6$ unidades a la derecha. Por esta razón, a algunos les gusta pensar en la pendiente como “subir sobre carrera”.

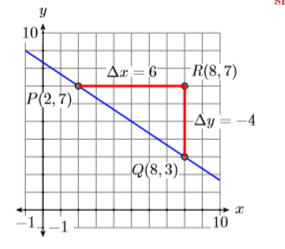
Consideremos un segundo ejemplo que se muestra en la Figura$\PageIndex{15}$. Tenga en cuenta que la línea se inclinó cuesta abajo, por lo que esperamos que la pendiente sea un número negativo.

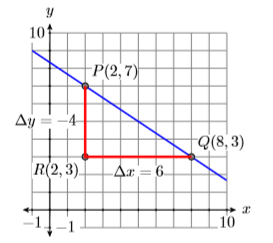
higo 3.3.15.png — Figura$\PageIndex{15}$: Determinar la pendiente de la línea a partir de la gráfica.

En Figura$\PageIndex{15}$, hemos dibujado un triángulo rectángulo con lados paralelos a los ejes horizontal y vertical, usando los puntos$P(2,7)$ y$Q(8,3)$ como vértices. A medida que se mueve de punto$P$ a punto$R$ en Figura$\PageIndex{15}$, el cambio en$y$ es$\Delta y=-4$ (cuente las marcas de verificación y tenga en cuenta que sus valores de y van disminuyendo a medida que avanza de$P$ a$R$). A medida que se mueve de punto$R$ a punto$Q$, el cambio es$x$ es$\Delta x=6$ (cuente las marcas de verificación y tenga en cuenta que sus valores de$x$ van aumentando a medida que avanza de$R$ a$Q$). En este caso, la “subida” es negativa, mientras que la “corrida” es positiva.

Así, la pendiente es$\Delta y / \Delta x=-4 / 6$, o$−2/3$. Tenga en cuenta que la pendiente es negativa, como se anticipó.

higo 3.3.16.png — Figura$\PageIndex{16}$: Determinar la pendiente de la línea a partir de la gráfica.

En Figura$\PageIndex{16}$, hemos dibujado nuestro triángulo en el lado opuesto de la línea. En este caso, a medida que te mueves de punto$P$ a punto$R$ en la Figura$\PageIndex{16}$, el cambio en$x$ es$\Delta x=6$ (cuente las marcas de verificación y tenga en cuenta que sus valores de$x$ van aumentando a medida que avanza de$P$ a$R$). A medida que se mueve de punto$R$ a punto$Q$, el cambio es$y$ es$\Delta y=-4$ (cuente las marcas de verificación y tenga en cuenta que sus valores de$y$ van disminuyendo a medida que avanza de$R$ a$Q$). Así, la pendiente sigue siendo$\Delta y / \Delta x=-4 / 6$, o$−2/3$.

Podemos verificar nuestros cálculos geométricos de la pendiente restando las coordenadas del punto del punto$P(2,7)$ del punto$Q(8,3)$.
\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-7}{8-2} \\ &=\dfrac{-4}{6} \\ &=-\dfrac{2}{3} \end{aligned} \nonumber \]

Esto concuerda con los cálculos realizados en Figuras$\PageIndex{15}$ y$\PageIndex{16}$.

Veamos un último ejemplo.

Ejemplo$\PageIndex{7}$

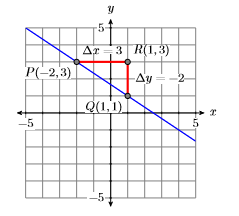
Dibuje la línea que pasa por el punto$(−2,3)$ con pendiente$−2/3$.

Solución

La pendiente es$−2/3$, por lo que la línea debe ir cuesta abajo. En Figura$\PageIndex{17}$, comenzamos en el punto$P(−2,3)$, movemos$3$ las unidades de la derecha al punto$R(1,3)$, luego bajamos$2$ las unidades al punto$Q(1,1)$. Dibuja la línea a través de los puntos$P$$Q$ y ya estás listo.

higo 3.3.17.png — Figura$\PageIndex{17}$: Comience en$P(−2,3)$, luego mueva hacia la derecha$3$ y hacia abajo$2$. La línea resultante tiene pendiente$−2/3$.

En Figura$\PageIndex{18}$, tomamos un enfoque diferente que da como resultado la misma línea. Comience en el punto$P(−2,3)$, mueva$4$ las unidades hacia abajo hacia el punto$R(−2,−1)$, luego$6$ las unidades derechas al punto$Q(4,−1)$. Dibuja una línea a través de los puntos$P$$Q$ y ya estás listo.

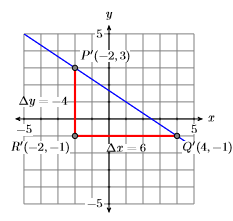
higo 3.3.18.png — Figura$\PageIndex{18}$: Comenzando en$P(−2,3)$ y moviéndose hacia abajo$4$ y hacia la derecha$6$ también arroja una pendiente de$−2/3$.

El triángulo$PQR$ en la Figura$\PageIndex{17}$ es similar al triángulo$PQR$ de la Figura$\PageIndex{18}$, por lo que sus lados son proporcionales. En consecuencia, la pendiente de la línea a través de puntos$P(−2,3)$ y$Q(4,−1)$,

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-4}{6} \\ &=-\dfrac{2}{3} \end{aligned} \nonumber \]

reduce a la pendiente de la línea a través de los puntos$P$ y$Q$ en la Figura$\PageIndex{17}$.

Ejercicio$\PageIndex{7}$

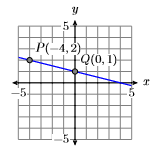
Croquis de la línea que pasa por el punto$(−4,2)$ with slope $−1/4$.

Contestar: $Ejercicio 3.3.7.png$

Un resumen de hechos sobre la pendiente de una línea

Presentamos un resumen de los hechos aprendidos en esta sección.

La pendiente de una línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente. Si$y$ es la variable dependiente y$x$ es la variable independiente, entonces la pendiente es\[\text {Slope}=\dfrac{\Delta y}{\Delta x} \nonumber \] donde$\Delta y$ está el cambio en$y$ (diferencia en$y$) y$\Delta x$ es el cambio en$x$ (diferencia en$x$).
Si una línea tiene pendiente positiva, entonces la línea se inclinará cuesta arriba mientras “barres los ojos de izquierda a derecha”. Si dos líneas tienen pendiente positiva, entonces la línea con la pendiente más grande se eleva más rápidamente.
Si una línea tiene pendiente negativa, entonces la línea se inclinará cuesta abajo mientras “barres los ojos de izquierda a derecha”. Si dos líneas tienen pendiente negativa, entonces la línea que tiene la pendiente con la magnitud mayor cae más rápidamente.
Las líneas horizontales tienen pendiente cero.
Las líneas verticales tienen pendiente indefinida.

Referencias

¹ Al contar las marcas de verificación, asegúrese de conocer la cantidad que representa cada marca de verificación. Por ejemplo, si cada marca de verificación representa dos unidades, y cuenta seis marcas de verificación al evaluar el cambio en$x$, entonces$\Delta x=12$.