3.4: Forma de pendiente-interceptación de una línea

Última actualización
Guardar como PDF

Page ID: 111552

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comenzamos con la definición de la$y$ -intercepción de una línea.

El$y$-intercept

El punto$(0,b)$ donde la gráfica de una línea cruza el$y$ eje -se llama la$y$ -intercepción de la línea.

Ahora vamos a generar la fórmula pendiente-intercepción para una línea que tiene$y$ -intercept$(0,b)$ y$\text {Slope} = m$ (ver Figura$\PageIndex{1}$). Déjese$(x,y)$ ser un punto arbitrario en la línea.

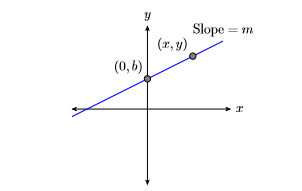
higo 3.4.1.png — Figura$\PageIndex{1}$: Línea con$y$ -intercepción en$(0,b)$ y$\text {Slope} = m$.

Comience con el hecho de que la pendiente de la línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente.

\[\text {Slope} =\dfrac{\Delta y}{\Delta x} \qquad \color{Red} \text {Slope formula.} \nonumber \]

Sustituto$m$ de la pendiente. Para determinar tanto el cambio en$y$ como el cambio en$x$, restar las coordenadas del punto$(0,b)$ del punto del punto$(x,y)$.

\[\begin{aligned} m&=\frac{y-b}{x-0} \quad \color {Red} \text { Substitute } m \text { for the Slope. } \Delta y =y-b \quad \color {Red} \text { and } \Delta x=x-0 .\\ m&=\frac{y-b}{x} \quad \color {Red}\text { Simplify. } \end{aligned} \nonumber \]

Borrar fracciones de la ecuación multiplicando ambos lados por el denominador común.

\[\begin{aligned} mx &= \left[\dfrac{y-b}{x}\right] x \quad \color {Red} \text { Multiply both sides by } x \\ mx &= y-b \quad \color {Red} \text { Cancel. } \end{aligned} \nonumber \]

Resolver para$y$.

\[\begin{aligned} mx+b&= y-b+b \quad \color {Red} \text { Add } b \text { to both sides. } \\ mx+b&= y \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Así, la ecuación de la línea es$y = mx + b$.

La forma Slope-Intercept de una línea

La ecuación de la línea que tiene$y$ intercepción$(0,b)$ y pendiente$m$ es:\[y = mx + b \nonumber \] Debido a que esta forma de una línea depende de conocer la pendiente$m$ y la intercepción$(0,b)$, esta forma se denomina la forma pendiente-intercepción de una línea.

Ejemplo$\PageIndex{1}$

Dibuje la gráfica de la línea que tiene ecuación$y=\dfrac{3}{5} x+1$.

Solución

Compare la ecuación$y=\dfrac{3}{5} x+1$ con la forma pendiente-intercepción$y = mx + b$, y tenga en cuenta que$m =3 /5$ y$b = 1$. Esto significa que la pendiente es$3/5$ y la$y$ -intercepción es$(0,1)$. Comience trazando la$y$ -intercepción$(0,1)$, luego mueva$3$ las unidades hacia arriba y las$5$ unidades de la derecha, llegando al punto$(5,4)$. Dibuja la línea a través de los puntos$(0,1)$ y$(5,4)$, luego etiquétalo con su ecuación$y=\dfrac{3}{5} x+1$.

higo 3.4.2.png — Figura$\PageIndex{2}$: Gráfica dibujada a mano de$y=\dfrac{3}{5} x+1$.

higo 3.4.3.png — Figura$\PageIndex{3}$: Seleccione **5:ZSquare** en el menú ZOOM para dibujar la gráfica de$y=\dfrac{3}{5} x+1$.

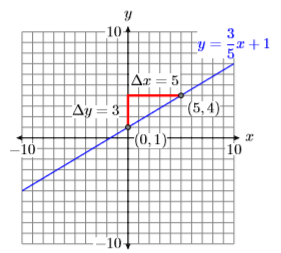
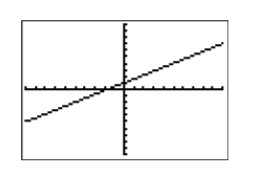
Cuando comparamos la imagen de la calculadora en Figura$\PageIndex{3}$ con la gráfica dibujada a mano en Figura$\PageIndex{2}$, obtenemos una mejor coincidencia.

Ejercicio$\PageIndex{1}$

Dibuje la gráfica de la línea que tiene ecuación$y=-\dfrac{4}{3} x-2$.

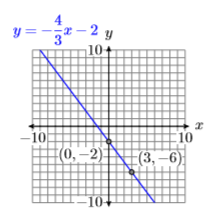
Contestar: $Ejercicio 3.4.1.png$

Ejemplo$\PageIndex{2}$

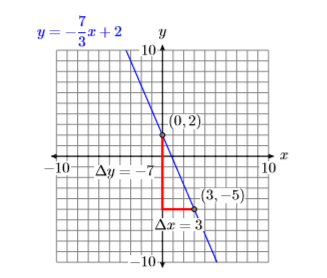
Dibuje la línea con$y$ -intercepción$(0,2)$ y pendiente$−7/3$. Etiquete la línea con la forma pendiente-intercepción de su ecuación.

Solución

Trazar la$y$ -intercepción$(0,2)$. Ahora usa la pendiente$−7/3$. Empezar en$(0,2)$, luego bajar siete unidades, seguido de un movimiento de tres unidades a la derecha al punto$(3,−5)$. Dibuja la línea a través de los puntos$(0,2)$ y$(3,−5)$. (Ver Figura$\PageIndex{4}$).

A continuación, la$y$ -intercepción es$(0,2)$, entonces$b = 2$. Además, la pendiente es$−7/3$, entonces$m = −7/3$. Sustituya estos números por la forma pendiente-intercepción de la línea.

\[\begin{aligned} y&= mx+b \quad \color {Red} \text { Slope-intercept form. } \\ y&= -\dfrac{7}{3} x+2 \quad \color {Red} \text { Substitute: }-7 / 3 \text { for } m, 2 \text { for } b . \end{aligned} \nonumber \]

Por lo tanto, la forma pendiente-intercepción de la línea es$y=-\dfrac{7}{3} x+2$. Etiquete la línea con esta ecuación.

higo 3.4.4.png — Figura$\PageIndex{4}$: Gráfica dibujada a mano de$y=-\dfrac{7}{3} x+2$

Comprobar: Para graficar$y=-\dfrac{7}{3} x+2$, ingresa$-7 / 3 * X+2$ Y1 en el menú Y =. Seleccione 6:ZStandard en el menú ZOOM, seguido de 5:ZSquare en el menú ZOOM para producir la gráfica que se muestra en la Figura$\PageIndex{6}$.

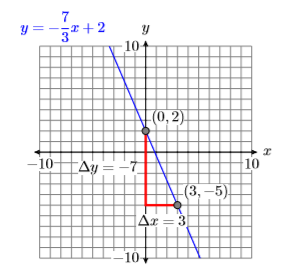
higo 3.4.5.png — Figura$\PageIndex{5}$: Gráfica dibujada a mano de$y=-\dfrac{7}{3} x+2$

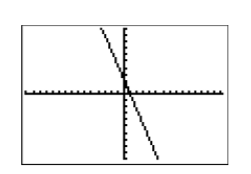
higo 3.4.6.png — Figura$\PageIndex{6}$: Seleccione **6:ZStandard** en el menú ZOOM, seguido de **5:ZSquare** en el menú ZOOM para producir la gráfica de la ecuación$y=-\dfrac{7}{3} x+2$

Esto proporciona una buena coincidencia del gráfico dibujado a mano en Figura$\PageIndex{5}$ y nuestro resultado de calculadora gráfica en Figura$\PageIndex{6}$.

Ejercicio$\PageIndex{2}$

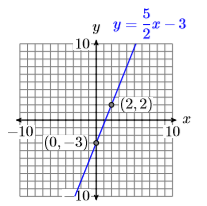
Dibuja la línea con$y$-intercept $(0,−3)$ and slope $5/2$. Label the line with the slope-intercept form of its equation.

Contestar: $Ejercicio 3.4.2.png$

Ejemplo$\PageIndex{3}$

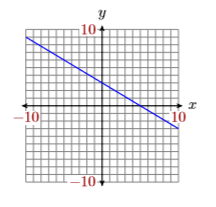
Utilice la gráfica de la línea en la siguiente figura para encontrar la ecuación de la línea.

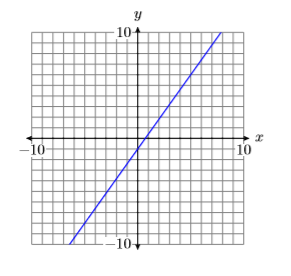
$Ejemplo 3.4.3.png$

Solución

Tenga en cuenta que el$y$-intercept of the line is $(0,−1)$ (See Figure $\PageIndex{7}$). Next, we try to locate a point on the line that passes directly through a lattice point, a point where a vertical and horizontal grid line intersect. In Figure $\PageIndex{7}$, we chose the point $(5,6)$. Now, starting at the $y$-intercept $(0,1)$, we move up $7$ units, then to the right $5$ units. Hence, the slope is $m=\Delta y / \Delta x$, or $m =7 /5$.

Note

We could also subtract the coordinates of point $(0,−1)$ from the coordinates of point $(5,6)$ to determine the slope. \[\dfrac{6-(-1)}{5-0}=\dfrac{7}{5} \nonumber \]

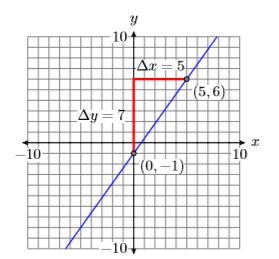
fig 3.4.7.png — Figure $\PageIndex{7}$: The line has $y$-intercept $(0,−1)$ and slope $7/5$.

Next, state the slope-intercept form, the substitute $7/5$ for $m$ and $−1$ for $b$.

\[\begin{aligned} y&= mx+b \quad \color {Red} \text { Slope-intercept form. } \\ y&= \dfrac{7}{5} x+(-1) \quad \color {Red} \text { Substitute: } 7 / 5 \text { for } m,-1 \text { for } b \end{aligned} \nonumber \]

Thus, the equation of the line is $y=\dfrac{7}{5} x-1$.

Check: This is an excellent situation to run a check on your graphing calculator.

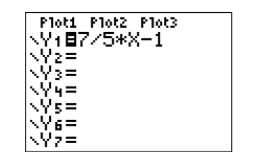
fig 3.4.8.png — Figure $\PageIndex{8}$: Enter $y=\dfrac{7}{5} x-1$ in the Y= menu.

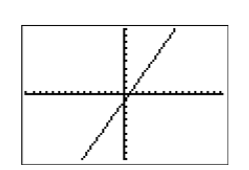
fig 3.4.9.png — Figure $\PageIndex{9}$: Select **6:ZStandard** followed by **5:ZSquare** (both from the ZOOM menu) to produce this graph.

When we compare the result in Figure $\PageIndex{9}$ with the original hand-drawn graph (see Figure $\PageIndex{7}$), we’re confident we have a good match.

Exercise $\PageIndex{3}$

Use the graph of the line in the figure below to find the equation of the line.

$Exercise 3.4.3.png$

Answer: $y=-\dfrac{3}{5} x+3$

Applications

Let’s look at a linear application.

Example $\PageIndex{4}$

Jason spots his brother Tim talking with friends at the library, located $300$ feet away. He begins walking towards his brother at a constant rate of $2$ feet per second ($2$ ft/s).

Express the distance $d$ between Jason and his brother Tim in terms of the time $t$.
At what time after Jason begins walking towards Tim are the brothers $200$ feet apart?

Solution

Because the distance between Jason and his brother is decreasing at a constant rate, the graph of the distance versus time is a line. Let’s begin by making a rough sketch of the line. In Figure $\PageIndex{10}$, note that we’ve labeled what are normally the $x$- and $y$-axes with the time $t$ and distance $d$, and we’ve included the units with our labels.

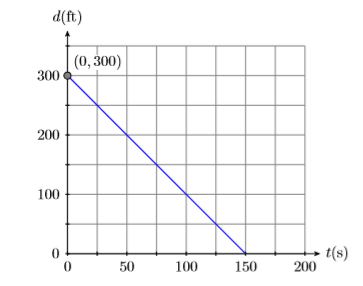
fig 3.4.10.png — Figure $\PageIndex{10}$: A plot of the distance $d$ separating the brothers versus time $t$.

Let $t = 0$ seconds be the time that Jason begins walking towards his brother Tim. At time $t = 0$, the initial distance between the brothers is $300$ feet. This puts the $d$-intercept (normally the $y$-intercept) at the point $(0,300)$ (see Figure $\PageIndex{10}$).

Because Jason is walking toward his brother, the distance between the brothers decreases at a constant rate of $2$ feet per second. This means the line must slant downhill, making the slope negative, so $m = −2$ ft/s. We can construct an accurate plot of distance versus time by starting at the point $(0,300)$, then descending $\Delta d=-300$, then moving to the right $\Delta t=150$. This makes the slope $\Delta d / \Delta t=-300 / 150=-2$ (See Figure $\PageIndex{10}$). Note that the slope is the rate at which the distance $d$ between the brothers is changing with respect to time $t$.

Finally, the equation of the line is $y = mx + b$, where $m$ is the slope of the line and $b$ is the $y$-coordinate (in this case the $d$-coordinate) of the point where the graph crosses the vertical axis. Thus, substitute $−2$ for $m$, and $300$ for $b$ in the slope-intercept form of the line.

\[\begin{aligned} y&= mx+b \quad \color {Red} \text { Slope-intercept form. } \\ y&= -2x+300 \quad \color {Red} \text { Substitute: }-2 \text { for } m, 300 \text { for } b \end{aligned} \nonumber \]

One problem remains. The equation $y = −2x + 300$ gives us $y$ in terms of $x$.

The question required that we express the distance $d$ in terms of the time $t$. So, to finish the solution, replace $y$ with $d$ and $x$ with $t$ (check the axes labels in Figure $\PageIndex{10}$) to obtain a solution: \[d=-2t+300 \nonumber \]
Now that our equation expresses the distance between the brothers in terms of time, let’s answer part (b), “At what time after Jason begins walking towards Tim are the brothers $200$ feet apart?” To find this time, substitute $200$ for $d$ in the equation $d =−2t + 300$, then solve for $t$.\[\begin{aligned} d &= -2t+300 \quad \color {Red} \text { Distance equation } \\ 200 &= -2t+300 \quad \color {Red} \text { Substitute } 200 \text { for } d \end{aligned} \nonumber \]Solve this last equation for the time $t$.\[\begin{aligned} 200-300&= -2t+300-300 \quad \color {Red} \text { Subtract } 300 \text { from both sides. } \\ -100&= -2t \quad \color {Red} \text { Simplify both sides. } \\ \dfrac{-100}{-2}&= \dfrac{-2 t}{-2} \quad \color {Red} \text { Divide both sides by }-2 \\ 50&= t \quad \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]Thus, it takes Jason $50$ seconds to close the distance between the brothers to $200$ feet.

Exercise $\PageIndex{4}$

A swimmer is $50$ feet from the beach, and then begins swimming away from the beach at a constant rate of $1.5$ feet per second ($1.5$ ft/s). Express the distance $d$ between the swimmer and the beach in terms of the time $t$.

Answer: $d=1.5 t+50$