3.5: Forma Punto-Pendiente de una Línea

Última actualización
Guardar como PDF

Page ID: 111562

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la sección anterior aprendimos que si se nos proporciona la pendiente de una línea y su$y$ -intercepción, entonces la ecuación de la línea es$y = mx + b$, donde$m$ está la pendiente de la línea y$b$ es la$y$ -coordenada de la$y$ -intercepción de la línea.

No obstante, ¿supongamos que se desconoce la$y$ -intercepción? En cambio, supongamos que se nos da un punto$(x_0,y_0)$ en la línea y también se nos dice que la pendiente de la línea es m (ver Figura$\PageIndex{1}$).

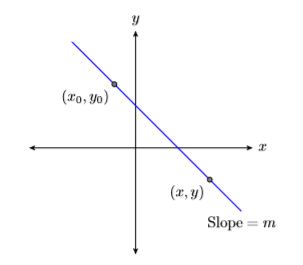
higo 3.5.1.png — Figura$\PageIndex{1}$: Una línea a través del punto$(x_0,y_0)$ con pendiente$m$.

Dejar$(x,y)$ ser un punto arbitrario en la línea, luego utilizar los puntos$(x_0,y_0)$ y$(x,y)$ para calcular la pendiente de la línea.

\[\begin{aligned} \text { Slope }&= \dfrac{\Delta y}{\Delta x} \quad \color{Red} \text { The slope formula. } \\ m&= \dfrac{y-y_{0}}{x-x_{0}} \quad \color{Red} \text { Substitute } m \text { for the slope. Use }(x, y) \text { and }\left(x_{0}, y_{0}\right) \text { to calculate the difference in } y \text { and the difference in } x \end{aligned} \nonumber \]

Despeja las fracciones de la ecuación multiplicando ambos lados por el denominador común.

\[\begin{aligned} m\left(x-x_{0}\right)&= \left[\dfrac{y-y_{0}}{x-x_{0}}\right]x-x_{0} \quad \color{Red} \text { Multiply both sides by } x-x_{0} \\ m\left(x-x_{0}\right)&= y-y_{0} \qquad \qquad \color{Red} \text { Cancel. } \end{aligned} \nonumber \]

Así, la ecuación de la línea es$y−y_0 = m(x−x-0)$.

La forma Punto-Pendiente de una línea

La ecuación de la línea con pendiente m que pasa por el punto$\left(x_{0}, y_{0}\right)$ es:\[y-y_{0}=m\left(x-x_{0}\right) \nonumber \]

Ejemplo$\PageIndex{1}$

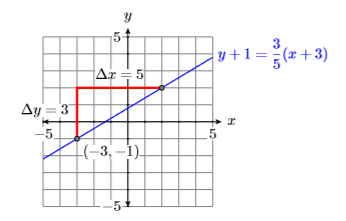
Dibuja la línea que pasa por el punto$(−3,−1)$ que tiene pendiente$3/5$, luego etiquégala con su ecuación.

Solución

Trazar el punto$(−3,−1)$, luego mover$3$ las unidades hacia arriba y$5$ las unidades a la derecha (ver Figura$\PageIndex{2}$). Para encontrar la ecuación, sustituya$(x_0,y_0)$ y$(−3,−1)$$3/5$ por m en la forma punto-pendiente de la línea.

\[\begin{aligned} {y-y_{0}} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-(-1) &= \dfrac{3}{5}(x-(-3)) \quad \color{Red} \text { Substitute: } 3 / 5 \text { for } m,-3 \text { for } x_{0}, \text { and }-1 \text { for } y_{0} \end{aligned} \nonumber \]

Simplificando, la ecuación de la línea es$y+1=\dfrac{3}{5}(x+3)$.

higo 3.5.2.png — Figura$\PageIndex{2}$: La línea que pasa a través$(−3,−1)$ con pendiente$3/5$.

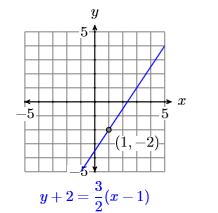
Ejercicio$\PageIndex{1}$

Dibuja la línea que pasa por el punto$(1,−2)$ that has slope $3/2$, then label it with its equation.

Responder: $Ejercicio 3.5.1.png$

En este punto, puede estar haciendo la pregunta “¿Cuándo debo usar el formulario slopintercept y cuándo debo usar el formulario de pendiente puntual?” Aquí hay una buena propina.

Consejo: ¿Qué forma debo usar?

El formulario que debe seleccionar depende de la información proporcionada.

Si se le da la$y$ -intercepción y la pendiente, utilice$y = mx + b$.
Si se le da un punto y la pendiente, utilice$y−y_0 = m(x−x_0)$.

Ejemplo$\PageIndex{2}$

Encuentra la ecuación de la línea que pasa por los puntos$P(−1,2)$ y$Q(3,−4)$.

Solución

Primero, traza los puntos$P(−1,2)$$Q(3,−4)$ y dibuja una línea a través de ellos (ver Figura$\PageIndex{3}$).

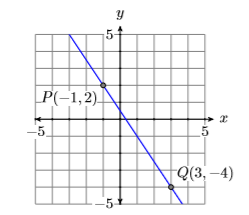
higo 3.5.3.png — Figura$\PageIndex{3}$: La línea que pasa por$P(−1,2)$ y$Q(3,−4)$.

A continuación, calculemos la pendiente de la línea restando las coordenadas del punto$P(−1,2)$ de las coordenadas del punto$Q(3,−4)$.

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-4-2}{3-(-1)} \\ &=\dfrac{-6}{4} \\ &=-\dfrac{3}{2} \end{aligned} \nonumber \]

Así, la pendiente es$−3/2$.

A continuación, utilice la forma punto-pendiente$y−y_0 = m(x−x_0)$ para determinar la ecuación de la línea. Está claro que debemos sustituir la$−3/2$ forma. Pero, ¿cuál de los dos puntos debemos usar? Si usamos el punto$P(−1,2)$ para$(x_0,y_0)$, obtenemos la respuesta a la izquierda, pero si usamos el punto$Q(3,−4)$ para$(x_0,y_0)$, obtenemos la respuesta a la derecha.

$y-2=-\dfrac{3}{2}(x-(-1)) \qquad$o$\qquad y-(-4)=-\dfrac{3}{2}(x-3)$

A primera vista, estas respuestas no tienen el mismo aspecto, pero vamos a examinarlas un poco más de cerca, resolviendo$y$ para poner cada una en forma de pendiente-intercepción. Empecemos con la ecuación de la izquierda.

\ [\ begin {alineado}
y-2 &= -\ dfrac {3} {2} (x- (-1))\ quad\ color {Rojo}\ texto {Usando} m=-3/2\ texto {y}\ izquierda (x_ {0}, y_ {0}\ derecha) = (-1,2)\
y-2 &= -\ dfrac {3} {2} (x+1)\ quad\ color {Rojo}\ texto {Simplificar.}\\
y-2 &= -\ dfrac {3} {2} x-\ dfrac {3} {2}\ quad\ color { Rojo}\ texto {Distribuir} -3/2\\
y-2+2 &= -\ dfrac {3} {2} x-\ dfrac {3} {2} +2\ quad\ color {Rojo}\ texto {Agregar} 2\ texto {a ambos lados.}\\
y &= -\ dfrac {3} {2} {2} x-\ dfrac {3} {2} +\ dfrac ac {4} {2}\ quad\ color {Rojo}\ texto {A la izquierda, simplifique. A la derecha, haz fracciones equivalentes con un denominador común.}\\
y &= -\ dfrac {3} {2} x+\ dfrac {1} {2}\ quad\ color {Rojo}\ text {Simplificar.}
\ end {alineado}\ nonumber\]

Pongamos la segunda ecuación en forma de pendiente-intercepción.

Nota

Tenga en cuenta que la forma$y=-\dfrac{3}{2} x+\dfrac{1}{2}$, cuando se compara con la forma general pendiente-intercepción$y = mx + b$, indica que la$y$ -intercepción es$(0,1/2)$. Examine la figura$\PageIndex{3}$. ¿Pareciera que la$y$ -intercepción es$(0,1/2)$?

\ [\ begin {alineado}
y- (-4) &= -\ dfrac {3} {2} (x-3)\ quad\ color {Rojo}\ texto {Usando} m=-3/2\ texto {y}\ izquierda (x_ {0}, y_ {0}\ derecha) = (3, -4)\
y+4 &= -\ dfrac {3} {2} (x-3)\ quad\ color {Rojo}\ texto {Simplificar.}\\
y+4 &= -\ dfrac {3} {2} x+\ dfrac {9} {2}\ quad\ color { Rojo}\ texto {Distribuir} -3/2\\
y+4-4 &= -\ dfrac {3} {2} {2} x+\ dfrac {9} {2} -4\ quad\ color {Rojo}\ texto {Restar} 4\ texto {de ambos lados.}\\
y &= -\ dfrac {3} {2} {2} x +\ dfrac {9} {2} -\ dfrac {8} {2}\ quad\ color {Rojo}\ texto {A la izquierda, simplifica. A la derecha, haz fracciones equivalentes con un denominador común.}\\
y &= -\ dfrac {3} {2} x+\ dfrac {1} {2}
\ end {alineado}\ nonumber\]

Así, ambas ecuaciones simplifican a la misma respuesta,$y=-\dfrac{3}{2} x+\dfrac{1}{2}$. Esto quiere decir que las ecuaciones$y-2=-\dfrac{3}{2}(x-(-1))$ y$y-(-4)=-\dfrac{3}{2}(x-3)$, aunque se vean diferentes, son las mismas.

Ejercicio$\PageIndex{2}$

Encuentra la ecuación de la línea que pasa por los puntos$P(−2,1)$ and $Q(4,−1)$.

Responder: $y=-\dfrac{1}{3} x+\dfrac{1}{3}$

Ejemplo$\PageIndex{2}$ da lugar al siguiente consejo.

propina

Al encontrar la ecuación de una línea a través de dos puntos$P$ y$Q$, puede sustituir cualquiera de los puntos$P$ o$Q$ por$(x_0,y_0)$ en la forma de punto-pendiente$y−y_0 = m(x−x_0)$. Los resultados parecen diferentes, pero ambos son ecuaciones de la misma línea.

Líneas Paralelas

Recordemos que la pendiente es un número que mide la inclinación de la línea. Si dos líneas son paralelas (nunca se cruzan), tienen la misma pendiente.

Líneas paralelas

Si dos líneas son paralelas, tienen la misma pendiente.

Ejemplo$\PageIndex{3}$

Dibuje la línea$y=\dfrac{3}{4} x-2$ y, a continuación, esboce la línea que pasa por el punto$(−1,1)$ that is parallel to the line $y=\dfrac{3}{4} x-2$. Encuentra la ecuación de esta línea paralela.

Solución

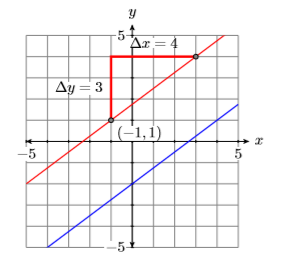
Tenga en cuenta que$y=\dfrac{3}{4} x-2$ está en forma de pendiente-intercepción$y = mx+b$. De ahí que su pendiente sea$3/4$ y su$y$ -intercepción es$(0,−2)$. Trace la$y$ -intercepción$(0,−2)$, mueva$3$ unidades hacia arriba,$4$ unidades derechas, luego dibuje la línea (ver Figura$\PageIndex{4}$).

higo 3.5.4.png — Figura$\PageIndex{4}$: La línea$y=\dfrac{3}{4} x-2$.

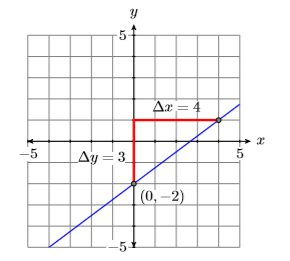
La segunda línea debe ser paralela a la primera, por lo que debe tener la misma pendiente$3/4$. Trace el punto$(−1,1)$, mueva$3$ unidades hacia arriba,$4$ unidades derechas, luego dibuje la línea (vea la línea roja en la Figura$\PageIndex{5}$).

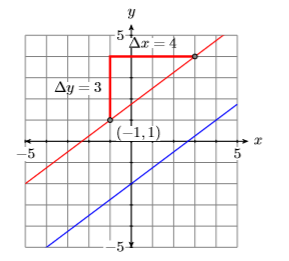
higo 3.5.5.png — Figura$\PageIndex{5}$: Adición de una línea paralela a$y=\dfrac{3}{4} x-2$.

Para encontrar la ecuación de la línea roja paralela en la Figura$\PageIndex{5}$, utilice la forma de pendiente de punto, sustituya$3/4$$m$, luego$(−1,1)$ por$(x_0,y_0)$. Es decir, sustituto$−1$ de$x_0$ y$1$ para$y_0$.

\[\begin{aligned} y-y_{0}&= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-1&= \dfrac{3}{4}(x-(-1)) \quad \color{Red} \text { Substitute: } 3 / 4 \text { for } m,-1 \text { for } x_{0} \text { and } 1 \text { for } y_{0} \\ y-1&= \dfrac{3}{4}(x+1) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Comprobar: En este ejemplo, no estábamos obligados a resolver para$y$, así podemos ahorrarnos algún trabajo de comprobación escribiendo la ecuación

$y-1=\dfrac{3}{4}(x+1) \qquad$en la forma$\qquad y=\dfrac{3}{4}(x+1)+1$

sumando$1$ a ambos lados de la primera ecuación.

A continuación, ingrese cada ecuación como se muestra en la Figura$\PageIndex{6}$, luego cambie el ajuste VENTANA como se muestra en la Figura$\PageIndex{7}$.

higo 3.5.6.png — Figura$\PageIndex{6}$: Ingresar ecuaciones de líneas paralelas.

higo 3.5.7.png — Figura$\PageIndex{7}$: Ajuste los parámetros de **VENTANA** como se muestra.

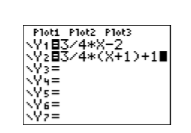
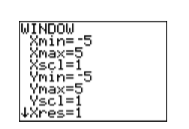
A continuación, presione el botón GRAPAR, seleccione 5:ZSquare para producir la imagen en la Figura$\PageIndex{9}$.

higo 3.5.8.png — Figura$\PageIndex{8}$: Líneas paralelas dibujadas a mano.

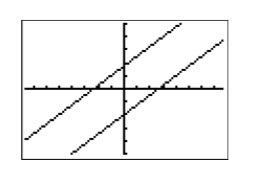
higo 3.5.9.png — Figura$\PageIndex{9}$: Presione el botón GRAPAR y luego seleccione **5:ZSquare** para producir esta imagen.

Observe la estrecha correlación de las líneas de la calculadora en la Figura$\PageIndex{9}$ con las líneas dibujadas a mano en la Figura$\PageIndex{8}$. Esto nos da la certeza de que hemos capturado la respuesta correcta.

Ejercicio$\PageIndex{3}$

Encuentra la ecuación de la línea que pasa por el punto$(2,−3)$ and is parallel to the line$y=\dfrac{3}{4} x+2$.

Responder: $y=\dfrac{3}{2} x-6$

Líneas perpendiculares

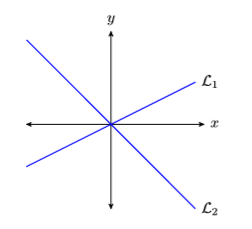
Dos líneas son perpendiculares si se encuentran y forman un ángulo recto ($90$grados). Por ejemplo, las líneas$\mathcal{L}_{1}$ y$\mathcal{L}_{2}$ en Figura$\PageIndex{10}$ son perpendiculares, pero las líneas$\mathcal{L}_{1}$ y$\mathcal{L}_{2}$ en Figura no$\PageIndex{11}$ son perpendiculares.

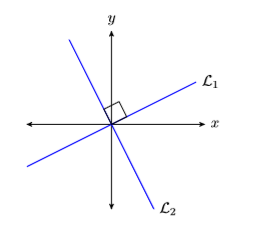
higo 3.5.10.png — Figura$\PageIndex{10}$: Las líneas$\mathcal{L}_{1}$ y$\mathcal{L}_{2}$ son perpendiculares. Se encuentran y forman un ángulo recto ($90$grados).

higo 3.5.11.png — Figura$\PageIndex{11}$: Las líneas$\mathcal{L}_{1}$ y **no$\mathcal{L}_{2}$** son perpendiculares. No forman un ángulo recto ($90$grados).

Antes de continuar, necesitamos establecer una relación entre las pendientes de dos líneas perpendiculares. Entonces, consideremos las líneas perpendiculares$\mathcal{L}_{1}$ y$\mathcal{L}_{2}$ en la Figura$\PageIndex{12}$.

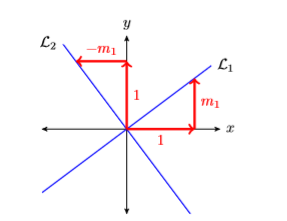
higo 3.5.12.png — Figura$\PageIndex{12}$: Líneas perpendiculares$\mathcal{L}_{1}$ y$\mathcal{L}_{2}$.

Nota

Si tuviéramos que girar la línea$\mathcal{L}_{1}$ noventa grados en sentido contrario a las agujas del reloj, entonces se$\mathcal{L}_{1}$ alinearía con la línea$\mathcal{L}_{2}$, al igual que los triángulos rectos revelando sus pendientes.
$\mathcal{L}_{1}$tiene pendiente$\dfrac{\Delta y}{\Delta x}=\dfrac{m_{1}}{1}=m_{1}$.
$\mathcal{L}_{2}$tiene pendiente$\dfrac{\Delta y}{\Delta x}=\dfrac{1}{-m_{1}}=-\dfrac{1}{m_{1}}$

Pendientes de líneas perpendiculares

Si$\mathcal{L}_{1}$ y$\mathcal{L}_{2}$ son líneas perpendiculares y$\mathcal{L}_{1}$ tiene pendiente$m_1$, la$\mathcal{L}_{2}$ tiene pendiente$−1/m_1$. Es decir, la pendiente de$\mathcal{L}_{2}$ es el recíproco negativo de la pendiente de$\mathcal{L}_{1}$.

Ejemplos:

Para encontrar la pendiente de una línea perpendicular, invertir la pendiente de la primera línea y negar.

Si la pendiente de$\mathcal{L}_{1}$ es$2$, entonces la pendiente de la línea perpendicular$\mathcal{L}_{2}$ es$−1/2$.
Si la pendiente de$\mathcal{L}_{1}$ es$−3/4$, entonces la pendiente de la línea perpendicular$\mathcal{L}_{2}$ es$4/3$.

Ejemplo$\PageIndex{4}$

Dibuje la línea y$y=-\dfrac{2}{3} x-3$, a continuación, esboce la línea a través$(2,1)$ de la cual es perpendicular a la línea$y=-\dfrac{2}{3} x-3$ Encuentra la ecuación de esta línea perpendicular.

Solución

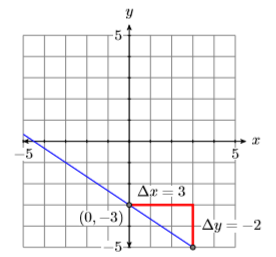
Tenga en cuenta que$y=-\dfrac{2}{3} x-3$ está en forma de pendiente-intercepción$y = mx+b$. De ahí que su pendiente sea$−2/3$ y su$y$ -intercepción es$(0,−3)$. Trace la$y$ -intercepción$(0,−3)$, mueva$3$ las unidades a la derecha, hacia abajo dos unidades, luego dibuje la línea (ver Figura$\PageIndex{13}$).

higo 3.5.13.png — Figura$\PageIndex{13}$: La línea$y=-\dfrac{2}{3} x-3$.

Debido a que la línea$y=-\dfrac{2}{3} x-3$ tiene pendiente$−2/3$, la pendiente de la línea perpendicular a esta línea será el recíproco negativo de$−2/3$, es decir$3/2$. Así, para dibujar la línea perpendicular, comience en el punto dado$(2 ,1)$, mueva hacia arriba$3$ las unidades, las$2$ unidades derechas, luego dibuje la línea (ver Figura$\PageIndex{14}$).

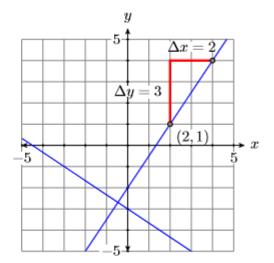
higo 3.5.14.png — Figura$\PageIndex{14}$: Adición de una línea perpendicular a$y=-\dfrac{2}{3} x-3$.

Para encontrar la ecuación de la línea perpendicular en la Figura$\PageIndex{14}$, utilice la forma de pendiente de punto, sustituya$3/2$$m$, luego$(2 ,1)$ por$(x_0,y_0)$. Es decir, sustituir$2$$x_0$, entonces$1$ para$y_0$.

\[\begin{aligned} y-y_{0}&= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-1&= \dfrac{3}{2}(x-2) \quad \color{Red} \text { Substitute: } 3 / 2 \text { for } m, 2 \text { for } x_{0} \text { and } 1 \text { for } y_{0} \end{aligned} \nonumber \]

Comprobar: En este ejemplo, no estábamos obligados a resolver para$y$, así podemos ahorrarnos algún trabajo de comprobación escribiendo la ecuación

$y-1=\dfrac{3}{2}(x-2) \qquad$en la forma$\quad y=\dfrac{3}{2}(x-2)+1$

sumando$1$ a ambos lados de la primera ecuación. A continuación, ingrese cada ecuación como se muestra en la Figura$\PageIndex{15}$, luego seleccione 6:ZStandard para producir la imagen en la Figura$\PageIndex{16}$.

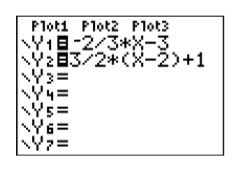
higo 3.5.15.png — Figura$\PageIndex{15}$: Ingresar ecuaciones de líneas perpendiculares.

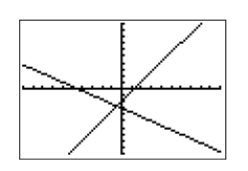
higo 3.5.16.png — Figura$\PageIndex{16}$: **6:ZStandard** produce dos líneas que no se ven perpendiculares.

Tenga en cuenta que las líneas de la Figura$\PageIndex{16}$ no parecen ser perpendiculares. ¿Hemos hecho algo mal? ¡La respuesta es no! El hecho de que la pantalla de visualización de la calculadora sea más ancha que alta está distorsionando el ángulo en el que se encuentran las líneas.

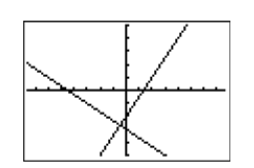
Para que el resultado de la calculadora coincida con el resultado de la Figura$\PageIndex{14}$, cambie la configuración de la ventana como se muestra en la Figura$\PageIndex{17}$, luego seleccione 5:ZSquare en el menú ZOOM para producir la imagen en la Figura$\PageIndex{18}$. Observe la estrecha correlación de las líneas de la calculadora en la Figura$\PageIndex{18}$ con las líneas dibujadas a mano en la Figura$\PageIndex{14}$. Esto nos da la certeza de que hemos capturado la respuesta correcta.

higo 3.5.17.png — Figura$\PageIndex{17}$: Cambiar los parámetros de **VENTANA** como se muestra.

higo 3.5.18.png — Figura$\PageIndex{18}$: **5:ZSquare** produce dos líneas que sí se ven perpendiculares.

Ejercicio$\PageIndex{4}$

Encuentra la ecuación de la línea que pasa por el punto$(−3,1)$ and is perpendicular to the line $y=-\dfrac{1}{2} x+1$.

Responder: $y=2 x+7$

Aplicaciones

Veamos una aplicación de líneas en el mundo real.

Ejemplo$\PageIndex{5}$

El agua se congela a$32^{\circ} \mathrm{F}$ (Fahrenheit) y a$0^{\circ} \mathrm{C}$ (Celsius). El agua hierve en$212^{\circ} \mathrm{F}$ y en$100^{\circ} \mathrm{C}$. Si la relación es lineal, encontrar una ecuación que exprese la temperatura Celsius en términos de la temperatura Fahrenheit. Utilice el resultado para determinar la temperatura Celsius cuando la temperatura Fahrenheit es$113^{\circ} \mathrm{F}$.

Solución

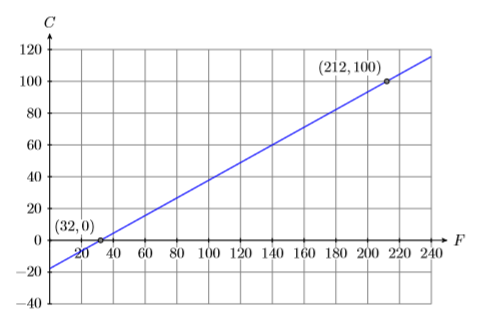
En este ejemplo, la temperatura Celsius depende de la temperatura de Fahrenheit. Esto hace que la temperatura Celsius sea la variable dependiente y se coloca en el eje vertical. Esta temperatura Fahrenheit es la variable independiente, por lo que se coloca en el eje horizontal (ver Figura$\PageIndex{19}$).

A continuación, el agua se congela en$32^{\circ} \mathrm{F}$ y$0^{\circ} \mathrm{C}$, dándonos el punto$(F,C) = (32,0)$. En segundo lugar, el agua hierve en$212^{\circ} \mathrm{F}$ y$100^{\circ} \mathrm{C}$, dándonos el punto$(F,C)= (212,100)$. Observe cómo hemos escalado los ejes para que cada uno de estos puntos fit en el sistema de coordenadas. Finalmente, asumiendo una relación lineal entre las temperaturas Celsius y Fahrenheit, trazar una línea a través de estos dos puntos (ver Figura$\PageIndex{19}$).

higo 3.5.19.png — Figura$\PageIndex{19}$: La relación lineal entre la temperatura Celsius y Fahrenheit.

Calcular la pendiente de la línea.

\[\begin{aligned} m&= \dfrac{\Delta C}{\Delta F} \quad \color{Red} \text { Slope formula. } \\ m&= \dfrac{100-0}{212-32} \quad \color{Red} \text { Use the points }(32,0) \text { and }(212,100) \text { to compute the difference in C and F}\\ m&= \dfrac{100}{180} \quad \color{Red} \text { Simplify. } \\ m&= \dfrac{5}{9} \quad \color{Red} \text { Reduce. } \end{aligned} \nonumber \]

Se puede utilizar$(32,0)$ o$(212,100)$ en forma de pendiente puntual. El punto$(32,0)$ tiene números menores, por lo que parece más fácil de sustituir$(x_0,y_0) = (32 ,0)$ y$m =5 /9$ en la forma punto-pendiente$y−y_0 = m(x−x_0)$.

\[\begin{aligned} y-y_{0}=& m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-0 &=\dfrac{5}{9}(x-32) \quad \color{Red} \text { Substitute: } 5 / 9 \text { for } m, 32 \text { for } x_{0}, \text { and } 0 \text { for } y_{0} \\ y &=\dfrac{5}{9}(x-32) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Sin embargo, nuestros ejes vertical y horizontal están etiquetados$C$ y$F$ (ver Figura$\PageIndex{19}$) respectivamente, por lo que debemos reemplazar$y$ con$C$ y$x$ con$F$ para obtener una ecuación que exprese la temperatura Celsius$C$ en términos de Fahrenheit temperatura$F$.

\[C=\dfrac{5}{9}(F-32) \label{temperature} \]

Finalmente, para encontrar la temperatura Celsius cuando la temperatura Fahrenheit es$113^{\circ} \mathrm{F}$, sustituya$113$$F$ en la Ecuación\ ref {temperatura}

\[\begin{aligned} C&= \dfrac{5}{9}(F-32) \quad \color{Red} \text { Equation }(3.5.1) \\ C&= \dfrac{5}{9}(113-32) \quad \color{Red} \text { Substitute: } 113 \text { for } F \\ C&= \dfrac{5}{9}(81) \quad \color{Red} \text { Subtract. } \\ C&= 45 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Por lo tanto, si la temperatura Fahrenheit es$113^{\circ} \mathrm{F}$, entonces la temperatura Celsius es$45^{\circ} \mathrm{C}$.

Ejercicio$\PageIndex{5}$

Encuentra una ecuación que exprese la temperatura Fahrenheit en términos de la temperatura Celsius. Usa el resultado para encontrar la temperatura Fahrenheit cuando la temperatura Celsius es$25^{\circ} \mathrm{C}$.

Responder: $77^{\circ} \mathrm{F}$