3.6: Forma estándar de una línea

Última actualización
Guardar como PDF

Page ID: 111544

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección investigaremos la forma estándar de una línea. Empecemos con un ejemplo sencillo.

Ejemplo$\PageIndex{1}$

Resolver la ecuación$2x +3y = 6$ para$y$ y trazar el resultado.

Solución

Primero resolvemos la ecuación$2x +3y = 6$ para$y$. Comience aislando todos los términos que contengan y en un lado de la ecuación, moviendo o manteniendo todos los términos restantes en el otro lado de la ecuación.

\[\begin{aligned} 2x+3y &= 6 \quad \color{Red} \text { Original equation. } \\ 2x+3y-2x &= 6-2x \quad \color{Red} \text { Subtract } 2x \text { from both sides. } \\ 3y &= 6-2x \quad \color{Red} \text { Simplify. } \\ \dfrac{3y}{3} &= \dfrac{6-2x}{3} \quad \color{Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]

Nota

Así como la multiplicación es distributiva con respecto a la suma, también\[a(b + c)=ab + ac \nonumber \] lo es la división distributiva con respecto a la suma. \[\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c} \nonumber \]

Al dividir una suma o una diferencia entre un número, usamos la propiedad distributiva y dividimos ambos términos por ese número.

\[\begin{aligned} y &= \dfrac{6}{3}-\dfrac{2x}{3} \quad \color{Red} \text { On the left, simplify. On the right, divide both terms by } 3 \\ y &= 2-\dfrac{2 x}{3} \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Por último, utilice la propiedad conmutativa para cambiar el orden de los términos en el lado derecho del último resultado.

\[\begin{aligned} y &= 2+\left(-\dfrac{2 x}{3}\right) \quad \color{Red} \text { Add the opposite. } \\ y &= -\dfrac{2}{3} x+2 \quad \color{Red} \text { Use the commutative property to switch the order. } \end{aligned} \nonumber \]

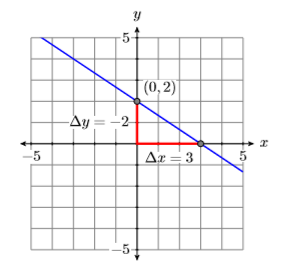
Debido a que la ecuación$2x +3y = 6$ es equivalente a la ecuación$y=-\dfrac{2}{3} x+2$, la gráfica de$2x +3 y = 6$ es una línea, teniendo pendiente$m = −2/3$ e$y$ -intercepción$(0 ,2)$. Por lo tanto, para dibujar la gráfica de$2x+3y = 6$, trazar ellos-interceptar$(0,2)$, mover hacia abajo$2$ y$3$ hacia la derecha, luego dibujar la línea (ver Figura$\PageIndex{1}$).

higo 3.6.1.png — Figura$\PageIndex{1}$: La gráfica de$2x +3y = 6$, o equivalentemente,$y=-\dfrac{2}{3} x+2$

Ejercicio$\PageIndex{1}$

Agrega texto de ejercicios aquí.

Contestar: $Ejercicio 3.6.1.png$

En general, a menos que$B = 0$, siempre podamos resolver la ecuación$Ax + By = C$ para y:

\ [\ begin {aligned}
Ax+By &= C\ quad\ color {Rojo}\ text {Ecuación original.}\\
Ax+By-Ax &= C-Ax\ quad\ color {Rojo}\ text {Restar} Ax\ texto {de ambos lados.}\\
Por &= C-Ax\ quad\ color {Rojo}\ text {Simplificar.}\
\\ dfrac {Por} {B} &=\ dfrac {C-Ax} {B}\ quad\ color {Rojo}\ texto {Divide ambos lados por} B\\
y &=\ dfrac {C} {B} -\ dfrac {Ax} {B}\ quad\ color {Rojo}\ texto {distribuir el} B\\
y &= -\ dfrac {A} {B} {B} x+\ dfrac {C} {B}\ quad\ color {Rojo}\ texto {Propiedad conmutativa}
\ end {alineado}\ nonumber\]

Tenga en cuenta que el último resultado está en forma de pendiente-intercepción$y = mx+b$, cuya gráfica es una línea. Hemos establecido el siguiente resultado.

FACT

La gráfica de la ecuación$Ax + By = C$, es una línea.

Puntos importantes: Un par de comentarios importantes están en orden.

La forma$Ax + By = C$ requiere que los coecients$A$,$B$, y$C$ sean enteros. Entonces, por ejemplo, despejaríamos las fracciones de la forma\[\dfrac{1}{2} x+\dfrac{2}{3} y=\dfrac{1}{4} \nonumber \] multiplicando ambos lados por el mínimo denominador común. \[\begin{aligned} 12\left(\dfrac{1}{2} x+\dfrac{2}{3} y\right) &=\left(\dfrac{1}{4}\right) 12 \\ 6 x+8 y &=3 \end{aligned}\nonumber \]Tenga en cuenta que los coecients son ahora enteros.
La forma$Ax + By = C$ también requiere que el primer ciente no$A$ sea negativo; es decir,$A ≥0$. Así, si tenemos\[-5 x+2 y=6 \nonumber \] entonces multiplicaríamos ambos lados por$−1$, llegando a:\[\begin{aligned}-1(-5 x+2 y) &=(6)(-1) \\ 5 x-2 y &=-6 \end{aligned} \nonumber \] Tenga en cuenta que ahora$A = 5$ es mayor o igual a cero.
Si$A$,$B$, y$C$ tener un divisor común mayor que$1$, se recomienda que dividamos ambos lados por el divisor común, “reduciendo” así los coecients. Por ejemplo, si tenemos\[3x + 12y =−24 \nonumber \] entonces dividir ambos lados por$3$ “reduce” el tamaño de los coecients. \[\begin{aligned} \dfrac{3 x+12 y}{3} &=\dfrac{-24}{3} \\ x+4 y &=-8 \end{aligned} \nonumber \]

Forma estándar

La forma$Ax + By = C$, donde$A$,$B$, y$C$ son enteros, y$A ≥ 0$, se llama la forma estándar de una línea.

Inclinación-Intercepción a Forma Estándar

Ya hemos transformado un par de ecuaciones en forma estándar en forma de slopeintercept. Invierta el proceso y coloquemos una ecuación en forma de intercepción de pendiente en forma estándar.

Ejemplo$\PageIndex{2}$

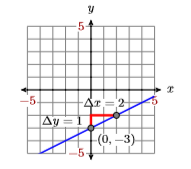
Dada la gráfica de la línea en la Figura$\PageIndex{2}$, encontrar la ecuación Dada la gráfica de la línea de abajo, encontrar la ecuación de la línea en forma estándar.

higo 3.6.2.png — Figura$\PageIndex{2}$: Determinar la ecuación de la línea.

Solución

La línea intercepta el$y$ eje -en$(0,−3)$. De$(0,−3)$, subir$5$ unidades, luego a la izquierda$2$ unidades. Así, la línea tiene pendiente$\Delta y / \Delta x=-5 / 2$ (ver Figura$\PageIndex{3}$). $−5/2$Forma sustituta y$−3$ para$b$ en la forma pendiente-intercepción de la línea.

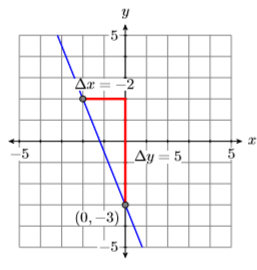
higo 3.6.3.png — Figura$\PageIndex{3}$: La línea tiene$y$ -intercepción$(0,−3)$ y pendiente$−5/2$.

\[\begin{aligned} y &= mx+b \quad \color{Red} \text { Slope-intercept form. } \\ y &= -\dfrac{5}{2} x-3 \quad \color{Red} \text { Substitute: }-5 / 2 \text { for } m,-3 \text { for } b \end{aligned} \nonumber \]

Para poner este resultado en forma estándar$Ax + By = C$, primero borra las fracciones multiplicando ambos lados por el denominador común.

\[\begin{aligned} 2y &= 2\left[-\dfrac{5}{2} x-3\right] \quad \color{Red} \text { Multiply both sides by } 2 \\ 2y &= 2\left[-\dfrac{5}{2} x\right]-2[3] \quad \color{Red} \text { Distribute the } 2 \\ 2y &= -5x-6 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Eso despeja las fracciones. Para poner este último resultado en la forma$Ax+By = C$, necesitamos mover el término$−5x$ al otro lado de la ecuación.

\[\begin{aligned} 5x+2y &= -5x-6+5x \quad \color{Red} \text { Add } 5x \text { to both sides. } \\ 5x+2y &= -6 \quad \color{Red}\text { Simplify. } \end{aligned} \nonumber \]

Así, la forma estándar de la línea es$5x +2y = −6$. Tenga en cuenta que todos los coecients son enteros y los términos están dispuestos en el orden$Ax+By = C$, con$A ≥0$.

Ejercicio$\PageIndex{2}$

Dada la gráfica de la línea de abajo, encontrar la ecuación de la línea en forma estándar.

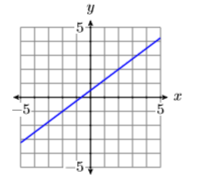
$Ejercicio 3.6.2.png$

Contestar: $3 x−4y = −2$

Forma punto-pendiente a estándar

Hagamos un ejemplo donde tenemos que poner la forma punto-pendiente de una línea en forma estándar.

Ejemplo$\PageIndex{3}$

Dibuje la línea que pasa por los puntos$(−3,−4)$ y$(1,2)$, luego, encuentre la ecuación de la línea en forma estándar.

Solución

Traza los puntos (−3, −4) y (1,2), luego dibuja una línea a través de ellos (ver Figura$\PageIndex{4}$).

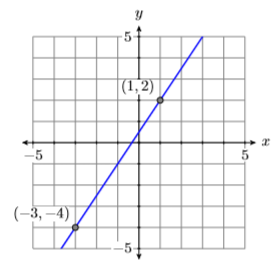
higo 3.6.4.png — Figura$\PageIndex{4}$: La línea a través$(−3,−4)$ y$(1,2)$.

Utilice los puntos$(−3,−4)$ y$(1,2)$ para calcular la pendiente.

\[\begin{aligned} \text { Slope } &= \dfrac{\Delta y}{\Delta x} \quad \color{Red} \text { Slope formula. } \\ &= \dfrac{2-(-4)}{1-(-3)} \quad \color{Red} \text { Subtract coordinates of }(-3,-4) \\ &= \dfrac{6}{4} \quad \text { Simplify. } \\ &= \dfrac{3}{2} \quad \text { Reduce. } \end{aligned} \nonumber \]

Vamos a sustituir$\left(x_{0}, y_{0}\right)=(1,2)$ y$m =3 /2$ en la forma de punto-pendiente de la línea. (Nota: Sustituyendo$\left(x_{0}, y_{0}\right)=(-3,-4)$ y$m =3 /2$ daría la misma respuesta. )

\[\begin{aligned} y-y_{0} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-2 &= \dfrac{3}{2}(x-1) \quad \color{Red} \text { Substitute: } 3 / 2 \text { for } m, 1 \text { for } x_{0} \end{aligned} \nonumber \]

La pregunta solicita que nuestra respuesta final sea presentada en forma estándar. Primero limpiamos las fracciones.

\[\begin{aligned} y-2 &= \dfrac{3}{2} x-\dfrac{3}{2} \quad \color{Red} \text { Distribute the } 3 / 2 \\ 2[y-2] &= 2\left[\dfrac{3}{2} x-\dfrac{3}{2}\right] \quad \color{Red} \text { Multiply both sides by } 2 \\ 2y-2[2] &= 2\left[\dfrac{3}{2} x\right]-2\left[\dfrac{3}{2}\right] \quad \color{Red} \text { Distribute the } 2 \\ 2y-4 &= 3 x-3 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Ahora que hemos despejado las fracciones, debemos ordenar los términos en la forma$Ax+By = C$. Tenemos que mover el término$3x$ al otro lado de la ecuación.

\[\begin{aligned} 2y-4-3x &= 3x-3-3x \quad \color{Red} \text { Subtract } 3 x \text { from both sides. } \\ -3x+2y-4 &= -3 \quad \color{Red} \text { Simplify, changing the order on the left-hand side. } \end{aligned} \nonumber \]

Para poner esto en la forma$Ax + By = C$, necesitamos mover el término$−4$ al otro lado de la ecuación.

\[\begin{aligned} -3x+2y-4+4 &= -3+4 \quad \color{Red} \text { Add } 4 \text { to both sides. } \\ -3x+2y &= 1 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Parece que$−3x+2y = 1$ está en la forma$Ax +By = C$. Sin embargo, la forma estándar lo requiere$A ≥ 0$. Nosotros tenemos$A = −3$. Para fijar esto, multiplicamos ambos lados por$−1$.

\[\begin{aligned} -1[-3x+2y] &= -1[1] \quad \color{Red} \text { Multiply both sides by }-1 \\ 3x-2y &= -1 \quad \color{Red} \text { Distribute the }-1 \end{aligned} \nonumber \]

Así, la ecuación de la línea en forma estándar es$3x−2y =−1$.

Nota

Si no conseguimos reducir la pendiente a términos más bajos, entonces la ecuación de la línea sería:\[y-2=\dfrac{6}{4}(x-1) \nonumber \]

Multiplicar ambos lados por nos$4$ daría el resultado\[4y−8=6x−6 \nonumber \] o equivalentemente:\[−6x +4y =2 \nonumber \]

Esto no parece la misma respuesta, pero si dividimos ambos lados por$−2$, sí obtenemos el mismo resultado. \[3x−2y = −1 \nonumber \]

Esto demuestra la importancia de exigir$A ≥ 0$ y “reducir” a los coecients$A$,$B$, y$C$. Nos permite comparar nuestra respuesta con nuestros compañeros o las respuestas presentadas en este libro de texto.

Ejercicio$\PageIndex{3}$

Encuentra la forma estándar de la ecuación de la línea que pasa por los puntos$(−2,4)$ and $(3,−3)$.

Responder: $7x +5y =6$

Intercepta

Hemos estudiado la$y$ -intercepción, el punto donde la gráfica cruza el$y$ eje -eje, pero igualmente importantes son las$x$ -intercepciones, los puntos donde la gráfica cruza el$x$ eje -eje.

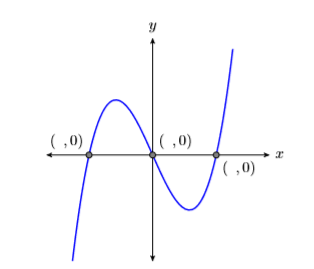
higo 3.6.5.png — Figura$\PageIndex{5}$: Cada$x$ -intercepción tiene una$y$ coordenada -igual a cero.

En la Figura$\PageIndex{5}$, la gráfica cruza el$x$ eje tres veces. A cada uno de estos puntos de cruce se le llama$x$ -intercepción. Tenga en cuenta que cada una de estas$x$ -intercepciones tiene una$y$ coordenada -igual a cero. Esto lleva a la siguiente regla.

$x$Intercepta: Para encontrar las$x$ -intercepciones de la gráfica de una ecuación, sustituirla$y = 0$ en la ecuación y resolver para$x$.

higo 3.6.6.png — Figura$\PageIndex{6}$: Cada$y$ -intercepción tiene una$x$ coordenada -igual a cero.

De igual manera, la gráfica de la Figura$\PageIndex{6}$ cruza el$y$ eje tres veces. A cada uno de estos puntos de cruce se le llama$y$ -intercepción. Tenga en cuenta que cada una de estas$y$ -intercepciones tiene una$x$ coordenada -igual a cero. Esto lleva a la siguiente regla.

$y$Intercepta: Para encontrar las$y$ -intercepciones de la gráfica de una ecuación, sustituirla$x = 0$ en la ecuación y resolver para$y$.

Pongamos a trabajar estas reglas para encontrar intercepciones.

Ejemplo$\PageIndex{4}$

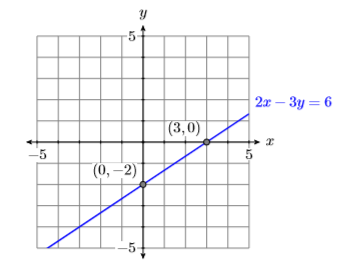
Encuentra las$x$ - y$y$ -intercepciones de la línea que tiene ecuación$2x−3y = 6$. Traza las intercepciones y dibuja la línea.

Solución

Sabemos que la gráfica de$2x−3y = 6$ es una línea. Además, dos puntos determinan completamente una línea. Esto significa que solo necesitamos trazar las$y$ -y$x$ -intercepciones, luego trazar una línea a través de ellas.

Encontrar la$x$ -intercepción de$2x−3y = 6$,$0$ sustituir$y$ y resolver$x$.

\[\begin{aligned} 2 x-3 y &=6 \\ 2 x-3(0) &=6 \\ 2 x &=6 \\ \dfrac{2 x}{2} &=\dfrac{6}{2} \\ x &=3 \end{aligned} \nonumber \]

Así, la$x$ -intercepción de la línea es$(3,0)$.

Encontrar la$y$ -intercepción de$2x−3y = 6$,$0$ sustituir$x$ y resolver$y$.

\[\begin{aligned} 2 x-3 y &=6 \\ 2(0)-3 y &=6 \\-3 y &=6 \\ \frac{-3 y}{-3} &=\frac{6}{-3} \\ y &=-2 \end{aligned} \nonumber \]

Así, la$y$ -intercepción de la línea es$(0,−2)$.

Traza la$x$ -intercepción$(3,0)$ y la$y$ -intercepción$(0,−2)$ y dibuja una línea a través de ellas (ver Figura$\PageIndex{7}$).

higo 3.6.7.png — Figura$\PageIndex{7}$: La gráfica de$2x−3y = 6$ tiene intercepciones$(3,0)$ y$(0,−2)$.

Ejercicio$\PageIndex{4}$

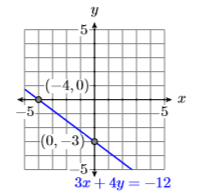
Encuentra las$y$ intercepciones$x$- y de la línea que tiene la ecuación$3x +4y = −12$. Plot the intercepts and draw the line.

Responder

$x$-interceptar:$(−4,0)$

$y$-interceptar:$(0,−3)$

$Ejercicio 3.6.4.png$

Ejemplo$\PageIndex{5}$

Dibuje la línea y$4x +3 y = 12$, a continuación, dibuje la línea a través del punto$(−2,−2)$ que es perpendicular a la línea$4x +3 y = 12$. Encuentra la ecuación de esta línea perpendicular.

Solución

Encontremos primero las -y$x$$y$ -intercepciones de la línea$4x +3y = 12$.

Para encontrar la$x$ -intercepción de la línea$4x+3y = 12$, sustituir$0$$y$ y resolver$x$.

\[\begin{aligned} 4 x+3 y &=12 \\ 4 x+3(0) &=12 \\ 4 x &=12 \\ \dfrac{4 x}{4} &=\dfrac{12}{4} \\ x &=3 \end{aligned} \nonumber \]

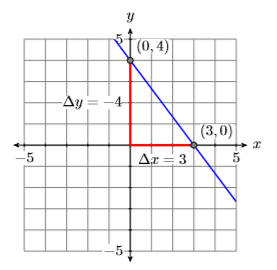
Así, la$x$ -intercepción de la línea es$(3,0)$.

Para encontrar la$y$ -intercepción de la línea$4x+3y = 12$, sustituir$0$$x$ y resolver$y$.

\[\begin{aligned} 4 x+3 y &=12 \\ 4(0)+3 y &=12 \\ 3 y &=12 \\ \dfrac{3 y}{3} &=\dfrac{12}{3} \\ y &=4 \end{aligned} \nonumber \]

Así, la$y$ -intercepción de la línea es$(0,4)$.

Traza las intercepciones y dibuja una línea a través de ellas. Obsérvese que queda claro a partir de la gráfica que la pendiente de la línea$3x +4y = 12$ es$−4/3$ (ver Figura$\PageIndex{8}$).

higo 3.6.8.png — Figura$\PageIndex{8}$: La gráfica de$4x+3y = 12$ tiene intercepciones$(3,0)$$(0,4)$ y pendiente$−4/3$.

También se podría resolver la forma de intercepción de$y$ to put $3x +4 y = 12$ in taludes para determinar la pendiente.

Debido a que la pendiente de$3x+4y = 12$ es$−4/3$, la pendiente de una línea perpendicular a$3x +4y = 12$ será el recíproco negativo de$−4/3$, es decir$3/4$. Nuestra línea perpendicular tiene que pasar por el punto$(−2,−2)$. Comience en$(−2,−2)$, mueva$3$ las unidades hacia arriba, luego$4$ las unidades a la derecha, luego dibuje la línea. Debe parecer perpendicular a la línea$3x +4y = 12$ (ver Figura$\PageIndex{9}$).

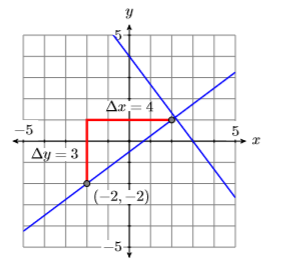
higo 3.6.9.png — Figura$\PageIndex{9}$: La pendiente de la línea perpendicular es el recíproco negativo de$−4/3$, a saber$3/4$.

Finalmente, utilice la forma punto-pendiente$m =3 /4$,, y$\left(x_{0}, y_{0}\right)=(-2,-2)$ para determinar la ecuación de la línea perpendicular.

\[\begin{aligned} y-y_{0} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-(-2) &= \dfrac{3}{4}(x-(-2)) \quad \color{Red} \text { Substitute: } 3 / 4 \text { for } m,-2 \text { for } x_{0} \text { and }-2 \text { for } y_{0} \\ y+2 &= \dfrac{3}{4}(x+2) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Coloquemos nuestra respuesta en forma estándar. Despeja las fracciones.

\[\begin{aligned} y+2 &= \dfrac{3}{4} x+\dfrac{6}{4} \quad \color{Red} \text { Distribute } 3 / 4 \\ 4[y+2] &= 4\left[\dfrac{3}{4} x+\dfrac{6}{4}\right] \quad \color{Red} \text { Multiply both sides by } 4 \\ 4y+4[2] &= 4\left[\dfrac{3}{4} x\right]+4\left[\dfrac{6}{4}\right] \quad \color{Red} \text { Distribute the } 4 \\ 4y+8 &= 3x+6 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Reorganizar los términos para ponerlos en el orden$Ax + By = C$.

\[\begin{aligned} 4y+8-3x &= 3x+6-3x \quad \color{Red} \text { Subtract } 3x \text { from both sides. } \\ -3x+4y+8 &= 6 \quad \color{Red} \text { Simplify. Rearrange on the left. } \\ -3x+4y+8-8 &= 6-8 \quad \color{Red} \text { Subtract } 8 \text { from both sides. } \\ -3x+4y &= -2 \quad \color{Red} \text { Simplify. } \\ -1(-3x+4y) &= -1(-2) \quad \color{Red} \text { Multiply both sides by }-1 \\ 3x-4y &= 2 \quad \color{Red} \text { Distribute the }-1 \end{aligned} \nonumber \]

De ahí que la ecuación de la línea perpendicular sea$3x−4y = 2$.

Ejercicio$\PageIndex{5}$

Encuentra la ecuación de la línea que pasa por el punto$(3,2)$ and is perpendicular to the line $6x−5y = 15$.

Responder: $5x +6y = 27$

Líneas horizontales y verticales

Aquí mantenemos una promesa anterior de abordar lo que sucede con el formulario estándar$Ax + By = C$ cuando cualquiera$A = 0$ o$B = 0$. Por ejemplo, la forma$3x = 6$, cuando se compara con la forma estándar$Ax + By = C$, tiene$B = 0$. De igual manera, la forma$2y = −12$, cuando se compara con la forma estándar$Ax + By = C$, tiene$A = 0$. Por supuesto, se$3 x = 6$ puede simplificar$x = 2$ y$2 y = −12$ puede simplificarse para$y = −6$. Así, si cualquiera$A = 0$ o$B = 0$, la forma estándar Ax + By = C toma la forma$x = a$ y$y = b$, respectivamente.

Como veremos en el siguiente ejemplo, la forma$x = a$ produce una línea vertical, mientras que la forma$y = b$ produce una línea horizontal.

Ejemplo$\PageIndex{6}$

Dibuje las gráficas de$x = 3$ y$y = −3$.

Solución

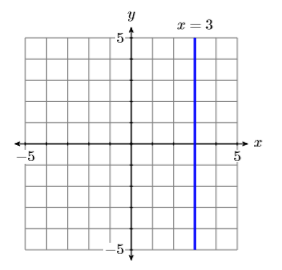
Para bosquejar la gráfica de$x = 3$, recordemos que la gráfica de una ecuación es el conjunto de todos los puntos que satisfacen la ecuación. De ahí que para dibujar la gráfica de$x = 3$, debemos trazar todos los puntos que satisfagan la ecuación$x = 3$; es decir, debemos trazar todos los puntos que tengan una$x$ coordenada igual a$3$. El resultado se muestra en la Figura$\PageIndex{10}$.

higo 3.6.10.png — Figura$\PageIndex{10}$: La gráfica de$x = 3$ es una línea vertical.

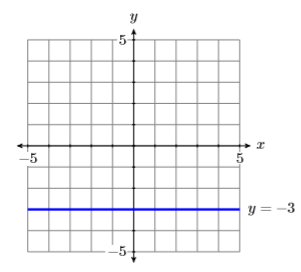
En segundo lugar, para bosquejar la gráfica de$y = −3$, trazamos todos los puntos teniendo una$y$ coordenada igual a$−3$. El resultado se muestra en la Figura$\PageIndex{11}$.

higo 3.6.11.png — Figura$\PageIndex{11}$: La gráfica de$y =−3$ es una línea horizontal.

Cosas a tener en cuenta:

Un par de comentarios están en orden respecto a las líneas en Figuras$\PageIndex{10}$ y$\PageIndex{11}$.

La gráfica de$x = 3$ en Figura$\PageIndex{10}$, al ser una línea vertical, tiene pendiente sin definir. Por lo tanto, no podemos usar ni una de las fórmulas$y = mx + b$ ni$y−y_0 = m(x−x_0)$ para obtener la ecuación de la línea. La única forma en que podemos obtener la ecuación es notar que la línea es el conjunto de todos los puntos$(x,y)$ cuya$x$ coordenada es igual$3$.
Sin embargo, la gráfica de$y = −3$, al ser una línea horizontal, tiene pendiente cero, por lo que podemos usar la forma pendiente-intercepción para encontrar la ecuación de la línea. Tenga en cuenta que la$y$ -intercepción de esta gráfica es$(0,−3)$. Si sustituimos estos números en$y = mx + b$, obtenemos:\[\begin{aligned} y &= mx+b \quad \color{Red} \text { Slope-intercept form. } \\ y &= 0x+(-3) \quad \color{Red} \text { Substitute: } 0 \text { for } m,-3 \text { for } b \\ y &= -3 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

No obstante, es mucho más fácil simplemente mirar la línea en Figuras$\PageIndex{11}$ y señalar que es la colección de todos los puntos$(x,y)$ con$y = 3$.

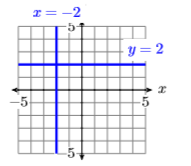
Ejercicio$\PageIndex{6}$

Dibuje las gráficas de$x = −2$ y$y = 2$.

Responder: $Ejercicio 3.6.6.png$