4.1: Resolver sistemas mediante gráficos

En esta sección se introduce una técnica gráfica para resolver sistemas de dos ecuaciones lineales en dos incógnitas. Como vimos en el capítulo anterior, si un punto satisface una ecuación, entonces ese punto se encuentra en la gráfica de la ecuación. Si estamos buscando un punto que satisfaga dos ecuaciones, entonces estamos buscando un punto que se encuentre en las gráficas de ambas ecuaciones; es decir, estamos buscando un punto de intersección.

Por ejemplo, considere las dos ecuaciones:

\[\begin{aligned} x-3 y &=-9 \\ 2 x+3 y &=18 \end{aligned} \nonumber \]

que se llama un sistema de ecuaciones lineales. Las ecuaciones son ecuaciones lineales porque sus gráficas son líneas, como se muestra en la Figura\(\PageIndex{1}\). Obsérvese que las dos líneas de la Figura se\(\PageIndex{1}\) cruzan en el punto\((3,4)\). Por lo tanto, el punto\((3,4)\) debe satisfacer ambas ecuaciones. Vamos a revisar.

Figura\(\PageIndex{1}\): El punto de intersección es una solución del sistema de ecuaciones lineales.

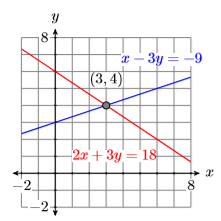
Sustituto\(3\) de\(x\) y\(4\) para\(y\).

\[\begin{aligned} x-3 y &=-9 \\ 3-3(4) &=-9 \\ 3-12 &=-9 \\-9 &=-9 \end{aligned} \nonumber \]

Sustituto\(3\) de\(x\) y\(4\) para\(y\).

\[\begin{aligned} 2 x+3 y &=18 \\ 2(3)+3(4) &=18 \\ 6+12 &=18 \\ 18 &=18 \end{aligned} \nonumber \]

De ahí que el punto\((3,4)\) satisfaga ambas ecuaciones y se le denomina solución del sistema.

Solución de un sistema lineal

Un punto\((x,y)\) se llama solución de un sistema de dos ecuaciones lineales si y solo si satisfacía ambas ecuaciones. Además, debido a que un punto satisface una ecuación si y solo si se encuentra en la gráfica de la ecuación, para resolver gráficamente un sistema de ecuaciones lineales, necesitamos determinar el punto de intersección de las dos líneas que tienen las ecuaciones dadas.

Probemos un ejemplo.

Ejemplo\(\PageIndex{1}\)

Resuelve el siguiente sistema de ecuaciones:\[3x+2y =12 \\ y =x+1 \label{system1}\]

Solución

Estamos buscando el punto\((x,y)\) que satisfaga ambas ecuaciones; es decir, estamos buscando el punto que se encuentra en la gráfica de ambas ecuaciones. Por lo tanto, el enfoque lógico es trazar las gráficas de ambas líneas, luego identificar el punto de intersección.

Primero, determinemos las\(x\) - y\(y\) -intercepciones de\(3x +2y = 12\).

Para encontrar la\(x\) -intercepción, vamos\(y = 0\).

\[\begin{aligned} 3 x+2 y &=12 \\ 3 x+2(0) &=12 \\ 3 x &=12 \\ x &=4 \end{aligned} \nonumber \]

Para encontrar la\(y\) -intercepción, vamos\(x = 0\).

\[\begin{aligned} 3 x+2 y &=12 \\ 3(0)+2 y &=12 \\ 2 y &=12 \\ y &=6 \end{aligned} \nonumber \]

De ahí que la\(x\) -intercepción es\((4,0)\) y la\(y\) -intercepción es\((0,6)\). Estas intercepciones se trazan en la Figura\(\PageIndex{2}\) y la línea\(3x +2y = 12\) se dibuja a través de ellas.

Figura\(\PageIndex{2}\): Dibujando la gráfica de\(3x +2y = 12\).

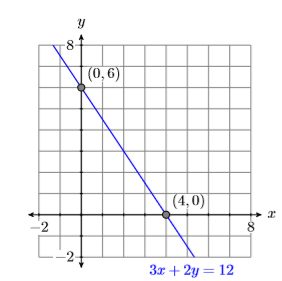
Comparando la segunda ecuación\(y = x + 1\) con la forma pendiente-intersección\(y = mx + b\), vemos que la pendiente es\(m = 1\) y ellos-intercepción es\((0,1)\). Traza la intercepción\((0,1)\), luego sube\(1\) unidad y\(1\) unidad derecha, luego dibuja la línea (ver Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Dibujando la gráfica de\(y = x + 1\).

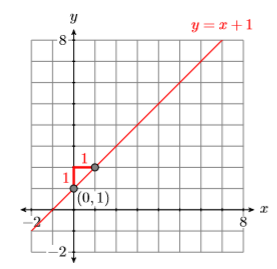
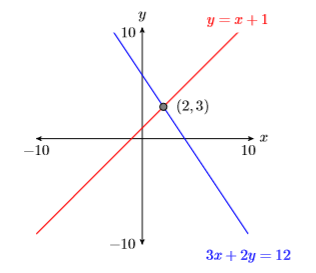
Estamos tratando de encontrar el punto que yace en ambas líneas, así trazamos ambas líneas en un mismo sistema de coordenadas, etiquetando cada una con su ecuación (ver Figura\(\PageIndex{4}\)). Parece que las líneas se cruzan en el punto\((2,3)\), haciendo\((x,y) = (2 ,3)\) la solución de Sistema en Ejemplo\(\PageIndex{1}\) (ver Figura\(\PageIndex{4}\)).

Check: Para mostrar que\((x,y) = (2 ,3)\) es una solución de System\ ref {system1}, debemos demostrar que obtenemos declaraciones verdaderas cuando sustituimos\(2\) por\(x\) y\(3\) para\(y\) en ambas ecuaciones de System\ ref {system1}.

Figura\(\PageIndex{4}\): Las coordenadas del punto de intersección es la solución de System\ ref {system1}.

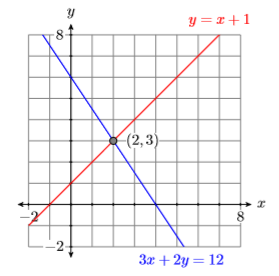
Sustituyendo\(2\) por\(x\) y\(3\) para\(y\) en\(3x +2y = 12\), obtenemos:

\[\begin{aligned} 3 x+2 y &=12 \\ 3(2)+2(3) &=12 \\ 6+6 &=12 \\ 12 &=12 \end{aligned} \nonumber \]

De ahí,\((2,3)\) satisface la ecuación\(3x +2y = 12\).

Sustituyendo\(2\) por\(x\) y\(3\) para\(y\) en\(y = x + 1\), obtenemos:

\[\begin{array}{l}{y=x+1} \\ {3=2+1} \\ {3=3}\end{array} \nonumber \]

De ahí,\((2,3)\) satisface la ecuación\(y = x + 1\).

Debido a\((2,3)\) que satisface ambas ecuaciones, esto hace\((2,3)\) una solución de System\ ref {system1}.

Ejercicio\(\PageIndex{1}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned} 2 x-5 y &=-10 \\ y &=x-1 \end{aligned} \nonumber \]

Contestar

\((5,4)\)

Ejemplo\(\PageIndex{2}\)

Resuelve el siguiente sistema de ecuaciones:\[3x-5y =-15 \\ 2x+y =-4 \label{system2}\]

Solución

Una vez más, estamos buscando el punto que satisfaga ambas ecuaciones del Sistema\ ref {system2}. Así, necesitamos encontrar el punto que se encuentra en las gráficas de ambas líneas representadas por las ecuaciones de System\ ref {system2}. El enfoque será graficar ambas líneas, luego aproximar las coordenadas del punto de intersección. Primero, determinemos las\(x\) - y\(y\) -intercepciones de\(3x−5y = −15\).

Para encontrar la\(x\) -intercepción, vamos\(y = 0\).

\[\begin{aligned} 3 x-5 y &=-15 \\ 3 x-5(0) &=-15 \\ 3 x &=-15 \\ x &=-5 \end{aligned} \nonumber \]

Para encontrar la\(y\) -intercepción, vamos\(x=0\).

\[\begin{aligned} 3 x-5 y &=-15 \\ 3(0)-5 y &=-15 \\-5 y &=-15 \\ y &=3 \end{aligned} \nonumber \]

De ahí que la\(x\) -intercepción es\((−5,0)\) y la\(y\) -intercepción es\((0,3)\). Estas intercepciones se trazan en la Figura\(\PageIndex{5}\) y la línea\(3x−5y = −15\) se dibuja a través de ellas.

Figura\(\PageIndex{5}\): Dibujando la gráfica de la línea\(3x−5y =−15\).

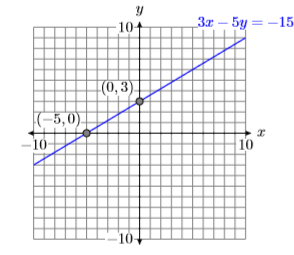
A continuación, determinemos las intercepciones de la segunda ecuación\(2x + y = −4\).

Para encontrar la\(x\) -intercepción, vamos\(y = 0\).

\[\begin{aligned} 2 x+y &=-4 \\ 2 x+0 &=-4 \\ 2 x &=-4 \\ x &=-2 \end{aligned} \nonumber \]

Para encontrar la\(y\) -intercepción, vamos\(x = 0\).

\[ \begin{aligned} 2 x+y &=-4 \\ 2(0)+y &=-4 \\ y &=-4 \end{aligned} \nonumber \]

De ahí que la\(x\) -intercepción es\((−2,0)\) y la\(y\) -intercepción es\((0,−4)\). Estas intercepciones se trazan en la Figura\(\PageIndex{6}\) y la línea\(2x + y =−4\) se dibuja a través de ellas.

Figura\(\PageIndex{6}\): Dibujando la gráfica de la línea\(2x + y = −4\).

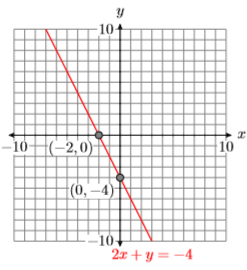
Para encontrar la solución de System\ ref {system2}, necesitamos trazar ambas líneas en un mismo sistema de coordenadas y determinar las coordenadas del punto de intersección. A diferencia de Ejemplo\(\PageIndex{1}\), en este caso tendremos que contentarnos con una aproximación de estas coordenadas. Parece que las coordenadas del punto de intersección son aproximadamente\((−2.6,1.4)\) (ver Figura\(\PageIndex{7}\)).

Comprobar: Debido a que solo tenemos una aproximación de la solución del sistema, no podemos esperar que la solución verifique exactamente en cada ecuación. No obstante, sí esperamos que la solución verifique aproximadamente.

Figura\(\PageIndex{7}\): Las coordenadas aproximadas del punto de intersección son\((−2.6,1.4)\).

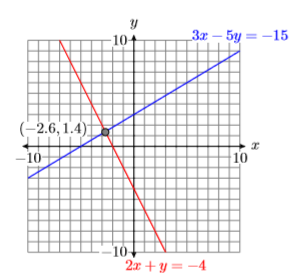
Sustituya\((x,y)=(−2.6,1.4)\) en la primera ecuación de System\ ref {system2}.

\[\begin{aligned} 3 x-5 y &=-15 \\ 3(-2.6)-5(1.4) &=-15 \\-7.8-7 &=-15 \\-14.8 &=-15 \end{aligned} \nonumber \]

Tenga en cuenta que\((x,y)=(−2.6,1.4)\) no comprueba exactamente, pero está bastante cerca de ser una declaración verdadera.

Sustituir\((x,y)=(−2.6,1.4)\) a la segunda ecuación de System\ ref {system2}.

\[\begin{aligned} 2 x+y=-4 \\ 2(-2.6)+1.4=-4 \\-5.2+1.4=-4 \\-3.8=-4 \end{aligned} \nonumber \]

Nuevamente, tenga en cuenta que\((x,y)= (−2.6,1.4)\) no comprueba exactamente, pero está bastante cerca de ser una afirmación verdadera.

Nota

Más adelante en esta sección aprenderemos a usar la utilidad de intersección en la calculadora gráfica para obtener una aproximación mucho más precisa de la solución real. Luego, en la Sección 4.2 y la Sección 4.3, mostraremos cómo encontrar la solución exacta.

Ejercicio\(\PageIndex{2}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned}-4 x-3 y &=12 \\ x-2 y &=-2 \end{aligned} \nonumber\]

Contestar

\((−2.7,−0.4)\)

Casos Excepcionales

La mayoría de las veces, dadas las gráficas de dos líneas, se cruzarán exactamente en un punto. Pero hay dos excepciones a este escenario general.

Ejemplo\(\PageIndex{3}\)

Resuelve el siguiente sistema de ecuaciones:\[2x+3y=6\\2x+3y=-6 \label{system3}\]

Solución

Coloquemos cada ecuación en forma de pendiente-intersección resolviendo cada ecuación para\(y\).

Resolver\(2x +3y = 6\) para\(y\):

\[\begin{aligned} 2 x+3 y &=6 \\ 2 x+3 y-2 x &=6-2 x \\ 3 y &=6-2 x \\ \dfrac{3 y}{3} &=\dfrac{6-2 x}{3} \\ y &=-\dfrac{2}{3} x+2 \end{aligned} \nonumber \]

Resolver\(2x +3y =−6\) para\(y\):

\[\begin{aligned} 2 x+3 y &=-6 \\ 2 x+3 y-2 x &=-6-2 x \\ 3 y &=-6-2 x \\ \dfrac{3 y}{3} &=\dfrac{-6-2 x}{3} \\ y &=-\dfrac{2}{3} x-2 \end{aligned} \nonumber \]

Comparando\(y =(−2/3)x+2\) con la forma pendiente-intersección nos\(y = mx+b\) dice que la pendiente es\(m = −2/3\) y ellos-intercepción es\((0,2)\). Traza la intercepción\((0,2)\), luego baja\(2\) unidades y unidades\(3\) derechas y dibuja la línea (ver Figura\(\PageIndex{8}\)).

Figura\(\PageIndex{8}\): Dibujando la gráfica de la línea\(2x +3y = 6\).

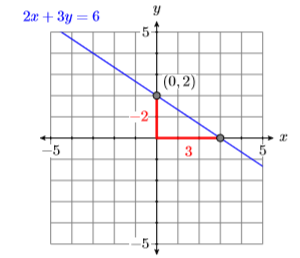
Comparando\(y =( −2/3)x − 2\) con la forma pendiente-intersección nos\(y = mx + b\) dice que la pendiente es\(m = −2/3\) y ellos-intercepción es\((0,−2)\). Traza la intercepción\((0 ,−2)\), luego baja\(2\) unidades y unidades\(3\) derechas y dibuja la línea (ver Figura\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): Dibujando la gráfica de la línea\(2x +3y =−6\).

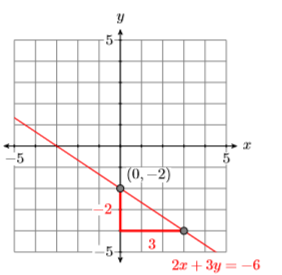
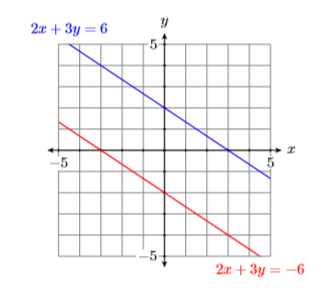
Para encontrar la solución de System\ ref {system3}, dibuje ambas líneas en el mismo sistema de coordenadas (ver Figura\(\PageIndex{10}\)). Observe cómo las líneas parecen ser paralelas (no se cruzan). El hecho de que ambas líneas tengan la misma pendiente\(−2/3\) confirece nuestra sospecha de que las líneas son paralelas. Sin embargo, tenga en cuenta que las líneas tienen diferentes\(y\) intercepciones. De ahí que estemos viendo dos líneas paralelas pero distintas (ver Figura\(\PageIndex{10}\)) que no se cruzan. De ahí que System\ ref {system3} no tenga solución.

Figura\(\PageIndex{10}\): Las líneas\(2x+3y = 6\) y\(2x+3y = −6\) son paralelas, líneas distintas.

Ejercicio\(\PageIndex{3}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned} x-y &=3 \\-2 x+2 y &=4 \end{aligned} \nonumber \]

Contestar

Sin solución.

Ejemplo\(\PageIndex{4}\)

Resuelve el siguiente sistema de ecuaciones:\[x-y=3 \\-2 x+2 y=-6 \label{system4}\]

Solución

Resolvamos ambas ecuaciones para\(y\).

Resolver\(x−y = 3\) para\(y\):

\[\begin{aligned} x-y &=3 \\ x-y-x &=3-x \\-y &=-x+3 \\-1(-y) &=-1(-x+3) \\ y &=x-3 \end{aligned} \nonumber \]

Resolver\(−2x +2y =−6\) para\(y\):

\[\begin{aligned}-2 x+2 y &=-6 \\-2 x+2 y+2 x &=-6+2 x \\ 2 y &=2 x-6 \\ \dfrac{2 y}{2} &=\dfrac{2 x-6}{2} \\ y &=x-3 \end{aligned} \nonumber \]

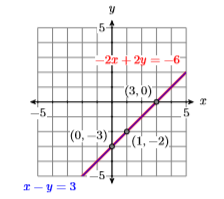
Ambas líneas tienen pendiente\(m = 1\), y ambas tienen la misma\(y\) -intercepción\((0,−3)\). De ahí que las dos líneas sean idénticas (ver Figura\(\PageIndex{11}\)). De ahí que System\ ref {system4} tenga un número infinito de puntos de intersección. Cualquier punto en cualquiera de las líneas es una solución del sistema. Ejemplos de puntos de intersección (soluciones que satisfacen ambas ecuaciones) son\((0,−3)\),\((1,−2)\), y\((3,0)\).

Figura\(\PageIndex{11}\): \(x − y = 3\)y\(−2x +2y = −6\) son la misma línea.

Solución alternativa:

Un enfoque mucho más fácil es señalar que si dividimos ambos lados de la segunda ecuación\(−2x +2y = −6\) por\(−2\), obtenemos:

\[\begin{aligned} -2x+2y &= -6 \quad {\color {Red} \text { Second equation in System }} \ref{system4}. \\ \dfrac{-2 x+2 y}{-2} &= \dfrac{-6}{-2} \quad \color {Red} \text { Divide both sides by }-2 \\ \dfrac{-2 x}{-2}+\dfrac{2 y}{-2} &= \dfrac{-6}{-2} \quad \color {Red} \text { Distribute }-2 \\ x-y &= 3 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

De ahí que la segunda ecuación en System\ ref {system4} sea idéntica a la primera. Por lo tanto, hay un número infinito de soluciones. Cualquier punto en cualquiera de las líneas es una solución.

Ejercicio\(\PageIndex{4}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned}-6 x+3 y &=-12 \\ 2 x-y &=4 \end{aligned} \nonumber \]

Contestar

Hay una cantidad infinita de soluciones. Las líneas son idénticas, por lo que cualquier punto en cualquiera de las dos líneas es una solución.

Ejemplos\(\PageIndex{1}\),\(\PageIndex{2}\),\(\PageIndex{3}\), y nos\(\PageIndex{4}\) llevan a la siguiente conclusión.

Número de soluciones de un sistema lineal

Cuando se trata de un sistema de dos ecuaciones lineales en dos incógnitas, solo hay tres posibilidades:

1. Exactamente hay una solución.
2. No hay soluciones.
3. Hay una cantidad infinita de soluciones.

Resolver sistemas con la calculadora gráfica

Ya hemos tenido experiencia graficando ecuaciones con la calculadora gráfica. También hemos utilizado el botón TRACE para estimar puntos de intersección. Sin embargo, la calculadora gráfica tiene una herramienta mucho más sofisticada para encontrar puntos de intersección. En el siguiente ejemplo usaremos la calculadora gráfica para encontrar la solución de System\ ref {system1} de Example\(\PageIndex{1}\).

Ejemplo\(\PageIndex{5}\)

Utilice la calculadora gráfica para resolver el siguiente sistema de ecuaciones:\[3x+2y=12 \\ y=x+1 \label{system5} \]

Solución

Para ingresar una ecuación en el menú Y=, la ecuación debe resolverse primero para\(y\). De ahí que primero debemos resolver\(3x +2y = 12\) para\(y\).

\[\begin{aligned} 3x+2y &=12 \quad \color {Red} \text { Original equation. } \\ 2y &= 12-3x \quad \color {Red} \text { Subtract } 3x \text { from both sides of the equation. } \\ \dfrac{2y}{2} &= \dfrac{12-3 x}{2} \quad \color {Red} \text { Divide both sides by } 2 \\ y &= \dfrac{12}{2}-\dfrac{3 x}{2} \quad \color {Red} \text { On the left, simplify. On the right, } \\ y &= 6-\dfrac{3}{2} x \quad \color {Red} \text { Simplify. } \end{aligned}\]

Ahora podemos sustituir ambas ecuaciones de System\ ref {system5} en el menú Y= (ver Figura\(\PageIndex{12}\)).

Figura\(\PageIndex{12}\): Ingresa ecuaciones de System\ ref {system5} en el menú Y=.

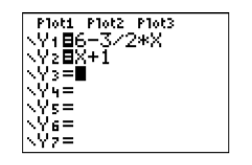
Seleccione 6:ZStandard en el menú ZOOM para producir las gráficas que se muestran en la Figura\(\PageIndex{13}\).

Figura\(\PageIndex{13}\): Seleccione 6:ZStandard para producir las gráficas de las ecuaciones System\ ref {system5}.

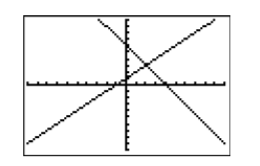
La pregunta ahora se convierte en “¿Cómo calculamos las coordenadas del punto de intersección?” Mire en su caja de calculadora justo encima del botón TRACE en la fila superior de botones, donde verá la palabra CalC, pintada en el mismo color que la tecla 2ND. Presiona la tecla 2ND, luego el botón TRACE, que abrirá el menú CALCULAR que se muestra en la Figura\(\PageIndex{14}\).

Figura\(\PageIndex{14}\): Presione 2ND, luego TRAZAR para abrir el menú CALCULAR. Después seleccione 5:intersectar para producir la pantalla en la Figura\(\PageIndex{15}\).

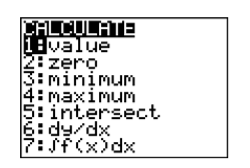
Nota

Hacer que la calculadora pregunte “Primera curva”, “Segunda curva”, cuando solo hay dos curvas en la pantalla puede parecer molesto. No obstante, imagina la situación cuando hay tres o más curvas en la pantalla. Entonces estas preguntas tienen buen sentido. Puede cambiar su selección de “Primera curva” o “Segunda curva” usando las teclas de flecha arriba y abajo para mover el cursor a una curva diferente.

Seleccione 5:intersectar. El resultado se muestra en la Figura\(\PageIndex{15}\). La calculadora ha colocado el cursor sobre la curva\(y =6−(3/2)x\) (vea la esquina superior izquierda de su pantalla de visualización), y en la esquina inferior izquierda la calculadora le pregunta si desea utilizar la curva seleccionada como la “Primera curva”. Responde “sí” presionando el botón ENTRAR.

Figura\(\PageIndex{15}\): Presiona la tecla ENTRAR en tu calculadora para decir “sí” a la selección de “Primera curva”.

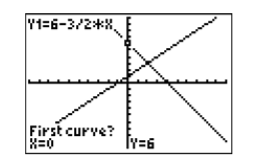
La calculadora responde como se muestra en la Figura\(\PageIndex{16}\). El cursor salta a la curva\(y = x + 1\) (ver esquina superior izquierda de tu ventana de visualización), y en la esquina inferior izquierda la calculadora te pregunta si quieres usar la curva seleccionada como la “Segunda curva”. Responde “sí” presionando de nuevo la tecla ENTRAR.

Figura\(\PageIndex{16}\): Presiona la tecla ENTRAR en tu calculadora para decir “sí” a la selección de “Segunda curva”.

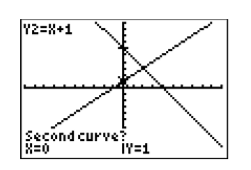
La calculadora responde como se muestra en la Figura\(\PageIndex{17}\), pidiéndole que “Adivina”. En este caso, deje el cursor donde está y presione nuevamente la tecla ENTER para señalar a la calculadora que está haciendo una suposición en la posición actual del cursor.

Figura\(\PageIndex{17}\): Presione la tecla ENTER para señalar a la calculadora que está satisfified con la posición actual del cursor como su suposición.

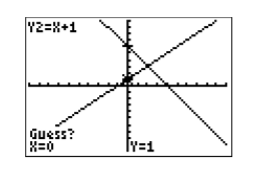
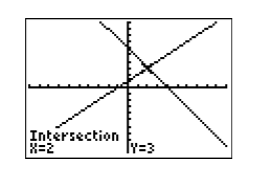
El resultado de presionar ENTRAR a la pregunta “Adivina” en la Figura\(\PageIndex{17}\) se muestra en la Figura\(\PageIndex{18}\), donde la calculadora ahora proporciona una aproximación de las coordenadas del punto de intersección en el borde inferior de la ventana de visualización. Tenga en cuenta que la calculadora ha colocado el cursor sobre el punto de intersección en la Figura\(\PageIndex{17}\) e informa que las coordenadas aproximadas del punto de intersección son\((2,3)\).

Figura\(\PageIndex{18}\): Lea las coordenadas aproximadas del punto de intersección a lo largo del borde inferior de la ventana de visualización.

Nota

En secciones posteriores, cuando investiguemos la intersección de dos gráficas que tienen más de un punto de intersección, las conjeturas serán más importantes. En esos casos futuros, necesitaremos usar las teclas de flecha izquierda y derecha para mover el cursor cerca del punto de intersección que deseamos que encuentre la calculadora.

Reportando tu solución en tu tarea. Al informar su solución en su trabajo de tarea, siga las Directrices para el envío de la calculadora del Capítulo 3, Sección 2. Haga una copia exacta de la imagen que se muestra en su ventana de visualización. Etiquete sus ejes\(x\) y\(y\). Al final de cada eje, ponga el valor apropiado de\(\mathrm{Xmin}, \mathrm{Xmax}, \mathrm{Ymin}\), y\(\mathrm{Ymax}\) reportado en el menú VENTANA de su calculadora. Usa una regla para dibujar las líneas y etiquetar cada una con sus ecuaciones. Finalmente, etiquetar el punto de intersección con sus coordenadas (ver Figura\(\PageIndex{19}\)). A menos que se indique lo contrario, siempre informe cada dígito que se muestre en su calculadora

Figura\(\PageIndex{19}\): Reportando tu resultado en tu trabajo de tarea.

Ejercicio\(\PageIndex{5}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned} 2 x-5 y &=9 \\ y &=2 x-5 \end{aligned} \nonumber \]

Contestar

\((2,-1)\)

En ocasiones necesitarás ajustar los parámetros en el menú VENTANA para que el punto de intersección sea visible en la ventana de visualización.

Ejemplo\(\PageIndex{6}\)

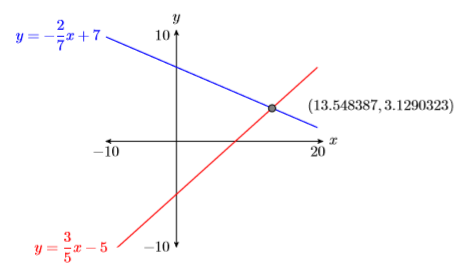
Utilice la calculadora gráfica para encontrar una solución aproximada del siguiente sistema:\[y=-\dfrac{2}{7} x+7\\ y=\dfrac{3}{5} x-5 \label{system6} \]

Solución

Cada ecuación de System\ ref {system6} ya está resuelta para\(y\), por lo que podemos proceder directamente e ingresarlas en el menú Y=, como se muestra en la Figura\(\PageIndex{20}\). Seleccione 6:ZStandard en el menú ZOOM para producir la imagen que se muestra en la Figura\(\PageIndex{21}\).

Figura\(\PageIndex{20}\): Ingresa las ecuaciones de System\ ref {system6}.

Figura\(\PageIndex{21}\): Seleccione 6:ZStandard para producir esta ventana.

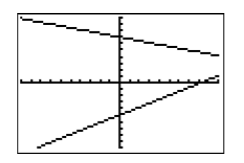
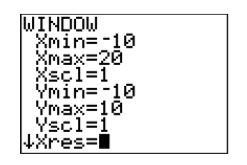
Obviamente, el punto de intersección está en la pantalla de la derecha, por lo que tendremos que aumentar el valor de\(\mathrm{Xmax}\) (set\(\mathrm{Xmax}=20\)) como se muestra en la Figura\(\PageIndex{22}\). Una vez que haya realizado ese cambio a\(\mathrm{Xmax}\), presione el botón GRAPAR para producir la imagen que se muestra en la Figura\(\PageIndex{23}\).

Figura\(\PageIndex{22}\): Cambiar\(\mathrm{Xmax}\) a\(20\).

Figura\(\PageIndex{23}\): Pulse el botón GRAPAR para producir esta ventana.

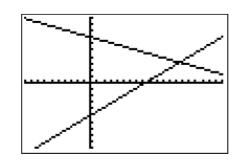
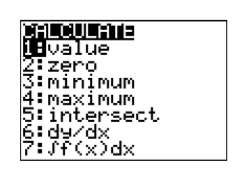
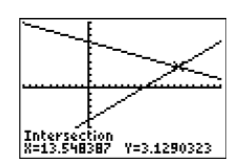
Ahora que el punto de intersección es visible en la ventana de visualización, presione 2ND CALC y seleccione 5:intersectar en el menú CALCULAR (ver Figura\(\PageIndex{24}\)). Haga tres pulsaciones consecutivas del botón ENTRAR para responder a “Primera curva”, “Segunda curva” y “Adivina”. La calculadora responde con la imagen de la Figura\(\PageIndex{25}\). Así, la solución de System\ ref {system6} es aproximadamente\((x,y) ≈ (13.54837,3.1290323)\).

Figura\(\PageIndex{24}\): Presione 2ND CALC para abrir el menú CALCULAR. Seleccione 5:intersectar para encontrar el punto de intersección.

Figura\(\PageIndex{25}\): Tres pulsaciones consecutivas de la tecla ENTER producen las coordenadas que se muestran en la parte inferior de la ventana de visualización.

\(\color {Red}Warning!\)

Su calculadora es una máquina de aproximación. Es muy probable que sus soluciones puedan variar ligeramente de la solución presentada en Figura\(\PageIndex{25}\) en los últimos\(2-3\) lugares.

Reportando tu solución en tu tarea:

Al informar su solución en su trabajo de tarea, siga las Directrices para el envío de la calculadora del Capítulo 3, Sección 2. Haga una copia exacta de la imagen que se muestra en su ventana de visualización. Etiquete sus ejes\(x\) y\(y\). Al final de cada eje, ponga el valor apropiado de\(\mathrm{Xmin}, \mathrm{Xmax}, \mathrm{Ymin}\), y\(\mathrm{Ymax}\) reportado en el menú VENTANA de su calculadora. Usa una regla para dibujar las líneas y etiquetar cada una con sus ecuaciones. Finalmente, etiquetar el punto de intersección con sus coordenadas (ver Figura\(\PageIndex{26}\)). A menos que se indique lo contrario, siempre informe cada dígito que se muestre en su calculadora

Figura\(\PageIndex{26}\): Reportando tu resultado en tu trabajo de tarea.

Ejercicio\(\PageIndex{6}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned} y &= \dfrac{3}{2} x+6 \\ y &= -\dfrac{6}{7} x-4\end{aligned} \nonumber \]

Contestar

\((-4.2,-0.4)\)