4.3: Resolver sistemas por eliminación

Cuando ambas ecuaciones de un sistema están en forma estándar\(Ax + By = C\), entonces un proceso llamado eliminación suele ser el mejor procedimiento para encontrar la solución del sistema. La eliminación se basa en dos ideas simples, la primera de las cuales debería ser familiar.

1. Multiplicar ambos lados de una ecuación por un número distinto de cero no cambia sus soluciones. Así, la ecuación\[x+3 y=7 \label{Eq4.3.1}\] tendrá las mismas soluciones (es la misma línea) que la ecuación obtenida multiplicando la Ecuación\ ref {Eq4.3.1} por\(2\):\[2 x+6 y=14 \]
2. Agregar dos ecuaciones verdaderas produce otra ecuación verdadera. Por ejemplo, considera lo que sucede cuando agregas\(4 = 4\) a\(5 = 5\). \[\begin{aligned} 4 &=4 \\ 5 &=5 \\ \hline 9 &=9 \end{aligned} \nonumber\]

Aún más importante, considera lo que sucede cuando agregas dos ecuaciones que tienen\((2,1)\) como solución. El resultado es una tercera ecuación cuya gráfica también pasa por la solución.

\[\begin{array}{rlrl}{x+y} & {=} & {3} \\ {x-y} & {=} & {1} \\ \hline 2 x\;\;\;\;\; & {=} & {4} \\ {x} \;\;\;\;\;& {=} & {2}\end{array} \nonumber \]

Figura\(\PageIndex{1}\)

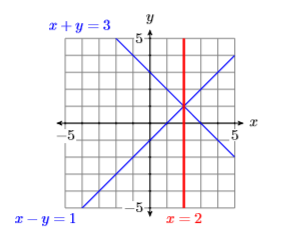
hecho

Agregar un múltiplo de una ecuación a una segunda ecuación produce una ecuación que pasa a través de la misma solución que las dos primeras ecuaciones.

Una cosa más importante a notar es el hecho de que cuando agregamos las ecuaciones\[\begin{aligned} x+y &=3 \\ x-y &=1 \\ \hline 2 x \;\;\;\;\;&=4 \end{aligned} \nonumber \]

se\(y\) eliminó la variable. Aquí es donde el método de eliminación recibe su nombre. La estrategia es agregar de alguna manera las ecuaciones de un sistema con la intención de eliminar una de las variables desconocidas. Sin embargo, a veces hay que hacer un poco más que simplemente agregar las ecuaciones. Veamos un ejemplo.

Ejemplo\(\PageIndex{1}\)

Resuelve el siguiente sistema de ecuaciones:

\[x+2y=-5 \label{Eq4.3.3} \]

\[2x-y=-5 \label{Eq4.3.4} \]

Solución

Nuestro enfoque será eliminar la variable\(x\). Tenga en cuenta que si multiplicamos la Ecuación\ ref {Eq4.3.3} por\(−2\), luego agregamos el resultado a la Ecuación\ ref {Eq4.3.4}, los\(x\) términos serán eliminados.

\[\begin{aligned}-2 x-4 y &=10 \quad {\color{Red} \text{Multiply equation}} \ref{Eq4.3.3} \color{Red} \text{ by } -2\\ 2 x-y &=-5 \quad {\color{Red} \text{Multiply equation}} \ref{Eq4.3.4}\\ \hline-5 y &=5 \quad \color{Red} \text {Add the equations.} \end{aligned} \nonumber \]

Divide ambos lados de\(−5y = 5\) por\(−5\) para obtener\(y =−1\). Para encontrar el valor correspondiente de\(x\), sustituir\(−1\)\(y\) en la Ecuación\ ref {Eq4.3.3} (o Ecuación\ ref {Eq4.3.4}) y resolver para\(x\).

\[\begin{aligned} x+2y &= -5 \quad {\color{Red} \text { Equation }} \ref{Eq4.3.3} \\ x+2(-1) &= -5 \quad \color{Red} \text { Substitute }-1 \text { for } y \\ x &= -3 \quad \color{Red} \text { Solve for } x . \end{aligned} \nonumber \]

Comprobar: Para verificar, necesitamos demostrar que el punto\((x,y)=( −3,1)\) satisface ambas ecuaciones.

Sustituir\((x,y)=( −3,−1)\) en Ecuación\ ref {Eq4.3.3}.

\[\begin{aligned} x+2 y &=-5 \\-3+2(-1) &=-5 \\-5 &=-5 \end{aligned} \nonumber \]

Sustituir\((x,y)=( −3,−1)\) IntoEquation\ ref {Eq4.3.4}.

\[\begin{aligned} 2 x-y &=-5 \\ 2(-3)-(-1) &=-5 \\-5 &=-5 \end{aligned} \nonumber \]

Así, el punto\((x,y)=(−3,−1)\) satisface ambas ecuaciones y por lo tanto es la solución del sistema.

Figura\(\PageIndex{2}\):\(x +2 y = −5\) y se\(2 x−y = −5\) cruzan en\(( −3,−1)\).

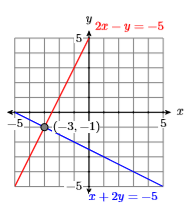
Ejercicio\(\PageIndex{1}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned} x+3 y &=14 \\-8 x-3 y &=-28 \end{aligned} \nonumber \]

Contestar

\((2,4)\)

Para demostrar que tienes la opción de qué variable eliges eliminar, probemos Ejemplo por\(\PageIndex{1}\) segunda vez, esta vez eliminando\(y\) en lugar de\(x\).

Ejemplo\(\PageIndex{2}\)

Resuelve el siguiente sistema de ecuaciones:

\[x+2y=-5 \label{Eq4.3.5} \]

\[2x-y=-5 \label{Eq4.3.6} \]

Solución

Esta vez nos enfocamos en eliminar la variable\(y\). Observamos que si multiplicamos la Ecuación\ ref {Eq4.3.6} por\(2\), luego agregamos el resultado a la Ecuación\ ref {Eq4.3.5}, los\(y\) términos serán eliminados.

\[\begin{aligned} x+2y &=-5 \quad {\color {Red} \text {Equation }} \ref{Eq4.3.5}\\ 4 x-2y &=-10 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.6} \color {Red} \text { by } 2\\ \hline 5x \;\;\;\;\;\;\;&=-15 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]

Divide ambos lados de\(5x = −15\) por\(5\) para obtener\(x =−3\). Para encontrar el valor correspondiente de\(y\), sustituir\(−3\)\(x\) en Ecuación\ ref {Eq4.3.5} (o Ecuación\ ref {Eq4.3.6}) y resolver para\(y\).

\[\begin{aligned} x+2y &= -5 \quad {\color {Red} \text { Equation }} \ref{Eq4.3.5} \\ -3+2y &= -5 \quad \color {Red} \text { Substitute }-3 \text { for } x \\ 2y &= -2 \quad \color {Red} \text { Add } 3 \text { to both sides. } \\ y &= -1 \quad \color {Red} \text { Divide both sides by } 2 \end{aligned} \nonumber \]

De ahí que\((x,y)=(−3,−1)\), al igual que en Ejemplo\(\PageIndex{1}\), es la solución del sistema.

Figura\(\PageIndex{3}\): \(x +2 y = −5\)y se\(2 x−y = −5\) cruzan en\(( −3,−1)\).

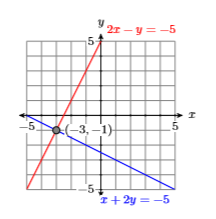
A veces la eliminación requiere un proceso de pensamiento similar al de encontrar un denominador común.

Ejemplo\(\PageIndex{3}\)

Resuelve el siguiente sistema de ecuaciones:

\[3x+4y=12 \label{Eq4.3.7} \]

\[2x-5y=10 \label{Eq4.3.8} \]

Solución

Centrémonos en eliminar los\(x\) términos. Tenga en cuenta que si multiplicamos la Ecuación\ ref {Eq4.3.7} por\(2\), luego multiplicamos la Ecuación\ ref {Eq4.3.8} por\(−3\), los\(x\) -términos serán eliminados cuando sumemos las ecuaciones resultantes.

\[\begin{aligned} 6x+8y &= 24 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.7} \color {Red} \text { by } 2\\ -6x+15y &= -30 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.8} \color {Red} \text { by } 2\\ \hline 23y &= -6 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]

De ahí,\(y = −6/23\).

En este punto, podríamos sustituir\(y = −6/23\) en cualquiera de las ecuaciones, luego resolver el resultado para\(x\). Sin embargo, trabajar con\(y = −6/23\) él es un poco desalentador, particularmente a la luz de que la eliminación es más fácil. Entonces usemos de nuevo la eliminación, esta vez enfocándonos en eliminar\(y\). Tenga en cuenta que si multiplicamos la Ecuación\ ref {Eq4.3.7} por\(5\), luego multiplicamos la Ecuación\ ref {Eq4.3.8} por\(4\), cuando sumamos los resultados, los\(y\) -términos serán eliminados.

\[\begin{aligned} 5x+20y &= 60 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.7} \color {Red} \text { by } 5\\ 8x-20y &= 40 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.8} \color {Red} \text { by } 4\\ \hline 23x\;\;\;\;\;\;\;\;\; &= 100 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]

Así,\(x = 100/23\), y el sistema del sistema es\((x,y) = (100/23,−6/23)\).

Figura\(\PageIndex{4}\):\(3x +4 y = 12\) y se\(2x−5y = 10\) cruzan en\((100/23,−6/23)\).

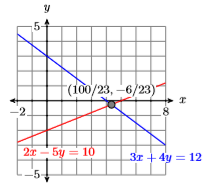
Consulta: Vamos a usar la calculadora gráfica para verificar la solución. Primero, almacene\(100/23\) en\(X\), luego\(−6/23\) en\(Y\) (ver Figura\(\PageIndex{5}\)). A continuación, ingresa los lados izquierdos de las ecuaciones\ ref {Eq4.3.7} y\ ref {Eq4.3.8}.

Figura\(\PageIndex{5}\): Entrar\(100/23\) en\(X\),\(−6/23\) en\(Y\).

Figura\(\PageIndex{6}\): Ingresa los lados izquierdos de las ecuaciones\ ref {Eq4.3.7} y\ ref {Eq4.3.8}.

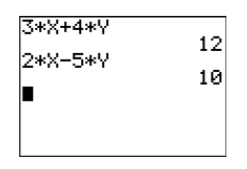
Tenga en cuenta que ambos cálculos en la Figura\(\PageIndex{6}\) proporcionan los lados correctos a la derecha para las ecuaciones\ ref {Eq4.3.7} y\ ref {Eq4.3.8}. Así, la solución\((x,y) = (100/23,−6/23)\) comprueba.

Ejercicio\(\PageIndex{3}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned}-14 x+9 y &=94 \\ 7 x+3 y &=-62 \end{aligned} \nonumber \]

Contestar

\((-8,-2)\)

Casos Excepcionales

En el apartado anterior, vimos que si el método de sustitución llevaba a una declaración falsa, entonces tenemos líneas paralelas. Lo mismo puede suceder con el método de eliminación de esta sección.

Ejemplo\(\PageIndex{4}\)

Resuelve el siguiente sistema de ecuaciones:

\[x+y=3 \label{Eq4.3.9} \]

\[2x+2y=6 \label{Eq4.3.10} \]

Solución

Centrémonos en eliminar los\(x\) términos. Tenga en cuenta que si multiplicamos la Ecuación\ ref {Eq4.3.9} por\(−2\), los\(x\) -términos serán eliminados cuando sumemos las ecuaciones resultantes.

\[\begin{aligned} -2x-2y &= -6 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.9} \color {Red} \text { by } -2\\ 2x+2y &= -6 \quad {\color {Red} \text {Equation }} \ref{Eq4.3.10} \\ \hline 0 &= -12 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]

Debido a nuestra experiencia con esto resolviendo este caso excepcional con sustitución, el hecho de que ambas variables hayan desaparecido no debería ser del todo sorprendente. Tenga en cuenta que esta última afirmación es falsa, independientemente de los valores de\(x\) y\(y\). De ahí que el sistema no tenga solución.

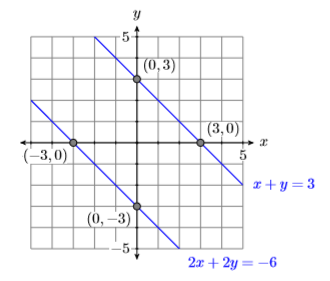
En efecto, si encontramos las intercepciones de cada ecuación y las trazamos, entonces podemos ver fácilmente que las líneas de este sistema son paralelas (ver Figura\(\PageIndex{7}\)). Las líneas paralelas nunca se cruzan, por lo que el sistema no tiene soluciones.

Figura\(\PageIndex{7}\): Las líneas\(x + y = 3\) y\(2x +2y = −6\) son paralelas.

Ejercicio\(\PageIndex{4}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{aligned} 5 x-4 y &=-16 \\ 15 x-12 y &=49 \end{aligned} \nonumber \]

Contestar

no hay solución

En el apartado anterior, vimos que si el método de sustitución llevaba a una afirmación verdadera, entonces tenemos las mismas líneas. Lo mismo puede suceder con el método de eliminación de esta sección.

Ejemplo\(\PageIndex{5}\)

Resuelve el siguiente sistema de ecuaciones:

\[x-7y=4 \label{Eq4.3.11} \]

\[-3x+21y=-12 \label{Eq4.3.12} \]

Solución

Si no estamos en piloto automático a altas horas de la noche haciendo nuestros deberes, podríamos reconocer que las ecuaciones\ ref {Eq4.3.11} y\ ref {Eq4.3.12} son idénticas. Pero también es concebible que no veamos eso de inmediato y comencemos el método de eliminación. Multipliquemos la primera ecuación por\(3\), luego sumemos. Esto eliminará los\(x\) -términos.

\[\begin{aligned} 3x-21y &= 12 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.11} \color {Red} \text { by } 3\\ 3x+21y &= -12 \quad {\color {Red} \text {Equation }} \ref{Eq4.3.12} \\ \hline 0 &= 0 \quad \color {Red} \text {Add the equations.} \end{aligned} \nonumber \]

De nuevo, ¡todas las variables han desaparecido! No obstante, esta vez la última afirmación es cierta, independientemente de los valores de\(x\) y\(y\).

Observe que si multiplicamos la Ecuación\ ref {Eq4.3.11} por\(−3\), entonces tenemos dos ecuaciones idénticas.

\[\begin{aligned} -3x+21y &= -12 \quad {\color {Red} \text {Multiple equation }} \ref{Eq4.3.11} \color {Red} \text { by } 3\\ -3x+21y &= -12 \quad {\color {Red} \text {Equation }} \ref{Eq4.3.12} \end{aligned} \nonumber \]

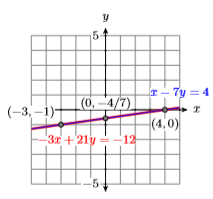
¡Las ecuaciones son idénticas! De ahí que haya un número infinito de puntos de intersección. En efecto, cualquier punto en cualquiera de las líneas es una solución. Ejemplos de puntos de solución son\((−3,−1)\),\((0,−4/7)\), y\((4,0)\).

Figura\(\PageIndex{8}\): \(x−7y = 4\)y\(−3x + 21 y = −12\) son la misma línea. Infinite número de soluciones.

Ejercicio\(\PageIndex{5}\)

Resuelve el siguiente sistema de ecuaciones:

\[\begin{array}{c}{2 x-7 y=4} \\ {8 x-28 y=16}\end{array} \nonumber \]

Contestar

Hay una cantidad infinita de soluciones. Ejemplos de puntos de solución son\((2,0)\),\((9,2)\), y\((−5,−2)\).