Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

6.6: Estrategia de Factoring

Última actualización

30 oct 2022
Guardar como PDF
- 6.5: Factorización de Formas Especiales
- 6.7: Aplicaciones de Factoring

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Cuando te estás concentrando en factorizar problemas de un solo tipo, después de hacer algunos tiendes a meterte en un ritmo, y el resto de los ejercicios, por ser similares, parecen flotar. Sin embargo, cuando te encuentras con una mezcla de problemas de factorización de diferentes tipos, el progreso es más difícil. El objetivo de esta sección es establecer una estrategia a seguir al atacar un problema general de factorización.

Si aún no se ha hecho, es útil organizar los términos del polinomio dado en algún tipo de orden (descendente o ascendente). Entonces quieres aplicar las siguientes pautas.

Estrategia de Factoring

Estos pasos deben seguirse en el orden en que aparezcan.

Factorizar el mayor factor común ( $\mathrm{GCF}$ ).
Busca una forma especial.
1. Si tienes dos cuadrados perfectos separados por un signo menos, usa el patrón de diferencias de cuadrados para factorizar: $a^2 −b^2 =(a + b)(a−b)\nonumber$
2. Si tienes un trinomio cuyo primer y último término son cuadrados perfectos, debes sospechar que tienes un trinomio cuadrado perfecto. Tomar las raíces cuadradas del primer y último término y factorizar de la siguiente manera. $a^2 +2ab + b^2 =(a + b)^2 \nonumber$ Asegúrese de verificar que el término medio sea correcto.
Si tienes un trinomio de la forma $ax^2 + bx + c$ , usa el $ac$ método -para factorizar.
Si tienes una expresión de cuatro términos, intenta factorizar agrupando.

Una vez que hayas aplicado la estrategia anterior al polinomio dado, es muy posible que uno de tus factores resultantes factorizará aún más. Así, tenemos la siguiente regla.

Factor completamente

El proceso de factorización no está completo hasta que ninguno de sus factores restantes pueda ser factorizado más. Este es el significado de la frase, “factor completamente”.

Por último, un muy buen consejo.

Comprueba tu factorización multiplicando

Una vez que hayas factorizado completamente el polinomio dado, es una muy buena práctica verificar tu resultado. Si multiplicas para encontrar el producto de tus factores, y obtienes como resultado el polinomio original dado, entonces sabes que tu factorización es correcta.

Es un poco más de trabajo verificar tu factorización, pero vale la pena el eort. Ayuda a eliminar errores y también ayuda a construir una mejor comprensión del proceso de factoring. Recuerde, el factoring es “no multiplicar”, así que cuanto más se multiplique, mejor se obtiene en el factoring.

¡Veamos qué puede pasar cuando no revisas tu factorización!

¡Advertencia! ¡La siguiente solución es incorrecta!

Factor: $2x^4 +8x^2$

Solución: factorizar el $\mathrm{GCF}$

$\begin{align*} 2x^4+8x^2 &= 2x^2(x^2+4) \\ &= 2x^2(x+2)^2 \end{align*} \nonumber$

Tenga en cuenta que este alumno no se molestó en revisar su factorización. Hagámoslo por él ahora.

Cheque: Multiplicar para verificar. Recuerda, al cuadrar un binomio, hay un término medio.

$\begin{align*} 2x^2(x+2)^2 &= 2x^2(x^2+4x+4) \\ &= 2x^4+8x^3+8x^2 \end{align*} \nonumber$

Esto no es lo mismo que el polinomio original $2x^4 +8x^2$ , por lo que la factorización del estudiante es incorrecta. Si el alumno hubiera realizado esta comprobación, podría haber captado su error, siempre y cuando por supuesto, se multiplique correctamente durante la comprobación.

Sigue la factorización correcta.

$\begin{align*} 2x^4+8x^2 &= 2x^2(x^2+4) \\ \end{align*} \nonumber$

La suma de cuadrados no factoriza, así que estamos finalizados.

Cheque: Multiplicar para verificar.

$\begin{align*} 2x^2(x^2+4) &= 2x^4+8x^2\\ \end{align*} \nonumber$

Esto es lo mismo que el polinomio original $2x^4 +8x^2$ , por lo que esta factorización es correcta.

Ejemplo $\PageIndex{1}$

Factor completamente: $−3x^6 +3x^2$

Solución

La primera regla de factorización es “Factorizar el GCF”. El $\mathrm{GCF}$ de $−3x^6$ y $3x^2$ es $3x^2$ , así podríamos factorizar $3x^2$ .

$−3x^6 +3x^2 =3x^2(−x^4 + 1) \nonumber$ Esto es perfectamente válido, pero no nos gusta que empiece con el segundo factor

$−x^4$ . Vamos a factorizar

$−3x^2$ en su lugar.

$−3x^6 +3x^2 = −3x^2(x^4 −1) \nonumber$ El segundo factor es la diferencia de dos cuadrados. Toma las raíces cuadradas, separando un par con un signo más, un par con un signo menos.

$= −3x^2(x^2 + 1)(x^2 −1) \nonumber$ La suma de cuadrados no factoriza. Pero el último factor es la diferencia de dos cuadrados. Toma las raíces cuadradas, separando un par con un signo más, un par con un signo menos.

$= −3x^2(x^2 + 1)(x + 1)(x−1) \nonumber$

Cheque: Multiplica para verificar el resultado.

$\begin{align*} -3x^2(x^2+1)(x+1)(x-1) &= -3x^2(x^2+1)(x^2-1)\\ &= -3x^2(x^4-1)\\ &= -3x^6+3x^2 \end{align*} \nonumber$

Las comprobaciones de factorización.

Ejercicio $\PageIndex{1}$

Factor completamente: $−4x^7 + 64x^3$

Contestar: $−4x^3(x^2 + 4)(x + 2)(x−2)$

Ejemplo $\PageIndex{2}$

Factor completamente: $x^3y +9xy^3 +6x^2y^2$

Solución

La primera regla de factorización es “Factorizar el GCF”. El $\mathrm{GCF}$ de $x^3y$ , $9xy^3$ , y $6x^2y^2$ es $xy$ , entonces factorizamos $xy$ .

$x^3y +9xy^3 +6x^2y^2 = xy(x^2 +9y^2 +6xy) \nonumber$ Ordenemos ese segundo factor en poderes descendentes de

$x$ .

$= xy(x^2 +6xy +9y^2) \nonumber$ El primer y último término del factor trinomial son cuadrados perfectos. Sospechamos que tenemos un trinomio cuadrado perfecto, así que tomamos las raíces cuadradas del primer y último término, verificamos el término medio, y escribimos:

$= xy(x +3y)^2 \nonumber$ Así,

$x^3y +9xy^3 +6x^2y^2 = xy(x +3y)^2$ .
Cheque: Multiplica para verificar el resultado.

$\begin{align*} xy(x+3y)^2 &= xy(x^2 +6xy +9y^2)\\ &= x^3y+6x^2y^2 +9xy^3 \end{align*} \nonumber$
Excepto por el orden, este resultado es el mismo que el polinomio dado. Las comprobaciones de factorización.

Ejercicio $\PageIndex{2}$

Factor completamente: $3a^2b^4 + 12a^4b^2 −12a^3b^3$

Contestar: $3a^2b^2(2a−b)^2$

Ejemplo $\PageIndex{3}$

Factor completamente: $2x^3 −48x + 20x^2$

Solución

En el último ejemplo, reconocimos la necesidad de reorganizar nuestros términos después de que sacamos el $\mathrm{GCF}$ . Esta vez, arreglemos nuestros términos en poderes descendentes de $x$ inmediato.

$2x^3 −48x + 20x^2 =2x^3 + 20x^2 −48x \nonumber$ Ahora, vamos a factorizar el

$\mathrm{GCF}$ .

$=2x(x^2 + 10x−24) \nonumber$ El último término del factor trinomio no es un cuadrado perfecto. Pasemos al método ac a factorizar. El par entero

$−2,12$ tiene un producto igual a

$ac = −24$ y una suma igual a

$b = 10$ . Debido a que el coeciente de

$x^2$ es uno, esta es una situación de “caída en el lugar”. Dejamos caer nuestro par en su lugar y escribimos:

$=2x(x−2)(x + 12) \nonumber$ Así,

$2x^3 −48x + 20x^2 =2x(x−2)(x + 12)$ .

Cheque: Multiplica para verificar el resultado. Utilizamos el método abreviado FOIL y cálculos mentales para acelerar las cosas.

$\begin{align*} 2x(x-2)(x + 12) &= 2x(x^2+10x-24) \\ &= 2x^3 + 20x^2 - 48x \end{align*} \nonumber$ Excepto por el orden, este resultado es el mismo que el polinomio dado. Las comprobaciones de factorización.

Ejercicio $\PageIndex{3}$

Agrega texto de ejercicios aquí.

Contestar: $−3x^2(x−4)(x−5)$

Ejemplo $\PageIndex{4}$

Factor completamente: $2a^2 −13ab−24b^2$

Solución

No hay un factor común que podamos factorizar. Tenemos un trinomio, pero el primer y último término no son cuadrados perfectos, así que vamos a aplicar el $ac$ método -. Ignorando las variables por un momento, necesitamos un par entero cuyo producto es $ac = −48$ y cuya suma es $−13$ . El par entero $3,−16$ viene a la mente (si nada viene a la mente, empieza a enumerar pares enteros). Dividir el término medio en una suma de términos similares usando el par entero $3,−16$ , luego factorizar agrupando

$\begin{align*} 2a^2-13ab-24b^2 &= 2a^2 +3ab-16ab-24b^2 \\ &= a(2a+3b)-8b(2a+3b)\\ &= (a-8b)(2a+3b) \end{align*} \nonumber$

Por lo tanto, $2a^2-13ab-24b^2 =( a−8b)(2a +3 b)$ .

Cheque: Multiplica para verificar el resultado. Utilizamos el método abreviado FOIL y cálculos mentales para acelerar las cosas.

$(a−8b)(2a +3 b)=2a^2 −13ab−24b^2 \nonumber$ Este resultado es el mismo que el polinomio dado. Las comprobaciones de factorización.

Ejercicio $\PageIndex{4}$

Factor completamente: $8x^2 + 14xy−15y^2$

Contestar: $(2 x +5y)(4x−3y)$

Ejemplo $\PageIndex{5}$

Factor completamente: $30x^4 + 38x^3 −20x^2$

Solución

El primer paso es factorizar el $\mathrm{GCF}$ , que en este caso lo es $2x^2$ .

$30x^4 + 38x^3 −20x^2 =2x^2(15x^2 + 19x−10) \nonumber$ El primer y último término del factor trinomio no son cuadrados perfectos, así que volvamos al

$ac$ método -. Comparando

$15x^2+19x−10$ con

$ax^2+bx+c$ , tenga en cuenta que

$ac = (15)(−10) = −150$ . Necesitamos un par entero cuyo producto es

$−150$ y cuya suma es

$19$ . El par entero

$−6$ y

$25$ satisface estos requisitos. Porque

$a \neq 1$ , esta no es una situación de “caída en el lugar”, por lo que necesitamos romper el término medio como una suma de términos similares usando el par

$−6$ y

$25$ .

$=2x^2(15x^2 −6x + 25x−10) \nonumber$ Factorizar por agrupación. Factor

$3x$ de los dos primeros términos y

$5$ del tercer y cuarto términos.

$=2x^2(3x(5x−2) + 5(5x−2)) \nonumber$ Finalmente, factorizar el factor común

$5x−2$ .

$=2x^2(3x + 5)(5x−2) \nonumber$ Así,

$30x^4 + 38x^3 −20x^2 =2x^2(3x + 5)(5x−2)$ .

Cheque: Multiplica para verificar el resultado. Usa el método FOIL para multiplicar primero los binomios.

$2x^2(3x + 5)(5x−2) = 2x^2(15x^2 + 19x−10) \nonumber$ Distribuir el

$2x^2$ .

$= 30x^4 + 38x^3 −20x^2 \nonumber$ Este resultado es el mismo que el polinomio dado. Las comprobaciones de factorización.

Ejercicio $\PageIndex{5}$

Factor completamente: $36x^3 + 60x^2 +9x$

Contestar: $3x(6x + 1)(2x + 3)$

Ejemplo $\PageIndex{6}$

Factor completamente: $8x^5 + 10x^4 −72x^3 −90x^2$

Solución

Cada uno de los términos es divisible por $3x^3$ . Factorizar hacia fuera $3x^3$ .

$15x^6 −33x^5 −240x^4 + 528x^3 =3x^3[5x^3 −11x^2 −80x + 176] \nonumber$ El segundo factor es una expresión de cuatro términos. Factorizar por agrupación.

$\begin{align*} &= 3x^3[x^2(5x-11)-16(5x-11)] \\ &= 3x^3(x^2-16)(5x-11) \end{align*} \nonumber$

El factor $x^2−16$ es una diferencia de dos cuadrados. Toma las raíces cuadradas, separa un par con un plus, un par con un menos.

$=3x^3(x + 4)(x−4)(5x−11) \nonumber$ Por lo tanto,

$15x^6 −33x^5 −240x^4 + 528x^3 =3x^3(x + 4)(x−4)(5x−11)$ .

Cheque: Multiplica para verificar el resultado.

$\begin{align*} 3x^3(x + 4)(x-4)(5x-11) &= 3x^3(x^2-16)(5x-11) \\ &= 3x^3(5x^3 - 11x^2 - 80x + 176 \\ &= 15x^6 - 33x^5 - 240x^4 + 528x^3 \end{align*} \nonumber$

Este resultado es el mismo que el polinomio dado. Las comprobaciones de factorización.

Ejercicio $\PageIndex{6}$

Factor completamente: $15x^6−33x^5−240x^4 +528x^3$

Contestar: $2x^2(x−3)(x + 3)(4x + 5)$

Uso de la Calculadora para Ayudar al $ac$ Método

Cuando se usa el $ac$ método -para factorizar $ax^2+bx+c$ y $ac$ es un número muy grande, entonces puede ser difícil encontrar un par cuyo producto es $ac$ y cuya suma en $b$ . Por ejemplo, considera el trinomio:

$12y^2 −11y−36 \nonumber$ Necesitamos un par entero cuyo producto es

$ac =−432$ y cuya suma es

$b = −11$ . Comenzamos a enumerar las posibilidades de pares enteros, pero el proceso rápidamente se vuelve desalentador.

$\begin{array}{l} 1,-432\\ 2,-216\\ \quad\dots \end{array} \nonumber$

Tenga en cuenta que los números en la segunda columna se encuentran dividiendo $ac =−432$ por el número en la primera columna. Ahora usaremos este hecho y la función TABLE en nuestra calculadora para buscar el par entero deseado.

Ingrese la expresión $-432/X$ en $\mathbb{Y1}$ en el menú Y= (vea la primera imagen en la Figura $\PageIndex{1}$ ).
Encima del botón VENTANA verás TBLSET. Use la tecla 2nd, luego presione el botón VENTANA para acceder al menú que se muestra en la segunda imagen de la Figura $\PageIndex{1}$ . Establezca tblStart=1 $\triangle \text {Tbl}=1$ , y luego resalte AUTO para las variables independientes y dependientes.
Encima del botón GRÁFICO verás TABLA. Use la tecla 2nd, luego presione el botón GRAPH para acceder a la tabla que se muestra en la tercera imagen de la Figura $\PageIndex{1}$ . Utilice las teclas de flecha arriba y abajo para desplazarse por el contenido de la tabla. Tenga en cuenta que puede ignorar la mayoría de los pares, porque no son ambos enteros. Presta atención sólo cuando ambos son enteros. En este caso, recuerda que estás buscando un par cuya suma sea $b = −11$ . Tenga en cuenta que el par que $16,−27$ se muestra en la tercera imagen de Figura $\PageIndex{1}$ es el par que buscamos.

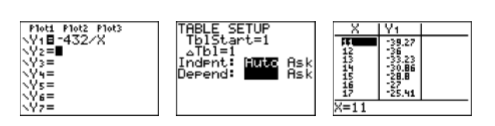
higo 6.6.1.png — Figura $\PageIndex{1}$ : Uso de la función **TABLE** para ayudar al $ac$ método.

Ahora podemos dividir el término medio de $12y^2 −11y −36$ en una suma de términos similares usando el par ordenado $16,−27$ , luego factorizar por agrupación.

$\begin{align*} 12y^2-11y-36 &= 12y^2 + 16y-27y-36\\ &= 4y(3y + 4)-9(3y + 4) \\ &= (4y-9)(3y+4) \end{align*} \nonumber$

Comprobar: Utilice el método abreviado FOIL y los cálculos mentales para multiplicar.

$(4y−9)(3y + 4) = 12y^2 −11y−36 \nonumber$ Las comprobaciones de factorización.

Uso de la Calculadora para Ayudar alacac Método

Support Center

How can we help?

Uso de la Calculadora para Ayudar al $ac$ Método