Saltar al contenido principal
LibreTexts Español

1.2E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    110418

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    Usar valor posicional con números enteros

    En los siguientes ejercicios, encuentra el valor posicional de cada dígito en los números dados.

    Ejercicio\(\PageIndex{34}\)

    51,493

    1. 1
    2. 4
    3. 9
    4. 5
    5. 3
    Contestar
    1. miles
    2. cientos
    3. decenas
    4. diez miles
    5. unos
    Ejercicio\(\PageIndex{35}\)

    87,210

    1. 2
    2. 8
    3. 0
    4. 7
    5. 1
    Ejercicio\(\PageIndex{36}\)

    164,285

    1. 5
    2. 6
    3. 1
    4. 8
    5. 2
    Contestar
    1. unos
    2. diez miles
    3. cien miles
    4. decenas
    5. cientos
    Ejercicio\(\PageIndex{37}\)

    395,076

    1. 5
    2. 3
    3. 7
    4. 0
    5. 9
    Ejercicio\(\PageIndex{38}\)

    93,285,170

    1. 9
    2. 8
    3. 7
    4. 5
    5. 3
    Contestar
    1. diez millones
    2. diez miles
    3. decenas
    4. miles
    5. millones
    Ejercicio\(\PageIndex{39}\)

    36,084,215

    1. 8
    2. 6
    3. 5
    4. 4
    5. 3
    Ejercicio\(\PageIndex{40}\)

    7,284,915,860,132

    1. 7
    2. 4
    3. 5
    4. 3
    5. 0
    Contestar
    1. trillones
    2. miles de millones
    3. millones
    4. decenas
    5. miles
    Ejercicio\(\PageIndex{41}\)

    2,850,361,159,433

    1. 9
    2. 8
    3. 6
    4. 4
    5. 2

    En los siguientes ejercicios, nombra cada número usando palabras.

    Ejercicio\(\PageIndex{42}\)

    1,078

    Contestar

    mil setenta y ocho

    Ejercicio\(\PageIndex{43}\)

    5,902

    Ejercicio\(\PageIndex{44}\)

    364,510

    Contestar

    trescientos sesenta y cuatro mil quinientos diez

    Ejercicio\(\PageIndex{45}\)

    146,023

    Ejercicio\(\PageIndex{46}\)

    5,846,103

    Contestar

    cinco millones ochocientos cuarenta y seis mil ciento tres

    Ejercicio\(\PageIndex{47}\)

    1,458,398

    Ejercicio\(\PageIndex{48}\)

    37,889,005

    Contestar

    treinta y siete millones ochocientos ochenta y nueve mil cinco

    Ejercicio\(\PageIndex{49}\)

    62,008,465

    En los siguientes ejercicios, escribe cada número como un número entero usando dígitos.

    Ejercicio\(\PageIndex{50}\)

    cuatrocientos doce

    Contestar

    412

    Ejercicio\(\PageIndex{51}\)

    doscientos cincuenta y tres

    Ejercicio\(\PageIndex{52}\)

    treinta y cinco mil novecientos setenta y cinco

    Contestar

    35,975

    Ejercicio\(\PageIndex{53}\)

    sesenta y uno mil cuatrocientos quince

    Ejercicio\(\PageIndex{54}\)

    once millones cuarenta y cuatro mil ciento sesenta y siete

    Contestar

    11,044,167

    Ejercicio\(\PageIndex{55}\)

    dieciocho millones, ciento dos mil setecientos ochenta y tres

    Ejercicio\(\PageIndex{56}\)

    tres mil millones, doscientos veintiséis millones, quinientos doce mil, diecisiete

    Contestar

    3,226,512,017

    Ejercicio\(\PageIndex{57}\)

    once mil millones, cuatrocientos setenta y un millones, treinta y seis mil, ciento seis

    En lo siguiente, redondear al valor posicional indicado.

    Ejercicio\(\PageIndex{58}\)

    Redondear al diez más cercano.

    1. 386
    2. 2,931
    Contestar
    1. 390
    2. 2,930
    Ejercicio\(\PageIndex{59}\)

    Redondear al diez más cercano.

    1. 792
    2. 5,647
    Ejercicio\(\PageIndex{60}\)

    Redondear al cien más cercano.

    1. 13,748
    2. 391,794
    Contestar
    1. 13,700
    2. 391,800
    Ejercicio\(\PageIndex{61}\)

    Redondear al cien más cercano.

    1. 28,166
    2. 481,628
    Ejercicio\(\PageIndex{62}\)

    Redondear al diez más cercano.

    1. 1,492
    2. 1,497
    Contestar
    1. 1,490
    2. 1,500
    Ejercicio\(\PageIndex{63}\)

    Redondear al diez más cercano.

    1. 2,791
    2. 2,795
    Ejercicio\(\PageIndex{64}\)

    Redondear al cien más cercano.

    1. 63,994
    2. 63,940
    Contestar
    1. 64,000
    2. 63,900
    Ejercicio\(\PageIndex{65}\)

    Redondear al cien más cercano.

    1. 49,584
    2. 49,548

    En los siguientes ejercicios, redondear cada número al ⓐ cien, ⓑ mil, ⓒ diez mil más cercano.

    Ejercicio\(\PageIndex{66}\)

    392,546

    Contestar
    1. 392,500
    2. 393,000
    3. 390,000
    Ejercicio\(\PageIndex{67}\)

    619,348

    Ejercicio\(\PageIndex{68}\)

    2,586,991

    Contestar
    1. 2,587,000
    2. 2,587,000
    3. 2,590,000
    Ejercicio\(\PageIndex{69}\)

    4,287,965

    Identificar múltiplos y factores

    En los siguientes ejercicios, utilice las pruebas de divisibilidad para determinar si cada número es divisible por 2, 3, 5, 6 y 10.

    Ejercicio\(\PageIndex{70}\)

    84

    Contestar

    divisible por 2, 3 y 6

    Ejercicio\(\PageIndex{71}\)

    9,696

    Ejercicio\(\PageIndex{72}\)

    75

    Contestar

    divisible por 3 y 5

    Ejercicio\(\PageIndex{73}\)

    78

    Ejercicio\(\PageIndex{74}\)

    900

    Contestar

    divisible por 2, 3, 5, 6 y 10

    Ejercicio\(\PageIndex{75}\)

    800

    Ejercicio\(\PageIndex{76}\)

    986

    Contestar

    divisible por 2

    Ejercicio\(\PageIndex{77}\)

    942

    Ejercicio\(\PageIndex{78}\)

    350

    Contestar

    divisible por 2, 5 y 10

    Ejercicio\(\PageIndex{79}\)

    550

    Ejercicio\(\PageIndex{80}\)

    22,335

    Contestar

    divisible por 3 y 5

    Ejercicio\(\PageIndex{81}\)

    39,075

    Encuentre factorizaciones principales y múltiplos menos comunes

    En los siguientes ejercicios, encuentra la factorización principal.

    Ejercicio\(\PageIndex{82}\)

    86

    Contestar

    \(2\cdot 43\)

    Ejercicio\(\PageIndex{83}\)

    78

    Ejercicio\(\PageIndex{84}\)

    132

    Contestar

    \(2\cdot 2\cdot 3\cdot 11\)

    Ejercicio\(\PageIndex{85}\)

    455

    Ejercicio\(\PageIndex{86}\)

    693

    Contestar

    \(3\cdot 3\cdot 7\cdot 11\)

    Ejercicio\(\PageIndex{87}\)

    400

    Ejercicio\(\PageIndex{88}\)

    432

    Contestar

    \(2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3\cdot 3\)

    Ejercicio\(\PageIndex{89}\)

    627

    Ejercicio\(\PageIndex{90}\)

    2,160

    Contestar

    \(2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3\cdot 3\cdot 5\)

    Ejercicio\(\PageIndex{91}\)

    2,520

    En los siguientes ejercicios, encuentra el múltiplo menos común de cada par de números usando el método de múltiplos.

    Ejercicio\(\PageIndex{92}\)

    8, 12

    Contestar

    24

    Ejercicio\(\PageIndex{93}\)

    4, 3

    Ejercicio\(\PageIndex{94}\)

    12, 16

    Contestar

    48

    Ejercicio\(\PageIndex{95}\)

    30, 40

    Ejercicio\(\PageIndex{96}\)

    20, 30

    Contestar

    60

    Ejercicio\(\PageIndex{97}\)

    44, 55

    En los siguientes ejercicios, encuentra el múltiplo menos común de cada par de números usando el método de factores primos.

    Ejercicio\(\PageIndex{98}\)

    8, 12

    Contestar

    24

    Ejercicio\(\PageIndex{99}\)

    12, 16

    Ejercicio\(\PageIndex{100}\)

    28, 40

    Contestar

    280

    Ejercicio\(\PageIndex{101}\)

    84, 90

    Ejercicio\(\PageIndex{102}\)

    55, 88

    Contestar

    440

    Ejercicio\(\PageIndex{103}\)

    60, 72

    Matemáticas cotidianas

    Ejercicio\(\PageIndex{104}\)

    Escribiendo un Cheque Jorge compró un auto por $24.493. Pagó el auto con cheque. Escribe el precio de compra en palabras.

    Contestar

    veinticuatro mil cuatrocientos noventa y tres dólares

    Ejercicio\(\PageIndex{105}\)

    Redactar un Check La remodelación de cocina de Marissa costó $18,549. Ella le escribió un cheque al contratista. Escribe la cantidad pagada en palabras.

    Ejercicio\(\PageIndex{106}\)

    Comprar un Auto Jorge compró un auto por $24,493. Redondear el precio al más cercano

    1. diez
    2. cien
    3. mil; y
    4. diez mil.
    Contestar
    1. $24,490
    2. 24,500
    3. $24,000
    4. $20,000
    Ejercicio\(\PageIndex{107}\)

    Remodelación de una Cocina La remodelación de la cocina de Marissa costó $18,549, Redondear el costo al más cercano

    1. diez
    2. cien
    3. mil y
    4. diez mil.
    Ejercicio\(\PageIndex{108}\)

    Población La población de China era de 1,339,724,852 al 1 de noviembre de 2010. Redondear la población al más cercano

    1. mil millones
    2. cien millones; y
    3. millones.
    Contestar
    1. 1,000,000,000
    2. 1,300,000,000
    3. 1,340,000,000
    Ejercicio\(\PageIndex{109}\)

    Astronomía La distancia promedio entre la Tierra y el sol es de 149,597,888 kilómetros. Redondear la distancia al más cercano

    1. cien millones
    2. diez millones; y
    3. millones.
    Ejercicio\(\PageIndex{110}\)

    Compras de Abarrotes Los perritos calientes se venden en paquetes de 10, pero los bollos de hot dog vienen en paquetes de ocho. ¿Cuál es el número más pequeño que hace que salgan parejos los hot dogs y los bollos?

    Contestar

    40

    Ejercicio\(\PageIndex{111}\)

    Compras de Abarrotes Los platos de papel se venden en paquetes de 12 y los vasos para fiestas vienen en paquetes de ocho. ¿Cuál es el número más pequeño que hace que los platos y tazas salgan parejos?

    Ejercicios de escritura

    Ejercicio\(\PageIndex{112}\)

    Dar un ejemplo cotidiano donde ayuda redondear números.

    Ejercicio\(\PageIndex{113}\)

    Si un número es divisible por 2 y por 3 ¿por qué también es divisible por 6?

    Ejercicio\(\PageIndex{114}\)

    ¿Cuál es la diferencia entre números primos y números compuestos?

    Contestar

    Las respuestas pueden variar.

    Ejercicio\(\PageIndex{115}\)

    Explica con tus propias palabras cómo encontrar la factorización prima de un número compuesto, usando cualquier método que prefieras.

    Autocomprobación

    ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

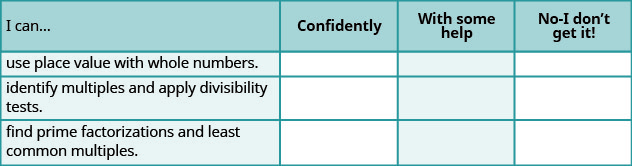
    Se muestra una tabla con cuatro columnas y cuatro filas. Las columnas se titulan “Puedo...”, “Con confianza”, “Con algo de ayuda”, y “¡No, no lo consigo!”. La primera columna tiene tres filas de texto que dicen “usar valor posicional con números enteros”, “identificar múltiplos y aplicar reglas de divisibilidad” y “encontrar factorización prima y múltiplos menos comunes”. Todos los demás espacios de la mesa están en blanco.

    ⓑ Si la mayoría de tus cheques fueron:

    ... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.

    ... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?

    ... no, ¡no lo pillo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.

    This page titled 1.2E: Ejercicios is shared under a not declared license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.