1.2: Introducción a los números enteros

Última actualización
Guardar como PDF

Page ID: 110409

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:
Usar el valor posicionar con números enteros
Identificar múltiplos y aplicar pruebas de divisibilidad
Encuentra factorizaciones principales y múltiplos menos comunes

Al comenzar nuestro estudio del álgebra elemental, necesitamos refrescar algunas de nuestras habilidades y vocabulario. Este capítulo se centrará en números enteros, enteros, fracciones, decimales y números reales. También comenzaremos nuestro uso de la notación algebraica y el vocabulario.

Usar valor posicionar con números enteros

Los números más básicos utilizados en álgebra son los números que usamos para contar objetos en nuestro mundo:$1, 2, 3, 4$, y así sucesivamente. A estos se les llama el número de conteo s. Los números de conteo también se llaman números naturales. Si sumamos cero a los números de conteo, obtenemos el conjunto de números enteros s.

Recuento de números:$1, 2, 3, …$
Números Enteros:$0, 1, 2, 3, …$

La notación “$…$” se llama elipsis y significa “y así sucesivamente”, o que el patrón continúa sin cesar.

Podemos visualizar números de conteo y números enteros en una recta numérica (ver Figura$\PageIndex{1}$).

Una línea numérica horizontal con flechas en cada extremo y valores de cero a seis corre a lo largo de la parte inferior del diagrama. Una segunda línea horizontal con una flecha orientada hacia la izquierda se encuentra por encima de la primera y se extiende de cero a tres. Esta línea está etiquetada como “más pequeña”. Una tercera línea horizontal con una flecha orientada hacia la derecha se encuentra por encima de las dos primeras, pero va de tres a seis y se etiqueta como “más grande”. — Figura$\PageIndex{1}$: Los números en la recta numérica se hacen más grandes a medida que van de izquierda a derecha, y más pequeños a medida que van de derecha a izquierda. Si bien esta recta numérica muestra solo los números enteros$0$ a través$6$, los números siguen sin fin.

Hacer la actividad de Matemáticas Manipulativas “Línea numérica Parte 1” te ayudará a desarrollar una mejor comprensión de los números de conteo y de los números enteros.

Nuestro sistema numérico se llama sistema de valor posicional, porque el valor de un dígito depende de su posición en un número. La figura$\PageIndex{2}$ muestra los valores posicionales. Los valores posicionales se separan en grupos de tres, que se denominan periodos. Los periodos son unos, miles, millones, miles de millones, billones, y así sucesivamente. En un número escrito, las comas separan los periodos.

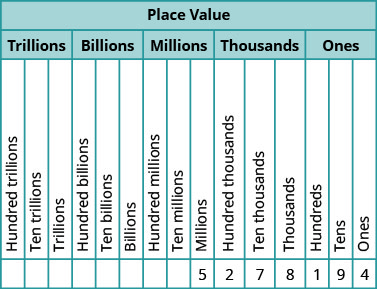
Esta cifra es una tabla que ilustra el número 5,278,194 dentro del sistema de valor posicional. La tabla se muestra con una fila de encabezado, etiquetada como “Valor posicional”, dividida en una segunda fila de encabezado etiquetada como “Trillones”, “Miles de millones”, “Miles” y “Unos”. Bajo el encabezado “Trillones” se encuentran tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien billones”, “Diez billones” y “Trillones”. Bajo el encabezado “Miles de millones” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien miles de millones”, “Diez mil millones” y “Miles de millones”. Bajo el encabezado “Millones” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien millones”, “Diez millones” y “Millones”. Bajo el encabezado “Miles” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien miles”, “Diez miles” y “Miles”. Bajo el encabezado “Unos” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cientos”, “Decenas” y “Unos”. De izquierda a derecha, debajo de las columnas etiquetadas como “Millones”, “Cien miles”, “Diez miles”, “Miles”, “Cientos”, “Decenas” y “Unas”, se encuentran los siguientes valores: 5, 2, 7, 8, 1, 9, 4. Esto significa que hay 5 millones, 2 cientos miles, 7 diez miles, 8 miles, 1 cientos, 9 decenas, y 4 unos en el número cinco millones doscientos setenta y nueve mil ciento noventa y cuatro. — Figura$\PageIndex{2}$: El número$5278194$ se muestra en el gráfico. El dígito$5$ está en el lugar de millones. El dígito$2$ está en el lugar de los cien miles. El dígito$7$ está en el lugar de los diez mil. El dígito$8$ está en el lugar de miles. El dígito$1$ está en el lugar de los cientos. El dígito$9$ está en el lugar de las decenas. El dígito$4$ está en el lugar de unos.

Ejercicio$\PageIndex{1}$

En el número$63407218$, encuentra el valor posicionar de cada dígito:

$7$
$0$
$1$
$6$
$3$

Contestar

Coloque el número en la tabla de valores posicionales:

$Esta figura es una tabla que ilustra el número 63.407.218 dentro del sistema de valor posicional. La tabla se muestra con una fila de encabezado, etiquetada como “Valor posicional”, dividida en una segunda fila de encabezado etiquetada como “Trillones”, “Miles de millones”, “Miles” y “Unos”. Bajo el encabezado “Trillones” se encuentran tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien billones”, “Diez billones” y “Trillones”. Bajo el encabezado “Miles de millones” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien miles de millones”, “Diez mil millones” y “Miles de millones”. Bajo el encabezado “Millones” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien millones”, “Diez millones” y “Millones”. Bajo el encabezado “Miles” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cien miles”, “Diez miles” y “Miles”. Bajo el encabezado “Unos” hay tres columnas etiquetadas, escritas de abajo hacia arriba, que dicen “Cientos”, “Decenas” y “Unos”. De izquierda a derecha, debajo de las columnas etiquetadas “Diez millones”, “Millones”, “Cien miles”, “Diez miles”, “Miles”, “Cientos”, “Decenas” y “Unas”, son los siguientes valores: 6, 3, 4, 0, 7, 2, 1, 8. Esto significa que hay 6 diez millones, 3 millones, 4 cientos miles, 0 diez miles, 7 miles, 2 cientos, 1 diez, y 8 unos en el número sesenta y tres millones, cuatrocientos siete mil, doscientos dieciocho.$

El$7$ está en el lugar de miles.
El$0$ está en el lugar de los diez miles.
El$1$ está en el lugar de las decenas.
El$6$ está en el lugar de los diez millones.
El$3$ está en el lugar de los millones.

Ejercicio$\PageIndex{2}$

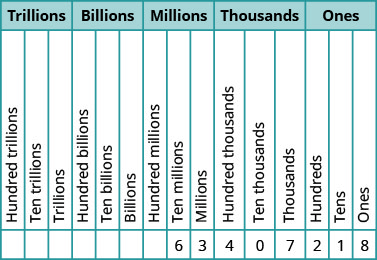
Para el número$27493615$, encuentra el valor posicionar de cada dígito:

Contestar

diez millones
decenas
cien miles
millones
unos

Ejercicio$\PageIndex{3}$

Para el número$519711641328$, encuentra el valor posicionar de cada dígito:

Contestar

miles de millones
diez miles
decenas
cien miles
cien millones

Cuando escribes un cheque, escribes el número en palabras así como en cifras. Para escribir un número en palabras, escriba el número en cada periodo, seguido del nombre del periodo, sin la s al final. Comienza por la izquierda, donde los periodos tienen el mayor valor. El periodo de unos no se nombra. Las comas separan los puntos, así que dondequiera que haya una coma en el número, ponga una coma entre las palabras (ver Figura$\PageIndex{3}$). El número$74218369$ está escrito como setenta y cuatro millones, doscientos dieciocho mil, trescientos sesenta y nueve.

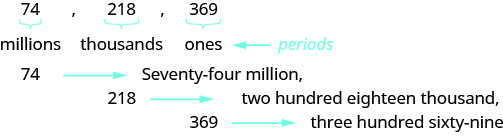
En esta figura se listan en fila los números 74, 218 y 369, separados por comas. Cada número tiene un corchete debajo de él con la palabra “millones” escrita debajo del número 74, “miles” escrita debajo del número 218, y “unos” escrita debajo del número 369. Una flecha orientada hacia la izquierda apunta a estas tres palabras, etiquetándolas como “periodos”. Una fila hacia abajo está el número “74”, una flecha orientada hacia la derecha y las palabras “Setenta y cuatro millones” seguidas de una coma. La siguiente fila de abajo es el número “218”, una flecha orientada hacia la derecha y las palabras “doscientos dieciocho mil” seguidas de una coma. En la fila inferior se encuentra el número “369”, una flecha orientada hacia la derecha y las palabras “trescientos sesenta y nueve”. — Figura$\PageIndex{3}$

NOMBRAR UN NÚMERO ENTERO

Comienza por la izquierda y nombra el número en cada periodo, seguido del nombre del periodo.
Poner comas en el número para separar los periodos.
No nombra el periodo de unos.

Ejercicio$\PageIndex{4}$

Nombra el número$8165432098710$ usando palabras.

Contestar

Nombra el número en cada periodo, seguido del nombre del periodo.

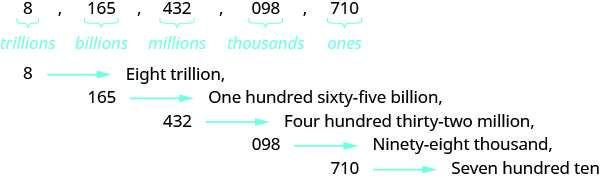
$En esta figura se listan en fila los números 8, 165, 432, 098 y 710, separados por comas. Cada número tiene un paréntesis horizontal debajo con la palabra “billones” escrita debajo del número 8, “miles de millones” escrita debajo del número 165, “millones” escrita debajo del número 432, “miles” escrita debajo del número 098, y “unos” escritos debajo del número 710. Una fila abajo está el número 8, una flecha orientada hacia la derecha y las palabras “Ocho billones” seguidas de una coma. En la siguiente fila de abajo se encuentra el número 165, una flecha orientada hacia la derecha y las palabras “Ciento sesenta y cinco mil millones” seguidas de una coma. En la siguiente fila de abajo se encuentra el número 432, una flecha orientada hacia la derecha y las palabras “Cuatrocientos treinta y dos millones” seguidas de una coma. En la siguiente fila de abajo se encuentra el número “098”, una flecha orientada hacia la derecha y las palabras “Noventa y ocho mil” seguidas de una coma. En la fila inferior se encuentra el número 710, una flecha orientada hacia la derecha y las palabras “Setecientos diez”.$

Poner las comas para separar los periodos.

Entonces,$8165432098710$ se nombra como ocho billones, ciento sesenta y cinco mil, cuatrocientos treinta y dos millones, noventa y ocho mil, setecientos diez.

Ejercicio$\PageIndex{5}$

Nombra el número 9,258,137,904,0619,258,137,904,061 usando palabras.

Contestar: nueve billones, doscientos cincuenta y ocho mil millones, ciento treinta y siete millones, novecientos cuatro mil, sesenta y uno

Ejercicio$\PageIndex{6}$

Nombra el número 17,864,325,619,00417,864,325,619,004 usando palabras.

Contestar: diecisiete billones, ochocientos sesenta y cuatro mil millones, trescientos veinticinco millones, seiscientos diecinueve mil cuatro

Ahora vamos a revertir el proceso escribiendo los dígitos a partir del nombre del número. Para escribir el número en cifras, primero buscamos las palabras clave que indiquen los periodos. Es útil dibujar tres espacios en blanco para los períodos necesarios y luego rellenar los espacios en blanco con los números, separando los puntos con comas.

ESCRIBE UN NUMERO ENTERO

Identificar las palabras que indican periodos. (Recuerda, el periodo unos nunca se nombra.)
Dibuja tres espacios en blanco para indicar el número de lugares necesarios en cada periodo. Separar los periodos por comas.
Nombra el número en cada periodo y coloca los dígitos en la posición correcta del valor posicional.

Ejercicio$\PageIndex{7}$

Escribe nueve mil millones, doscientos cuarenta y seis millones, setenta y tres mil, ciento ochenta y nueve como número entero usando dígitos.

Contestar: Identificar las palabras que indican periodos.
Salvo el primer periodo, todos los demás periodos deberán tener tres plazas. Dibuja tres espacios en blanco para indicar el número de lugares necesarios en cada periodo. Separar los periodos por comas.
Después escribe los dígitos en cada periodo.; $Una imagen tiene dos líneas de texto. Las líneas superiores decían “nueve mil millones”, seguida de una coma, y “doscientos cuarenta y seis millones”, seguida también de una coma. Las palabras “mil millones” y “millones” están subrayadas y cada frase tiene un corchete debajo. En las líneas inferiores se lee “setenta y tres mil”, seguido de una coma, y “ciento ochenta y nueve”. La palabra “mil” está subrayada y cada frase tiene un corchete debajo.$; El número es de 9,246,073,189.

Ejercicio$\PageIndex{8}$

Escribe el número dos mil millones, cuatrocientos sesenta y seis millones, setecientos catorce mil, cincuenta y uno como número entero usando dígitos.

Contestar: 2,466,714.051

Ejercicio$\PageIndex{9}$

Escribe el número once mil millones, novecientos veintiún millones, ochocientos treinta mil, ciento seis como número entero usando dígitos.

Contestar: 11,921,830,106

En 2013, la Oficina del Censo de Estados Unidos estimó la población del estado de Nueva York en 19,651,127 habitantes. Podríamos decir que la población de Nueva York era de aproximadamente 20 millones. En muchos casos, no necesitas el valor exacto; un número aproximado es lo suficientemente bueno.

El proceso de aproximación de un número se llama redondeo. Los números se redondean a un valor posicional específico, dependiendo de la precisión que se necesite. Decir que la población de Nueva York es de aproximadamente 20 millones significa que redondeamos al lugar de millones.

Ejercicio$\PageIndex{10}$ How to Round Whole Numbers

Vuelta 23,658 al cien más cercano.

Contestar: $Esta figura es una tabla que tiene tres columnas y cuatro filas. La primera columna es una columna de encabezado, y contiene los nombres y números de cada paso. La segunda columna contiene instrucciones escritas adicionales. La tercera columna contiene los números correspondientes a los pasos e instrucciones escritos. En la fila superior, la primera celda dice: “Paso 1. Localice el valor posicional dado con una flecha. Todos los dígitos a la izquierda no cambian”. En la segunda celda, las instrucciones dicen: “Localiza los cientos colocan en 23 mil 658”. En la tercera celda, está el número 23,658 con una flecha apuntando al dígito 6, etiquetándolo como “lugar de cientos”.$ $Una fila más abajo, las instrucciones en la primera celda dicen: “Paso 2. Subrayar el dígito a la derecha del valor positorio dado”. En la segunda celda, las instrucciones dicen: “Subrayar el 5, que está a la derecha del lugar de los cientos”. En la tercera celda, está nuevamente el número 23,658, la misma flecha apuntando al dígito 6, etiquetándolo el lugar de los cientos. El 5 también está subrayado en esta celda.$ $Una fila más abajo, la primera celda dice: “Paso 3. ¿Este dígito es mayor o igual a 5? sí: agregue 1 al dígito en el valor posicional dado. No: no cambie el dígito en el valor posicionar dado”. En la segunda celda, las instrucciones dicen: “Agrega 1 al 6 en el lugar de los cientos, ya que 5 es mayor o igual a 5”. La tercera celda contiene nuevamente el número 23,658, con una flecha apuntando al dígito 6 y el texto “agregar 1”. También hay un corchete debajo de los dígitos 5 y 8, con una flecha apuntando a ellos y el texto “reemplazar con 0s”.$ $En la fila inferior, la primera celda dice: “Paso 4. Reemplazar todos los dígitos a la derecha del valor posicionar dado por ceros. Entonces, 23,700 se redondea al centenar más cercano”. En la segunda celda, las instrucciones dicen: “Reemplazar todos los dígitos a la derecha del lugar de los cientos por ceros”. La tercera celda contiene el número 23,700, al que hemos llegado redondeando el número 23,658 al cien más cercano.$

Ejercicio$\PageIndex{11}$

Redonda al cien más cercano: 17,852.

Contestar: 17,900

Ejercicio$\PageIndex{12}$

Redonda al cien más cercano: 468,751.

Contestar: 468,800

NÚMEROS ENTEROS

Localice el valor positorio dado y márquelo con una flecha. Todos los dígitos a la izquierda de la flecha no cambian.
Subrayar el dígito a la derecha del valor positorio dado.
¿Este dígito es mayor o igual a 5?
- sí: agregue 11 al dígito en el valor posicional dado.
- no: no cambie el dígito en el valor posicionar dado.
Reemplazar todos los dígitos a la derecha del valor posicionar dado por ceros.

Ejercicio$\PageIndex{13}$

Vuelta 103,978103,978 a la más cercana:

cien
mil
diez mil

Contestar

Localiza el lugar de los cientos en 103,978.	$.$
Subrayar el dígito a la derecha del lugar de los cientos.	$.$
Dado que 7 es mayor o igual a 5, agregue 1 al 9. Reemplaza todos los dígitos a la derecha del lugar de los cientos por ceros.	$.$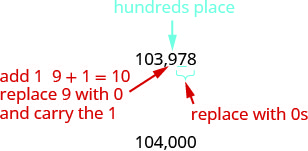
	Entonces, 104,000 son 103,978 redondeados al cien más cercano.

Localice el lugar de miles y subraye el dígito a la derecha del lugar de miles.	$.$
Dado que 9 es mayor o igual a 5, agregue 1 al 3. Reemplaza todos los dígitos a la derecha del lugar de los cientos por ceros.	$.$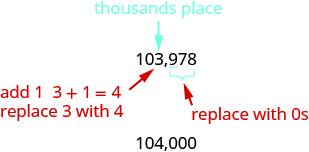
	Entonces, 104 mil es 103 mil 978 redondeados al mil más cercano.

Localice el lugar de los diez miles y subraye el dígito a la derecha del lugar de los diez miles.	$.$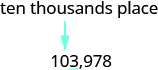
Dado que 3 es menor que 5, dejamos el 0 tal cual, y luego reemplazamos los dígitos a la derecha por ceros.	$.$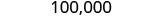
	Entonces, 100,000 son 103,978 redondeados a los diez mil más cercanos.

Ejercicio$\PageIndex{14}$

Vuelta 206,981 al más cercano: 1. cien 2. mil 3. diez mil.

Contestar

207,000
207,000
210,000

Ejercicio$\PageIndex{15}$

Vuelta 784,951 al más cercano: 1. cien 2. mil 3. diez mil.

Contestar

785,000
785,000
780,000

Identificar múltiplos y aplicar pruebas de divisibilidad

Los números 2, 4, 6, 8, 10 y 12 se denominan múltiplos de 2. Se puede escribir un múltiplo de 2 como producto de un número de conteo y 2.

Diagrama compuesto por dos filas de números. La fila superior dice “2, 4, 6, 8, 10, 12”, seguida de una elipsis. Por debajo de 2 es 2 veces 1, por debajo de 4 es 2 por 2, por debajo de 6 es 2 por 3, por debajo de 8 es 2 por 4, por debajo de 10 es 2 por 5, y por debajo de 12 es 2 por 6. — Figura$\PageIndex{4}$

De igual manera, un múltiplo de 3 sería producto de un número de conteo y 3.

Diagrama compuesto por dos filas de números. La fila superior dice “3, 6, 9, 12, 15, 18”, seguida de una elipsis. Por debajo de 3 es 3 veces 1, por debajo de 6 es 3 por 2, por debajo de 9 es 3 por 3, por debajo de 12 es 3 por 4, por debajo de 15 es 3 por 5, y por debajo de 18 es 3 por 6. — Figura$\PageIndex{5}$

Podríamos encontrar los múltiplos de cualquier número continuando con este proceso.

Nota

Hacer la actividad de Matemáticas Manipulativas “Multiples” te ayudará a desarrollar una mejor comprensión de los múltiplos.

En el cuadro se$\PageIndex{1}$ muestran los múltiplos del 2 al 9 para los primeros 12 números de conteo.

Mesa$\PageIndex{1}$
Número de conteo	1	2	3	4	5	6	7	8	9	10	11	12
Multiplos de 2	2	4	6	8	10	12	14	16	18	20	22	24
Multiplos de 3	3	6	9	12	15	18	21	24	27	30	33	36
Multiplos de 4	4	8	12	16	20	24	28	32	36	40	44	48
Multiplos de 5	5	10	15	20	25	30	35	40	45	50	55	60
Multiplos de 6	6	12	18	24	30	36	42	48	54	60	66	72
Multiplos de 7	7	14	21	28	35	42	49	56	63	70	77	84
Multiplos de 8	8	16	24	32	40	48	56	64	72	80	88	96
Multiplos de 9	9	18	27	36	45	54	63	72	81	90	99	108
Multiplos de 10	10	20	30	40	50	60	70	80	90	100	110	120

MÚLTIPLE DE

Un número es un múltiplo de$n$ si es producto de un número de conteo y$n$.

Otra forma de decir que 15 es un múltiplo de 3 es decir que 15 es divisible por 3. Eso quiere decir que cuando dividimos 3 en 15, obtenemos un número de conteo. De hecho,$15\div 3$ es 5, entonces 15 lo es$5\cdot3$.

DIVISIBLE POR UN NUMERO

Si un número$m$ es un múltiplo de$n$, entonces$m$ es divisible por$n$

Mira los múltiplos de$5$ en Tabla$\PageIndex{1}$. Todos terminan en 5 o 0. Los números con último dígito de 5 o 0 son divisibles por 5. Buscando otros patrones en la Tabla$\PageIndex{1}$ que muestre múltiplos de los números del 2 al 9, podemos descubrir las siguientes pruebas de divisibilidad:

Tests de divisibilidad

Un número es divisible por:

2 si el último dígito es 0, 2, 4, 6 u 8.
3 si la suma de los dígitos es divisible por 3.
5 si el último dígito es 5 o 0.
6 si es divisible tanto por 2 como por 3.
10 si termina con 0.

Ejercicio$\PageIndex{16}$

¿Es 5625 divisible por 2? ¿Por 3? ¿Por 5? ¿Por 6? ¿Por 10?

Contestar

\[\begin{array} {ll} {\text{Is 5625 divisible by 2?}} &{} \\ {\text{Does it end in 0, 2, 4, 6, or 8?}} &{\text{No.}} \\ {} &{\text{5625 is not divisible by 2.}} \end{array}\]

\[\begin{array} {ll} {\text{Is 5625 divisible by 3?}} &{} \\ {\text{What is the sum of the digits?}} &{5 + 6 + 2 + 5 = 18} \\ {\text{Is the sum divisible by 3?}} &{\text{Yes, 5625 is divisible by 3.}} \end{array}\]

\[\begin{array} {ll} {\text{Is 5625 divisible by 5 or 10?}} &{} \\ {\text{What is the last digit? It is 5.}} &{\text{5625 is divisible by 5 but not by 10.}} \end{array}\]

\[\begin{array} {ll} {\text{Is 5625 divisible by 6?}} &{} \\ {\text{Is it divisible by both 2 and 3?}} &{\text{No, 5625 is not divisible by 2, so 5625 is }} \\ {} &{\text{not divisible by 6.}}\end{array}\]

Ejercicio$\PageIndex{17}$

Determinar si 4.962 es divisible por 2, por 3, por 5, por 6 y por 10.

Contestar: por 2, 3 y 6

Ejercicio$\PageIndex{18}$

Determinar si 3,765 es divisible por 2, por 3, por 5, por 6 y por 10.

Contestar: por 3 y 5

Encuentre factorizaciones principales y múltiplos menos comunes

En matemáticas, a menudo hay varias formas de hablar de las mismas ideas. Hasta el momento, hemos visto que si$m$ es un múltiplo de$n$, podemos decir que$m$ es divisible por$n$. Por ejemplo, dado que 72 es un múltiplo de 8, decimos que 72 es divisible por 8. Dado que 72 es múltiplo de 9, decimos 72 es divisible por 9. Podemos expresarlo aún de otra manera.

Ya que$8\cdot 9=72$, decimos que 8 y 9 son factores de 72. Cuando escribimos$72=8\cdot 9$, decimos que hemos factorizado 72.

Otras formas de factorizar 72 son$1\cdot 72$$2\cdot 36$,,$3\cdot 24$,$4\cdot 18$ y$6\cdot 12$. Setenta y dos tiene muchos factores: 1, 2, 3, 4, 6, 8, 9, 12, 18, 36 y 72.

FACTORES

Si$a\cdot b=m$, entonces$a$ y$b$ son factores de$m$.

Algunos números, como 72, tienen muchos factores. Otros números tienen sólo dos factores.

Nota

Hacer la actividad de Matemáticas Manipulativas “Multiplicación de modelos y factorización” te ayudará a desarrollar una mejor comprensión de la multiplicación y factorización.

Número primo y número compuesto

Un número primo es un número de conteo mayor que 1, cuyos únicos factores son 1 y él mismo.

Un número compuesto es un número de conteo que no es primo. Un número compuesto tiene factores distintos a 1 y a sí mismo.

Nota

Hacer la actividad de Matemáticas Manipulativas “Prime Numbers” te ayudará a desarrollar una mejor comprensión de los números primos.

Los números de conteo del 2 al 19 se listan en la Figura$\PageIndex{7}$, con sus factores. ¡Asegúrate de estar de acuerdo con la etiqueta “prime” o “composite” para cada una!

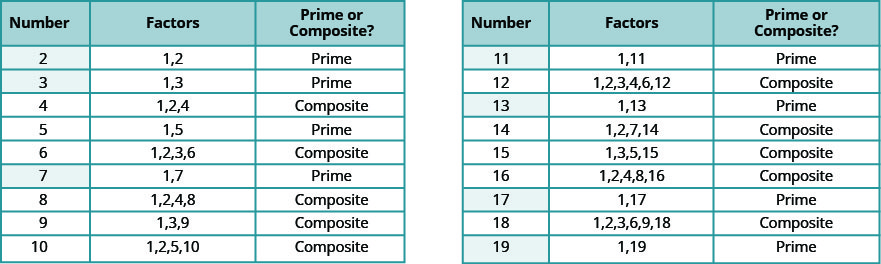
Se muestra una tabla con once filas y siete columnas. La primera fila es una fila de encabezado, y cada celda etiqueta el contenido de la columna debajo de ella. En la fila del encabezado, las tres primeras celdas leen de izquierda a derecha “Número”, “Factores” y “¿Prime o Composite?” Toda la cuarta columna está en blanco. Las últimas tres celdas leen de izquierda a derecha “Número”, “Factor” y “¿Prime o Composite?” otra vez. En cada fila posterior, la primera celda contiene un número, la segunda contiene sus factores y la tercera indica si el número es primo o compuesto. Las tres columnas a la izquierda de la columna central en blanco contienen esta información para el número 2 al 10, y las tres columnas a la derecha de la columna central en blanco contienen esta información para el número 11 al 19. En el lado izquierdo de la columna en blanco, en la primera fila debajo de la fila de encabezado, las celdas leen de izquierda a derecha: “2”, “1,2” y “Prime”. En la siguiente fila, las celdas leen de izquierda a derecha: “3”, “1,3” y “Prime”. En la siguiente fila, las celdas leen de izquierda a derecha: “4”, “1,2,4” y “Composite”. En la siguiente fila, las celdas leen de izquierda a derecha: “5”, “1,5” y “Prime”. En la siguiente fila, las celdas leen de izquierda a derecha: “6”, “1,2,3,6” y “Composite”. En la siguiente fila, las celdas leen de izquierda a derecha: “7”, “1,7” y “Prime”. En la siguiente fila, las celdas leen de izquierda a derecha: “8”, “1,2,4,8” y “Composite”. En la siguiente fila, las celdas leen de izquierda a derecha: “9”, “1,3,9” y “Composite”. En la fila inferior, las celdas leen de izquierda a derecha: “10”, “1,2,5,10” y “Composite”. En el lado derecho de la columna en blanco, en la primera fila debajo de la fila de encabezado, las celdas leen de izquierda a derecha: “11”, “1,11” y “Prime”. En la siguiente fila, las celdas decían de izquierda a derecha: “12”, “1,2,3,4,6,12” y “Composite”. En la siguiente fila, las celdas leen de izquierda a derecha: “13”, “1,13” y “Prime”. En la siguiente fila, las celdas leen de izquierda a derecha “14”, “1,2,7,14” y “Composite”. En la siguiente fila, las celdas leen de izquierda a derecha: “15”, “1,3,5,15” y “Composite”. En la siguiente fila, las celdas decían de izquierda a derecha: “16”, “1,2,4,8,16” y “Composite”. En la siguiente fila, las celdas leen de izquierda a derecha, “17”, “1,17” y “Prime”. En la siguiente fila, las celdas leen de izquierda a derecha, “18”, “1,2,3,6,9,18” y “Compuesto”. En la fila inferior, las celdas leen de izquierda a derecha: “19”, “1,19” y “Prime”. — Figura$\PageIndex{7}$

Los números primos menores a 20 son 2, 3, 5, 7, 11, 13, 17 y 19. Observe que el único número primo par es 2.

Un número compuesto se puede escribir como un producto único de primos. A esto se le llama la factorización prima del número. Encontrar la factorización prima de un número compuesto será útil más adelante en este curso.

FACTORIZACIÓN PRIME

La descomposición de un número primo es el producto de números primos que es igual al número.

Para encontrar la factorización prima de un número compuesto, busque dos factores cualesquiera del número y utilícelos para crear dos ramas. Si un factor es primo, esa rama está completa. ¡Circula ese primo!

Si el factor no es primo, encuentra dos factores del número y continúa con el proceso. Una vez que todas las ramas tienen cebos en círculo al final, la factorización se completa. El número compuesto ahora se puede escribir como un producto de números primos.

Ejercicio$\PageIndex{19}$

Factor 48.

Contestar

$Esta figura es una tabla que tiene tres columnas y cuatro filas. La primera columna es una columna de encabezado, y contiene los nombres y números de cada paso. La segunda columna contiene más instrucciones escritas y algunas matemáticas. La tercera columna contiene la mayor parte del trabajo matemático correspondiente a los pasos e instrucciones escritos. En la fila superior, la primera celda dice: “Paso 1. Encuentra dos factores cuyo producto es el número dado. Usa estos números para crear dos ramas”. La segunda celda contiene la ecuación algebraica 48 es igual a 2 por 24. En la tercera celda, hay un árbol factorial con 48 en la parte superior. Dos ramas descienden de 48 y terminan en 2 y 24 respectivamente.$ $Una fila más abajo, las instrucciones en la primera celda dicen: “Paso 2. Si un factor es primo, esa rama está completa. Da un círculo a la prima”. En la segunda celda, las instrucciones dicen: “2 es primo. Da un círculo a la prima”. En la tercera celda, se repite el árbol de factores del paso 1, pero el 2 en la parte inferior del árbol ahora está en un círculo.$ $Una fila más abajo, la primera celda dice: “Paso 3. Si un factor no es primo, escríbelo como producto de dos factores y continúe el proceso”. En la segunda celda, las instrucciones dicen: “24 no es primo. Romper en 2 factores más”. La tercera celda contiene el árbol factorial original, con 48 en la parte superior y dos ramas apuntando hacia abajo terminando en 2, que está subrayado, y 24. Dos ramas más descienden de 24 y terminan en 4 y 6 respectivamente. Una línea abajo, las instrucciones en el medio de la celda dicen “4 y 6 no son primos. Dividirlos cada uno en dos factores”. En la celda de la derecha, el árbol factorial se repite una vez más. Dos ramas descienden del 4 y terminan en 2 y 2. Ambos 2s están rodeados. Dos ramas más descienden de 6 y terminan en un 2 y un 3, los cuales están ambos en un círculo. Las instrucciones de la izquierda dicen “2 y 3 son primos, así que enciérralos”.$ $En la fila inferior, la primera celda dice: “Paso 4. Escriba el número compuesto como el producto de todos los primos en un círculo”. La segunda celda se deja en blanco. La tercera celda contiene la ecuación algebraica 48 es igual a 2 veces 2 veces 2 veces 2 veces 3.$

Decimos que$2\cdot 2\cdot 2\cdot 2\cdot 3$ es la factorización prima de 48. Generalmente escribimos los primos en orden ascendente. ¡Asegúrate de multiplicar los factores para verificar tu respuesta!

Si primero factorizamos 48 de una manera diferente, por ejemplo as$6\cdot 8$, el resultado seguiría siendo el mismo. Termina la factorización prime y verifica esto por ti mismo.

Ejercicio$\PageIndex{20}$

Encuentra la factorización prima de 80.

Contestar: $2\cdot 2\cdot 2\cdot 2\cdot 5$

Ejercicio$\PageIndex{21}$

Encuentra la factorización prime de 60.

Contestar: $2\cdot 2\cdot 3\cdot 5$

ENCUENTRA LA FACTORIZACION PRIMERA DE UN NÚMERO

Encuentra dos factores cuyo producto es el número dado, y usa estos números para crear dos ramas.
Si un factor es primo, esa rama está completa. Encierra en círculo la flor, como un capullo en el árbol.
Si un factor no es primo, escríbelo como producto de dos factores y continúe el proceso.
Escriba el número compuesto como el producto de todos los primos en un círculo.

Ejercicio$\PageIndex{22}$

Encuentra la factorización primo de 252.

Contestar

Paso 1. Encuentra dos factores cuyo producto es 252. 12 y 21 no son primos. Rompe 12 y 21 en dos factores más. Continuar hasta que se factoricen todos los primos.	$.$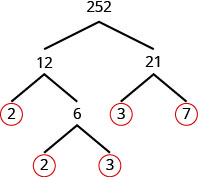
Paso 2. Escribe 252 como producto de todos los primos en círculo.	$252=2\cdot 2\cdot 3\cdot 3\cdot 7$

Ejercicio$\PageIndex{23}$

Encuentra la factorización prima de 126.

Contestar: $2\cdot 3\cdot 3\cdot 7$

Ejercicio$\PageIndex{24}$

Encuentra la factorización prima de 294.

Contestar: $2\cdot 3\cdot 7\cdot 7$

Una de las razones por las que miramos múltiplos y primos es utilizar estas técnicas para encontrar el múltiplo menos común de dos números. Esto será útil cuando sumemos y restemos fracciones con diferentes denominador s. dos métodos se utilizan con mayor frecuencia para encontrar el múltiplo menos común y veremos ambos.

El primer método es el Método de Listado Multiples. Para encontrar el múltiplo menos común de 12 y 18, enumeramos los primeros múltiplos de 12 y 18:

Se muestran dos filas de números. La primera fila comienza con 12, seguida de dos puntos, luego 12, 24, 36, 48, 60, 72, 84, 96, 108, y una elipsis. 36, 72 y 108 están escritas en negritas en rojo. La segunda fila comienza con 18, seguida de dos puntos, luego 18, 36, 54, 72, 90, 108, y una elipsis. Nuevamente, los números 36, 72 y 108 están escritos en negrilla en rojo. En la línea de abajo se encuentra la frase “Multiplos comunes”, dos puntos y los números 36, 72 y 108, escritos en rojo. Una línea a continuación se encuentra la frase “Mínimo Común Múltiple”, dos puntos y el número 36, escrito en azul. — Figura$\PageIndex{8}$

Observe que algunos números aparecen en ambas listas. Son los múltiplos comunes de 12 y 18.

Vemos que los primeros múltiplos comunes de 12 y 18 son 36, 72 y 108. Dado que 36 es el más pequeño de los múltiplos comunes, lo llamamos el múltiplo menos común. A menudo usamos la abreviatura LCM.

MÚLTIPLE

El múltiplo menos común (LCM) de dos números es el número más pequeño que es un múltiplo de ambos números.

El cuadro de procedimiento enumera los pasos a seguir para encontrar el LCM usando el método de factores primos que usamos anteriormente para 12 y 18.

ENCUENTRA EL MÚLTIPLE MENOS COM

Enumere varios múltiplos de cada número.
Busca el número más pequeño que aparece en ambas listas.
Este número es el LCM.

Ejercicio$\PageIndex{25}$

Encuentra el múltiplo menos común de 15 y 20 enumerando múltiplos.

Contestar

Haz listas de los primeros múltiplos de 15 y de 20, y úsalos para encontrar el múltiplo menos común.	$.$
Busca el número más pequeño que aparece en ambas listas.	El primer número que aparece en ambas listas es 60, por lo que 60 es el múltiplo menos común de 15 y 20.

Observe que 120 está en ambas listas, también. Es un múltiplo común, pero no es el múltiplo menos común.

Ejercicio$\PageIndex{26}$

Encuentra el múltiplo menos común enumerando múltiplos: 9 y 12.

Contestar: $36$

Ejercicio$\PageIndex{27}$

Encuentra el múltiplo menos común enumerando múltiplos: 18 y 24.

Contestar: $72$

Nuestro segundo método para encontrar el múltiplo menos común de dos números es usar el método de los factores primos. Volvamos a encontrar el LCM de 12 y 18, esta vez usando sus factores primos.

Ejercicio$\PageIndex{28}$

Encuentra el Múltiple Mínimo Común (MCM) de 12 y 18 usando el método de factores primos.

Contestar: $Esta figura es una tabla que tiene tres columnas y cuatro filas. La primera columna es una columna de encabezado, y contiene los nombres y números de cada paso. La segunda columna contiene más instrucciones escritas y algunas matemáticas. La tercera columna contiene la mayor parte del trabajo matemático correspondiente a los pasos e instrucciones escritos. En la fila superior, la primera celda dice: “Paso 1. Escribe cada número como producto de primos”. La segunda celda se deja en blanco. En la tercera celda, hay dos árboles de factores. En el primer árbol factorial, dos ramas descienden de 18 y terminan en 3 y 6 respectivamente. El 3 es primo y por lo tanto está encerrado en un círculo. Dos ramas más descienden de la 6 y terminan en 2 y 3, las cuales están encerradas en un círculo. En el árbol del segundo factor, dos ramas descienden de 12 y terminan en 3 y 4. El 3 está en un círculo. Dos ramas más descienden de 4, terminando en 2 y 2, las cuales están encerradas en un círculo.$ $Una fila más abajo, las instrucciones en la primera celda dicen: “Paso 2. Enumere los números primos de cada número. Haga coincidir los primos verticalmente cuando sea posible”. En la segunda celda, las instrucciones dicen: “Listar los primos de 12. Enumere los primos de 18. Alinee con los primos de 12 cuando sea posible. Si no se crea una nueva columna”. La tercera celda contiene la factorización prima de 12 escrita ya que la ecuación 12 es igual a 2 veces 2 por 3. Debajo de esta ecuación hay otra que muestra la factorización prima de 18 escrita como la ecuación 18 es igual a 2 veces 3 por 3. Las dos ecuaciones se alinean verticalmente en el símbolo igual. El primero 2 en la factorización prima de 12 se alinea con el 2 en la factorización prima de 18. Bajo el segundo 2 en la factorización prima de 12 hay una brecha en la factorización prima de 18. Bajo el 3 en la factorización prima de 12 es el primero 3 en la factorización primo de 18. El segundo 3 en la desfactorización primo no tiene factores por encima de él de la factorización primo de 12.$ $Una fila abajo, las instrucciones en la primera celda dicen: “Baje el número de cada columna”. La segunda celda está en blanco. La tercera celda contiene nuevamente las factorizaciones primos de 12 y 18, ilustradas como dos ecuaciones alineadas tal como estaban antes. Esta vez, se dibuja una línea horizontal bajo la factorización prima de 18. Debajo de esta línea está la ecuación LCM igual a 2 veces 2 veces 3 veces 3 veces 3. Las flechas se dibujan verticalmente desde la factorización prima de 12 hasta la factorización principal de 18 terminando en la ecuación LCM. La primera flecha comienza en los primeros 2 en la factorización prima de 12 y continúa hacia abajo a través de la 2 en la factorización prima de 18, terminando con los primeros 2 en la LCM. La segunda flecha comienza en los 2 siguientes en la factorización prima de 12 y continúa hacia abajo a través de la brecha en la factorización principal de 18, terminando con la segunda 2 en la LCM. La tercera flecha comienza en el 3 en la factorización prima de 12 y continúa hacia abajo a través de los primeros 3 en la factorización prima de 18, terminando con los primeros 3 en la LCM. La última flecha comienza en el segundo 3 en la factorización principal de 18 y apunta hacia abajo a la segunda 3 en el LCM.$ $En la fila inferior de la tabla, la primera celda dice: “Paso 4: Multiplica los factores”. La segunda celda es de banco. La tercera celda contiene la ecuación LCM es igual a 36.$

Observe que los factores primos de$12(2\cdot 2\cdot 3)$ y los factores primos de$18(2\cdot 3\cdot 3)$ están incluidos en el MCM$(2\cdot 2\cdot 3\cdot 3)$. Entonces 36 es el múltiplo menos común de 12 y 18.

Al hacer coincidir los primos comunes, cada factor primo común se usa solo una vez. De esta manera estás seguro que 36 es el múltiplo menos común.

Ejercicio$\PageIndex{29}$

Encuentra el LCM usando el método de factores primos: 9 y 12.

Contestar: $36$

Ejercicio$\PageIndex{30}$

Encuentra el LCM usando el método de factores primos: 18 y 24.

Contestar: $72$

ENCONTRAR EL MÚLTIPLE MENOS COMÚN UTIL

Escribe cada número como producto de primos.
Enumere los números primos de cada número. Haga coincidir los primos verticalmente cuando sea posible.
Derriba las columnas.
Multiplicar los factores.

Ejercicio$\PageIndex{31}$

Encuentra el Múltiple Mínimo Común (MCM) de 24 y 36 usando el método de factores primos.

Contestar

Encuentra los primos de 24 y 36. Haga coincidir los primos verticalmente cuando sea posible. Derriba todas las columnas.	$.$
Multiplicar los factores.	$.$
	El LCM de 24 y 36 es 72.

Ejercicio$\PageIndex{32}$

Encuentra el LCM usando el método de factores primos: 21 y 28.

Contestar: $84$

Ejercicio$\PageIndex{33}$

Encuentra el LCM usando el método de factores primos: 24 y 32.

Contestar: $96$

Nota

Acceda a este recurso en línea para obtener instrucción adicional y práctica con el uso de números enteros. Necesitará habilitar Java en su navegador web para usar la aplicación.

Tamiz de Eratóstenes

Conceptos clave

Valor posicionar como en la Figura.
Nombra un número entero en palabras
1. Comienza por la izquierda y nombra el número en cada periodo, seguido del nombre del periodo.
2. Poner comas en el número para separar los periodos.
3. No nombra el periodo de unos.
Escribir un número entero usando dígitos
1. Identificar las palabras que indican periodos. (Recuerde que el período de unos nunca se nombra.)
2. Dibuja 3 espacios en blanco para indicar el número de lugares necesarios en cada periodo. Separar los periodos por comas.
3. Nombra el número en cada periodo y coloca los dígitos en la posición correcta del valor posicional.
Números Redondos Enteros
1. Localice el valor positorio dado y márquelo con una flecha. Todos los dígitos a la izquierda de la flecha no cambian.
2. Subrayar el dígito a la derecha del valor positorio dado.
3. ¿Este dígito es mayor o igual a 5?
  - sí: agregue 1 al dígito en el valor posicional dado.
  - no: no cambie el dígito en el valor posicionar dado.
4. Reemplazar todos los dígitos a la derecha del valor posicionar dado por ceros.
Pruebas de divisibilidad: Un número es divisible por:
- 2 si el último dígito es 0, 2, 4, 6 u 8.
- 3 si la suma de los dígitos es divisible por 3.
- 5 si el último dígito es 5 o 0.
- 6 si es divisible tanto por 2 como por 3.
- 10 si termina con 0.
Encuentre la factorización principal de un número compuesto
1. Encuentra dos factores cuyo producto es el número dado, y usa estos números para crear dos ramas.
2. Si un factor es primo, esa rama está completa. Encierra en círculo la flor, como un capullo en el árbol.
3. Si un factor no es primo, escríbelo como producto de dos factores y continúe el proceso.
4. Escriba el número compuesto como el producto de todos los primos en un círculo.
Encuentre el múltiplo menos común enumerando múltiplos
1. Enumere varios múltiplos de cada número.
2. Busca el número más pequeño que aparece en ambas listas.
3. Este número es el LCM.
Encuentre el múltiplo menos común usando el método de factores primos
1. Escribe cada número como producto de primos.
2. Enumere los números primos de cada número. Haga coincidir los primos verticalmente cuando sea posible.
3. Derriba las columnas.
4. Multiplicar los factores.

Glosario

número compuesto: Un número compuesto es un número de conteo que no es primo. Un número compuesto tiene factores distintos a 1 y a sí mismo.

contar números: Los números de conteo son los números 1, 2, 3,...

divisible por un número: Si un número$m$ es un múltiplo de$n$, entonces$m$ es divisible por$n$. (Si 6 es múltiplo de 3, entonces 6 es divisible por 3.)

factores: Si$a\cdot b=m$, entonces$a$ y$b$ son factores de$m$. Desde$3 \cdot 4 = 12$ entonces 3 y 4 son factores de 12.

mínimo común múltiplo: El múltiplo menos común de dos números es el número más pequeño que es un múltiplo de ambos números.

múltiplo de un número: Un número es un múltiplo de$n$ si es producto de un número de conteo y$n$.

línea numérica: Se utiliza una línea numérica para visualizar números. Los números en la recta numérica se hacen más grandes a medida que van de izquierda a derecha, y más pequeños a medida que van de derecha a izquierda.

origen: El origen es el punto etiquetado como 0 en una recta numérica.

factorización prima: La desfactorización de un número es el producto de números primos que es igual al número.

número primo: Un número primo es un número de conteo mayor que 1, cuyos únicos factores son 1 y él mismo.

números enteros: Los números enteros son los números 0, 1, 2, 3,...

Paso 1. Encuentra dos factores cuyo producto es 252. 12 y 21 no son primos. Rompe 12 y 21 en dos factores más. Continuar hasta que se factoricen todos los primos.	$.$
Paso 2. Escribe 252 como producto de todos los primos en círculo.	\(252=2\cdot 2\cdot 3\cdot 3\cdot 7\)

Objetivos de aprendizaje

Usar valor posicionar con números enteros

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

NOMBRAR UN NÚMERO ENTERO

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

ESCRIBE UN NUMERO ENTERO

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\) How to Round Whole Numbers

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

NÚMEROS ENTEROS

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Identificar múltiplos y aplicar pruebas de divisibilidad

Nota

MÚLTIPLE DE

DIVISIBLE POR UN NUMERO

Tests de divisibilidad

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Encuentre factorizaciones principales y múltiplos menos comunes

FACTORES

Nota

Número primo y número compuesto

Nota

FACTORIZACIÓN PRIME

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

ENCUENTRA LA FACTORIZACION PRIMERA DE UN NÚMERO

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

MÚLTIPLE

ENCUENTRA EL MÚLTIPLE MENOS COM

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

ENCONTRAR EL MÚLTIPLE MENOS COMÚN UTIL

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Ejercicio\(\PageIndex{33}\)

Nota

Conceptos clave

Glosario