2.2E: Ejercicios
- Page ID
- 110259
La práctica hace la perfección
Resolver ecuaciones usando las propiedades de división y multiplicación de la igualdad
En los siguientes ejercicios, resuelve cada ecuación usando las Propiedades de División y Multiplicación de Igualdad y comprueba la solución.
\(8x=56\)
- Contestar
-
\(x=7\)
\(7 p=63\)
\(-5 c=55\)
- Contestar
-
\(c=-11\)
\(-9 x=-27\)
\(-809=15 y\)
- Contestar
-
\(y = -\frac{809}{15}\)
\(-731=19 y\)
\(-37 p=-541\)
- Contestar
-
\(p=-\frac{541}{37}\)
\(-19 m=-586\)
\(0.25 z=3.25\)
- Contestar
-
z= 13
\(0.75 a=11.25\)
\(-13x=0\)
- Contestar
-
\(x=0\)
\(24x=0\)
\(\frac{x}{4} = 35\)
- Contestar
-
\(x=140\)
\(\frac{z}{2}=54\)
\(-20=\frac{q}{-5}\)
- Contestar
-
\(q=100\)
\(\frac{c}{-3}=-12\)
\(\frac{y}{9}=-16\)
- Contestar
-
\(y=-144\)
\(\frac{q}{6}=-38\)
\(\frac{m}{-12}=45\)
- Contestar
-
\(m=-540\)
\(-24=\frac{p}{-20}\)
\(-y=6\)
- Contestar
-
\(y=-6\)
\(-u=15\)
\(-v=-72\)
- Contestar
-
\(v=72\)
\(-x=-39\)
\(\frac{2}{3} y=48\)
- Contestar
-
\(y=72\)
\(\frac{3}{5} r=75\)
\(-\frac{5}{8} w=40\)
- Contestar
-
\(w=-64\)
\(24=-\frac{3}{4} x\)
\(-\frac{2}{5}=\frac{1}{10} a\)
- Contestar
-
\(a=-4\)
\(-\frac{1}{3} q=-\frac{5}{6}\)
\(-\frac{7}{10} x=-\frac{14}{3}\)
- Contestar
-
\(x=\frac{20}{3}\)
\(\frac{3}{8} y=-\frac{1}{4}\)
\(\frac{7}{12}=-\frac{3}{4} p\)
- Contestar
-
\(p=-\frac{7}{9}\)
\(\frac{11}{18}=-\frac{5}{6} q\)
\(-\frac{5}{18}=-\frac{10}{9} u\)
- Contestar
-
\(u=\frac{1}{4}\)
\(-\frac{7}{20}=-\frac{7}{4} v\)
Resolver ecuaciones que requieren simplificación
En los siguientes ejercicios, resuelve cada ecuación que requiere simplificación.
\(100-16=4 p-10 p-p\)
- Contestar
-
\(p=-12\)
\(-18-7=5 t-9 t-6 t\)
\(\frac{7}{8} n-\frac{3}{4} n=9+2\)
- Contestar
-
\(n=88\)
\(\frac{5}{12} q+\frac{1}{2} q=25-3\)
\(0.25 d+0.10 d=6-0.75\)
- Contestar
-
d=15
\(0.05 p-0.01 p=2+0.24\)
\(-10(q-4)-57=93\)
- Contestar
-
\(q=-11\)
\(-12(d-5)-29=43\)
\(-10(x+4)-19=85\)
- Contestar
-
\(x=-\frac{72}{5}\)
\(-15(z+9)-11=75\)
Práctica Mixta
En los siguientes ejercicios, resuelve cada ecuación.
\(\frac{9}{10} x=90\)
- Contestar
-
\(x=100\)
\(\frac{5}{12} y=60\)
\(y+46=55\)
- Contestar
-
\(y=9\)
\(x+33=41\)
\(\frac{w}{-2}=99\)
- Contestar
-
\(w=-198\)
\(\frac{s}{-3}=-60\)
\(27=6 a\)
- Contestar
-
\(a=\frac{9}{2}\)
\(-a=7\)
\(-x=2\)
- Contestar
-
\(x=-2\)
\(z-16=-59\)
\(m-41=-14\)
- Contestar
-
\(m=27\)
\(0.04 r=52.60\)
\(63.90=0.03 p\)
- Contestar
-
\(p=2130\)
\(-15 x=-120\)
\(84=-12 z\)
- Contestar
-
\(y=-7\)
\(19.36=x-0.2 x\)
\(c-0.3 c=35.70\)
- Contestar
-
\(c=51\)
\(-y=-9\)
\(-x=-8\)
- Contestar
-
\(x=8\)
Traducir a una ecuación y resolver
En los siguientes ejercicios, traduzca a una ecuación y luego resuelva.
187 es el producto de\(-17\) y\(m\)
133 es el producto de\(-19\) y\(n\)
- Contestar
-
\(133=-19 n ; n=-7\)
\(-184\)es el producto de 23 y\(p\)
\(-152\)es el producto de 8 y\(q\)
- Contestar
-
\(-152=8 q ; q=-19\)
\(u\)dividido por 7 es igual a\(-49\)
\(r\)dividido por 12 es igual a\(-48\)
- Contestar
-
\(\frac{r}{12}=-48 ; r=-576\)
\(h\)dividido por\(-13\) es igual a\(-65\)
\(j\)dividido por\(-20\) es igual a\(-80\)
- Contestar
-
\(\frac{j}{-20}=-80 ; j=1,600\)
El cociente\(c\) y\(-19\) es\(38 .\)
El cociente de\(b\) y\(-6\) es 18
- Contestar
-
\(\frac{b}{-6}=18 ; b=-108\)
El cociente de\(h\) y 26 es\(-52\)
El cociente\(k\) y 22 es\(-66\)
- Contestar
-
\(\frac{k}{22}=-66 ; k=-1,452\)
Cinco sextos de\(y\) es 15
Tres décimas de\(x\) es 15
- Contestar
-
\(\frac{3}{10} x=15 ; x=50\)
Cuatro tercios de\(w\) es 36
Cinco mitades de\(v\) es 50
- Contestar
-
\(\frac{5}{2} v=50 ; v=20\)
La suma de nueve décimas y\(g\) es de dos tercios.
La suma de dos quintas partes y\(f\) es la mitad.
- Contestar
-
\(\frac{2}{5}+f=\frac{1}{2} ; f=\frac{1}{10}\)
La diferencia de\(p\) y un sexto es de dos tercios.
La diferencia de\(q\) y un octavo es de tres cuartas partes.
- Contestar
-
\(q-\frac{1}{8}=\frac{3}{4} ; q=\frac{7}{8}\)
Traducir y resolver aplicaciones
En los siguientes ejercicios, traduzca en una ecuación y resuelva.
Kindergarten La clase de kindergarten de Connie tiene 24 niños. Ella quiere que se metan en 4 grupos iguales. ¿Cuántos niños va a poner en cada grupo?
Globos Ramona compró 18 globos para una fiesta. Ella quiere hacer 3 racimos iguales. ¿Cuántos globos usó en cada grupo?
- Contestar
-
6 globos
Boletos Mollie pagó $36.25 por 5 boletos de cine. ¿Cuál era el precio de cada boleto?
Shopping Serena pagó 12.96 dólares por un paquete de 12 pares de calcetines deportivos. ¿Cuál era el precio del par de calcetines deportivos?
- Contestar
-
$1.08
Nancy de costura utilizó 14 yardas de tela para hacer banderas para un tercio del equipo de perforación. ¿Cuánta tela necesitaría Nancy para hacer banderas para todo el equipo?
MPG John's SUV obtiene 18 millas por galón (mpg). Esto es la mitad de mpg que el auto híbrido de su esposa. ¿Cuántas millas por galón obtiene el auto híbrido?
- Contestar
-
36 mpg
Altura Aiden mide 27 pulgadas de alto. Es\(\frac{3}{8}\) tan alto como su padre. ¿Qué tan alto es su padre?
Bienes raíces Bea ganó\(\$ 11,700\) comisión por vender una casa, calculada a partir\(\frac{6}{100}\) del precio de venta. ¿Cuál era el
precio de venta de la casa?
- Contestar
-
$195,000
Matemáticas cotidianas
Comisiones Cada semana se le paga a Perry\(\$150\) más el 12% del monto total de sus ventas. Resuelve la ecuación
\(840=150+0.12(a-1250)\)\(a\) para encontrar la cantidad total que Perry debe vender para que se le pague\(\$ 840\) una semana.
Sellos Travis compró 9.45 dólares en sellos de 49 centavos y sellos de 21 centavos. El número de sellos de 21 centavos fue 5 menos que el número de sellos de 49 centavos. Resuelve la ecuación 0.49s+0.21 (s−5) =9.45 para s, para encontrar el número de sellos de 49 centavos que Travis compró.
- Contestar
-
15 sellos de 49 centavos
Ejercicios de escritura
Frida comenzó a resolver la ecuación −3x=36 sumando 3 a ambos lados. Explique por qué el método de Frida no resolverá la ecuación.
Emiliano piensa que\(x=40\) es la solución a la ecuación\(\frac{1}{2} x=80 .\) Explica por qué se equivoca.
- Contestar
-
Las respuestas variarán.
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
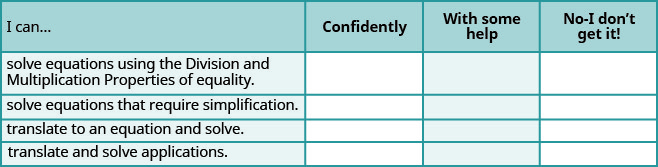
ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


