2.3: Resolver ecuaciones con variables y constantes en ambos lados
- Page ID
- 110237
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Resolver una ecuación con constantes en ambos lados
- Resolver una ecuación con variables en ambos lados
- Resolver una ecuación con variables y constantes en ambos lados
Antes de comenzar, toma este cuestionario de preparación.
- Simplifica: 4y−9+9.
Si te perdiste este problema, revisa Ejercicio 1.10.20.
Resolver ecuaciones con constantes en ambos lados
En todas las ecuaciones que hemos resuelto hasta ahora, todos los términos variables estaban en un solo lado de la ecuación con las constantes en el otro lado. Esto no sucede todo el tiempo, así que ahora aprenderemos a resolver ecuaciones en las que los términos variables, o términos constantes, o ambos están en ambos lados de la ecuación.
Nuestra estrategia implicará elegir un lado de la ecuación para que sea el “lado variable”, y el otro lado de la ecuación para que sea el “lado constante”. Luego, usaremos las Propiedades de Suma y Suma de Igualdad para obtener todos los términos variables juntos en un lado de la ecuación y los términos constantes juntos en el otro lado.
Al hacer esto, transformaremos la ecuación que comenzó con variables y constantes en ambos lados en la forma\(ax=b\). Ya sabemos resolver ecuaciones de esta forma utilizando las Propiedades de División o Multiplicación de Igualdad.
Resolver:\(7x+8=−13\).
- Contestar
-
En esta ecuación, la variable se encuentra únicamente en el lado izquierdo. Tiene sentido llamar al lado izquierdo el lado “variable”. Por lo tanto, el lado derecho será el lado “constante”. Escribiremos las etiquetas encima de la ecuación para ayudarnos a recordar qué va a dónde va.
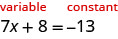
Dado que el lado izquierdo es el “xx”, o lado variable, el 8 está fuera de lugar. Debemos “deshacer” sumando 8 restando 8, y para mantener la igualdad debemos restar 8 de ambos lados.
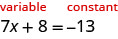
Utilizar la Propiedad de Sustracción de Igualdad.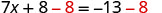 
Simplificar.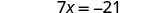 
Ahora todas las variables están a la izquierda y la constante a la derecha. La ecuación se parece a las que aprendiste a resolver antes. Utilizar la División Propiedad de Igualdad.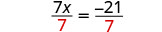 
Simplificar.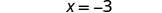 
Comprobar: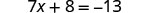 
Deje x=−3.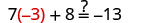 
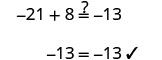
Resolver:\(3x+4=−8\).
- Contestar
-
\(x=−4\)
Resolver:\(5a+3=−37\).
- Contestar
-
\(a=−8\)
Resolver:\(8y−9=31\).
- Contestar
-
Observe que la variable está solo en el lado izquierdo de la ecuación, por lo que llamaremos a este lado el lado “variable”, y el lado derecho será el lado “constante”. Dado que el lado izquierdo es el lado “variable”, el 9 está fuera de lugar. Se resta del 8y, por lo tanto, para “deshacer” la resta, sumar 9 a ambos lados. Recuerda, hagas lo que hagas a la izquierda, debes hacerlo a la derecha.
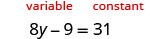
Agrega 9 a ambos lados. 
Simplificar. 
Las variables están ahora en un lado y las constantes en el otro.
Seguimos desde aquí como hicimos antes.Divide ambos lados por 8. 
Simplificar.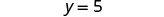 
Comprobar: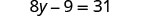 
Dejar y=5.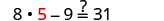 
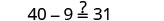
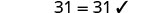
Resolver:\(5y−9=16\).
- Contestar
-
\(y=5\)
Resolver:\(3m−8=19\).
- Contestar
-
\(m = 9\)
Resolver ecuaciones con variables y constantes en ambos lados
El siguiente ejemplo será el primero en tener variables y constantes en ambos lados de la ecuación. Puede tomar varios pasos para resolver esta ecuación, por lo que necesitamos una estrategia clara y organizada.
Resolver:\(9x=8x−6\).
- Contestar
-
Aquí la variable está en ambos lados, pero las constantes sólo aparecen en el lado derecho, así que hagamos del lado derecho el lado “constante”. Entonces el lado izquierdo será el lado “variable”.
No queremos ninguna x a la derecha, así que resta el 8x de ambos lados.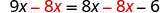 
Simplificar.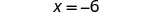 
Logramos obtener las variables en un lado y las constantes por el otro, y hemos obtenido la solución. Comprobar: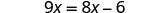 
Deje x=−6.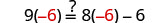 
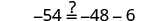
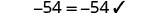
Resolver:\(6n=5n−10\).
- Contestar
-
\(n = -10\)
Resolver:\(-6c = -7c - 1\)
- Contestar
-
\(c = -1\)
Resolver:\(5y - 9 = 8y\)
- Contestar
-
La única constante está a la izquierda y las y están en ambos lados. Dejemos la constante a la izquierda y pongamos las variables a la derecha.
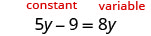
Restar 5y de ambos lados.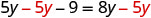 
Simplificar.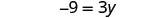 
Tenemos las y a la derecha y las
constantes a la izquierda. Divide ambos lados por 3.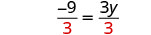
Simplificar.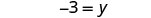 
Comprobar: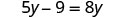 
Vamos\(y=−3\).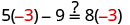 
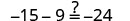
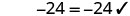
Resolver:\(3p−14=5p\).
- Contestar
-
\(p = -7\)
Resolver:\(8m + 9 = 5m\)
- Contestar
-
\(m = -3\)
Resolver:\(12x = -x + 26\)
- Contestar
-
La única constante está a la derecha, así que deja que el lado izquierdo sea el lado “variable”.
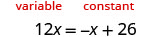
Retire el −x del lado derecho agregando x a ambos lados.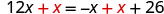 
Simplificar.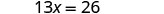 
Todas las x están a la izquierda y las constantes a la derecha. Divide ambos lados por 13.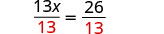 
Simplificar.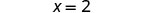 
Resolver:\(12j = -4j + 32\)
- Contestar
-
\(j = 2\)
Resolver:\(8h = -4h + 12\)
- Contestar
-
\(h = 1\)
Resolver ecuaciones con variables y constantes en ambos lados
El siguiente ejemplo será el primero en tener variables y constantes en ambos lados de la ecuación. Puede tomar varios pasos para resolver esta ecuación, por lo que necesitamos una estrategia clara y organizada.
Resolver:\(7x + 5 = 6x + 2\)
- Contestar
-
Resolver:\(12x+8=6x+2\).
- Contestar
-
\(x=−1\)
Resolver:\(9y+4=7y+12\).
- Contestar
-
\(y=4\)
Enumeraremos los pasos a continuación para que pueda consultarlos fácilmente. Pero a esto lo llamaremos la 'Estrategia de inicio' porque iremos agregando algunos pasos más adelante en este capítulo.
- Elige qué lado será el lado “variable”; el otro lado será el lado “constante”.
- Recoger los términos variables al lado “variable” de la ecuación, usando la Propiedad de Suma o Resta de Igualdad.
- Recoge todas las constantes al otro lado de la ecuación, usando la Propiedad de Suma o Resta de Igualdad.
- Hacer que el coeficiente de la variable sea igual a 1, utilizando la Multiplicación o División Propiedad de Igualdad.
- Verifique la solución sustituyéndola en la ecuación original.
En el Paso 1, un enfoque útil es hacer del lado “variable” el lado que tiene la variable con el coeficiente mayor. Esto suele facilitar la aritmética.
Resolver:\(8n−4=−2n+6\).
- Contestar
-
En el primer paso, elija el lado variable comparando los coeficientes de las variables en cada lado.
Ya que\(8>−2\), hacer del lado izquierdo el lado “variable”.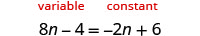 
No queremos términos variables en el lado derecho: agregue 2n a ambos lados para dejar solo constantes a la derecha.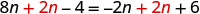 
Combina términos similares.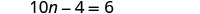 
No queremos ninguna constante en el lado izquierdo, así que agrega 4 a ambos lados.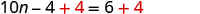 
Simplificar.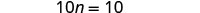 
El término variable está a la izquierda y el término constante está a la derecha. Para que el coeficiente de nn sea uno, divida ambos lados por 10.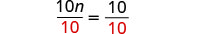 
Simplificar.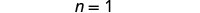 
Comprobar: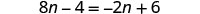 
Dejar n=1.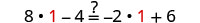 
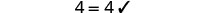
Resolver:\(8q - 5 = -4q + 7\)
- Contestar
-
\(q = 1\)
Resolver:\(7n - 3 = n + 3\)
- Contestar
-
\(n = 1\)
Resolver:\(7a -3 = 13a + 7\)
- Contestar
-
En el primer paso, elija el lado variable comparando los coeficientes de las variables en cada lado.
Desde 13>7, haga del lado derecho el lado “variable” y el lado izquierdo el lado “constante”.
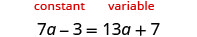
Restar 7a de ambos lados para eliminar el término variable de la izquierda.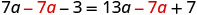 
Combina términos similares.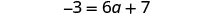 
Restar 7 de ambos lados para eliminar la constante de la derecha.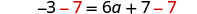 
Simplificar.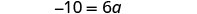 
Divide ambos lados por 6 para que 1 sea el coeficiente de a.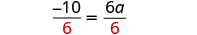 
Simplificar.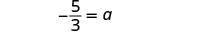 
Comprobar: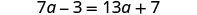 
Vamos\(a=−\frac{5}{3}\).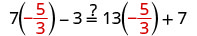 
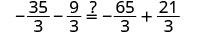
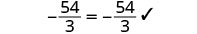
Resolver:\(2a - 2 = 6a + 18\)
- Contestar
-
\(a = -5\)
Resolver:\(4k -1 = 7k + 17\)
- Contestar
-
\(k = -6\)
En el último ejemplo, podríamos haber hecho del lado izquierdo el lado “variable”, pero habría llevado a un coeficiente negativo en el término variable. (¡Pruébalo!) Si bien podríamos trabajar con lo negativo, hay menos posibilidades de errores al trabajar con positivos. ¡La estrategia esbozada anteriormente ayuda a evitar los negativos!
Para resolver una ecuación con fracciones, ¡solo seguimos los pasos de nuestra estrategia para obtener la solución!
Resolver:\(\frac{4}{5}x + 6 = \frac{1}{4}x - 2\)
- Contestar
-
Ya que\(\frac{5}{4} > \frac{1}{4}\), hacer el lado izquierdo el lado “variable” y el lado derecho el lado “constante”.
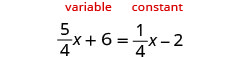
Restar\(\frac{1}{4}x\) de ambos lados.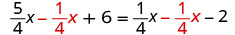 
Combina términos similares.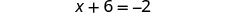 
Restar 6 de ambos lados.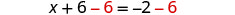 
Simplificar.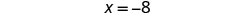 
Comprobar: Let\(x = -8\)
\(\begin{array} {ccc} {\frac{5}{4}x + 6} &{=} &{\frac{1}{4}x - 2} \\ {\frac{5}{4}(-8) + 6} &{\stackrel{?}{=}} &{\frac{1}{4}(-8) - 2} \\ {-10 + 6} &{\stackrel{?}{=}} &{-2 - 2} \\ {-4} &{=} &{-4\checkmark} \end{array}\)
Resolver:\(\frac{7}{8}x - 12 = -\frac{1}{8}x - 2\)
- Contestar
-
\(x = 10\)
Resolver:\(\frac{7}{6}x + 11 = \frac{1}{6}y + 8\)
- Contestar
-
\(y = -3\)
Utilizaremos la misma estrategia para encontrar la solución para una ecuación con decimales.
Resolver:\(7.8x+4=5.4x−8\).
- Contestar
-
Ya que\(7.8>5.4\), hacer el lado izquierdo el lado “variable” y el lado derecho el lado “constante”.
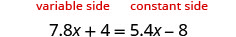
Restar 5.4x de ambos lados.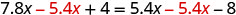 
Combina términos similares.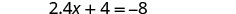 
Restar 4 de ambos lados.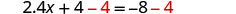 
Simplificar.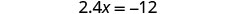 
Utilizar la División Propiedad de Igualdad.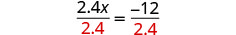 
Simplificar.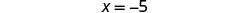 
Comprobar: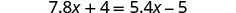 
Let\(x=−5\)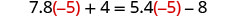 
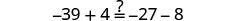
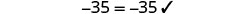
Resolver:\(2.8x + 12 = -1.4x - 9\)
- Contestar
-
\(x = -5\)
Resolver:\(3.6y + 8 = 1.2y - 4\)
- Contestar
-
\(y = -5\)
Conceptos clave
- Estrategia inicial para resolver una ecuación con variables y constantes en ambos lados de la ecuación
- Elige qué lado será el lado “variable”; el otro lado será el lado “constante”.
- Recoger los términos variables al lado “variable” de la ecuación, usando la Propiedad de Suma o Resta de Igualdad.
- Recoge todas las constantes al otro lado de la ecuación, usando la Propiedad de Suma o Resta de Igualdad.
- Hacer que el coeficiente de la variable sea igual a 1, utilizando la Multiplicación o División Propiedad de Igualdad.
- Verifique la solución sustituyéndola en la ecuación original.