2.2: Resolver ecuaciones usando las propiedades de división y multiplicación de la igualdad
- Page ID
- 110251
Al final de esta sección, podrás:
- Resolver ecuaciones usando las Propiedades de División y Multiplicación de Igualdad
- Resolver ecuaciones que requieren simplificación
- Traducir a una ecuación y resolver
- Traducir y resolver aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(−7(\frac{1}{-7})\).
Si te perdiste este problema, revisa el Ejercicio 1.6.13. - Evaluar\(9x+2\) cuándo\(x=−3\).
Si te perdiste este problema, revisa Ejercicio 1.5.34.
Resolver ecuaciones usando las propiedades de división y multiplicación de la igualdad
Te habrás dado cuenta de que todas las ecuaciones que hemos resuelto hasta ahora han sido de la forma\(x+a=b\) o\(x−a=b\). Pudimos aislar la variable sumando o restando el término constante en el lado de la ecuación con la variable. Ahora veremos cómo resolver ecuaciones que tienen una variable multiplicada por una constante y así requerirán división para aislar la variable.
Volvamos a ver nuestro rompecabezas con los sobres y mostradores en Figura\(\PageIndex{1}\).
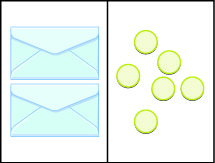
En la ilustración hay dos envolventes idénticos que contienen el mismo número de contadores. Recuerda, el lado izquierdo del espacio de trabajo debe ser igual al lado derecho, pero los contadores del lado izquierdo están “ocultos” en los sobres. Entonces, ¿cuántos contadores hay en cada sobre?
¿Cómo determinamos el número? Tenemos que separar los contadores del lado derecho en dos grupos del mismo tamaño para que se correspondan con los dos sobres del lado izquierdo. Los 6 contadores divididos en 2 grupos iguales dan 3 contadores en cada grupo (desde\(6\div 2=3\)).
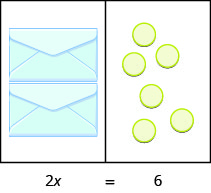
¿Qué ecuación modela la situación mostrada en la Figura\(\PageIndex{2}\)? Hay dos sobres, y cada uno contiene xx contadores. En conjunto, los dos sobres deben contener un total de 6 contadores.
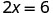 |
|
| Si dividimos ambos lados de la ecuación por 2, como hicimos con los sobres y los contadores, | 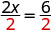 |
| obtenemos: | 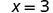 |
Encontramos que cada sobre contiene 3 contadores. ¿Esto comprueba? Lo sabemos\(2\cdot 3=6\), ¡así funciona! ¡Tres contadores en cada uno de dos sobres hace igual a seis!
Este ejemplo lleva a la División Propiedad de la Igualdad.
Para cualquier número a, b y c, y\(c\neq 0\),
\[\begin{array} {llll} {\text { If }} &{a} &{=} &{b} \\ {\text {then}} & {\frac { a } { c }} &{=} &{\frac { b } { c }} \end{array}\]
Cuando divides ambos lados de una ecuación por cualquier número distinto de cero, todavía tienes igualdad.
Hacer la actividad de Matemáticas Manipulativas “División Propiedad de Igualdad” te ayudará a desarrollar una mejor comprensión de cómo resolver ecuaciones mediante el uso de la División Propiedad de Igualdad.
El objetivo al resolver una ecuación es 'deshacer' la operación sobre la variable. En el siguiente ejemplo, la variable se multiplica por 5, por lo que dividiremos ambos lados por 5 para 'deshacer' la multiplicación.
Resolver:\(5x=−27\).
- Contestar
-
Para aislar x, “deshacer” la multiplicación por 5. 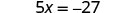
Dividir para 'deshacer' la multiplicación. 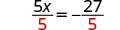
Simplificar. 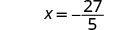
Comprobar: 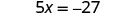
Sustituto\(-\frac{27}{5}\) por x. 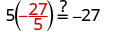
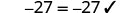
Dado que esta es una verdadera afirmación,\(x = -\frac{27}{5}\)
es la solución a\(5x=−27\).
Resolver:\(3y=−41\).
- Contestar
-
\(y = -\frac{41}{3}\)
Resolver:\(4z=−55\).
- Contestar
-
\(y = -\frac{55}{4}\)
Considera la ecuación\(\frac{x}{4} = 3\). Queremos saber qué número dividido por 4 da 3. Entonces, para “deshacer” la división, necesitaremos multiplicar por 4. La Multiplicación Propiedad de Igualdad nos permitirá hacer esto. Esta propiedad dice que si empezamos con dos cantidades iguales y multiplicamos ambas por el mismo número, los resultados son iguales.
Para cualquier número a, b y c,
\[\begin{array} {llll} {\text {If}} &{a} & {=} &{b} \\ {\text {then}} &{a c} &{=} &{b c} \end{array}\]
Si multiplicas ambos lados de una ecuación por el mismo número, aún tienes igualdad.
Resolver:\(\frac{y}{-7} = -14\)
- Contestar
-
Aquí y se divide por −7. Debemos multiplicar por −7 para aislar y.

Multiplica ambos lados por −7. 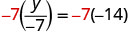
Multiplicar. 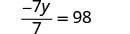
Simplificar. 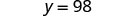
Comprobar:\(\frac{y}{-7} = -14\) Sustituto y=98. 
Dividir. 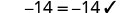
Resolver:\(\frac{a}{-7} = -42\)
- Contestar
-
\(a = 294\)
Resolver:\(\frac{b}{-6} = -24\)
- Contestar
-
\(b = 144\)
Resolver:\(-n = 9\)
- Contestar
-
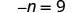
Recuerde que −n es equivalente a −1n. 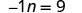
Divide ambos lados por −1. 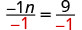
Dividir. 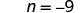
Observe que hay otras dos formas de resolver −n=9. También podemos resolver esta ecuación multiplicando ambos lados por −1 y también tomando lo opuesto de ambos lados. Comprobar: 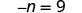
Sustituto n=−9. 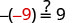
Simplificar. 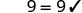
Resolver:\(−k=8\).
- Contestar
-
\(k = -8\)
Resolver:\(−g=3\).
- Contestar
-
\(g = -3\)
Resolver:\(\frac{3}{4}x = 12\)
- Contestar
-
Dado que el producto de un número y su recíproco es 1, nuestra estrategia será aislar x multiplicando por el recíproco de\(\frac{3}{4}\).
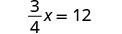
Multiplicar por el recíproco de\(\frac{3}{4}\). 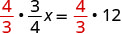
Las reciprocas se multiplican a 1. 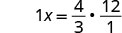
Multiplicar. 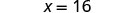
Observe que podríamos haber dividido ambos lados de la ecuación\(\frac{3}{4}x = 12\) por\(\frac{3}{4}\) para aislar x Si bien esto funcionaría, a la mayoría de la gente le resultaría más fácil multiplicar por lo recíproco. Comprobar: 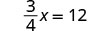
Sustituto\(x=16\). 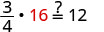
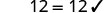
Resolver:\(\frac{2}{5}n=14\).
- Contestar
-
\(n = 35\)
Resolver:\(\frac{5}{6}y=15\).
- Contestar
-
\(y = 18\)
En el siguiente ejemplo, todos los términos variables están en el lado derecho de la ecuación. Como siempre, nuestro objetivo al resolver la ecuación es aislar la variable.
Resolver:\(\frac{8}{15} = -\frac{4}{5}x\)
- Contestar
-
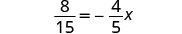
Multiplicar por el recíproco de\(-\frac{4}{5}\). 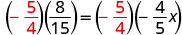
Las reciprocas se multiplican a 1. 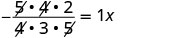
Multiplicar. 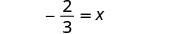
Comprobar: 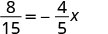
Vamos\(x = -\frac{2}{3}\). 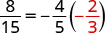
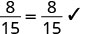
Resolver:\(\frac{9}{25} = -\frac{4}{5}z\)
- Contestar
-
\(z = - \frac{9}{5}\)
\(\frac{5}{6} = -\frac{8}{3}r\)
- Contestar
-
\(r = -\frac{5}{16}\)
Resolver ecuaciones que requieren simplificación
Muchas ecuaciones empiezan más complicadas que las con las que hemos estado trabajando.
Con estas ecuaciones más complicadas el primer paso es simplificar ambos lados de la ecuación tanto como sea posible. Esto generalmente implica combinar términos similares o usar la propiedad distributiva.
Resolver:\(14−23=12y−4y−5y\).
- Contestar
-
Comience simplificando cada lado de la ecuación.
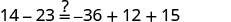
Simplifica cada lado. 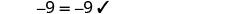
Divide ambos lados por 3 para aislar y. 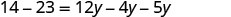
Dividir. 
Comprobar: 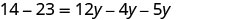
Sustituto\(y=−3\). 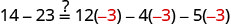
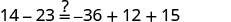
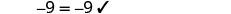
Resolver:\(18−27=15c−9c−3c\).
- Contestar
-
\(c=−3\)
Resolver:\(18−22=12x−x−4x\).
- Contestar
-
\(x = -\frac{4}{7}\)
Resolver:\(−4(a−3)−7=25\).
- Contestar
-
Aquí simplificaremos cada lado de la ecuación usando primero la propiedad distributiva.
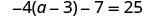
Distribuir. 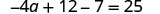
Simplificar. 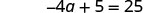
Simplificar. 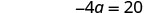
Divide ambos lados por\(-4\) para aislar a. 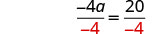
Dividir. 
Comprobar: 
Sustituto\(a = -5\) 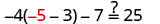
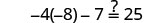
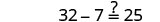
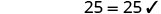
Resolver:\(−4(q−2)−8=24\).
- Contestar
-
\(q=−6\)
Resolver:\(−6(r−2)−12=30\).
- Contestar
-
\(r=−5\)
Ahora hemos cubierto las cuatro propiedades de igualdad: resta, suma, división y multiplicación. Los enumeraremos todos juntos aquí para una fácil referencia.
Cuando sumas, restas, multiplicas o divides la misma cantidad de ambos lados de una ecuación, todavía tienes igualdad.
\ [\ begin {array} {ll} {\ textbf {Propiedad de resta de igualdad}} & {\ textbf {Propiedad de suma de igualdad}}\\
{\ text {Para cualquier número real a, b y c,}} & {\ text {Para cualquier número real a, b y c,}}\\ {
\ text {if} a = b,} & {\ text {if} a = b,} & {\ text {if} = b,}
\\\ {\ texto {entonces} a - c = b - c} & {\ text {then} a + c = b + c}
\\ {\ textbf {Propiedad de división de igualdad}} & {\ textbf {Propiedad de multiplicación de la igualdad}}\\
{\ text {Para cualquier número real a, b y c,}} & {\ text {Para cualquier número real a, b y c,}
\\ {\ text {si} a = b,} & {\ texto {si} a = b,}
\\ {\ texto {entonces} a - c = b - c} & {\ texto {entonces} a + c = b + c}
\ end {array}\]
Cuando sumas, restas, multiplicas o divides la misma cantidad de ambos lados de una ecuación, todavía tienes igualdad.
Traducir a una ecuación y resolver
En los siguientes ejemplos, traduciremos oraciones en ecuaciones y luego resolveremos las ecuaciones. Es posible que desee revisar la tabla de traducciones en el capítulo anterior.
Traducir y resolver: El número 143 es producto de −11 e y.
- Contestar
-
Traducir. 
Dividir por −11. 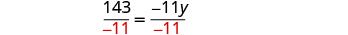
Simplificar. 
Comprobar:
\[\begin{array} {lll} {143} &{=} &{-11y} \\ {143} &{\stackrel{?}{=}} &{-11(-13)} \\ {143} &{=} &{143\checkmark} \end{array}\]
Traducir y resolver: El número 132 es producto de −12 e y.
- Contestar
-
132=−12y; y=−11
Traducir y resolver: El número 117 es el producto de −13 y z.
- Contestar
-
117=−13z; z=−9
Traducir y resolver: n dividido por 8 es −32.
- Contestar
-
Comience traduciendo la oración en una ecuación.
Traducir.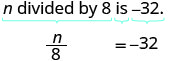
Múltiples ambos lados por 8. 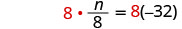
Simplificar. 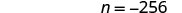
Comprobar: ¿Nn dividido por 8 es igual a −32? Vamos\(n=−256\). ¿−256 dividido por 88 es igual a −32? Traducir. \(\frac{-256}{8} \stackrel{?}{=} -32\) Simplificar. \(−32=−32\checkmark\)
Traducir y resolver: nn dividido por 7 es igual a −21.
- Contestar
-
\(\frac{n}{7}=−21; n=−147\)
Traducir y resolver: n dividido por 8 es igual a −56.
- Contestar
-
\(\frac{n}{8}=−56;n=−448\)
Traducir y resolver: El cociente de yy y −4 es 68.
- Contestar
-
Comience traduciendo la oración en una ecuación.
Traducir. 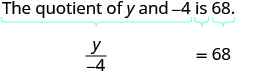
Multiplica ambos lados por -4. 
Simplificar. 
Comprobar: ¿El cociente de y y −4 es igual a 68? Dejar y=−272. ¿El cociente de −272 y −4 es igual a 68? Traducir. \(\frac{-272}{-4} \stackrel{?}{=} 68\) Simplificar. \(68 = 68\checkmark\)
Traducir y resolver: El cociente de q y −8 es 72.
- Contestar
-
\(\frac{q}{-8}=72;q=−576\)
Traducir y resolver: El cociente de p y −9 es 81.
- Contestar
-
\(\frac{p}{-9}=81;p=−729\)
Traducir y resolver: Tres cuartas partes de p es 18.
- Contestar
-
Comience traduciendo la oración en una ecuación. Recuerda, “de” se traduce en multiplicación.
Traducir. 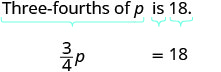
Multiplica ambos lados por\(\frac{4}{3}\). 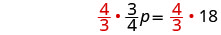
Simplificar. 
Comprobar: ¿Las tres cuartas partes de p son iguales a 18? Dejar p = 24. ¿Tres cuartos de 24 son iguales a 18? Traducir. \(\frac{3}{4}\cdot 24 \stackrel{?}{=} 18\) Simplificar. \(18=18\checkmark\)
Traducir y resolver: Dos quintas partes de f es 16.
- Contestar
-
\(\frac{2}{5}f=16; f=40\)
Traducir y resolver: Tres cuartas partes de f es 21.
- Contestar
-
\(\frac{3}{4}f=21; f=28\)
Traducir y resolver: La suma de tres octavos y x es la mitad.
- Contestar
-
Comience traduciendo la oración en una ecuación.
Traducir. 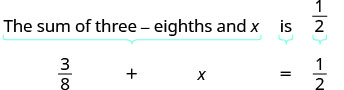
Restar\(\frac{3}{8}\) de cada lado. 
Simplificar y reescribir fracciones con denominadores comunes. 
Simplificar. 
Comprobar: ¿La suma de tres octavos y x es igual a la mitad? Vamos\(x=\frac{1}{8}\). ¿La suma de tres octavos y un octavo es igual a la mitad? Traducir. \(\frac{3}{8} + \frac{1}{8} \stackrel{?}{=} \frac{1}{2}\) Simplificar. \(\frac{4}{8} \stackrel{?}{=} \frac{1}{2}\) Simplificar. \(\frac{1}{2} = \frac{1}{2} \checkmark\)
Traducir y resolver: La suma de cinco octavos y x es una cuarta parte.
- Contestar
-
\(\frac{5}{8} + x = \frac{1}{4}; x = -\frac{3}{8}\)
Traducir y resolver: La suma de tres cuartos y x es de cinco sextos.
- Contestar
-
\(\frac{3}{4} + x = \frac{5}{6}; x = \frac{1}{12}\)
Traducir y resolver aplicaciones
Para resolver aplicaciones usando las Propiedades de División y Multiplicación de Igualdad, seguiremos los mismos pasos que usamos en la última sección. Replantaremos el problema en una sola oración, asignaremos una variable, y luego traduciremos la oración en una ecuación para resolverla.
Denae compró 6 libras de uvas por $10.74. ¿Cuál era el costo de una libra de uvas?
- Contestar
-
\[\begin{array} {ll} {\text{What are you asked to find?}} &{\text{The cost of 1 pound of grapes}} \\\\ {\text{Assign a variable.}} &{\text{Let c = the cost of one pound.}} \\\\ {\text{Write a sentence that gives the}} &{\text{The cost of 6 pounds is }$10.74} \\ {\text{information to find it.}} &{} \\\\ {\text{Translate into an equation.}} &{6c = 10.74} \\ {\text{Solve.}} &{\frac{6c}{c} = \frac{10.74}{6}} \\ {} &{c = 1.79} \\\\ {} &{\text{The grapes cost }$ 1.79 \text{ per pound.}} \\ \\ {\text{Check: If one pound costs }$1.79, do} &{} \\ {\text{6 pounds cost }$ 10.74?} &{} \\\\ {6(1.79) \stackrel{?}{=} 10.74} &{} \\ {10.74 = 10.74\checkmark} &{} \end{array}\]
Traducir y resolver:
Arianna compró un paquete de 24 botellas de agua por $9.36. ¿Cuál era el costo de una botella de agua?
- Contestar
-
$0.39
Traducir y resolver:
En JB's Bowling Alley, 6 personas pueden jugar en un carril por $34.98. ¿Cuál es el costo para cada persona?
- Contestar
-
$5.83
Andreas compró un auto usado por $12,000. Debido a que el auto tenía 4 años de antigüedad, su precio era\(\frac{3}{4}\) del precio original, cuando el auto era nuevo. ¿Cuál era el precio original del auto?
- Contestar
-
\[\begin{array} {ll} {\text{What are you asked to find?}} &{\text{The original price of the car}} \\\\ {\text{Assign a variable.}} &{\text{Let p = the original price.}} \\\\ {\text{Write a sentence that gives the}} &{$12000\text{ is }\frac{3}{4} \text{ of the original price.}} \\ {\text{information to find it.}} &{} \\\\ {\text{Translate into an equation.}} &{12000 = \frac{3}{4}p} \\ {} &{\frac{3}{4}(12000) = \frac{4}{3}\cdot \frac{3}{4}p}\\ {}&{16000 = p} \\{\text{Solve.}} &{} \\\\ {} &{\text{The original cost of the car was }$ 16000.} \\ \\ {\text{Check: Is }\frac{3}{4} \text{ of }$16000 \text{ equal to }$12000} &{} \\\\ {\frac{3}{4}\cdot 16000 \stackrel{?}{=} 12000} &{} \\ {12000 = 12000\checkmark} &{} \end{array}\]
Traducir y resolver:
El impuesto patrimonial anual sobre la casa de Mehta es de $1,800, calculado a partir\(\frac{15}{1000}\) del valor tasado de la casa. ¿Cuál es el valor tasado de la casa de Mehta?
- Contestar
-
$120000
Traducir y resolver:
Stella plantó 14 pisos de flores en\(\frac{2}{3}\) su jardín. ¿Cuántos pisos de flores necesitaría para llenar todo el jardín?
- Contestar
-
21 pisos
Conceptos clave
- La División Propiedad de Igualdad —Para cualquier número a, b, y c, y\(c\neq 0\), si\(a=b\), entonces\(\frac{a}{c} = \frac{b}{c}\).
Cuando divides ambos lados de una ecuación por cualquier número distinto de cero, todavía tienes igualdad. - La propiedad de multiplicación de la igualdad —Para cualquier número a, b, y c, si\(a=b\), entonces\(ac = bc\).
Si multiplicas ambos lados de una ecuación por el mismo número, aún tienes igualdad.


