2.5: Resolver ecuaciones con fracciones o decimales
- Page ID
- 110258
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Resolver ecuaciones con coeficientes de fracción
- Resolver ecuaciones con coeficientes decimales
Antes de comenzar, toma este cuestionario de preparación.
- Multiplicar:\(8\cdot 38\).
Si te perdiste este problema, revisa el Ejercicio 1.6.16. - Encuentra la pantalla LCD de\(\frac{5}{6}\) y\(\frac{1}{4}\).
Si te perdiste este problema, revisa el Ejercicio 1.7.16. - Multiplica 4.78 por 100.
Si te perdiste este problema, revisa Ejercicio 1.8.22.
Resolver ecuaciones con coeficientes de fracción
Usemos la estrategia general para resolver ecuaciones lineales introducidas anteriormente para resolver la ecuación,\(\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}\).
 |
|
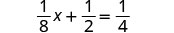| Para aislar el término x, restar\(\frac{1}{2}\) de ambos lados. |  |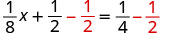
| Simplifica el lado izquierdo. |  |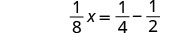
| Cambie las constantes a fracciones equivalentes con la LCD. |  |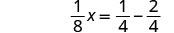
| Resta. |  |
| Multiplicar ambos lados por el recíproco de\(\frac{1}{8}\). |  |
| Simplificar. |  |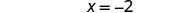
Este método funcionó bien, pero muchos estudiantes no se sienten muy seguros cuando ven todas esas fracciones. Entonces, vamos a mostrar un método alternativo para resolver ecuaciones con fracciones. Este método alternativo elimina las fracciones.
Aplicaremos la Propiedad de Multiplicación de Igualdad y multiplicaremos ambos lados de una ecuación por el mínimo denominador común de todas las fracciones de la ecuación. El resultado de esta operación será una nueva ecuación, equivalente a la primera, pero sin fracciones. A este proceso se le llama “borrar” la ecuación de fracciones.
Vamos a resolver una ecuación similar, pero esta vez usa el método que elimina las fracciones.
Resolver:\(\frac{1}{6}y - \frac{1}{3} = \frac{5}{6}\)
Contestar
Resolver:\(\frac{1}{4}x + \frac{1}{2} = \frac{5}{8}\)
- Contestar
-
\(x= \frac{1}{2}\)
Resolver:\(\frac{1}{8}x + \frac{1}{2} = \frac{1}{4}\)
- Contestar
-
\(x = -2\)
Observe en Ejercicio\(\PageIndex{1}\), una vez que aclaramos la ecuación de fracciones, la ecuación fue como las que resolvimos anteriormente en este capítulo. ¡Cambiamos el problema a uno que ya sabíamos resolver! Luego se utilizó la Estrategia General para Resolver Ecuaciones Lineales.
- Encuentra el mínimo denominador común de todas las fracciones en la ecuación.
- Multiplica ambos lados de la ecuación por esa LCD. Esto borra las fracciones.
- Resuelve usando la Estrategia General para Resolver Ecuaciones Lineales.
Resolver:\(6 = \frac{1}{2}v + \frac{2}{5}v - \frac{3}{4}v\)
- Contestar
-
Queremos borrar las fracciones multiplicando ambos lados de la ecuación por la LCD de todas las fracciones de la ecuación.
Encuentra el LCD de todas las fracciones en la ecuación.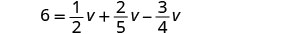 
El LCD es 20. Multiplica ambos lados de la ecuación por 20. 
Distribuir.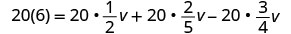 
Simplifica: ¡fíjate, no más fracciones!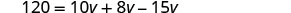 
Combina términos similares. 
Dividir por 3. 
Simplificar. 
Comprobar: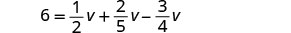 
Dejar v=40.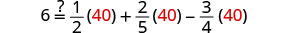 
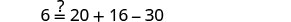
Resolver:\(7 = \frac{1}{2}x + \frac{3}{4}x - \frac{2}{3}x\)
- Contestar
-
\(x = 12\)
Resolver:\(-1 = \frac{1}{2}u + \frac{1}{4}u - \frac{2}{3}u\)
- Contestar
-
\(u = -12\)
En el siguiente ejemplo, nuevamente tenemos variables en ambos lados de la ecuación.
Resolver:\(a + \frac{3}{4} = \frac{3}{8}a - \frac{1}{2}\)
- Contestar
-
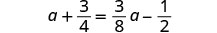
Encuentra la pantalla LCD de todas las fracciones en la ecuación.
El LCD es 8.Multiplica ambos lados por la pantalla LCD.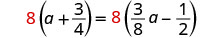 
Distribuir.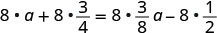 
Simplificar: no más fracciones.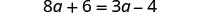 
Restar 3a3a de ambos lados.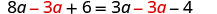 
Simplificar.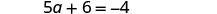 
Restar 6 de ambos lados.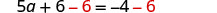 
Simplificar.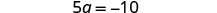 
Dividir por 5.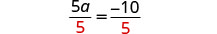 
Simplificar.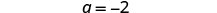 
Comprobar: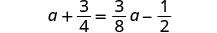 
Deje a=−2.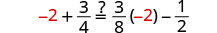 
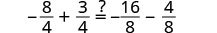
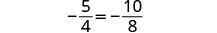
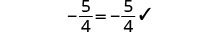
Resolver:\(x + \frac{1}{3} = \frac{1}{6}x - \frac{1}{2}\)
- Contestar
-
\(x = -1\)
Resolver:\(c + \frac{3}{4} = \frac{1}{2}c - \frac{1}{4}\)
- Contestar
-
\(c = -2\)
En el siguiente ejemplo, comenzamos por usar la Propiedad Distributiva. Este paso despeja las fracciones de inmediato.
Resolver:\(-5 = \frac{1}{4}(8x + 4)\)
- Contestar
-
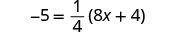
Distribuir.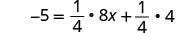 
Simplificar.
Ahora no hay fracciones.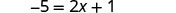
Restar 1 de ambos lados.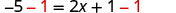 
Simplificar.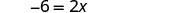 
Dividir por 2.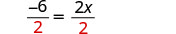 
Simplificar. 
Comprobar: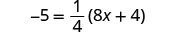 
Deje x=−3.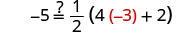 
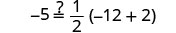
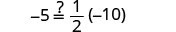
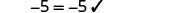
Resolver:\(-11 = \frac{1}{2}(6p + 2)\)
- Contestar
-
\(p = -4\)
Resolver:\(8 = \frac{1}{3}(9q + 6)\)
- Contestar
-
\(q = 2\)
En el siguiente ejemplo, incluso después de distribuir, todavía tenemos fracciones que despejar.
Resolver:\(\frac{1}{2}(y - 5) = \frac{1}{4}(y - 1)\)
- Contestar
-
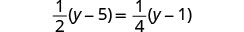
Distribuir.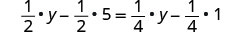 
Simplificar.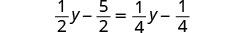 
Multiplicar por la pantalla LCD, 4.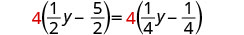 
Distribuir.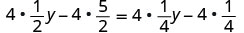 
Simplificar. 
Recoge las variables a la izquierda.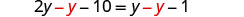 
Simplificar. 
Recoge las constantes a la derecha.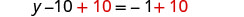 
Simplificar.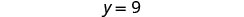 
Comprobar: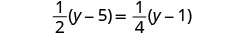 
Dejar y=9.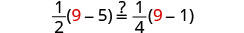 
Termina el cheque por tu cuenta.
Resolver:\(\frac{1}{5}(n + 3) = \frac{1}{4}(n + 2)\)
- Contestar
-
\(n = 2\)
Resolver:\(\frac{1}{2}(m - 3) = \frac{1}{4}(m - 7)\)
- Contestar
-
\(m = -1\)
Resolver:\(\frac{5x - 3}{4} = \frac{x}{2}\)
- Contestar
-
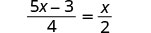
Multiplicar por la pantalla LCD, 4.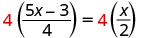 
Simplificar.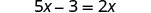 
Recoge las variables a la derecha.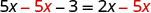 
Simplificar.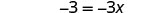 
Dividir.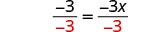 
Simplificar.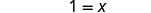 
Comprobar: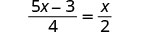 
Dejar x=1.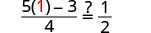 
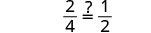
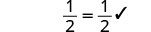
Resolver:\(\frac{4y - 7}{3} = \frac{y}{6}\)
- Contestar
-
\(y = 2\)
Resolver:\(\frac{-2z - 5}{4} = \frac{z}{8}\)
- Contestar
-
\(z = -2\)
Resolver:\(\frac{a}{6} + 2 = \frac{a}{4} + 3\)
- Contestar
-
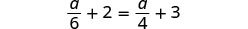
Multiplicar por la pantalla LCD, 12.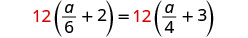 
Distribuir.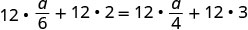 
Simplificar.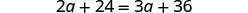 
Recoge las variables a la derecha.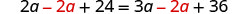 
Simplificar.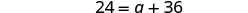 
Recoge las constantes a la izquierda.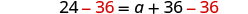 
Simplificar.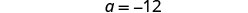 
Comprobar: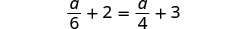 
Deje a=−12.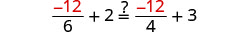 
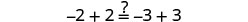
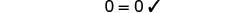
Resolver:\(\frac{b}{10} + 2 = \frac{b}{4} + 5\)
- Contestar
-
\(b = -20\)
Resolver:\(\frac{c}{6} + 3 = \frac{c}{3} + 4\)
- Contestar
-
\(c= -6\)
Resolver:\(\frac{4q + 3}{2}+ 6 = \frac{3q + 5}{4}\)
- Contestar
-
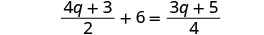
Multiplicar por la pantalla LCD, 4.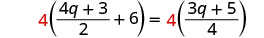 
Distribuir.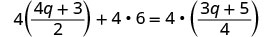 
Simplificar.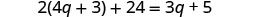 
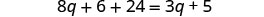
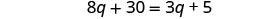
Recoge las variables a la izquierda.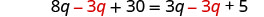 
Simplificar.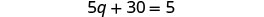 
Recoge las constantes a la derecha. 
Simplificar.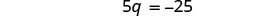 
Dividir por 5.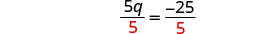 
Simplificar.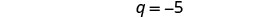 
Comprobar: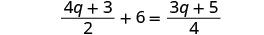 
Deje q = −5.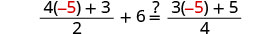 
Termina el cheque por tu cuenta.
Resolver:\(\frac{3r + 5}{6}+ 1 = \frac{4r + 3}{3}\)
- Contestar
-
\(r = 1\)
Resolver:\(\frac{2s + 3}{2}+ 1 = \frac{3s + 2}{4}\)
- Contestar
-
\(s = -8\)
Resolver ecuaciones con coeficientes decimales
Algunas ecuaciones tienen decimales en ellas. Este tipo de ecuaciones ocurrirá cuando resolvamos problemas relacionados con el dinero o los porcentajes. Pero los decimales también se pueden expresar como fracciones. Por ejemplo,\(0.3 = \frac{3}{10}\) y\(0.17 = \frac{17}{100}\). Entonces, con una ecuación con decimales, podemos usar el mismo método que usamos para borrar fracciones, multiplicar ambos lados de la ecuación por el mínimo denominador común.
Resolver:\(0.06x + 0.02 = 0.25x - 1.5\)
- Contestar
-
Mira los decimales y piensa en las fracciones equivalentes.
\(0.06 = \frac { 6 } { 100 } \quad 0.02 = \frac { 2 } { 100 } \quad 0.25 = \frac { 25 } { 100 } \quad 1.5 = 1 \frac { 5 } { 10 }\)
Observe, la pantalla LCD es de 100.
Al multiplicar por la LCD, borraremos los decimales de la ecuación.
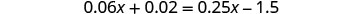
Multiplique ambos lados por 100.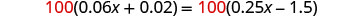 
Distribuir.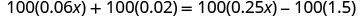 
Multiplicar, y ahora ya no tenemos más decimales.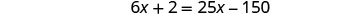 
Recoge las variables a la derecha.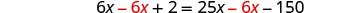 
Simplificar.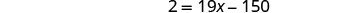 
Recoge las variables a la derecha.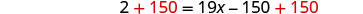 
Simplificar.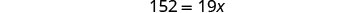 
Dividir por 19.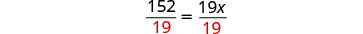 
Simplificar.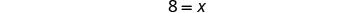 
Comprobar: Let x=8
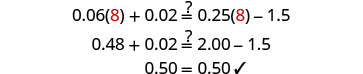
Resolver:\(0.14h + 0.12 = 0.35h - 2.4\)
- Contestar
-
\(h = 12\)
Resolver:\(0.65k - 0.1 = 0.4k - 0.35\)
- Contestar
-
\(k = -1\)
El siguiente ejemplo utiliza una ecuación que es típica de las aplicaciones monetarias en el siguiente capítulo. Observe que distribuimos el decimal antes de borrar todos los decimales.
Resolver:\(0.25x + 0.05(x + 3) = 2.85\)
- Contestar
-
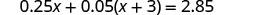
Distribuir primero.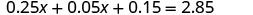 
Combina términos similares.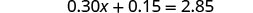 
Para borrar decimales, multiplica por 100.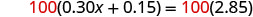 
Distribuir.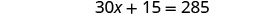 
Restar 15 de ambos lados. 
Simplificar.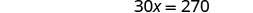 
Dividir por 30.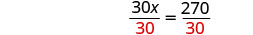 
Simplificar. 
Compruébalo tú mismo sustituyendo x=9 en la ecuación original.
Resolver:\(0.25n + 0.05(n + 5) = 2.95\)
- Contestar
-
\(n = 9\)
Resolver:\(0.10d + 0.05(d -5) = 2.15\)
- Contestar
-
\(d = 16\)
Conceptos clave
- Estrategia para resolver una ecuación con coeficientes de fracción
- Encuentra el mínimo denominador común de todas las fracciones en la ecuación.
- Multiplica ambos lados de la ecuación por esa LCD. Esto borra las fracciones.
- Resuelve usando la Estrategia General para Resolver Ecuaciones Lineales.