5.1: Resolver sistemas de ecuaciones mediante gráficos
- Page ID
- 110173
Al final de esta sección, podrás:
- Determinar si un par ordenado es una solución de un sistema de ecuaciones
- Resolver un sistema de ecuaciones lineales graficando
- Determinar el número de soluciones de sistema lineal
- Resolver aplicaciones de sistemas de ecuaciones graficando
Antes de comenzar, toma este cuestionario de preparación.
- Para la ecuación\(y=\frac{2}{3}x−4\)
ⓐ ¿es (6,0) una solución? ⓑ es (−3, −2) una solución?
Si te perdiste este problema, revisa el Ejercicio 2.1.1. - Encuentra la pendiente y la intersección en y de la línea 3x−y=12.
Si te perdiste este problema, revisa el Ejercicio 4.5.7. - Encuentra las intercepciones x e y de la línea 2x−3y=12.
Si te perdiste este problema, revisa el Ejercicio 4.3.7.
Determinar si un par ordenado es una solución de un sistema de ecuaciones
En la sección de Resolver ecuaciones lineales y desigualdades aprendimos a resolver ecuaciones lineales con una variable. Recuerde que la solución de una ecuación es un valor de la variable que hace una declaración verdadera cuando se sustituye en la ecuación. Ahora trabajaremos con sistemas de ecuaciones lineales, dos o más ecuaciones lineales agrupadas.
Cuando se agrupan dos o más ecuaciones lineales, forman un sistema de ecuaciones lineales.
Enfocaremos nuestro trabajo aquí en sistemas de dos ecuaciones lineales en dos incógnitas. Posteriormente, se pueden resolver sistemas de ecuaciones más grandes.
A continuación se muestra un ejemplo de un sistema de dos ecuaciones lineales. Utilizamos un corsé para mostrar que las dos ecuaciones se agrupan para formar un sistema de ecuaciones.
\[\begin{cases}{2 x+y=7} \\ {x-2 y=6}\end{cases}\]
Una ecuación lineal en dos variables, como 2 x + y = 7, tiene un número infinito de soluciones. Su gráfica es una línea. Recuerde, cada punto de la línea es una solución a la ecuación y cada solución a la ecuación es un punto en la línea.
Para resolver un sistema de dos ecuaciones lineales, queremos encontrar los valores de las variables que son soluciones a ambas ecuaciones. Es decir, estamos buscando los pares ordenados (x, y) que hagan verdaderas ambas ecuaciones. A estas se les llama las soluciones a un sistema de ecuaciones.
Las soluciones de un sistema de ecuaciones son los valores de las variables que hacen verdaderas todas las ecuaciones. Una solución de un sistema de dos ecuaciones lineales está representada por un par ordenado (x, y).
Para determinar si un par ordenado es una solución a un sistema de dos ecuaciones, sustituimos los valores de las variables en cada ecuación. Si el par ordenado hace que ambas ecuaciones sean verdaderas, es una solución para el sistema.
Consideremos el sistema a continuación:
\[\begin{cases}{3x−y=7} \\ {x−2y=4}\end{cases}\]
¿El par ordenado (2, −1) es una solución?
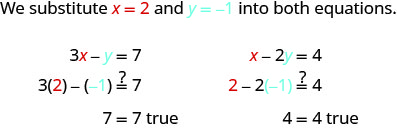
El par ordenado (2, −1) hizo que ambas ecuaciones fueran verdaderas. Por lo tanto (2, −1) es una solución a este sistema.
Probemos con otro par ordenado. ¿El par ordenado (3, 2) es una solución?
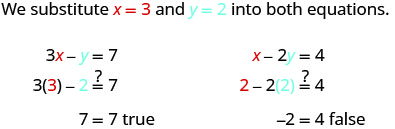
El par ordenado (3, 2) hizo cierta una ecuación, pero hizo falsa la otra ecuación. Al no ser una solución a ambas ecuaciones, no es una solución a este sistema.
Determine si el par ordenado es una solución para el sistema:\(\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}\)
- (−2, −1)
- (−4, −3)
- Contestar
-
1.
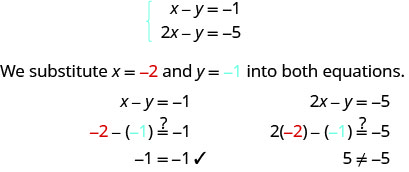
(−2, −1) no hace que ambas ecuaciones sean verdaderas. (−2, −1) no es una solución.
2.
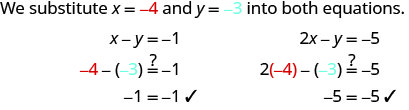
(−4, −3) no hace que ambas ecuaciones sean verdaderas. (−4, −3) es una solución.
Determine si el par ordenado es una solución para el sistema:\(\begin{cases}{3x+y=0} \\ {x+2y=−5}\end{cases}\)
- (1, −3)
- (0,0)
- Contestar
-
- si
- no
Determine si el par ordenado es una solución para el sistema:\(\begin{cases}{x−3y=−8} \\ {−3x−y=4}\end{cases}\)
- (2, −2)
- (−2,2)
- Contestar
-
- no
- si
Resolver un Sistema de Ecuaciones Lineales por Grafiación
En este capítulo utilizaremos tres métodos para resolver un sistema de ecuaciones lineales. El primer método que usaremos es graficar. La gráfica de una ecuación lineal es una línea. Cada punto de la línea es una solución a la ecuación. Para un sistema de dos ecuaciones, vamos a graficar dos líneas. Entonces podemos ver todos los puntos que son soluciones a cada ecuación. Y, al encontrar lo que tienen en común las líneas, encontraremos la solución al sistema.
La mayoría de las ecuaciones lineales en una variable tienen una solución, pero vimos que algunas ecuaciones, llamadas contradicciones, no tienen soluciones y para otras ecuaciones, llamadas identidades, todos los números son soluciones. De igual manera, cuando resolvemos un sistema de dos ecuaciones lineales representadas por una gráfica de dos líneas en un mismo plano, hay tres casos posibles, como se muestra en la Figura\(\PageIndex{1}\):
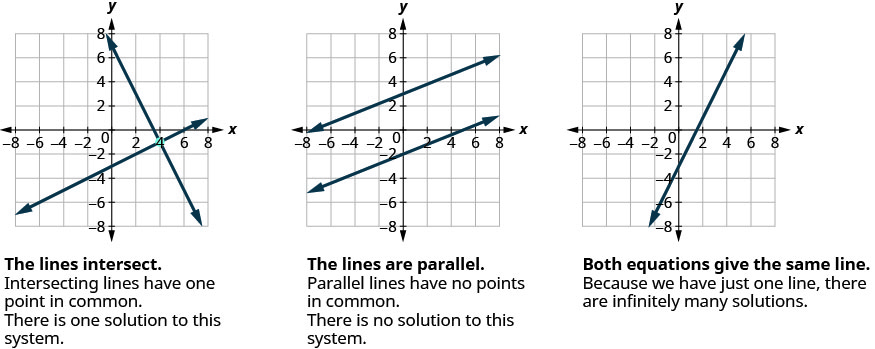
Para el primer ejemplo de resolver un sistema de ecuaciones lineales en esta sección y en las dos secciones siguientes, resolveremos el mismo sistema de dos ecuaciones lineales. Pero usaremos un método diferente en cada sección. Después de ver el tercer método, decidirás cuál fue el método más conveniente para resolver este sistema.
Resuelve el sistema graficando:\(\begin{cases}{2x+y=7} \\ {x−2y=6}\end{cases}\)
- Contestar
-
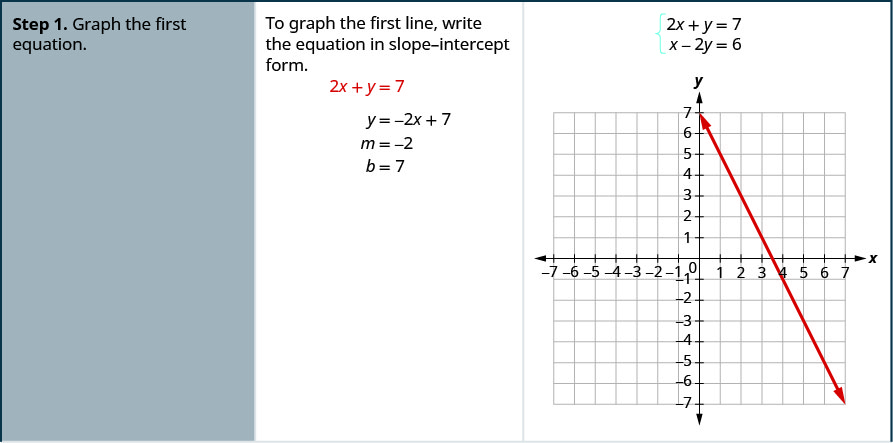
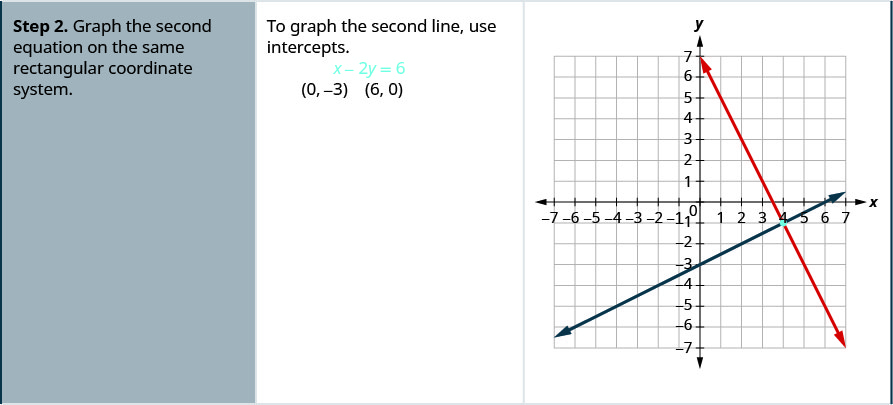


Resuelve cada sistema graficando:\(\begin{cases}{x−3y=−3} \\ {x+y=5}\end{cases}\)
- Contestar
-
(3,2)
Resuelve cada sistema graficando:\(\begin{cases}{−x+y=1} \\ {3x+2y=12}\end{cases}\)
- Contestar
-
(2,3)
A continuación se muestran los pasos a utilizar para resolver un sistema de ecuaciones lineales mediante la gráfica.
- Grafica la primera ecuación.
- Grafique la segunda ecuación en el mismo sistema de coordenadas rectangulares.
- Determine si las líneas se cruzan, son paralelas o son la misma línea.
- Identificar la solución al sistema.
- Si las líneas se cruzan, identifique el punto de intersección. Verifique para asegurarse de que sea una solución a ambas ecuaciones. Esta es la solución al sistema.
- Si las líneas son paralelas, el sistema no tiene solución.
- Si las líneas son las mismas, el sistema tiene un número infinito de soluciones.
Resuelve el sistema graficando:\(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)
- Contestar
-
Ambas ecuaciones en este sistema están en forma de pendiente-intersección, por lo que usaremos sus pendientes e intercepciones y para graficarlas. \(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)
Encuentra la pendiente y -intercepción de la
primera ecuación.
Encuentra la pendiente y -intercepción de la
primera ecuación.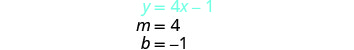
Grafica las dos líneas. Determinar el punto de intersección. Las líneas se cruzan en (1, 3). 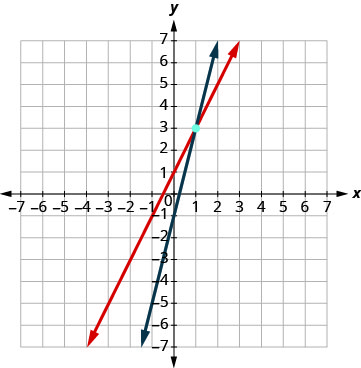
Verifique la solución en ambas ecuaciones. \(\begin{array}{l}{y=2 x+1} & {y = 4x - 1}\\{3\stackrel{?}{=}2 \cdot 1+1} &{3\stackrel{?}{=}4 \cdot 1-1} \\ {3=3 \checkmark}&{3=3 \checkmark} \end{array}\) La solución es (1, 3).
Resuelve el sistema graficando:\(\begin{cases}{y=2x+2} \\ {y=-x−4}\end{cases}\)
- Contestar
-
(−2, −2)
Resuelve el sistema graficando:\(\begin{cases}{y=3x+3} \\ {y=-x+7}\end{cases}\)
- Contestar
-
(1,6)
Ambas ecuaciones en Ejercicio\(\PageIndex{7}\) se dieron en forma de pendiente-intercepción. Esto nos facilitó graficar rápidamente las líneas. En el siguiente ejemplo, primero volveremos a escribir las ecuaciones en forma pendiente-interceptar.
Resuelve el sistema graficando:\(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)
- Contestar
-
Resolveremos ambas ecuaciones para yy para que podamos graficarlas fácilmente usando sus pendientes e intercepciones y. \(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)
Resuelve la primera ecuación para y.
Encuentra la pendiente y -intercepción.
Resuelve la segunda ecuación para y.
Encuentra la pendiente y -intercepción.\(\begin{aligned} 3 x+y &=-1 \\ y &=-3 x-1 \\ m &=-3 \\ b &=-1 \\ 2 x+y &=0 \\ y &=-2 x \\ b &=0 \end{aligned}\) Grafica las líneas. 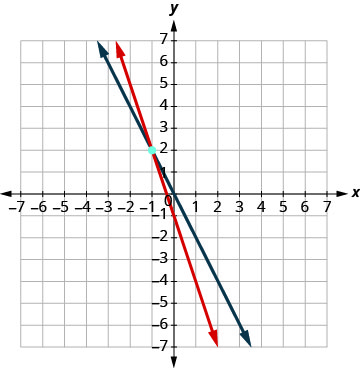
Determinar el punto de intersección. Las líneas se cruzan en (−1, 2). Verifique la solución en ambas ecuaciones. \(\begin{array}{rllrll}{3x+y}&{=}&{-1} & {2x +y}&{=}&{0}\\{3(-1)+ 2}&{\stackrel{?}{=}}&{-1} &{2(-1)+2}&{\stackrel{?}{=}}&{0} \\ {-1}&{=}&{-1 \checkmark}&{0}&{=}&{0 \checkmark} \end{array}\) La solución es (−1, 2).
Resuelve cada sistema graficando:\(\begin{cases}{−x+y=1} \\ {2x+y=10}\end{cases}\)
- Contestar
-
(3,4)
Resuelve cada sistema graficando:\(\begin{cases}{ 2x+y=6} \\ {x+y=1}\end{cases}\)
- Contestar
-
(5, −4)
Por lo general, cuando las ecuaciones se dan en forma estándar, la forma más conveniente de graficarlas es mediante el uso de las intercepciones. Esto lo haremos en Ejercicio\(\PageIndex{13}\).
Resuelve el sistema graficando:\(\begin{cases}{x+y=2} \\ {x−y=4}\end{cases}\)
- Contestar
-
Encontraremos las intercepciones x e y de ambas ecuaciones y las usaremos para graficar las líneas.
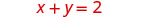
Para encontrar las intercepciones, deja x = 0 y resuelve
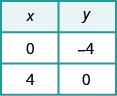
para y, luego deja y = 0 y resuelve para x.\(\begin{aligned} x+y &=2 \quad x+y=2 \\ 0+y &=2 \quad x+0=2 \\ y &=2 \quad x=2 \end{aligned}\) 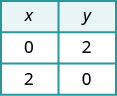
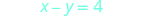
Para encontrar las intercepciones, vamos
x = 0 y luego dejar y = 0.\ begin {array} {rlr} {x-y} & {=4} & {x-y} & {= 4}\\ {0-y} & {=4} & {x-0} & {=4}\\ {-y} & {=4} & {x} & {=4}\\ {y} & {=-4}\ end {array}
Grafica la línea. 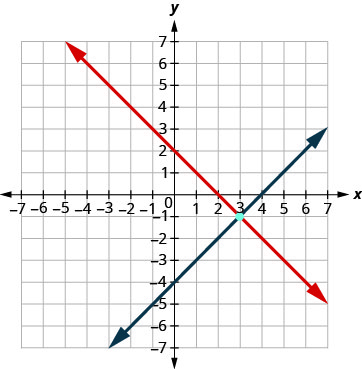
Determinar el punto de intersección. Las líneas se cruzan en (3, −1). Verifique la solución en ambas ecuaciones. \(\begin{array}{rllrll}{x+y}&{=}&{2} & {x-y}&{=}&{4}\\{3+(-1)}&{\stackrel{?}{=}}&{2} &{3 - (-1)}&{\stackrel{?}{=}}&{4} \\ {2}&{=}&{2 \checkmark}&{4}&{=}&{4 \checkmark} \end{array}\)
La solución es (3, −1).
Resuelve cada sistema graficando:\(\begin{cases}{x+y=6} \\ {x−y=2}\end{cases}\)
- Contestar
-
(4,2)
Resuelve cada sistema graficando:\(\begin{cases}{x+y=2} \\ {x−y=-8}\end{cases}\)
- Contestar
-
(5, −3)
¿Recuerdas cómo graficar una ecuación lineal con una sola variable? Será ya sea una línea vertical o una horizontal.
Resuelve el sistema graficando:\(\begin{cases}{y=6} \\ {2x+3y=12}\end{cases}\)
- Contestar
-

Sabemos que la primera ecuación representa una
línea horizontal cuya intersección y es 6.
La segunda ecuación se grafica más convenientemente
usando intercepciones.
Para encontrar las intercepciones, vamos x = 0 y luego y = 0. 
Grafica las líneas. 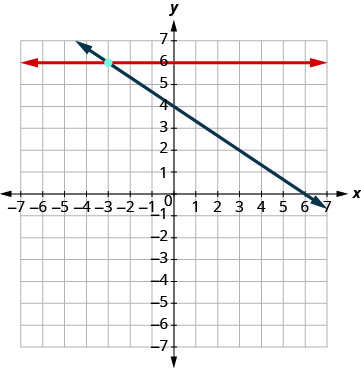
Determinar el punto de intersección. Las líneas se cruzan en (−3, 6). Verifique la solución a ambas ecuaciones. \(\begin{array}{rllrll}{y}&{=}&{6} & {2x+3y}&{=}&{12}\\{6}&{\stackrel{?}{=}}&{6} &{2(-3) + 3(6)}&{\stackrel{?}{=}}&{12} \\ {6}&{=}&{6 \checkmark} &{-6+18}&{\stackrel{?}{=}}&{12} \\ {}&{}&{}&{12}&{=}&{12 \checkmark} \end{array}\) La solución es (−3, 6).
Resuelve cada sistema graficando:\(\begin{cases}{y=−1} \\ {x+3y=6}\end{cases}\)
- Contestar
-
(9, −1)
Resuelve cada sistema graficando:\(\begin{cases}{x=4} \\ {3x−2y=24}\end{cases}\)
- Contestar
-
(4, −6)
En todos los sistemas de ecuaciones lineales hasta el momento, las líneas se cruzaron y la solución fue un punto. En los siguientes dos ejemplos, veremos un sistema de ecuaciones que no tiene solución y un sistema de ecuaciones que tiene un número infinito de soluciones.
Resuelve el sistema graficando:\(\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\)
- Contestar
-
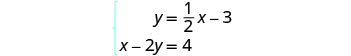
Para graficar la primera ecuación,
utilizaremos su pendiente y -intercepción.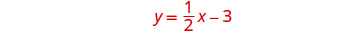
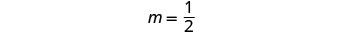
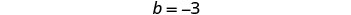
Para graficar la segunda ecuación,
usaremos las intercepciones.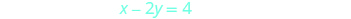
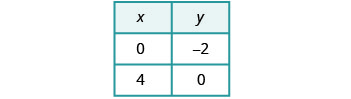
Grafica las líneas. 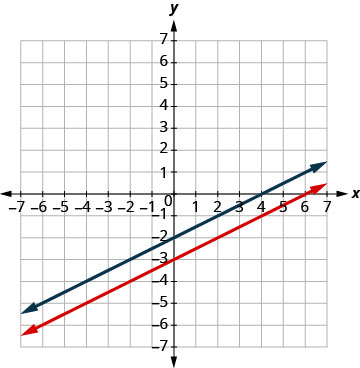
Determinar el punto de intersección. Las líneas son paralelas. Como no hay punto en ambas líneas, no hay par ordenado
que haga que ambas ecuaciones sean verdaderas. No hay solución a
este sistema.
Resuelve cada sistema graficando:\(\begin{cases}{y=-\frac{1}{4}x+2} \\ {x+4y=-8}\end{cases}\)
- Contestar
-
sin solución
Resuelve cada sistema graficando:\(\begin{cases}{y=3x−1} \\ {6x−2y=6}\end{cases}\)
- Contestar
-
sin solución
Resuelve el sistema graficando:\(\begin{cases}{y=2x−3} \\ {−6x+3y=−9}\end{cases}\)
- Contestar
-
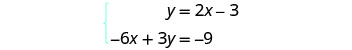
Encuentra la pendiente y -intercepción de la
primera ecuación.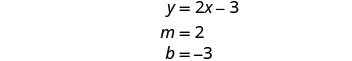
Encuentra las intercepciones de la segunda ecuación. 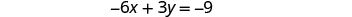
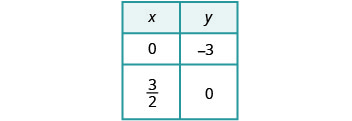
Grafica las líneas. 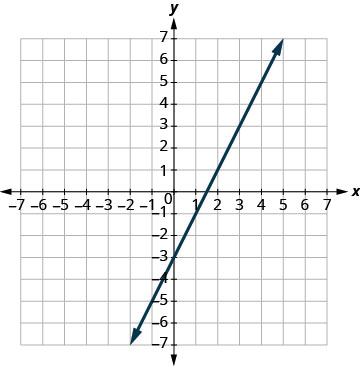
Determinar el punto de intersección. ¡Las líneas son las mismas! Dado que cada punto de la línea hace que ambas ecuaciones sean
verdaderas, hay infinitamente muchos pares ordenados que hacen que
ambas ecuaciones sean verdaderas.Hay infinitamente muchas soluciones a este sistema.
Resuelve cada sistema graficando:\(\begin{cases}{y=−3x−6} \\ {6x+2y=−12}\end{cases}\)
- Contestar
-
infinitamente muchas soluciones
Resuelve cada sistema graficando:\(\begin{cases}{y=\frac{1}{2}x−4} \\ {2x−4y=16}\end{cases}\)
- Contestar
-
infinitamente muchas soluciones
Si escribes la segunda ecuación en Ejercicio\(\PageIndex{22}\) en forma de pendiente-intersección, puedes reconocer que las ecuaciones tienen la misma pendiente y la misma intersección y.
Cuando graficamos la segunda línea en el último ejemplo, la dibujamos justo sobre la primera línea. Decimos que las dos líneas son coincidentes. Las líneas coincidentes tienen la misma pendiente y la misma intersección y.
Las líneas coincidentes tienen la misma pendiente y la misma intersección y.
Determinar el número de soluciones de un sistema lineal
Habrá momentos en los que vamos a querer saber cuántas soluciones habrá para un sistema de ecuaciones lineales, pero en realidad tal vez no tengamos que encontrar la solución. Será útil determinar esto sin graficar.
Hemos visto que dos líneas en un mismo plano deben cruzarse o ser paralelas. Los sistemas de ecuaciones del Ejercicio\(\PageIndex{4}\)\(\PageIndex{16}\) a través del Ejercicio tuvieron dos líneas de intersección. Cada sistema tenía una solución.
Un sistema con líneas paralelas, como Ejercicio\(\PageIndex{19}\), no tiene solución. ¿Qué pasó en Ejercicio\(\PageIndex{22}\)? Las ecuaciones tienen líneas coincidentes, por lo que el sistema tenía infinitamente muchas soluciones.
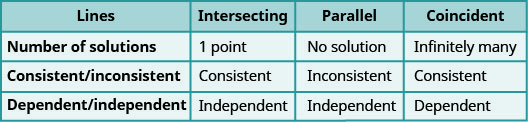
Organizaremos estos resultados en la Figura\(\PageIndex{2}\) a continuación:
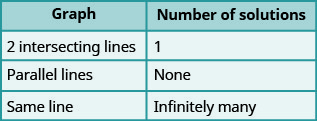
Las líneas paralelas tienen la misma pendiente pero diferentes intersecciones y. Entonces, si escribimos ambas ecuaciones en un sistema de ecuaciones lineales en forma de pendiente-intercepción, ¡podemos ver cuántas soluciones habrá sin graficar! Mira el sistema que resolvimos en Ejercicio\(\PageIndex{19}\).
\(\begin{array} {cc} & \begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\\ \text{The first line is in slope–intercept form.} &\text { If we solve the second equation for } y, \text { we get } \\ &x-2 y =4 \\ y = \frac{1}{2}x -3& x-2 y =-x+4 \\ &y =\frac{1}{2} x-2 \\ m=\frac{1}{2}, b=-3&m=\frac{1}{2}, b=-2 \end{array}\)
Las dos líneas tienen la misma pendiente pero diferentes intersecciones y. Son líneas paralelas.
La figura\(\PageIndex{3}\) muestra cómo determinar el número de soluciones de un sistema lineal observando las pendientes e intercepciones.
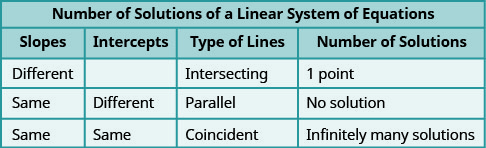
Echemos un vistazo más a nuestras ecuaciones en Ejercicio\(\PageIndex{19}\) que nos dieron líneas paralelas.
\ [\ begin {casos} {y=\ frac {1} {2} x−3}\\ {x−2y=4}\ end {casos}\)]
Cuando ambas líneas estaban en forma de pendiente-intersección teníamos:
\[y=\frac{1}{2} x-3 \quad y=\frac{1}{2} x-2\]
¿Reconoces que es imposible tener un solo par ordenado (x, y) que sea una solución a ambas ecuaciones?
Llamamos a un sistema de ecuaciones como este un sistema inconsistente. No tiene solución.
Un sistema de ecuaciones que tiene al menos una solución se denomina sistema consistente.
Un sistema consistente de ecuaciones es un sistema de ecuaciones con al menos una solución.
Un sistema inconsistente de ecuaciones es un sistema de ecuaciones sin solución.
También categorizamos las ecuaciones en un sistema de ecuaciones llamando a las ecuaciones independientes o dependientes. Si dos ecuaciones son ecuaciones independientes, cada una de ellas tiene su propio conjunto de soluciones. Las líneas que se cruzan y las líneas paralelas son independientes.
Si dos ecuaciones son dependientes, todas las soluciones de una ecuación también son soluciones de la otra ecuación. Cuando graficamos dos ecuaciones dependientes, obtenemos líneas coincidentes.
Dos ecuaciones son independientes si tienen diferentes soluciones.
Dos ecuaciones son dependientes si todas las soluciones de una ecuación son también soluciones de la otra ecuación.
Resumamos esto mirando las gráficas de los tres tipos de sistemas. Ver Figura\(\PageIndex{4}\) y Figura\(\PageIndex{5}\).
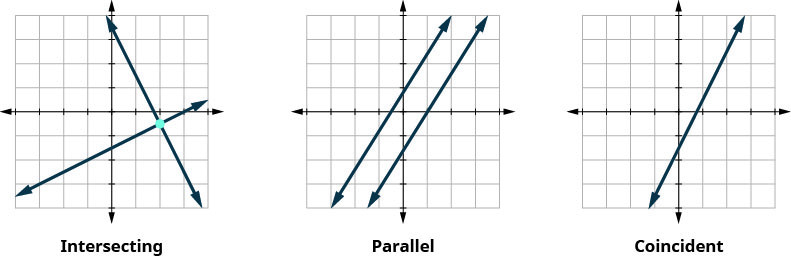
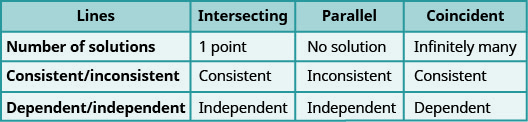
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones:\(\begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases}\)
- Contestar
-
\(\begin{array}{lrrl} \text{We will compare the slopes and intercepts} & \begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases} \\ \text{of the two lines.} \\ \text{The first equation is already in} \\ \text{slope-intercept form.} \\ & {y = 3x - 1}\\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ & 6x-2y &=&12 \\ & -2y &=& -6x - 12 \\ &\frac{-2y}{-2} &=& \frac{-6x + 12}{-2}\\ &y&=&3x-6\\\\ \text{Find the slope and intercept of each line.} & y = 3x-1 & y=3x-6 \\ &m = 3 & m = 3 \\&b=-1 &b=-6 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)
Un sistema de ecuaciones cuyas gráficas son líneas paralelas no tiene solución y es inconsistente e independiente.
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\begin{cases}{y=−2x−4} \\ {4x+2y=9}\end{cases}\)
- Contestar
-
sin solución, inconsistente, independiente
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\begin{cases}{y=\frac{1}{3}x−5} \\ {x-3y=6}\end{cases}\)
- Contestar
-
sin solución, inconsistente, independiente
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones:\(\begin{cases}{2x+y=−3} \\ {x−5y=5}\end{cases}\)
- Contestar
-
\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts} & \begin{cases}{2x+y=-3} \\ {x−5y=5}\end{cases} \\ \text{of the two lines.} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &2x+y&=&-3 & x−5y&=&5\\ & y &=& -2x -3 & -5y &=&-x+5 \\ &&&&\frac{-5y}{-5} &=& \frac{-x + 5}{-5}\\ &&&&y&=&\frac{1}{5}x-1\\\\ \text{Find the slope and intercept of each line.} & y &=& -2x-3 & y&=&\frac{1}{5}x-1 \\ &m &=& -2 & m &=& \frac{1}{5} \\&b&=&-3 &b&=&-1 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)
Un sistema de ecuaciones cuyas gráficas se cruzan tiene 1 solución y es consistente e independiente.
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\begin{cases}{3x+2y=2} \\ {2x+y=1}\end{cases}\)
- Contestar
-
una solución, consistente, independiente
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\begin{cases}{x+4y=12} \\ {−x+y=3}\end{cases}\)
- Contestar
-
una solución, consistente, independiente
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones. \(\begin{cases}{3x−2y=4} \\ {y=\frac{3}{2}x−2}\end{cases}\)
- Contestar
-
\(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts of the two lines.}& \begin{cases}{3x−2y} &=&{4} \\ {y}&=&{\frac{3}{2}x−2}\end{cases} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &3x-2y&=&4 \\ & -2y &=& -3x +4 \\ &\frac{-2y}{-2} &=& \frac{-3x + 4}{-2}\\ &y&=&\frac{3}{2}x-2\\\\ \text{Find the slope and intercept of each line.} &y&=&\frac{3}{2}x-2\\ \text{Since the equations are the same, they have the same slope} \\ \text{and samey-intercept and so the lines are coincident.}\end{array}\)
Un sistema de ecuaciones cuyas gráficas son líneas coincidentes tiene infinitamente muchas soluciones y es consistente y dependiente.
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\begin{cases}{4x−5y=20} \\ {y=\frac{4}{5}x−4}\end{cases}\)
- Contestar
-
infinitamente muchas soluciones, consistentes, dependientes
Sin graficar, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\begin{cases}{ −2x−4y=8} \\ {y=−\frac{1}{2}x−2}\end{cases}\)
- Contestar
-
infinitamente muchas soluciones, consistentes, dependientes
Resolver aplicaciones de sistemas de ecuaciones mediante gráficos
Utilizaremos la misma estrategia de resolución de problemas que usamos en Modelos Matemáticos para configurar y resolver aplicaciones de sistemas de ecuaciones lineales. Modificaremos la estrategia ligeramente aquí para que sea apropiada para sistemas de ecuaciones.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija variables para representar esas cantidades.
- Traducir en un sistema de ecuaciones.
- Resolver el sistema de ecuaciones utilizando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
El paso 5 es donde utilizaremos el método introducido en esta sección. Graficaremos las ecuaciones y encontraremos la solución.
Sondra está haciendo 10 cuartos de ponche de jugo de frutas y refrescos de club. El número de cuartos de jugo de frutas es 4 veces el número de cuartos de galón de soda club. ¿Cuántos cuartos de jugo de frutas y cuántos cuartos de refresco club necesita Sondra?
- Contestar
-
Paso 1. Lee el problema.
Paso 2. Identificar lo que estamos buscando.
Estamos buscando la cantidad de cuartos de jugo de frutas y el número de cuartos de galón de refresco club que Sondra necesitará.
Paso 3. Nombra lo que estamos buscando. Elija variables para representar esas cantidades.
Dejar f= número de cuartos de galón de jugo de fruta.
c= número de cuartos de galón de soda clubPaso 4. Traducir en un sistema de ecuaciones.
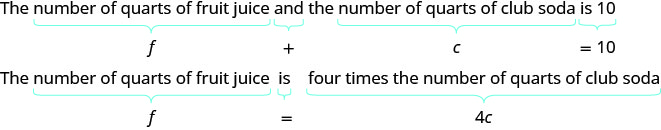
Ahora tenemos el sistema. \(\begin{cases}{ f+c=10} \\ {f=4c}\end{cases}\)
Paso 5. Resolver el sistema de ecuaciones utilizando buenas técnicas de álgebra.
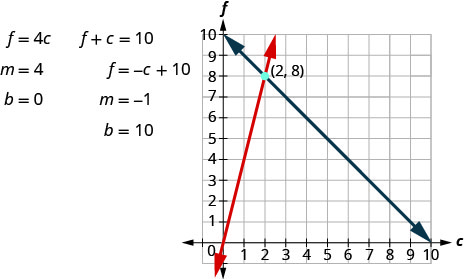
El punto de intersección (2, 8) es la solución. Esto significa que Sondra necesita 2 cuartos de refresco club y 8 cuartos de jugo de frutas.
Paso 6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
¿Esto tiene sentido en el problema?
Sí, el número de cuartos de jugo de frutas, 8 es 4 veces el número de cuartos de galón de soda club, 2.
Sí, 10 cuartos de ponche son 8 cuartos de jugo de fruta más 2 cuartos de galón de soda club.
Paso 7. Contesta la pregunta con una oración completa.
Sondra necesita 8 cuartos de jugo de frutas y 2 cuartos de refresco.
Manny está haciendo 12 cuartos de jugo de naranja con concentrado y agua. El número de cuartos de galón de agua es 3 veces el número de cuartos de concentrado. ¿Cuántos cuartos de concentrado y cuántos cuartos de agua necesita Manny?
- Contestar
-
Manny necesita concentrado de jugo de 3 cuartos y 9 cuartos de agua.
Alisha está haciendo una bebida de café de 18 onzas que está hecha de café y leche elaborados. El número de onzas de café elaborado es 5 veces mayor que el número de onzas de leche. ¿Cuántas onzas de café y cuántas onzas de leche necesita Alisha?
- Contestar
-
Alisha necesita 15 onzas de café y 3 onzas de leche.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con sistemas de resolución de ecuaciones mediante gráficos.
Conceptos clave
- Resolver un sistema de ecuaciones lineales mediante la gráfica
- Grafica la primera ecuación.
- Grafique la segunda ecuación en el mismo sistema de coordenadas rectangulares.
- Determine si las líneas se cruzan, son paralelas o son la misma línea.
- Identificar la solución al sistema.
Si las líneas se cruzan, identifique el punto de intersección. Verifique para asegurarse de que sea una solución a ambas ecuaciones. Esta es la solución al sistema.
Si las líneas son paralelas, el sistema no tiene solución.
Si las líneas son las mismas, el sistema tiene un número infinito de soluciones. - Verifique la solución en ambas ecuaciones.
- Determinar el número de soluciones a partir de la gráfica de un sistema lineal
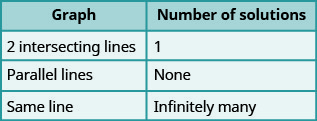
- Determinar el número de soluciones de un sistema lineal observando las pendientes e intercepciones
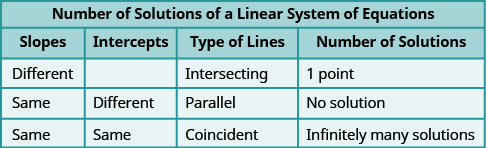
- Determinar el número de soluciones y cómo clasificar un sistema de ecuaciones
- Estrategia de Resolución de Problemas para Sistemas de Ecuaciones Lineales
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija variables para representar esas cantidades.
- Traducir en un sistema de ecuaciones.
- Resolver el sistema de ecuaciones utilizando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
Glosario
- líneas coincidentes
- Las líneas coincidentes son líneas que tienen la misma pendiente y la misma intersección y.
- sistema consistente
- Un sistema consistente de ecuaciones es un sistema de ecuaciones con al menos una solución.
- ecuaciones dependientes
- Dos ecuaciones son dependientes si todas las soluciones de una ecuación son también soluciones de la otra ecuación.
- sistema inconsistente
- Un sistema inconsistente de ecuaciones es un sistema de ecuaciones sin solución.
- ecuaciones independientes
- Dos ecuaciones son independientes si tienen diferentes soluciones.
- soluciones de un sistema de ecuaciones
- Las soluciones de un sistema de ecuaciones son los valores de las variables que hacen verdaderas todas las ecuaciones. Una solución de un sistema de dos ecuaciones lineales está representada por un par ordenado (x, y).
- sistema de ecuaciones lineales
- Cuando se agrupan dos o más ecuaciones lineales, forman un sistema de ecuaciones lineales.


