5.1E: Ejercicios
- Page ID
- 110178
La práctica hace la perfección
Determinar si un Par Ordenado es una Solución de un Sistema de Ecuaciones. En los siguientes ejercicios, determinar si los siguientes puntos son soluciones al sistema de ecuaciones dado.
\(\begin{cases}{2x−6y=0} \\ {3x−4y=5}\end{cases}\)
- (3,1)
- (−3,4)
- Contestar
-
- si
- no
\(\begin{cases}{7x-4y=-1} \\ {-3x-2y = 1} \end{cases}\)
- (\(-\frac{3}{13}\),\(-\frac{2}{13}\))
- (1, -2)
- Contestar
-
- si
- no
\(\left\{\begin{array}{l}{2 x+y=5} \\ {x+y=1}\end{array}\right.\)
- (4, −3)
- (2,0)
- Contestar
-
- si
- no
\(\left\{\begin{array}{l}{-3 x+y=8} \\ {-x+2 y=-9}\end{array}\right.\)
- (−5, −7)
- (−5,7)
\(\left\{\begin{array}{l}{x+y=2} \\ {y=\frac{3}{4} x}\end{array}\right.\)
- \(\left(\frac{8}{7}, \frac{6}{7}\right)\)
- \(\left(1, \frac{3}{4}\right)\)
- Contestar
-
- si
- no
\(\left\{\begin{array}{l}{x+y=1} \\ {y=\frac{2}{5} x}\end{array}\right.\)
- \(\left(\frac{5}{7}, \frac{2}{7}\right)\)
- (5,2)
\(\left\{\begin{array}{l}{x+5 y=10} \\ {y=\frac{3}{5} x+1}\end{array}\right.\)
- (−10,4)
- \(\left(\frac{5}{4}, \frac{7}{4}\right)\)
- Contestar
-
- no
- si
\(\left\{\begin{array}{l}{x+3 y=9} \\ {y=\frac{2}{3} x-2}\end{array}\right.\)
- (−6,5)
- \(\left(5, \frac{4}{3}\right)\)
Resolver un Sistema de Ecuaciones Lineales Gráficando En los siguientes ejercicios, resuelve los siguientes sistemas de ecuaciones graficando.
\(\left\{\begin{array}{l}{3 x+y=-3} \\ {2 x+3 y=5}\end{array}\right.\)
- Contestar
-
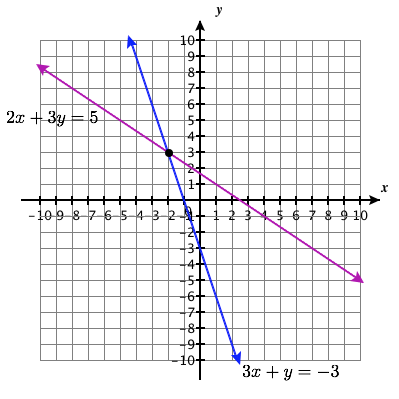
Punto de solución:\((-2,3)\)
\(\left\{\begin{array}{l}{-x+y=2} \\ {2 x+y=-4}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+y=-1} \\ {2 x+y=4}\end{array}\right.\)
- Contestar
-
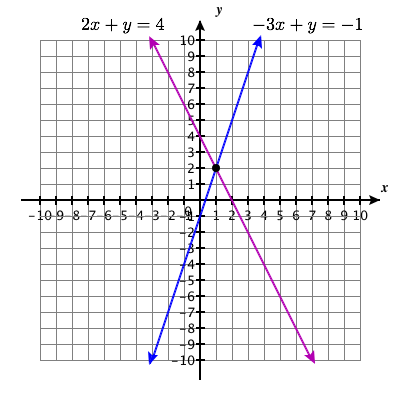
Punto de solución:\((1,2)\)
\(\left\{\begin{array}{l}{-2 x+3 y=-3} \\ {x+y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=x+2} \\ {y=-2 x+2}\end{array}\right.\)
- Contestar
-
Punto de solución:\((0,2)\)
\(\left\{\begin{array}{l}{y=x-2} \\ {y=-3 x+2}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=\frac{3}{2} x+1} \\ {y=-\frac{1}{2} x+5}\end{array}\right.\)
- Contestar
-
Punto de solución:\((2,4)\)
\(\left\{\begin{array}{l}{y=\frac{2}{3} x-2} \\ {y=-\frac{1}{3} x-5}\end{array}\right.\)
\(\left\{\begin{array}{l}{-x+y=-3} \\ {4 x+4 y=4}\end{array}\right.\)
- Contestar
-
Punto de solución:\((2,-1)\)
\(\left\{\begin{array}{l}{x-y=3} \\ {2 x-y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+y=-1} \\ {2 x+y=4}\end{array}\right.\)
- Contestar
-
Punto de solución:\((1,2)\)
\(\left\{\begin{array}{l}{-3 x+y=-2} \\ {4 x-2 y=6}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=5} \\ {2 x-y=4}\end{array}\right.\)
- Contestar
-
Punto de solución:\((3,2)\)
\(\left\{\begin{array}{l}{x-y=2} \\ {2 x-y=6}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=2} \\ {x-y=0}\end{array}\right.\)
- Contestar
-
Punto de solución:\((1,1)\)
\(\left\{\begin{array}{l}{x+y=6} \\ {x-y=-8}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=-5} \\ {x-y=3}\end{array}\right.\)
- Contestar
-
Punto de solución:\((-1,-4)\)
\(\left\{\begin{array}{l}{x+y=4} \\ {x-y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=-4} \\ {-x+2 y=-2}\end{array}\right.\)
- Contestar
-
Punto de solución:\((3,3)\)
\(\left\{\begin{array}{l}{-x+3 y=3} \\ {x+3 y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{-2 x+3 y=3} \\ {x+3 y=12}\end{array}\right.\)
- Contestar
-
Punto de solución:\((-5,6)\)
\(\left\{\begin{array}{l}{2 x-y=4} \\ {2 x+3 y=12}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x+3 y=6} \\ {y=-2}\end{array}\right.\)
- Contestar
-
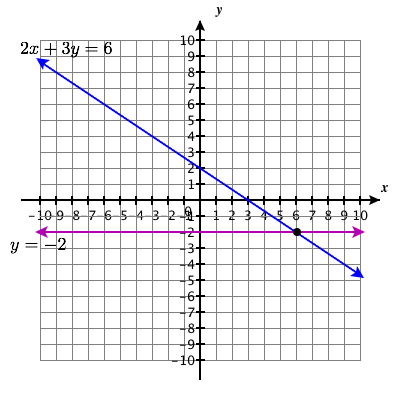
Punto de solución:\((6,−2)\)
\(\left\{\begin{array}{l}{-2 x+y=2} \\ {y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-3 y=-3} \\ {y=2}\end{array}\right.\)
Contestar
-
Punto de solución:\((3,2)\)
\(\left\{\begin{array}{l}{2 x-2 y=8} \\ {y=-3}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-y=-1} \\ {x=1}\end{array}\right.\)
- Contestar
-
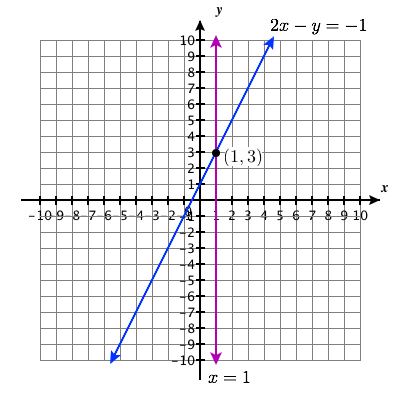
Punto de solución:\((1,3)\)
\(\left\{\begin{array}{l}{x+2 y=2} \\ {x=-2}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-3 y=-6} \\ {x=-3}\end{array}\right.\)
- Contestar
-
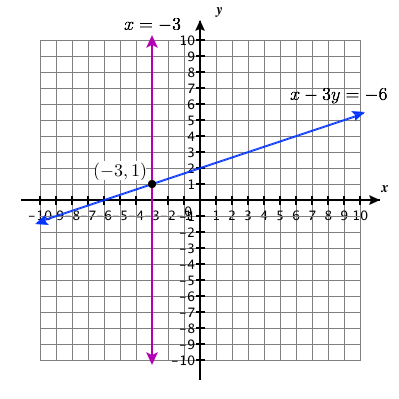
Punto de solución:\((−3,1)\)
\(\left\{\begin{array}{l}{x+y=4} \\ {x=1}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x-3 y=8} \\ {8 x-6 y=14}\end{array}\right.\)
- Contestar
-
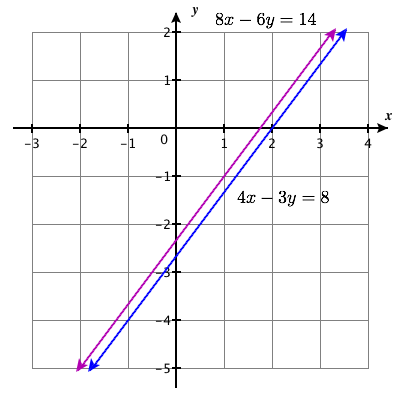
sin solución
\(\left\{\begin{array}{l}{x+3 y=4} \\ {-2 x-6 y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{-2 x+4 y=4} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- Contestar
-
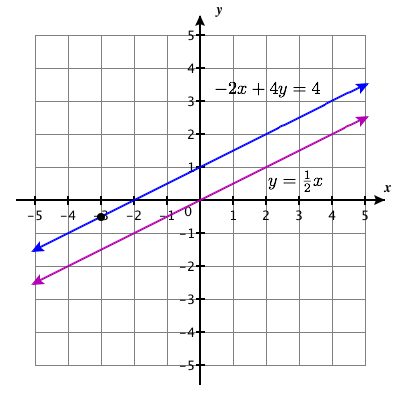
sin solución
\(\left\{\begin{array}{l}{3 x+5 y=10} \\ {y=-\frac{3}{5} x+1}\end{array}\right.\)
\(\left\{\begin{array}{l}{x=-3 y+4} \\ {2 x+6 y=8}\end{array}\right.\)
- Contestar
-
no hay solución
\(\left\{\begin{array}{l}{4 x=3 y+7} \\ {8 x-6 y=14}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x+y=6} \\ {-8 x-4 y=-24}\end{array}\right.\)
- Contestar
-
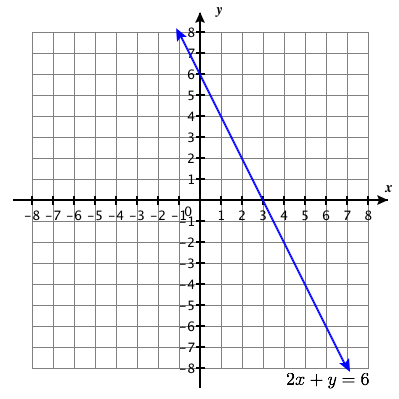
infinitamente muchas soluciones con conjunto de soluciones:\(\big\{ (x,y) | 2 x+y=6\big\}\)
\(\left\{\begin{array}{l}{5 x+2 y=7} \\ {-10 x-4 y=-14}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+3 y=-6} \\ {4 y=-\frac{4}{3} x-8}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones con conjunto de soluciones:\(\big\{ (x,y) | x+3 y=-6\big\}\)
\(\left\{\begin{array}{l}{-x+2 y=-6} \\ {y=-\frac{1}{2} x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+2 y=-2} \\ {y=-x+4}\end{array}\right.\)
- Contestar
-
Punto de solución:\((2,2)\)
\(\left\{\begin{array}{l}{-x+2 y=-2} \\ {y=-x-1}\end{array}\right.\)
Determinar el número de soluciones de un sistema lineal Sin graficar los siguientes sistemas de ecuaciones, determinar el número de soluciones y luego clasificar el sistema de ecuaciones.
\(\left\{\begin{array}{l}{y=\frac{2}{3} x+1} \\ {-2 x+3 y=5}\end{array}\right.\)
- Contestar
-
0 soluciones
\(\left\{\begin{array}{l}{y=\frac{1}{3} x+2} \\ {x-3 y=9}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-2 x+1} \\ {4 x+2 y=8}\end{array}\right.\)
- Contestar
-
0 soluciones
\(\left\{\begin{array}{l}{y=3 x+4} \\ {9 x-3 y=18}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=\frac{2}{3} x+1} \\ {2 x-3 y=7}\end{array}\right.\)
- Contestar
-
0 soluciones
\(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=-3 x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x+2 y=10} \\ {4 x-2 y=-6}\end{array}\right.\)
- Contestar
-
consistente, 1 solución
\(\left\{\begin{array}{l}{5 x+3 y=4} \\ {2 x-3 y=5}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-\frac{1}{2} x+5} \\ {x+2 y=10}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
\(\left\{\begin{array}{l}{y=x+1} \\ {-x+y=1}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=2 x+3} \\ {2 x-y=-3}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
\(\left\{\begin{array}{l}{5 x-2 y=10} \\ {y=\frac{5}{2} x-5}\end{array}\right.\)
Resolver Aplicaciones de Sistemas de Ecuaciones Graficando En los siguientes ejercicios, resuelve.
Molly está haciendo agua con infusión de fresa. Por cada onza de jugo de fresa, usa tres veces más onzas de agua. ¿Cuántas onzas de jugo de fresa y cuántas onzas de agua necesita para hacer 64 onzas de agua con infusión de fresa?
- Contestar
-
Molly necesita 16 onzas de jugo de fresa y 48 onzas de agua.
Jamal está haciendo una mezcla de refrigerios que contiene solo pretzels y nueces. Por cada onza de nueces, usará 2 onzas de pretzels. ¿Cuántas onzas de pretzels y cuántas onzas de nueces necesita para hacer 45 onzas de mezcla para refrigerios?
Enrique está haciendo una mezcla de fiesta que contiene pasas y nueces. Por cada onza de frutos secos, usa el doble de la cantidad de pasas. ¿Cuántas onzas de nueces y cuántas onzas de pasas necesita para hacer 24 onzas de mezcla de fiesta?
- Contestar
-
Enrique necesita 8 onzas de nueces y 16 onzas de agua.
Owen está haciendo limonada a partir de concentrado. El número de cuartos de galón de agua que necesita es 4 veces el número de cuartos de concentrado. ¿Cuántos cuartos de agua y cuántos cuartos de concentrado necesita Owen para hacer 100 cuartos de limonada?
Matemáticas cotidianas
Leo está planeando su jardín de flores de primavera. Quiere plantar bulbos de tulipán y narciso. Plantará 6 veces más bulbos de narciso que bulbos de tulipán. Si quiere plantar 350 bulbos, ¿cuántos bulbos de tulipán y cuántos bulbos de narciso debería plantar?
- Contestar
-
Leo debe plantar 50 tulipanes y 300 narcisos.
Una empresa de marketing encuesta a 1,200 personas. Encuestaron el doble de mujeres que de machos. ¿Cuántos hombres y mujeres encuestaron?
Ejercicios de escritura
En un sistema de ecuaciones lineales, las dos ecuaciones tienen la misma pendiente. Describir las posibles soluciones al sistema.
- Contestar
-
Dado que sólo se sabe que las pendientes de ambas ecuaciones lineales son las mismas, o no hay soluciones (las gráficas de las ecuaciones son paralelas) o infinitamente muchas.
En un sistema de ecuaciones lineales, las dos ecuaciones tienen las mismas intercepciones. Describir las posibles soluciones al sistema.
Autocomprobación
Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
Si la mayoría de tus cheques fueron:
... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.
... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no - ¡No lo consigo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.


