5.2: Resolver Sistemas de Ecuaciones por Sustitución
- Page ID
- 110155
Al final de esta sección, podrás:
- Resolver un sistema de ecuaciones por sustitución
- Resolver aplicaciones de sistemas de ecuaciones por sustitución
Antes de comenzar, toma este cuestionario de preparación.
- Simplifique −5 (3−x).
Si te perdiste este problema, revisa Ejercicio 1.10.43. - Simplifique 4−2 (n+5).
Si te perdiste este problema, revisa Ejercicio 1.10.41. - Resuelve para y. 8y−8=32−2y
Si te perdiste este problema, revisa Ejercicio 2.3.22. - Resuelve para x. 3x−9y=−3
Si te perdiste este problema, revisa Ejercicio 2.6.22.
Resolver sistemas de ecuaciones lineales mediante gráficos es una buena manera de visualizar los tipos de soluciones que pueden resultar. Sin embargo, hay muchos casos en los que resolver un sistema mediante la gráfica es inconveniente o impreciso. Si los gráficos se extienden más allá de la cuadrícula pequeña con x e y ambos entre −10 y 10, graficar las líneas puede ser engorroso. Y si las soluciones al sistema no son números enteros, puede ser difícil leer sus valores precisamente a partir de una gráfica.
En esta sección, resolveremos sistemas de ecuaciones lineales por el método de sustitución.
Resolver un Sistema de Ecuaciones por Sustitución
Utilizaremos el mismo sistema que usamos primero para graficar.
\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
Primero resolveremos una de las ecuaciones para x o y. Podemos elegir cualquiera de las ecuaciones y resolver para cualquiera de las variables, pero intentaremos tomar una decisión que mantenga el trabajo fácil.
Entonces sustituimos esa expresión por la otra ecuación. El resultado es una ecuación con una sola variable, ¡y sabemos cómo resolverlas!
Después de encontrar el valor de una variable, sustituiremos ese valor en una de las ecuaciones originales y resolveremos por la otra variable. Finalmente, comprobamos nuestra solución y nos aseguramos de que haga que ambas ecuaciones sean verdaderas.
Completaremos todos estos pasos ahora en Ejercicio\(\PageIndex{1}\).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- Contestar
-






Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)
- Contestar
-
(6,1)
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)
- Contestar
-
(4,2)
- Resuelve una de las ecuaciones para cualquiera de las variables.
- Sustituya la expresión del Paso 1 en la otra ecuación.
- Resuelve la ecuación resultante.
- Sustituya la solución del Paso 3 por una de las ecuaciones originales para encontrar la otra variable.
- Escribe la solución como un par ordenado.
- Comprobar que el par ordenado es una solución a ambas ecuaciones originales.
Si una de las ecuaciones del sistema se da en forma de pendiente-intercepción, ¡el Paso 1 ya está hecho! Veremos esto en Ejercicio\(\PageIndex{4}\).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)
- Contestar
-
La segunda ecuación ya está resuelta para y. Sustituiremos la expresión en lugar de y en la primera ecuación.
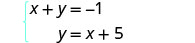
La segunda ecuación ya está resuelta para y.
Vamos a sustituir en la primera ecuación.Reemplace la y por x + 5. 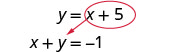
Resuelve la ecuación resultante para x. 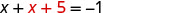
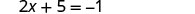
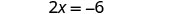
Sustituye x = −3 en y = x + 5 para encontrar y. 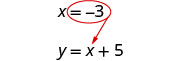
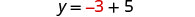
El par ordenado es (−3, 2). 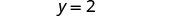
Verifique el par ordenado en ambas ecuaciones:
\(\begin{array} {rllrll} x+y &=&-1 & y&=&x+5\\-3+2 &\stackrel{?}{=}&-1 &2& \stackrel{?}{=} & -3 + 5\\-1 &=&-1\checkmark &2 &=&2\checkmark \end{array}\)La solución es (−3, 2).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)
- Contestar
-
(2,4)
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)
- Contestar
-
(−1, −3)
Si las ecuaciones se dan en forma estándar, tendremos que comenzar resolviendo para una de las variables. En este siguiente ejemplo, resolveremos la primera ecuación para y.
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)
- Contestar
-
Necesitamos resolver una ecuación para una variable. Entonces sustituiremos esa expresión por la otra ecuación.
Resolver por y.
Sustituir en la otra ecuación.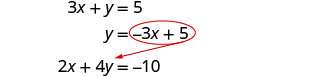
Sustituya la y por −3 x + 5. 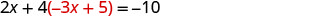
Resuelve la ecuación resultante para x. 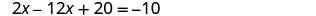
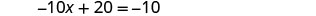
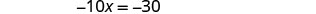
Sustituye x = 3 en 3 x + y = 5 para encontrar y. 


El par ordenado es (3, −4). 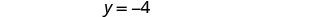
Verifique el par ordenado en ambas ecuaciones:
\(\begin{array} {rllrll} 3x+y &=&5 & 2x+4y&=&-10\\3\cdot3+(-4) &\stackrel{?}{=}&5 &2\cdot3 + 4(-4)& \stackrel{?}{=} & -10\\9-4&\stackrel{?}{=}&5 &6-16& \stackrel{?}{=} & -10\\5 &=&5\checkmark &-10&=&-10\checkmark \end{array}\)La solución es (3, −4).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)
- Contestar
-
(1, −2)
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)
- Contestar
-
(2,6)
En Ejercicio\(\PageIndex{7}\) fue más fácil resolver para y en la primera ecuación porque tenía un coeficiente de 1. En Ejercicio\(\PageIndex{10}\) será más fácil resolver para x.
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)
- Contestar
-
Resolveremos la primera ecuación para xx y luego sustituiremos la expresión por la segunda ecuación.

Resolver para x.
Sustituir en la otra ecuación.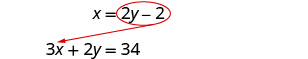
Reemplace la x por 2 y − 2. 
Resolver la ecuación resultante para y. 
Sustituye y = 5 en x − 2 y = −2 para encontrar x.

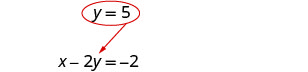



El par ordenado es (8, 5). Verifique el par ordenado en ambas ecuaciones:
\(\begin{array} {rllrll} x-2y &=&-2 & 3x+2y&=&34\\8-2\cdot 5 &\stackrel{?}{=}&-2 &3\cdot8 + 2\cdot5& \stackrel{?}{=} & 34\\8-10&\stackrel{?}{=}&-2 &24+10& \stackrel{?}{=} & 34\\-2 &=&-2\checkmark &34&=&34\checkmark \end{array}\)La solución es (8, 5).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)
- Contestar
-
(−2, −3)
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)
- Contestar
-
(6,2)
Cuando ambas ecuaciones ya están resueltas para la misma variable, ¡es fácil sustituirla!
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- Contestar
-
Dado que ambas ecuaciones se resuelven por y, podemos sustituir una por la otra.
Sustituye\(\frac{1}{2}x\) y en la primera ecuación. 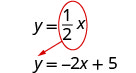
Reemplazar la y con\(\frac{1}{2}x\) 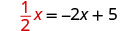
Resuelve la ecuación resultante. Comience
limpiando la fracción.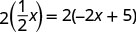
Resolver para x. 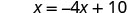
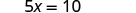
Sustituye x = 2 en\(y = \frac{1}{2}x\) para encontrar y. 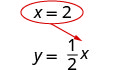
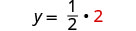
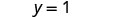
El par ordenado es (2,1). Verifique el par ordenado en ambas ecuaciones:
\(\begin{array} {rllrll} y &=&\frac{1}{2}x & y&=&-2x+5\\1 &\stackrel{?}{=}&\frac{1}{2}\cdot2 &1& \stackrel{?}{=} & -2\cdot2+5\\1 &=&1\checkmark &1 &=&-4+5\\ &&&1&=&1\checkmark \end{array}\)La solución es (2,1).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)
- Contestar
-
(6,2)
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)
- Contestar
-
(8,2)
Ten mucho cuidado con las señales en el siguiente ejemplo.
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)
- Contestar
-
Necesitamos resolver una ecuación para una variable. Vamos a resolver la primera ecuación para y.

Resuelve la primera ecuación para y. 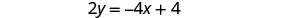
Sustituye −2 x + 2 por y en la segunda ecuación. 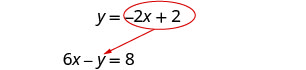
Sustituya la y por −2 x + 2. 
Resuelve la ecuación para x. 


Sustituir\(x = \frac{5}{4}\) en 4 x + 2 y = 4 para encontrar y.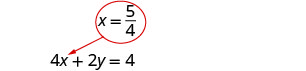



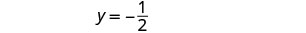
El par ordenado es\((\frac{5}{4},−\frac{1}{2})\). Verifique el par ordenado en ambas ecuaciones.
\(\begin{array} {rllrll} 4x+2y &=&4& 6x-y&=&8\\4(\frac{5}{4}) +2(-\frac{1}{2})&\stackrel{?}{=}&4 &6(\frac{5}{4}) - (-\frac{1}{2})& \stackrel{?}{=} & 8\\5-1&\stackrel{?}{=}&4 &\frac{15}{4} - (-\frac{1}{2}) &\stackrel{?}{=} & 8\\4 &=&4\checkmark &\frac{16}{2} &\stackrel{?}{=}&8\\ &&&8&=&8\checkmark \end{array}\)La solución es (54, −12).
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
- Contestar
-
\((2,\frac{3}{2})\)
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)
- Contestar
-
\((−\frac{1}{2},−2)\)
En Ejemplo, tomará un poco más de trabajo resolver una ecuación para x o y.
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)
- Contestar
-
Necesitamos resolver una ecuación para una variable. Vamos a resolver la primera ecuación para x.
Dado que 0 = 0 es una declaración verdadera, el sistema es consistente. Las ecuaciones son dependientes. Las gráficas de estas dos ecuaciones darían la misma línea. El sistema tiene infinitamente muchas soluciones.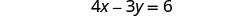
Resuelve la primera ecuación para x. 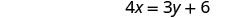
Sustituye\(\frac{3}{4} y+\frac{3}{2}\) x en la segunda ecuación. 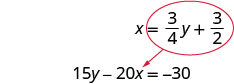
Reemplace la x con\(\frac{3}{4} y+\frac{3}{2}\) 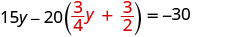
Resolver por y. 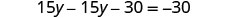
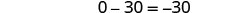

Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
Mirar hacia atrás en las ecuaciones en Ejercicio\(\PageIndex{22}\). ¿Hay alguna manera de reconocer que son la misma línea?
Veamos qué pasa en el siguiente ejemplo.
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)
- Contestar
-
La segunda ecuación ya está resuelta para y, por lo que podemos sustituir a y en la primera ecuación.
Dado que 0 = −10 es una declaración falsa, las ecuaciones son inconsistentes. Las gráficas de las dos ecuaciones serían líneas paralelas. El sistema no tiene soluciones.Sustituir x por y en la primera ecuación. 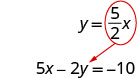
Reemplazar la y con\(\frac{5}{2}x\). 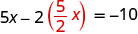
Resolver para x. 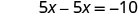

Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)
- Contestar
-
sin solución
Resolver el sistema por sustitución. \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)
- Contestar
-
sin solución
Resolver Aplicaciones de Sistemas de Ecuaciones por Sustitución
Copiaremos aquí la estrategia de resolución de problemas que utilizamos en la sección Resolver sistemas de ecuaciones mediante gráficos para resolver sistemas de ecuaciones. Ahora que sabemos resolver sistemas por sustitución, eso es lo que haremos en el Paso 5.
- Lee el problema. Asegúrese de que se entiendan todas las palabras e ideas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija variables para representar esas cantidades.
- Traducir en un sistema de ecuaciones.
- Resolver el sistema de ecuaciones utilizando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
A algunas personas les resulta más fácil configurar problemas de palabras con dos variables que configurarlos con una sola variable. Elegir los nombres de las variables es más fácil cuando todo lo que necesitas hacer es anotar dos letras. Piensa en esto en el siguiente ejemplo, ¿cómo lo habrías hecho con una sola variable?
La suma de dos números es cero. Un número es nueve menos que el otro. Encuentra los números.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. Estamos buscando dos números. Paso 3. Nombra lo que estamos buscando. Dejar n= el primer número
Let m= el segundo númeroPaso 4. Traducir en un sistema de ecuaciones. La suma de dos números es cero. 
Un número es nueve menos que el otro. 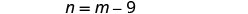
El sistema es: 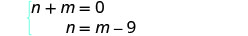
Paso 5. Resolver el sistema de
ecuaciones. Usaremos la sustitución
ya que la segunda ecuación se resuelve
para n.Sustituye m − 9 por n en la primera ecuación. 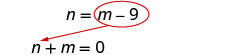
Resolver para m. 


Sustituir\(m=\frac{9}{2}\) en la segunda ecuación
y luego resolver por n.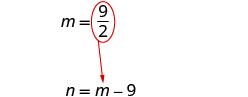
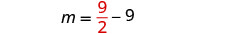
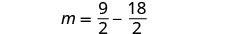
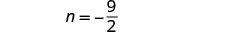
Paso 6. Consulta la respuesta en el problema. ¿Estos números tienen sentido en
el problema? ¡Te lo dejaremos a ti!Paso 7. Contesta la pregunta. Los números son\(\frac{9}{2}\) y\(-\frac{9}{2}\).
La suma de dos números es 10. Un número es 4 menos que el otro. Encuentra los números.
- Contestar
-
Los números son 3 y 7.
La suma de dos números es −6. Un número es 10 menos que el otro. Encuentra los números.
- Contestar
-
Los números son 2 y −8.
En el Ejercicio\(\PageIndex{28}\), usaremos la fórmula para el perímetro de un rectángulo, P = 2 L + 2 W.
Agrega texto de ejercicios aquí.
- Contestar
-
Paso 1. Lee el problema. 
Paso 2. Identifica lo que buscas. Estamos buscando el largo y ancho. Paso 3. Nombra lo que estamos buscando. L= la longitud
W= la anchuraPaso 4. Traducir en un sistema de ecuaciones. El perímetro de un rectángulo es 88. 2 L + 2 W = P
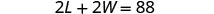
El largo es de cinco más del doble de ancho. 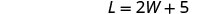
El sistema es: 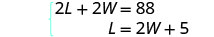
Paso 5. Resolver el sistema de ecuaciones.
Usaremos la sustitución ya que la segunda
ecuación se resuelve para L.
Sustituye 2 W + 5 por L en la primera ecuación.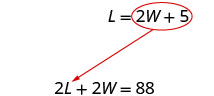
Resolver para W. 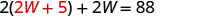
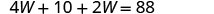
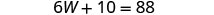
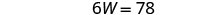
Sustituye W = 13 en la segunda
ecuación y luego resuelve para L.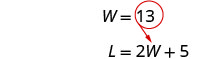
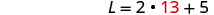
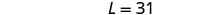
Paso 6. Consulta la respuesta en el problema. ¿Un rectángulo con largo 31 y ancho
13 tiene perímetro 88? Sí.Paso 7. Contesta la ecuación. El largo es 31 y el ancho es 13.
El perímetro de un rectángulo es 40. El largo es 4 más que el ancho. Encuentra el largo y ancho del rectángulo.
- Contestar
-
El largo es de 12 y el ancho es de 8.
El perímetro de un rectángulo es 58. El largo es 5 más de tres veces el ancho. Encuentra el largo y ancho del rectángulo.
- Contestar
-
El largo es 23 y el ancho es 6.
Para Ejercicio\(\PageIndex{31}\) hay que recordar que la suma de las medidas de los ángulos de un triángulo es de 180 grados y que un triángulo rectángulo tiene un ángulo de 90 grados.
La medida de uno de los ángulos pequeños de un triángulo rectángulo es diez más de tres veces la medida del otro ángulo pequeño. Encuentra las medidas de ambos ángulos.
- Contestar
-
Dibujaremos y etiquetaremos una figura.
Paso 1. Lee el problema. 
Paso 2. Identifica lo que buscas. Estamos buscando las medidas de los ángulos. Paso 3. Nombra lo que estamos buscando. Dejar a= la medida del ángulo 1 st
b= la medida del segundo ánguloPaso 4. Traducir en un sistema de ecuaciones. La medida de uno de los ángulos pequeños
de un triángulo rectángulo es diez más de tres
veces la medida del otro ángulo pequeño.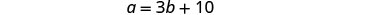
La suma de las medidas de los ángulos de
un triángulo es 180.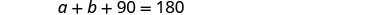
El sistema es: 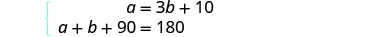
Paso 5. Resolver el sistema de ecuaciones.
Usaremos la sustitución ya que la primera
ecuación se resuelve para a.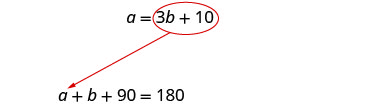
Sustituye 3 b + 10 por a en la
segunda ecuación.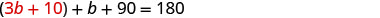
Resolver para b. 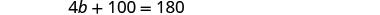


Sustituye b = 20 en la primera
ecuación y luego resuelve por a.

Paso 6. Consulta la respuesta en el problema. ¡Te lo dejaremos a ti! Paso 7. Contesta la pregunta. Las medidas de los ángulos pequeños son
20 y 70.
La medida de uno de los ángulos pequeños de un triángulo rectángulo es 2 más de 3 veces la medida del otro ángulo pequeño. Encuentra la medida de ambos ángulos.
- Responder
-
La medida de los ángulos son 22 grados y 68 grados.
La medida de uno de los ángulos pequeños de un triángulo rectángulo es 18 menos del doble de la medida del otro ángulo pequeño. Encuentra la medida de ambos ángulos.
- Responder
-
La medida de los ángulos son 36 grados y 54 grados.
A Heather se le han ofrecido dos opciones por su salario como entrenadora en el gimnasio. La opción A le pagaría $25,000 más $15 por cada sesión de entrenamiento. La opción B le pagaría $10,000 + $40 por cada sesión de entrenamiento. ¿Cuántas sesiones de capacitación harían iguales las opciones salariales?
- Responder
-
Paso 1. Lee el problema. Paso 2. Identifica lo que buscas. Estamos buscando el número de sesiones de capacitación
que hagan igual el salario.Paso 3. Nombra lo que estamos buscando. Vamos s= El salario de Heather.
n= el número de sesiones de entrenamientoPaso 4. Traducir en un sistema de ecuaciones. La opción A le pagaría $25,000 más $15
por cada sesión de entrenamiento.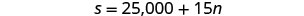
La opción B le pagaría $10,000 + $40
por cada sesión de entrenamiento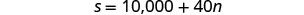
El sistema es: 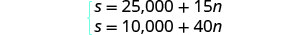
Paso 5. Resolver el sistema de ecuaciones.
Usaremos la sustitución.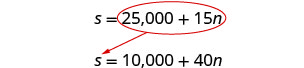
Sustituye 25,000 + 15 n por s en la segunda ecuación. 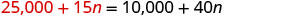
Resolver para n. 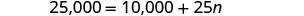
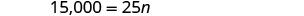

Paso 6. Consulta la respuesta. ¿Son razonables 600 sesiones de capacitación al año?
¿Las dos opciones son iguales cuando n = 600?Paso 7. Contesta la pregunta. Las opciones salariales serían iguales para 600 sesiones de capacitación.
Geraldine ha sido ofertada por dos compañías de seguros. La primera empresa paga un salario de $12,000 más una comisión de $100 por cada póliza vendida. El segundo paga un salario de 20,000 dólares más una comisión de $50 por cada póliza vendida. ¿Cuántas pólizas necesitarían venderse para que el pago total sea igual?
- Responder
-
Habría que haber 160 pólizas vendidas para que el total pague igual.
Kenneth vende actualmente trajes para la empresa A con un sueldo de $22,000 más una comisión de $10 por cada traje vendido. La compañía B le ofrece un puesto con un salario de 28,000 dólares más una comisión de $4 por cada traje vendido. ¿Cuántos trajes necesitaría Kenneth para que las opciones fueran iguales?
- Responder
-
Kenneth necesitaría vender mil trajes.
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con sistemas de resolución de ecuaciones por sustitución.
Conceptos clave
- Resolver un sistema de ecuaciones por sustitución
- Resuelve una de las ecuaciones para cualquiera de las variables.
- Sustituya la expresión del Paso 1 en la otra ecuación.
- Resuelve la ecuación resultante.
- Sustituya la solución del Paso 3 por una de las ecuaciones originales para encontrar la otra variable.
- Escribe la solución como un par ordenado.
- Comprobar que el par ordenado es una solución a ambas ecuaciones originales.


