5.3E: Ejercicios
- Page ID
- 110166
La práctica hace la perfección
Resolver un sistema de ecuaciones por eliminación
En los siguientes ejercicios, resolver los sistemas de ecuaciones por eliminación.
\(\left\{\begin{array}{l}{5 x+2 y=2} \\ {-3 x-y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+y=-9} \\ {x-2 y=-12}\end{array}\right.\)
- Contestar
-
\((6,9)\)
\(\left\{\begin{array}{l}{6 x-5 y=-1} \\ {2 x+y=13}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x-y=-7} \\ {4 x+2 y=-6}\end{array}\right.\)
- Contestar
-
\((-2,1)\)
\(\left\{\begin{array}{l}{x+y=-1} \\ {x-y=-5}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=-8} \\ {x-y=-6}\end{array}\right.\)
- Contestar
-
\((-7,-1)\)
\(\left\{\begin{array}{l}{3 x-2 y=1} \\ {-x+2 y=9}\end{array}\right.\)
\(\left\{\begin{array}{l}{-7 x+6 y=-10} \\ {x-6 y=22}\end{array}\right.\)
- Contestar
-
\((-2,-4)\)
\(\left\{\begin{array}{l}{3 x+2 y=-3} \\ {-x-2 y=-19}\end{array}\right.\)
\(\left\{\begin{array}{l}{5 x+2 y=1} \\ {-5 x-4 y=-7}\end{array}\right.\)
- Contestar
-
\((-1,3)\)
\(\left\{\begin{array}{l}{6 x+4 y=-4} \\ {-6 x-5 y=8}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x-4 y=-11} \\ {x-2 y=-5}\end{array}\right.\)
- Contestar
-
\((-1,2)\)
\(\left\{\begin{array}{l}{5 x-7 y=29} \\ {x+3 y=-3}\end{array}\right.\)
\(\left\{\begin{array}{l}{6 x-5 y=-75} \\ {-x-2 y=-13}\end{array}\right.\)
- Contestar
-
\((-5,9)\)
\(\left\{\begin{array}{l}{-x+4 y=8} \\ {3 x+5 y=10}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-5 y=7} \\ {3 x-y=17}\end{array}\right.\)
- Contestar
-
\((6,1)\)
\(\left\{\begin{array}{l}{5 x-3 y=-1} \\ {2 x-y=2}\end{array}\right.\)
\(\left\{\begin{array}{l}{7 x+y=-4} \\ {13 x+3 y=4}\end{array}\right.\)
- Contestar
-
\((-2,10)\)
\(\left\{\begin{array}{l}{-3 x+5 y=-13} \\ {2 x+y=-26}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x-5 y=-9} \\ {5 x+2 y=16}\end{array}\right.\)
- Contestar
-
\((2,3)\)
\(\left\{\begin{array}{l}{4 x-3 y=3} \\ {2 x+5 y=-31}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x+7 y=14} \\ {-2 x+3 y=32}\end{array}\right.\)
- Contestar
-
\((-7,6)\)
\(\left\{\begin{array}{l}{5 x+2 y=21} \\ {7 x-4 y=9}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x+8 y=-3} \\ {2 x+5 y=-3}\end{array}\right.\)
- Contestar
-
\((-9,3)\)
\(\left\{\begin{array}{l}{11 x+9 y=-5} \\ {7 x+5 y=-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x+8 y=67} \\ {5 x+3 y=60}\end{array}\right.\)
Contestar
-
\((9,5)\)
\(\left\{\begin{array}{l}{2 x+9 y=-4} \\ {3 x+13 y=-7}\end{array}\right.\)
\(\left\{\begin{array}{l}{\frac{1}{3} x-y=-3} \\ {x+\frac{5}{2} y=2}\end{array}\right.\)
- Contestar
-
\((-3,2)\)
\(\left\{\begin{array}{l}{x+\frac{1}{2} y=\frac{3}{2}} \\ {\frac{1}{5} x-\frac{1}{5} y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+\frac{1}{3} y=-1} \\ {\frac{1}{2} x-\frac{1}{3} y=-2}\end{array}\right.\)
- Contestar
-
\((-2,3)\)
\(\left\{\begin{array}{l}{\frac{1}{3} x-y=-3} \\ {\frac{2}{3} x+\frac{5}{2} y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x+y=3} \\ {6 x+3 y=9}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
\(\left\{\begin{array}{l}{x-4 y=-1} \\ {-3 x+12 y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x-y=8} \\ {6 x+2 y=-16}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
\(\left\{\begin{array}{l}{4 x+3 y=2} \\ {20 x+15 y=10}\end{array}\right.\)
\(\left\{\begin{array}{l}{3 x+2 y=6} \\ {-6 x-4 y=-12}\end{array}\right.\)
- Contestar
-
infinitamente muchas soluciones
\(\left\{\begin{array}{l}{5 x-8 y=12} \\ {10 x-16 y=20}\end{array}\right.\)
\(\left\{\begin{array}{l}{-11 x+12 y=60} \\ {-22 x+24 y=90}\end{array}\right.\)
- Contestar
-
inconsistente, sin solución
\(\left\{\begin{array}{l}{7 x-9 y=16} \\ {-21 x+27 y=-24}\end{array}\right.\)
\(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=\frac{5}{3} x-2}\end{array}\right.\)
- Contestar
-
inconsistente, sin solución
\(\left\{\begin{array}{l}{2 x+4 y=7} \\ {y=-\frac{1}{2} x-4}\end{array}\right.\)
Resolver Aplicaciones de Sistemas de Ecuaciones por Eliminación
En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.
La suma de dos números es 65. Su diferencia es 25. Encuentra los números.
- Contestar
-
Los números son 20 y 45.
La suma de dos números es 37. Su diferencia es de 9. Encuentra los números.
La suma de dos números es −27. Su diferencia es −59. Encuentra los números.
- Contestar
-
Los números son 16 y −43.
La suma de dos números es −45. Su diferencia es −89. Encuentra los números.
Andrea está comprando algunas playeras y suéteres nuevos. Ella es capaz de comprar 3 camisas y 2 suéteres por $114 o puede comprar 2 camisas y 4 suéteres por $164. ¿Cuánto cuesta una camisa? ¿Cuánto cuesta un suéter?
- Contestar
-
Una camisa cuesta $16 y un suéter cuesta $33.
Peter está comprando material de oficina. Es capaz de comprar 3 paquetes de papel y 4 grapadoras por $40 o puede comprar 5 paquetes de papel y 6 grapadoras por $62. ¿Cuánto cuesta un paquete de papel? ¿Cuánto cuesta una grapadora?
La cantidad total de sodio en 2 hot dogs y 3 tazas de requesón es de 4720 mg. La cantidad total de sodio en 5 hot dogs y 2 tazas de requesón es de 6300 mg. ¿Cuánto sodio hay en un hot dog? ¿Cuánto sodio hay en una taza de requesón?
- Contestar
-
Hay 860 mg en un hot dog. Hay 1,000 mg en una taza de requesón.
El número total de calorías en 2 hot dogs y 3 tazas de requesón es de 960 calorías. El número total de calorías en 5 hot dogs y 2 tazas de requesón es de 1190 calorías. ¿Cuántas calorías hay en un hot dog? ¿Cuántas calorías hay en una taza de requesón?
Elija el método más conveniente para resolver un sistema de ecuaciones lineales
En los siguientes ejercicios, decidir si sería más conveniente resolver el sistema de ecuaciones por sustitución o eliminación.
- \( \left\{\begin{array}{l}{8 x-15 y=-32} \\ {6 x+3 y=-5}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x=4 y-3} \\ {4 x-2 y=-6}\end{array}\right.\)
- Contestar
-
- eliminación
- sustitución
- \(\left\{\begin{array}{l}{y=7 x-5} \\ {3 x-2 y=16}\end{array}\right.\)
- \(\left\{\begin{array}{l}{12 x-5 y=-42} \\ {3 x+7 y=-15}\end{array}\right.\)
- \(\left\{\begin{array}{l}{y=4 x+9} \\ {5 x-2 y=-21}\end{array}\right.\)
- \(\left\{\begin{array}{l}{9 x-4 y=24} \\ {3 x+5 y=-14}\end{array}\right.\)
- Contestar
-
- sustitución
- eliminación
- \(\left\{\begin{array}{l}{14 x-15 y=-30} \\ {7 x+2 y=10}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x=9 y-11} \\ {2 x-7 y=-27}\end{array}\right.\)
Matemáticas cotidianas
En una hora Norris puede remar 3 millas río arriba contra la corriente. En la misma cantidad de tiempo puede remar 5 millas río abajo, con la corriente. Resuelve el sistema. \(\left\{\begin{array}{l}{r-c=3} \\ {r+c=5}\end{array}\right.\)
- por r, su velocidad de remo en agua sin gas.
- Entonces resuelve para c, la velocidad de la corriente del río.
- Contestar
-
- r=4
- c=1
Josie quiere hacer 10 libras de mezcla de trail usando nueces y pasas, y quiere que el costo total de la mezcla de trail sea de 54 dólares. Los frutos secos cuestan $6 por libra y las pasas cuestan $3 por libra. Resuelve el sistema\(\left\{\begin{array}{l}{n+r=10} \\ {6 n+3 r=54}\end{array}\right.\) para encontrar n, el número de libras de nueces, y rr, el número de libras de pasas que debe usar.
Ejercicios de escritura
Resolver el sistema
\(\left\{\begin{array}{l}{x+y=10} \\ {5 x+8 y=56}\end{array}\right.\)
- por sustitución
- por graficar
- ¿Qué método prefieres? ¿Por qué?
- Contestar
-
- (8, 2)
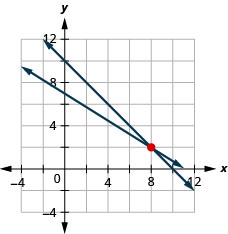
3. Las respuestas variarán.
Resolver el sistema\(\left\{\begin{array}{l}{x+y=-12} \\ {y=4-\frac{1}{2} x}\end{array}\right.\)
- por sustitución
- por graficar
- ¿Qué método prefieres? ¿Por qué?
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


