5.4: Resolver aplicaciones con sistemas de ecuaciones
- Page ID
- 110177
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Traducir a un sistema de ecuaciones
- Resolver aplicaciones de traducción directa
- Resolver aplicaciones de geometría
- Resolver aplicaciones de movimiento uniforme
Antes de comenzar, toma este cuestionario de preparación.
- La suma de dos veces por número y nueve es 31. Encuentra el número.
Si te perdiste este problema, revisa el Ejercicio 3.1.10. - Los gemelos Jon y Ron juntos ganaron 96,000 dólares el año pasado. Ron ganó $8,000 más de tres veces lo que ganó Jon. ¿Cuánto ganó cada una de las gemelas?
Si te perdiste este problema, revisa Ejercicio 3.1.31. - Alessio monta sus\(3\frac{1}{2}\) horas en bicicleta a razón de 10 millas por hora. ¿Qué tan lejos cabalgó?
Si te perdiste este problema, revisa el Ejercicio 2.6.1.
Anteriormente en este capítulo resolvimos varias aplicaciones con sistemas de ecuaciones lineales. En esta sección, veremos algunos tipos específicos de aplicaciones que relacionan dos cantidades. Traduciremos las palabras en ecuaciones lineales, decidiremos cuál es el método más conveniente de usar y luego las resolveremos.
Utilizaremos nuestra Estrategia de Resolución de Problemas para Sistemas de Ecuaciones Lineales.
UTILIZAR UNA ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS PARA SISTEMAS DE ECUACIONES LINEALES.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija variables para representar esas cantidades.
- Traducir en un sistema de ecuaciones.
- Resolver el sistema de ecuaciones utilizando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
Traducir a un Sistema de Ecuaciones
Muchos de los problemas que resolvimos en aplicaciones anteriores relacionaban dos cantidades. Estos son dos de los ejemplos del capítulo sobre Modelos matemáticos.
- La suma de dos números es de catorce negativos. Un número es cuatro menos que el otro. Encuentra los números.
- Una pareja casada gana 110 mil dólares al año. La esposa gana $16,000 menos del doble de lo que gana su esposo. ¿Qué gana el marido?
En ese capítulo traducimos cada situación en una ecuación utilizando sólo una variable. A veces era un poco difícil averiguar cómo nombrar las dos cantidades, ¿no?
Veamos cómo podemos traducir estos dos problemas en un sistema de ecuaciones con dos variables. Nos centraremos en los Pasos 1 al 4 de nuestra Estrategia de Resolución de Problemas.
Traducir a un sistema de ecuaciones:
La suma de dos números es de catorce negativos. Un número es cuatro menos que el otro. Encuentra los números.
- Contestar
-
Traducir a un sistema de ecuaciones:
La suma de dos números es negativa veintitrés. Un número es 7 menos que el otro. Encuentra los números.
- Contestar
-
\(\left\{\begin{array}{l}{m+n=-23} \\ {m=n-7}\end{array}\right.\)
Traducir a un sistema de ecuaciones:
La suma de dos números es negativa dieciocho. Un número es 40 más que el otro. Encuentra los números.
- Contestar
-
\(\left\{\begin{array}{l}{m+n=-18} \\ {m=n+40}\end{array}\right.\)
Haremos otro ejemplo donde paramos después de escribir el sistema de ecuaciones.
Traducir a un sistema de ecuaciones:
Una pareja casada gana 110 mil dólares al año. La esposa gana $16,000 menos del doble de lo que gana su esposo. ¿Qué gana el marido?
- Contestar
-
\(\begin{array}{ll}{\text {We are looking for the amount that }} & {\text {Let } h=\text { the amount the husband earns. }} \\ {\text {the husband and wife each earn. }} & { w=\text { the amount the wife earns }} \\ {\text{Translate.}} & {\text{A married couple together earns \$110,000.} }\\ {} & {w+h=110000} \\ & \text{The wife earns \$16,000 less than twice what} \\ & \text{husband earns.} \\ & w=2h−16,000 \\ \text{The system of equations is:} & \left\{\begin{array}{l}{w+h=110,000} \\ {w=2 h-16,000}\end{array}\right.\end{array}\)
Traducir a un sistema de ecuaciones:
Una pareja tiene un ingreso familiar total de 84,000 dólares. El esposo gana $18,000 menos del doble de lo que gana la esposa. ¿Cuánto gana la esposa?
- Contestar
-
\(\left\{\begin{array}{l}{w+h=84,000} \\ {h=2 w-18,000}\end{array}\right.\)
Traducir a un sistema de ecuaciones:
Un empleado senior gana $5 menos del doble de lo que gana un nuevo empleado por hora. Juntos hacen 43 dólares por hora. ¿Cuánto gana cada empleado por hora?
- Contestar
-
\(\left\{\begin{array}{l}{s=2 n-5} \\ {s+n=43}\end{array}\right.\)
Resolver aplicaciones de traducción directa
Establecimos, pero no resolvimos, los sistemas de ecuaciones en Ejercicio\(\PageIndex{1}\) y Ejercicio\(\PageIndex{4}\) Ahora traduciremos una situación a un sistema de ecuaciones y luego la resolveremos.
Traduzca a un sistema de ecuaciones y luego resuelva:
Devon es 26 años mayor que su hijo Cooper. La suma de sus edades es de 50 años. Encuentra sus edades.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. Buscamos las edades de Devon y Cooper. Paso 3. Nombra lo que estamos buscando. Deja que d= la edad de Devon.
c= Edad de CooperPaso 4. Traducir en un sistema de ecuaciones. Devon es 26 años mayor que Cooper.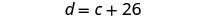 
La suma de sus edades es de 50 años.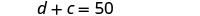 
El sistema es: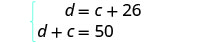 
Paso 5. Resolver el sistema de ecuaciones.
Resolver por sustitución.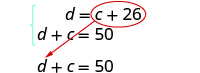
Sustituir c + 26 en la segunda ecuación.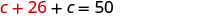 
Resolver para c.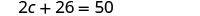 
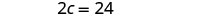
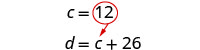
Sustituye c = 12 en la primera ecuación y luego resuelve para d. 
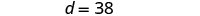
Paso 6. Consulta la respuesta en el problema. ¿La edad de Devon es 26 más que la de Cooper?
Sí, 38 es 26 más que 12.
¿La suma de sus edades es de 50?
Sí, 38 más 12 es 50.Paso 7. Contesta la pregunta. Devon tiene 38 años y Cooper tiene 12 años.
Traduzca a un sistema de ecuaciones y luego resuelva:
Ali es 12 años mayor que su hermana menor, Jameela. La suma de sus edades es de 40. Encuentra sus edades.
- Contestar
-
Ali tiene 26 años y Jameela tiene 14.
Traduzca a un sistema de ecuaciones y luego resuelva:
El papá de Jake tiene 6 más de 3 veces la edad de Jake. La suma de sus edades es de 42 años. Encuentra sus edades.
- Contestar
-
Jake tiene 9 y su papá 33.
Traduzca a un sistema de ecuaciones y luego resuelva:
Cuando Jenna pasó 10 minutos en el entrenador elíptico y luego hizo entrenamiento de circuito durante 20 minutos, su aplicación de fitness dice que quemó 278 calorías. Cuando pasó 20 minutos en el entrenador elíptico y 30 minutos de entrenamiento de circuito quemó 473 calorías. ¿Cuántas calorías quema por cada minuto en el entrenador elíptico? ¿Cuántas calorías quema por cada minuto de entrenamiento en circuito?
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. Estamos buscando la cantidad de
calorías quemadas cada minuto en el entrenador
elíptico y cada minuto de entrenamiento de
circuito.Paso 3. Nombra lo que estamos buscando. Dejar e= número de calorías quemadas por minuto en el entrenador elíptico.
c= número de calorías quemadas por minuto durante el entrenamiento de circuitoPaso 4. Traducir en un sistema de ecuaciones. 10 minutos en la elíptica y
entrenamiento de circuito durante 20 minutos, quemó
278 calorías
20 minutos en la elíptica y
30 minutos de entrenamiento de circuito quemaron
473 calorías
El sistema es: 
Paso 5. Resolver el sistema de ecuaciones. Multiplica la primera ecuación por −2 para obtener coeficientes opuestos de e.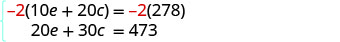 
Simplifica y suma las ecuaciones.
Resolver para c.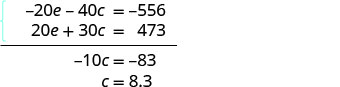
Sustituye c = 8.3 en una de las ecuaciones originales para resolver por e. 
Paso 6. Consulta la respuesta en el problema. Comprueba las matemáticas por tu cuenta.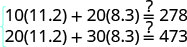 
Paso 7. Contesta la pregunta. Jenna quema 8.3 calorías por minuto de entrenamiento en
circuito y 11.2 calorías por
minuto mientras está en el entrenador elíptico.
Traduzca a un sistema de ecuaciones y luego resuelva:
Mark fue al gimnasio e hizo 40 minutos de yoga caliente Bikram y 10 minutos de saltos de jacks. Quemó 510 calorías. La siguiente vez que fue al gimnasio, hizo 30 minutos de yoga caliente Bikram y 20 minutos de jacks saltando quemando 470 calorías. ¿Cuántas calorías se quemaron por cada minuto de yoga? ¿Cuántas calorías se quemaron por cada minuto de saltos?
- Contestar
-
Mark quemó 11 calorías por cada minuto de yoga y 7 calorías por cada minuto de saltos.
Traduzca a un sistema de ecuaciones y luego resuelva:
Erin pasó 30 minutos en la máquina de remo y 20 minutos levantando pesas en el gimnasio y quemó 430 calorías. Durante su siguiente visita al gimnasio pasó 50 minutos en la máquina de remo y 10 minutos levantando pesas y quemando 600 calorías. ¿Cuántas calorías quemó por cada minuto en la máquina de remo? ¿Cuántas calorías quemó por cada minuto de levantamiento de pesas?
- Contestar
-
Erin quemó 11 calorías por cada minuto en la máquina de remo y 5 calorías por cada minuto de levantamiento de pesas.
Resolver aplicaciones de geometría
Cuando aprendimos sobre Modelos Matemáticos, resolvimos aplicaciones de geometría usando propiedades de triángulos y rectángulos. Ahora agregaremos a nuestra lista algunas propiedades de ángulos.
Las medidas de dos ángulos complementarios suman 90 grados. Las medidas de dos ángulos suplementarios suman 180 grados.
Dos ángulos son complementarios si la suma de las medidas de sus ángulos es de 90 grados.
Dos ángulos son suplementarios si la suma de las medidas de sus ángulos es de 180 grados.
Si dos ángulos son complementarios, decimos que un ángulo es el complemento del otro.
Si dos ángulos son complementarios, decimos que un ángulo es el suplemento del otro.
Traduzca a un sistema de ecuaciones y luego resuelva:
La diferencia de dos ángulos complementarios es de 26 grados. Encuentra las medidas de los ángulos.
- Contestar
-
\(\begin{array}{ll}{\textbf {Step 1. Read}\text{ the problem. }} & {} \\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} & {\text {We are looking for the measure of each angle.}} \\ \\ {\textbf{Step 3. Name}\text{ what we are looking for.}} & {\text{Let x = the measure of the first angle.} }\\ {} & \text{y = the measure of the second angle} \\ \textbf{Step 4. Translate}\text{ into a system of equations.}& \text{The angles are complementary.} \\ & \text{x+y=90} \\ & \text{The difference of the two angles is 26 degrees.} \\ & \text{x−y=26} \\ \\ \text{The system is} & {\left\{\begin{array}{l}{x+y=90} \\ {x-y=26}\end{array}\right.} \\ \textbf{Step 5. Solve}\text{ the system of equations by elimination.} \\& \left\{\begin{array}{l}{x+y=90} \\ \underline{x-y=26}\end{array}\right. \\ & \quad2x\quad=116 \\ \text{Substitute x = 58 into the first equation.}& \begin{array}{lrll} &x&=&58 \\ &x+y&=&90 \\ &58+y&=&90 \\ &y&=&32\end{array} \\ \textbf{Step 6. Check}\text{ the answer in the problem.} & \\ 58+32=90\checkmark\\ 58-32=36\checkmark \\ \\ \textbf{Step 7. Answer}\text{ the question.} & \text{The angle measures are 58 degrees and 32 degrees.}\end{array}\)
Traduzca a un sistema de ecuaciones y luego resuelva:
La diferencia de dos ángulos complementarios es de 20 grados. Encuentra las medidas de los ángulos.
- Contestar
-
Las medidas del ángulo son 55 grados y 35 grados.
Traduzca a un sistema de ecuaciones y luego resuelva:
La diferencia de dos ángulos complementarios es de 80 grados. Encuentra las medidas de los ángulos.
- Contestar
-
Las medidas del ángulo son de 5 grados y 85 grados.
Traduzca a un sistema de ecuaciones y luego resuelva:
Dos ángulos son suplementarios. La medida del ángulo mayor es doce grados menos de cinco veces la medida del ángulo más pequeño. Encuentra las medidas de ambos ángulos.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identificar lo que estamos buscando. Estamos buscando la medida de cada ángulo. Paso 3. Nombra lo que estamos buscando. Dejar x= la medida del primer ángulo.
y= la medida del segundo ánguloPaso 4. Traducir en un sistema de ecuaciones. Los ángulos son suplementarios. 
El ángulo más grande es doce menos de cinco veces el ángulo más pequeño 
El sistema es:
Paso 5. Resolver el sistema de sustitución de ecuaciones.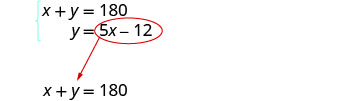
Sustituye 5 x − 12 por y en la primera ecuación. 
Resolver para x. 
Sustituye 32 por en la segunda ecuación, luego resuelve por y.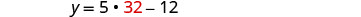 
Paso 6. Consulta la respuesta en el problema.
\(\begin{aligned} 32+158 &=180 \checkmark \\ 5 \cdot 32-12 &=147 \checkmark \end{aligned}\)Paso 7. Contesta la pregunta. Las medidas del ángulo son 148 y 32.
Traduzca a un sistema de ecuaciones y luego resuelva:
Dos ángulos son suplementarios. La medida del ángulo mayor es de 12 grados más de tres veces el ángulo más pequeño. Encuentra las medidas de los ángulos.
- Contestar
-
Las medidas del ángulo son 42 grados y 138 grados.
Traduzca a un sistema de ecuaciones y luego resuelva:
Dos ángulos son suplementarios. La medida del ángulo mayor es 18 menos del doble de la medida del ángulo más pequeño. Encuentra las medidas de los ángulos.
- Contestar
-
Las medidas del ángulo son 66 grados y 114 grados.
Traduzca a un sistema de ecuaciones y luego resuelva:
Randall tiene 125 pies de esgrima para encerrar la parte rectangular de su patio trasero adyacente a su casa. Sólo necesitará cercar alrededor de tres lados, porque el cuarto lado será la pared de la casa. Quiere que la longitud del patio cercado (paralelo a la pared de la casa) sea 5 pies más de cuatro veces más de largo que el ancho. Encuentra el largo y el ancho.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identifica lo que buscas. Estamos buscando el largo y ancho.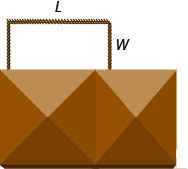 
Paso 3. Nombra lo que estamos buscando. Deje L= la longitud del patio cercado.
W= el ancho del patio cercadoPaso 4. Traducir en un sistema de ecuaciones. Una longitud y dos anchos equivalen a 125.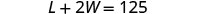 
La longitud será de 5 pies más de cuatro veces el ancho.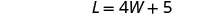 
El sistema es:
Paso 5. Resolver el sistema de ecuaciones por sustitución.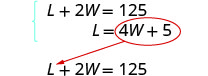
Sustituye L = 4 W + 5 en la primera
ecuación, luego resuelve para W.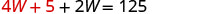
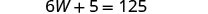
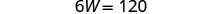
Sustituye 20 por W en la segunda
ecuación, luego resuelve por L.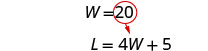
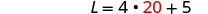
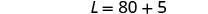
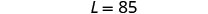
Paso 6. Consulta la respuesta en el problema.
\(\begin{array}{rll} 20+28+20&=&125\checkmark \\ 85 &=&4\cdot 20 + 5\checkmark\end{array}\)Paso 7. Contesta la ecuación. La longitud es de 85 pies y el ancho es de 20 pies.
Traduzca a un sistema de ecuaciones y luego resuelva:
Mario quiere poner una barda rectangular alrededor de la alberca en su patio trasero. Dado que un lado es adyacente a la casa, solo necesitará cercar tres lados. Hay dos lados largos y el lado más corto es paralelo a la casa. Necesita 155 pies de esgrima para encerrar la alberca. La longitud del lado largo es de 10 pies menos del doble de ancho. Encuentra el largo y ancho del área de la piscina que se va a encerrar.
- Contestar
-
La longitud es de 60 pies y el ancho es de 35 pies.
Traduzca a un sistema de ecuaciones y luego resuelva:
Alexis quiere construir una corrida rectangular para perros en su patio adyacente a la barda de su vecina. Ella usará 136 pies de esgrima para encerrar completamente la carrera de perros rectangular. La longitud del perro que corre a lo largo de la cerca del vecino será de 16 pies menos que el doble de ancho. Encuentra el largo y ancho de la carrera para perros.
- Contestar
-
La longitud es de 60 pies y el ancho es de 38 pies.
Resolver aplicaciones de movimiento uniforme
Usamos una tabla para organizar la información en problemas de movimiento uniforme cuando los presentamos antes. Seguiremos usando la tabla aquí. La ecuación básica fue D = rt donde D es la distancia recorrida, r es la velocidad y t es el tiempo.
Nuestro primer ejemplo de una aplicación de movimiento uniforme será para una situación similar a algunas que ya hemos visto, pero ahora podemos usar dos variables y dos ecuaciones.
Traduzca a un sistema de ecuaciones y luego resuelva:
Joni salió de St. Louis por la interestatal, conduciendo hacia el oeste hacia Denver a una velocidad de 65 millas por hora. Media hora después, Kelly salió de St. Louis en la misma ruta que Joni, manejando 78 millas por hora. ¿Cuánto tiempo le tomará a Kelly ponerse al día con Joni?
- Contestar
-
Un diagrama es útil para ayudarnos a visualizar la situación.
Identificar y nombrar lo que estamos buscando.
Un gráfico nos ayudará a organizar los datos.
Conocemos las tarifas tanto de Joni como de Kelly, y así las
ingresamos en el gráfico.Estamos buscando el tiempo que Kelly,
k, y Joni, j, conducirán cada uno.
Desde d=R·t podemos rellenar la columna Distancia.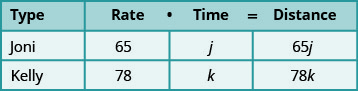
Traducir en un sistema de ecuaciones.
Para hacer el sistema de ecuaciones, debemos reconocer que Kelly y Joni recorrerán la misma distancia. Entonces, 65j=78k.
Además, dado que Kelly se fue más tarde, su tiempo será 1212 horas menos que el tiempo de Joni.
Entonces, k=j−12.Ahora tenemos el sistema.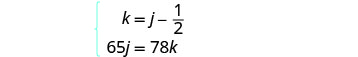 
Resolver el sistema de ecuaciones por sustitución.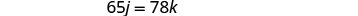 
Sustituye k=j−12 en la segunda ecuación, luego resuelve para j.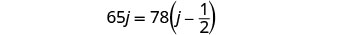 
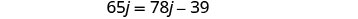
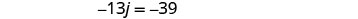
Para encontrar el tiempo de Kelly, sustituya j = 3 en la primera ecuación, luego resuelva por k.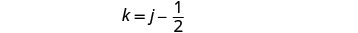 
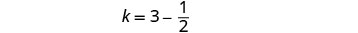
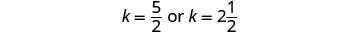
Consulta la respuesta en el problema.
Joni 3 horas (65 mph) = 195 millas.
Kelly\(2\frac{1}{2}\) horas (78 mph) = 195 millas.
Sí, habrán recorrido la misma distancia
cuando se encuentren.Contesta la pregunta. Kelly alcanzará a Joni en\(2\frac{1}{2}\) horas.
Para entonces, Joni habrá viajado 3 horas.
Traduzca a un sistema de ecuaciones y luego resuelva: Mitchell salió de Detroit en la interestatal conduciendo hacia el sur hacia Orlando a una velocidad de 60 millas por hora. Clark salió de Detroit 1 hora después viajando a una velocidad de 75 millas por hora, siguiendo la misma ruta que Mitchell. ¿Cuánto tardará Clark en atrapar a Mitchell?
- Contestar
-
Clark tardará 4 horas en atrapar a Mitchell.
Traduzca a un sistema de ecuaciones y luego resuelva: Charlie salió de la casa de su madre viajando a una velocidad promedio de 36 millas por hora. Su hermana Sally salió 15 minutos (1/4 hora) después recorriendo la misma ruta a una velocidad promedio de 42 millas por hora. ¿Cuánto falta para que Sally alcance a Charlie?
- Contestar
-
Sally tardará\(1\frac{1}{2}\) horas en ponerse al día con Charlie.
Muchas aplicaciones del mundo real del movimiento uniforme surgen debido a los efectos de las corrientes, de agua o aire, en la velocidad real de un vehículo. Los vuelos de avión a campo traviesa en Estados Unidos suelen tardar más tiempo yendo hacia el oeste que hacia el este debido a las corrientes de viento predominantes.
Echemos un vistazo a un barco que viaja por un río. Dependiendo de qué dirección vaya la embarcación, la corriente del agua o la está ralentizando o acelerando.
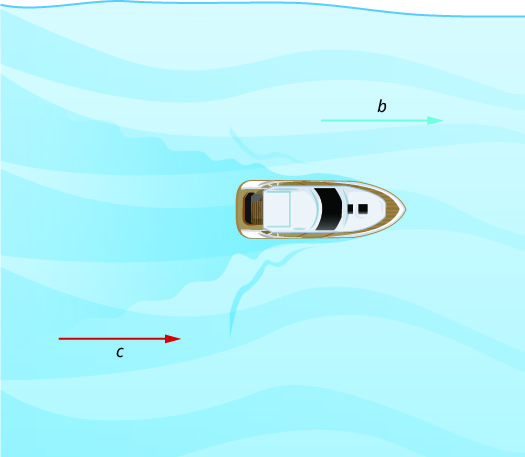
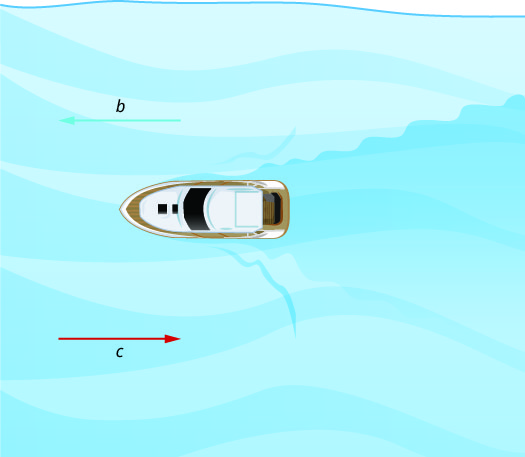
La figura\(\PageIndex{1}\) y la figura\(\PageIndex{2}\) muestran cómo la corriente de un río afecta la velocidad a la que realmente viaja una embarcación. Llamaremos a la velocidad de la embarcación en aguas tranquilas b y a la velocidad del río corriente c.
En\(\PageIndex{1}\) la Figura la embarcación va aguas abajo, en la misma dirección que la corriente del río. La corriente ayuda a empujar la embarcación, por lo que la velocidad real de la embarcación es más rápida que su velocidad en aguas tranquilas. La velocidad real a la que se mueve la embarcación es b + c.
En Figura\(\PageIndex{2}\) la embarcación va aguas arriba, frente a la corriente del río. La corriente va en contra de la embarcación, por lo que la velocidad real de la embarcación es más lenta que su velocidad en aguas tranquilas. La velocidad real de la embarcación es b−c.
Pondremos algunos números a esta situación en Ejercicio\(\PageIndex{25}\).
Traduzca a un sistema de ecuaciones y luego resuelva:
Un crucero fluvial navegó 60 millas río abajo durante 4 horas y luego tardó 5 horas navegando río arriba para regresar al muelle. Encuentra la velocidad del barco en aguas tranquilas y la velocidad de la corriente del río.
- Contestar
-
Lee el problema.
Este es un problema de movimiento uniforme y una imagen nos ayudará a visualizar la situación.
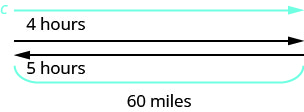
Identificar lo que estamos buscando. Estamos buscando la velocidad del barco
en aguas tranquilas y la velocidad de la corriente.Nombra lo que estamos buscando. Dejar s=s= la tasa de la nave en agua sin gas.
c=c= la tasa de la corrienteUn gráfico nos ayudará a organizar la información.
El barco va aguas abajo y luego aguas arriba.
Al ir río abajo, la corriente ayuda al
barco; por lo tanto, la tasa real del barco es s + c.
Al ir aguas arriba, la corriente ralentiza el barco;
por lo tanto, la tasa real es s − c.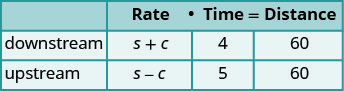
Aguas abajo toma 4 horas.
Upstream toma 5 horas.
En cada sentido la distancia es de 60 millas.Traducir en un sistema de ecuaciones.
Dado que los tiempos de tasa el tiempo es distancia, podemos
escribir el sistema de ecuaciones.
Resolver el sistema de ecuaciones.
Distribuir para poner ambas ecuaciones en
forma estándar, luego resolver por eliminación.
Multiplique la ecuación superior por 5 y la ecuación inferior por 4.
Agregue las ecuaciones, luego resuelva para s.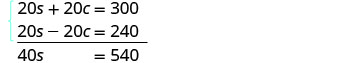
Sustituir s = 13.5 en una de las ecuaciones originales. 
Consulta la respuesta en el problema.
La velocidad aguas abajo sería
13.5 + 1.5 = 15 mph.
En 4 horas el barco viajaría
15 · 4 = 60 millas.
La tasa ascendente sería
13.5 − 1.5 = 12 mph.
En 5 horas el barco viajaría
12 · 5 = 60 millas.Contesta la pregunta. La tasa del barco es de 13.5 mph y
la tasa de la corriente es 1.5 mph.
Traduzca a un sistema de ecuaciones y luego resuelva: Un crucero en barco por el río Mississippi navegó 120 millas río arriba durante 12 horas y luego tardó 10 horas en regresar al muelle. Encuentra la velocidad del barco fluvial en aguas tranquilas y la velocidad de la corriente del río.
- Contestar
-
La tasa de la embarcación es de 11 mph y la tasa de la corriente es de 1 mph.
Traduzca a un sistema de ecuaciones y luego resuelva: Jason remó su canoa 24 millas río arriba durante 4 horas. Le tomó 3 horas remar hacia atrás. Encuentra la velocidad de la canoa en aguas tranquilas y la velocidad de la corriente del río.
- Contestar
-
La velocidad de la canoa es de 7 mph y la velocidad de la corriente es de 1 mph.
Las corrientes de viento afectan las velocidades de los aviones de la misma manera que las corrientes de agua afectan a las velocidades Veremos esto en Ejercicio\(\PageIndex{28}\). Una corriente de viento en la misma dirección en la que vuela el avión se llama viento de cola. Una corriente de viento que sopla contra la dirección del avión se llama viento en contra.
Traduzca a un sistema de ecuaciones y luego resuelva:
Un jet privado puede volar 1095 millas en tres horas con viento de cola pero solo 987 millas en tres horas en viento en contra. Encuentra la velocidad del jet en aire quieto y la velocidad del viento.
- Contestar
-
Lee el problema.
Este es un problema de movimiento uniforme y una imagen nos ayudará a visualizar.
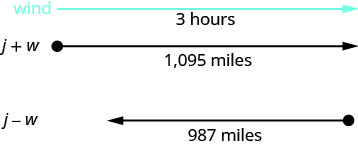
Identificar lo que estamos buscando. Estamos buscando la velocidad del jet
en aire quieto y la velocidad del viento.Nombra lo que estamos buscando. Deja que j= la velocidad del jet en aire quieto.
w= la velocidad del vientoUn gráfico nos ayudará a organizar la información.
El jet realiza dos viajes, uno en viento de cola
y otro en viento en contra.
En un viento de cola, el viento ayuda al jet y así
la velocidad es j + w.
En un viento en contra, el viento ralentiza el jet y
así la velocidad es j − w.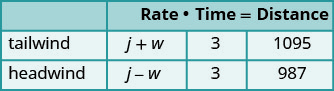
Cada viaje dura 3 horas.
En un viento de cola el jet vuela 1095 millas.
En viento en contra el jet vuela 987 millas.Traducir en un sistema de ecuaciones.
Dado que los tiempos de tasa el tiempo es distancia, obtenemos el
sistema de ecuaciones.
Resolver el sistema de ecuaciones.
Distribuir, luego resolver por eliminación.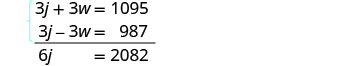
Agregar, y resolver para j.
Sustituye j = 347 en una de las
ecuaciones originales, luego resuelve para w.
Consulta la respuesta en el problema.
Con el viento de cola, la velocidad real del
jet sería
347 + 18 = 365 mph.
En 3 horas el jet viajaría
365 · 3 = 1095 millas.
Al entrar en el viento en contra, la
tasa real del jet sería
347 − 18 = 329 mph.
En 3 horas el jet viajaría
329 · 3 = 987 millas.Contesta la pregunta. La velocidad del jet es de 347 mph y la
velocidad del viento es de 18 mph.
Traduzca a un sistema de ecuaciones y luego resuelva: Un jet pequeño puede volar 1,325 millas en 5 horas con viento de cola pero solo 1025 millas en 5 horas en viento en contra. Encuentra la velocidad del jet en aire quieto y la velocidad del viento.
- Contestar
-
La velocidad del jet es de 235 mph y la velocidad del viento es de 30 mph.
Traduzca a un sistema de ecuaciones y luego resuelva: Un jet comercial puede volar 1728 millas en 4 horas con viento de cola pero solo 1536 millas en 4 horas en viento en contra. Encuentra la velocidad del jet en aire quieto y la velocidad del viento.
- Contestar
-
La velocidad del jet es de 408 mph y la velocidad del viento es de 24 mph.
Glosario
- ángulos complementarios
- Dos ángulos son complementarios si la suma de las medidas de sus ángulos es\(90\) grados.
- ángulos suplementarios
- Dos ángulos son suplementarios si la suma de las medidas de sus ángulos es\(180\) grados.