5.3: Resolver sistemas de ecuaciones por eliminación

Objetivos de aprendizaje

Al final de esta sección, podrás:

• Resolver un sistema de ecuaciones por eliminación
• Resolver aplicaciones de sistemas de ecuaciones por eliminación
• Elija el método más conveniente para resolver un sistema de ecuaciones lineales

Nota

Antes de comenzar, toma este cuestionario de preparación.

1. Simplifique −5 (6−3a).
   Si te perdiste este problema, revisa Ejercicio 1.10.43.
2. Resuelve la ecuación\(\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}\).
   Si te perdiste este problema, revisa el Ejercicio 2.5.1.

Hemos resuelto sistemas de ecuaciones lineales mediante gráficas y por sustitución. La gráfica funciona bien cuando los coeficientes variables son pequeños y la solución tiene valores enteros. La sustitución funciona bien cuando podemos resolver fácilmente una ecuación para una de las variables y no tener demasiadas fracciones en la expresión resultante.

El tercer método de resolución de sistemas de ecuaciones lineales se llama Método de Eliminación. Cuando resolvimos un sistema por sustitución, comenzamos con dos ecuaciones y dos variables y lo redujimos a una ecuación con una variable. Esto es lo que haremos con el método de eliminación, también, pero tendremos una manera diferente de llegar ahí.

Resolver un sistema de ecuaciones por eliminación

El Método de Eliminación se basa en la Propiedad de Adición de Igualdad. El Adición Propiedad de Igualdad dice que cuando se agrega la misma cantidad a ambos lados de una ecuación, todavía se tiene igualdad. Ampliaremos la Propiedad de Suma de Igualdad para decir que cuando se agregan cantidades iguales a ambos lados de una ecuación, los resultados son iguales.

Para cualquier expresión a, b, c y d,

\[\begin{array}{lc} \text{ if } & a=b \\ \text { and } & c=d \\ \text { then } &a+c =b+d \end{array}\]

Para resolver un sistema de ecuaciones por eliminación, comenzamos con ambas ecuaciones en forma estándar. Entonces decidimos qué variable será la más fácil de eliminar. ¿Cómo decidimos? Queremos que los coeficientes de una variable sean opuestos, para que podamos sumar las ecuaciones y eliminar esa variable.

Observe cómo funciona eso cuando sumamos estas dos ecuaciones juntas:

\[\begin{array}{l} 3x+y=5 \\ \underline{2x-y=0} \\ 5x\quad\quad=5\end{array}\]

Las y se suman a cero y tenemos una ecuación con una variable.

Probemos otro:

\[\left\{\begin{array}{l}{x+4 y=2} \\ {2 x+5 y=-2}\end{array}\right.\]

Esta vez no vemos una variable que pueda ser eliminada de inmediato si sumamos las ecuaciones.

Pero si multiplicamos la primera ecuación por −2, haremos los coeficientes de x opuestos. Debemos multiplicar cada término en ambos lados de la ecuación por −2.

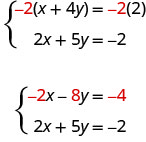
Ahora vemos que los coeficientes de los términos x son opuestos, por lo que x se eliminará cuando agreguemos estas dos ecuaciones.

Agrega las ecuaciones tú mismo: el resultado debe ser −3 y = −6. Y eso parece fácil de resolver, ¿no? Así es como se vería.

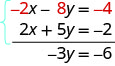
Haremos una más:

\[\left\{\begin{array}{l}{4 x-3 y=10} \\ {3 x+5 y=-7}\end{array}\right.\]

No parece que podamos conseguir que los coeficientes de una variable sean opuestos multiplicando una de las ecuaciones por una constante, a menos que usemos fracciones. Entonces, en cambio, tendremos que multiplicar ambas ecuaciones por una constante.

Podemos hacer que los coeficientes de x sean opuestos si multiplicamos la primera ecuación por 3 y la segunda por −4, así obtenemos 12 x y −12 x.

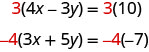
Esto nos da estas dos nuevas ecuaciones:

\[\left\{\begin{aligned} 12 x-9 y &=30 \\-12 x-20 y &=28 \end{aligned}\right.\]

Cuando añadimos estas ecuaciones,

\[\[\left\{\begin{array}{r}{12 x-9 y=30} \\ {\underline{-12 x-20 y=28}} \\\end{array}\right.\\\quad\qquad {-29 y=58}\]\]

se eliminan las x y solo tenemos −29 y = 58.

Una vez que obtenemos una ecuación con una sola variable, la resolvemos. Luego sustituimos ese valor en una de las ecuaciones originales para resolver por la variable restante. Y, como siempre, verificamos nuestra respuesta para asegurarnos de que sea una solución a ambas ecuaciones originales.

Ahora veremos cómo usar la eliminación para resolver el mismo sistema de ecuaciones que resolvimos graficando y por sustitución.

Ejercicio\(\PageIndex{1}\): How to Solve a System of Equations by Elimination

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)

Contestar

Ejercicio\(\PageIndex{2}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x-3 y=7}\end{array}\right.\)

Contestar

(2, −1)

Ejercicio\(\PageIndex{3}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{4 x+y=-5} \\ {-2 x-2 y=-2}\end{array}\right.\)

Contestar

(−2,3)

Los pasos se enumeran a continuación para una fácil referencia.

COMO RESOLVER UN SISTEMA DE ECUACIONES POR ELIMINACIÓN.

1. Escribe ambas ecuaciones en forma estándar. Si alguno de los coeficientes son fracciones, límpielos.
2. Hacer los coeficientes de una variable opuestos.
   • Decide qué variable vas a eliminar.
   • Multiplique una o ambas ecuaciones para que los coeficientes de esa variable sean opuestos.
3. Agregue las ecuaciones resultantes del Paso 2 para eliminar una variable.
4. Resolver para la variable restante.
5. Sustituir la solución del Paso 4 por una de las ecuaciones originales. Entonces resuelve para la otra variable.
6. Escribe la solución como un par ordenado.
7. Comprobar que el par ordenado es una solución a ambas ecuaciones originales.

Primero haremos un ejemplo donde podemos eliminar una variable de inmediato.

Ejercicio\(\PageIndex{4}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{x+y=10} \\ {x-y=12}\end{array}\right.\)

Contestar

Ambas ecuaciones están en forma estándar.
Los coeficientes de y ya son opuestos.
Sumar las dos ecuaciones para eliminar y. La ecuación resultante tiene sólo 1 variable, x.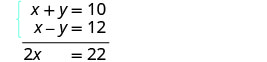
Resuelve para x, la variable restante. Sustituye x = 11 en una de las ecuaciones originales.
Resolver para la otra variable, y.
Escribe la solución como un par ordenado.	El par ordenado es (11, −1).
Comprobar que el par ordenado es una solución a ambas ecuaciones originales. \(\begin{array}{rllrll} x+y &=&10 &x-y&=&12\\ 11+(-1) &\stackrel{?}{=}&10 & 11-(-1) &\stackrel{?}{=}&12\\ 10 &=&10 \checkmark & 12 &=&12 \checkmark \end{array}\)
	La solución es (11, −1).

Ejercicio\(\PageIndex{5}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{2 x+y=5} \\ {x-y=4}\end{array}\right.\)

Contestar

(3, −1)

Ejercicio\(\PageIndex{6}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{x+y=3} \\ {-2 x-y=-1}\end{array}\right.\)

Contestar

(−2,5)

En Ejercicio\(\PageIndex{7}\), podremos hacer los coeficientes de una variable opuestos multiplicando una ecuación por una constante.

Ejercicio\(\PageIndex{7}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{3 x-2 y=-2} \\ {5 x-6 y=10}\end{array}\right.\)

Contestar

Ambas ecuaciones están en forma estándar.
Ninguno de los coeficientes son opuestos.
Podemos hacer los coeficientes de y opuestos multiplicando la primera ecuación por −3.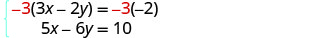
Simplificar.
Sumar las dos ecuaciones para eliminar y.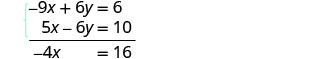
Resolver para la variable restante, x. Sustituye x = −4 en una de las ecuaciones originales.
Resolver por y.
Escribe la solución como un par ordenado.	El par ordenado es (−4, −5).
Comprobar que el par ordenado es una solución a ambas ecuaciones originales. \(\begin{array}{rllrll} 3x-2y &=&-2 &5x-6y&=&10\\ 3(-4)-2(-5) &\stackrel{?}{=}&-2 & 5(-4)-6(-5) &\stackrel{?}{=}&10\\ -12+10&\stackrel{?}{=}&-2 &-20+30&\stackrel{?}{=}&10\\-2 &=&-2 \checkmark & 10 &=&10 \checkmark \end{array}\)
	La solución es (−4, −5).

Ejercicio\(\PageIndex{8}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{4 x-3 y=1} \\ {5 x-9 y=-4}\end{array}\right.\)

Contestar

(1,1)

Ejercicio\(\PageIndex{9}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{3 x+2 y=2} \\ {6 x+5 y=8}\end{array}\right.\)

Contestar

(−2,4)

Ahora vamos a hacer un ejemplo donde necesitamos multiplicar ambas ecuaciones por constantes para hacer los coeficientes de una variable opuestos.

Ejercicio\(\PageIndex{10}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{4 x-3 y=9} \\ {7 x+2 y=-6}\end{array}\right.\)

Contestar

En este ejemplo, no podemos multiplicar una sola ecuación por cualquier constante para obtener coeficientes opuestos. Entonces vamos a multiplicar estratégicamente ambas ecuaciones por una constante para obtener los opuestos.

Ambas ecuaciones están en forma estándar. Para obtener coeficientes opuestos de y, multiplicaremos la primera ecuación por 2 y la segunda por 3.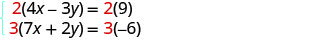
Simplificar.
Sumar las dos ecuaciones para eliminar y.
Resolver para x. Sustituye x = 0 en una de las ecuaciones originales.
Resolver por y.
Escribe la solución como un par ordenado.	El par ordenado es (0, −3).
Comprobar que el par ordenado es una solución a ambas ecuaciones originales. \(\begin{array}{rllrll} 4x-3y &=&9 &7x+2y&=&-6\\ 4(0)-3(-3) &\stackrel{?}{=}&9 & 7(0)+2(-3) &\stackrel{?}{=}&-6\\9 &=&9 \checkmark & -6 &=&-6 \checkmark \end{array}\)
	La solución es (0, −3).

Ejercicio\(\PageIndex{11}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)

Contestar

(1,3)

Ejercicio\(\PageIndex{12}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{7 x+8 y=4} \\ {3 x-5 y=27}\end{array}\right.\)

Contestar

(4, −3)

Cuando el sistema de ecuaciones contenga fracciones, primero limpiaremos las fracciones multiplicando cada ecuación por su LCD.

Ejercicio\(\PageIndex{13}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{x+\frac{1}{2} y=6} \\ {\frac{3}{2} x+\frac{2}{3} y=\frac{17}{2}}\end{array}\right.\)

Contestar

En este ejemplo, ambas ecuaciones tienen fracciones. Nuestro primer paso será multiplicar cada ecuación por su LCD para borrar las fracciones.

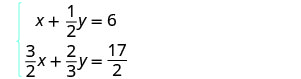
Para borrar las fracciones, multiplica cada ecuación por su LCD.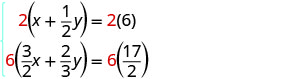
Simplificar.
Ahora estamos listos para eliminar una de las variables. Observe que ambas ecuaciones están en forma estándar.
Podemos eliminar y multiplicando la ecuación superior por −4.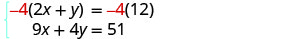
Simplificar y agregar. Sustituye x = 3 en una de las ecuaciones originales.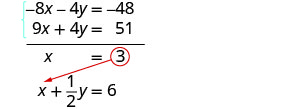
Resolver por y.
Escribe la solución como un par ordenado.	El par ordenado es (3, 6).
Comprobar que el par ordenado es una solución a ambas ecuaciones originales. \(\begin{array}{rllrll} x+\frac{1}{2}y &=&6 &\frac{3}{2}x+\frac{2}{3}y&=&\frac{17}{2}\\ 3+\frac{1}{2}(6) &\stackrel{?}{=}&6 &\frac{3}{2}(3) + \frac{2}{3}(6)&\stackrel{?}{=}&\frac{17}{2}\\ 3 + 3 &\stackrel{?}{=}&6 & \frac{9}{2 }+4 &\stackrel{?}{=} & \frac{17}{2}\\ 6 &=&6 \checkmark & \frac{9}{2} + \frac{8}{2} &\stackrel{?}{=} & \frac{17}{2}\\ && & \frac{17}{2} &=&\frac{17}{2} \checkmark \end{array}\)
	La solución es (3, 6).

Ejercicio\(\PageIndex{14}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{\frac{1}{3} x-\frac{1}{2} y=1} \\ {\frac{3}{4} x-y=\frac{5}{2}}\end{array}\right.\)

Contestar

(6,2)

Ejercicio\(\PageIndex{15}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{x+\frac{3}{5} y=-\frac{1}{5}} \\ {-\frac{1}{2} x-\frac{2}{3} y=\frac{5}{6}}\end{array}\right.\)

Contestar

(1, −2)

En el Resolviendo Sistemas de Ecuaciones por Gráfica vimos que no todos los sistemas de ecuaciones lineales tienen un solo par ordenado como solución. Cuando las dos ecuaciones eran realmente la misma línea, había infinitamente muchas soluciones. A eso lo llamamos un sistema consistente. Cuando las dos ecuaciones describieron líneas paralelas, no hubo solución. A eso lo llamamos un sistema inconsistente.

Ejercicio\(\PageIndex{16}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=3-\frac{3}{4} x}\end{array}\right.\)

Contestar

\(\begin{array} {ll} & \left\{\begin{aligned} 3 x+4 y &=12 \\ y &=3-\frac{3}{4} x \end{aligned}\right. \\\\\text{Write the second equation in standard form.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {\frac{3}{4} x+y=3}\end{array}\right.\\ \\ \text{Clear the fractions by multiplying thesecond equation by 4.} & \left\{\begin{aligned} 3 x+4 y &=12 \\ 4\left(\frac{3}{4} x+y\right) &=4(3) \end{aligned}\right. \\\\ \text{Simplify.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {3 x+4 y=12}\end{array}\right.\\\\ \text{To eliminate a variable, we multiply thesecond equation by −1.} & \left\{\begin{array}{c}{3 x+4 y=12} \\ \underline{-3 x-4 y=-12} \end{array}\right.\\ &\qquad\qquad\quad 0=0 \\ \text{Simplify and add.} \end{array}\)

Esta es una verdadera afirmación. Las ecuaciones son consistentes pero dependientes. Sus gráficas serían la misma línea. El sistema tiene infinitamente muchas soluciones.

Después de que aclaramos las fracciones en la segunda ecuación, ¿notó que las dos ecuaciones eran iguales? Eso significa que tenemos líneas coincidentes.

Ejercicio\(\PageIndex{17}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=-5+\frac{5}{3} x}\end{array}\right.\)

Contestar

infinitamente muchas soluciones

Ejercicio\(\PageIndex{18}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{x+2 y=6} \\ {y=-\frac{1}{2} x+3}\end{array}\right.\)

Contestar

infinitamente muchas soluciones

Ejercicio\(\PageIndex{19}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{-6 x+15 y=10} \\ {2 x-5 y=-5}\end{array}\right.\)

Contestar

\(\begin{array} {ll} \text{The equations are in standard form.}& \left\{\begin{aligned}-6 x+15 y &=10 \\ 2 x-5 y &=-5 \end{aligned}\right. \\\\ \text{Multiply the second equation by 3 to eliminate a variable.} & \left\{\begin{array}{l}{-6 x+15 y=10} \\ {3(2 x-5 y)=3(-5)}\end{array}\right. \\\\ \text{Simplify and add.} & \left\{\begin{aligned}{-6 x+15 y =10} \\ \underline{6 x-15 y =-15} \end{aligned}\right. \\ & \qquad \qquad \quad0\neq 5 \end{array}\)

Esta afirmación es falsa. Las ecuaciones son inconsistentes y por lo tanto sus gráficas serían líneas paralelas.

El sistema no tiene solución.

Ejercicio\(\PageIndex{20}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{-3 x+2 y=8} \\ {9 x-6 y=13}\end{array}\right.\)

Contestar

no hay solución

Ejercicio\(\PageIndex{21}\)

Resuelve el sistema por eliminación. \(\left\{\begin{array}{l}{7 x-3 y=-2} \\ {-14 x+6 y=8}\end{array}\right.\)

Contestar

no hay solución

Resolver Aplicaciones de Sistemas de Ecuaciones por Eliminación

Algunos problemas de aplicaciones se traducen directamente en ecuaciones en forma estándar, por lo que usaremos el método de eliminación para resolverlos. Como antes, utilizamos nuestra Estrategia de Resolución de Problemas para ayudarnos a mantenernos enfocados y organizados.

Ejercicio\(\PageIndex{22}\)

La suma de dos números es 39. Su diferencia es de 9. Encuentra los números.

Contestar

\(\begin{array} {ll} \textbf{Step 1. Read}\text{ the problem}& \\ \textbf{Step 2. Identify} \text{ what we are looking for.} & \text{We are looking for two numbers.} \\\textbf{Step 3. Name} \text{ what we are looking for.} & \text{Let n = the first number.} \\ & \text{ m = the second number} \\\textbf{Step 4. Translate} \text{ into a system of equations.}& \\ & \text{The sum of two numbers is 39.} \\ & n+m=39\\ & \text{Their difference is 9.} \\ & n−m=9 \\ \\ \text{The system is:} & \left\{\begin{array}{l}{n+m=39} \\ {n-m=9}\end{array}\right. \\\\ \textbf{Step 5. Solve} \text{ the system of equations. } & \\ \text{To solve the system of equations, use} \\ \text{elimination. The equations are in standard} \\ \text{form and the coefficients of m are} & \\ \text{opposites. Add.} & \left\{\begin{array}{l}{n+m=39} \\ \underline{n-m=9}\end{array}\right. \\ &\quad 2n\qquad=48 \\ \\\text{Solve for n.} & n=24 \\ \\ \text{Substitute n=24 into one of the original} &n+m=39 \\ \text{equations and solve form.} & 24+m=39 \\ & m=15 \\ \textbf{Step 6. Check}\text{ the answer.} & \text{Since 24+15=39 and 24−15=9, the answers check.}\\ \textbf{Step 7. Answer} \text{ the question.} & \text{The numbers are 24 and 15.} \end{array}\)

Ejercicio\(\PageIndex{23}\)

La suma de dos números es 42. Su diferencia es 8. Encuentra los números.

Contestar

Los números son 25 y 17.

Ejercicio\(\PageIndex{24}\)

La suma de dos números es −15. Su diferencia es −35. Encuentra los números.

Contestar

Los números son −25 y 10.

Ejercicio\(\PageIndex{25}\)

Joe se detiene en un restaurante de hamburguesas todos los días de camino al trabajo. El lunes tenía un pedido de papas fritas medianas y dos sodas pequeñas, que tenían un total de 620 calorías. El martes tuvo dos órdenes de papas fritas medianas y un refresco pequeño, para un total de 820 calorías. ¿Cuántas calorías hay en un pedido de papas fritas medianas? ¿Cuántas calorías hay en un refresco pequeño?

Contestar

Paso 1. Lee el problema.
Paso 2. Identificar lo que estamos buscando.	Estamos buscando la cantidad de calorías en un pedido de papas fritas medianas y en un refresco pequeño.
Paso 3. Nombra lo que estamos buscando.	Dejar f = el número de calorías en 1 orden de papas fritas medianas. s = el número de calorías en 1 refresco pequeño.
Paso 4. Traducir en un sistema de ecuaciones:	una papas fritas medianas y dos refrescos pequeños tenían un total de 620 calorías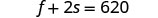
	dos papas medianas y un refresco pequeño tenían un total de 820 calorías.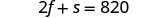
Nuestro sistema es: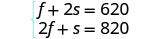
Paso 5. Resolver el sistema de ecuaciones. Para resolver el sistema de ecuaciones, utilice la eliminación. Las ecuaciones están en forma estándar. Para obtener coeficientes opuestos de f, multiplique la ecuación superior por −2.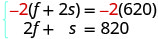
Simplificar y agregar.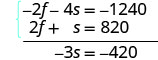
Resolver por s.
Sustituye s = 140 en una de las ecuaciones originales y luego resuelve por f.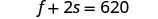
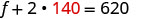
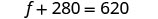
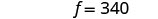
Paso 6. Consulta la respuesta.	Verificar que estos números tengan sentido en el problema y que sean soluciones a ambas ecuaciones. ¡Te dejamos esto a ti!
Paso 7. Contesta la pregunta.	El refresco pequeño tiene 140 calorías y las papas fritas tienen 340 calorías.

Ejercicio\(\PageIndex{26}\)

Malik se detiene en la tienda de abarrotes para comprar una bolsa de pañales y 2 latas de fórmula. Se gasta un total de 37 dólares. A la semana siguiente se detiene y compra 2 bolsas de pañales y 5 latas de fórmula por un total de 87 dólares. ¿Cuánto cuesta una bolsa de pañales? ¿Cuánto cuesta una lata de fórmula?

Contestar

La bolsa de pañales cuesta $11 y la lata de fórmula cuesta $13.

Ejercicio\(\PageIndex{27}\)

Para obtener su ingesta diaria de fruta para el día, Sasha se come un plátano y 8 fresas el miércoles por un recuento calórico de 145. El miércoles siguiente, come dos plátanos y 5 fresas para un total de 235 calorías para la fruta. ¿Cuántas calorías hay en un plátano? ¿Cuántas calorías hay en una fresa?

Contestar

Hay 105 calorías en un plátano y 5 calorías en una fresa.

Elija el método más conveniente para resolver un sistema de ecuaciones lineales

Cuando tendrás que resolver un sistema de ecuaciones lineales en una clase de matemáticas posterior, normalmente no se te dirá qué método usar. Tendrás que tomar esa decisión tú mismo. Así que querrás elegir el método que sea más fácil de hacer y minimice tus posibilidades de cometer errores.

Ejercicio\(\PageIndex{28}\)

Para cada sistema de ecuaciones lineales decidir si sería más conveniente resolverlo por sustitución o eliminación. Explica tu respuesta.

1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

Contestar

1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)

Dado que ambas ecuaciones están en forma estándar, usar la eliminación será lo más conveniente.

2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

Dado que una ecuación ya está resuelta para y, el uso de la sustitución será lo más conveniente.

Ejercicio\(\PageIndex{29}\)

Para cada sistema de ecuaciones lineales, decidir si sería más conveniente resolverlo por sustitución o eliminación. Explica tu respuesta.

1. \(\left\{\begin{array}{l}{4 x-5 y=-32} \\ {3 x+2 y=-1}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{x=2 y-1} \\ {3 x-5 y=-7}\end{array}\right.\)

Contestar

1. Dado que ambas ecuaciones están en forma estándar, usar la eliminación será lo más conveniente.
2. Dado que una ecuación ya está resuelta para xx, el uso de la sustitución será lo más conveniente.

Ejercicio\(\PageIndex{30}\)

Para cada sistema de ecuaciones lineales, decidir si sería más conveniente resolverlo por sustitución o eliminación. Explica tu respuesta.

1. \(\left\{\begin{array}{l}{y=2 x-1} \\ {3 x-4 y=-6}\end{array}\right.\)
2. \(\left\{\begin{array}{l}{6 x-2 y=12} \\ {3 x+7 y=-13}\end{array}\right.\)

Contestar

1. Dado que una ecuación ya está resuelta para yy, usar la sustitución será lo más conveniente;
2. Dado que ambas ecuaciones están en forma estándar, usar la eliminación será lo más conveniente.

Nota

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con sistemas de resolución de ecuaciones lineales por eliminación.

• Sistemas instruccionales de video resolución de ecuaciones por eliminación
• Resolución de video instruccional por eliminación
• Sistemas de resolución de video instructivos por eliminación

Conceptos clave

• Resolver un sistema de ecuaciones por eliminación
  1. Escribe ambas ecuaciones en forma estándar. Si alguno de los coeficientes son fracciones, límpielos.
  2. Hacer los coeficientes de una variable opuestos.
     • Decide qué variable vas a eliminar.
     • Multiplique una o ambas ecuaciones para que los coeficientes de esa variable sean opuestos.
  3. Agregue las ecuaciones resultantes del Paso 2 para eliminar una variable.
  4. Resolver para la variable restante.
  5. Sustituir la solución del Paso 4 por una de las ecuaciones originales. Entonces resuelve para la otra variable.
  6. Escribe la solución como un par ordenado.
  7. Comprobar que el par ordenado es una solución a ambas ecuaciones originales.