7.3E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 110199

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Reconocer una estrategia preliminar para factorizar polinomios por completo

En los siguientes ejercicios, identificar el mejor método a utilizar para factorizar cada polinomio.

Ejercicio 1

$10q^2+50$
$a^2−5a−14$
$uv+2u+3v+6$

Responder

factor el GCF, binomio
Deshacer FOIL
factor por agrupación

Ejercicio 2

$n^2+10n+24$
$8u^2+16$
$pq+5p+2q+10$

Ejercicio 3

$x^2+4x−21$
$ab+10b+4a+40$
$6c^2+24$

Responder

deshacer FOIL
factor por agrupación
factor el GCF, binomio

Ejercicio 4

$20x^2+100$
$uv+6u+4v+24$
$y^2−8y+15$

Trinomios factoriales de la forma$ax^2+bx+c$ con un GCF

En los siguientes ejercicios, factorizar completamente.

Ejercicio 5

$5x^2+35x+30$

Contestar: $5(x+1)(x+6)$

Ejercicio 6

$12s^2+24s+12$

Ejercicio 7

$2z^2−2z−24$

Contestar: $2(z−4)(z+3)$

Ejercicio 8

$3u^2−12u−36$

Ejercicio 9

$7v^2−63v+56$

Contestar: $7(v−1)(v−8)$

Ejercicio 10

$5w^2−30w+45$

Ejercicio 11

$p^3−8p^2−20p$

Contestar: $p(p−10)(p+2)$

Ejercicio 12

$q^3−5q^2−24q$

Ejercicio 13

$3m^3−21m^2+30m$

Contestar: $3m(m−5)(m−2)$

Ejercicio 14

$11n^3−55n^2+44n$

Ejercicio 15

$5x^4+10x^3−75x^2$

Contestar: $5x^{2}(x−3)(x+5)$

Ejercicio 16

$6y^4+12y^3−48y^2$

Trinomios factoriales usando prueba y error

En los siguientes ejercicios, factor.

Ejercicio 17

$2t^2+7t+5$

Contestar: $(2t+5)(t+1)$

Ejercicio 18

$5y^2+16y+11$

Ejercicio 19

$11x^2+34x+3$

Contestar: $(11x+1)(x+3)$

Ejercicio 20

$7b^2+50b+7$

Ejercicio 21

$4w^2−5w+1$

Contestar: $(4w−1)(w−1)$

Ejercicio 22

$5x^2−17x+6$

Ejercicio 23

$6p^2−19p+10$

Contestar: $(3p−2)(2p−5)$

Ejercicio 24

$21m^2−29m+10$

Ejercicio 25

$4q^2−7q−2$

Contestar: $(4q+1)(q−2)$

Ejercicio 26

$10y^2−53y−11$

Ejercicio 27

$4p^2+17p−15$

Contestar: $(4p−3)(p+5)$

Ejercicio 28

$6u^2+5u−14$

Ejercicio 29

$16x^2−32x+16$

Contestar: $16(x−1)(x−1)$

Ejercicio 30

$81a^2+153a−18$

Ejercicio 31

$30q^3+140q^2+80q$

Contestar: $10q(3q+2)(q+4)$

Ejercicio 32

$5y^3+30y^2−35y$

Trinomios factoriales usando el Método 'ac'

En los siguientes ejercicios, factor.

Ejercicio 33

$5n^2+21n+4$

Contestar: $(5n+1)(n+4)$

Ejercicio 34

$8w^2+25w+3$

Ejercicio 35

$9z^2+15z+4$

Contestar: $(3z+1)(3z+4)$

Ejercicio 36

$3m^2+26m+48$

Ejercicio 37

$4k^2−16k+15$

Contestar: $(2k−3)(2k−5)$

Ejercicio 38

$4q^2−9q+5$

Ejercicio 39

$5s^2−9s+4$

Contestar: $(5s−4)(s−1)$

Ejercicio 40

$4r^2−20r+25$

Ejercicio 41

$6y^2+y−15$

Contestar: $(3y+5)(2y−3)$

Ejercicio 42

$6p^2+p−22$

Ejercicio 43

$2n^2−27n−45$

Contestar: $(2n+3)(n−15)$

Ejercicio 44

$12z^2−41z−11$

Ejercicio 45

$3x^2+5x+4$

Contestar: prime

Ejercicio 46

$4y^2+15y+6$

Ejercicio 47

$60y^2+290y−50$

Contestar: $10(6y−1)(y+5)$

Ejercicio 48

$6u^2−46u−16$

Ejercicio 49

$48z^3−102z^2−45z$

Contestar: $3z(8z+3)(2z−5)$

Ejercicio 50

$90n^3+42n^2−216n$

Ejercicio 51

$16s^2+40s+24$

Contestar: $8(2s+3)(s+1)$

Ejercicio 52

$24p^2+160p+96$

Ejercicio 53

$48y^2+12y−36$

Contestar: $12(4y−3)(y+1)$

Ejercicio 54

$30x^2+105x−60$

Práctica Mixta

En los siguientes ejercicios, factor.

Ejercicio 55

$12y^2−29y+14$

Contestar: $(4y−7)(3y−2)$

Ejercicio 56

$12x^2+36y−24z$

Ejercicio 57

$a^2−a−20$

Contestar: $(a−5)(a+4)$

Ejercicio 58

$m^2−m−12$

Ejercicio 59

$6n^2+5n−4$

Contestar: $(2n−1)(3n+4)$

Ejercicio 60

$12y^2−37y+21$

Ejercicio 61

$2p^2+4p+3$

Contestar: prime

Ejercicio 62

$3q^2+6q+2$

Ejercicio 63

$13z^2+39z−26$

Contestar: $13(z^2+3z−2)$

Ejercicio 64

$5r^2+25r+30$

Ejercicio 65

$x^2+3x−28$

Contestar: $(x+7)(x−4)$

Ejercicio 66

$6u^2+7u−5$

Ejercicio 67

$3p^2+21p$

Contestar: $3p(p+7)$

Ejercicio 68

$7x^2−21x$

Ejercicio 69

$6r^2+30r+36$

Contestar: $6(r+2)(r+3)$

Ejercicio 70

$18m^2+15m+3$

Ejercicio 71

$24n^2+20n+4$

Contestar: $4(2n+1)(3n+1)$

Ejercicio 72

$4a^2+5a+2$

Ejercicio 73

$x^2+2x−24$

Contestar: $(x+6)(x−4)$

Ejercicio 74

$2b^2−7b+4$

Matemáticas cotidianas

Ejercicio 75

Altura de un cohete de juguete La altura de un cohete de juguete lanzado con una velocidad inicial de$80$ pies por segundo desde el balcón de un edificio de departamentos está relacionada con el número de segundos$t$,, ya que es lanzado por el trinomio$−16t^2+80t+96$. Factorar este trinomio.

Contestar: $−16(t−6)(t+1)$

Ejercicio 76

Altura de una pelota de playa La altura de una pelota de playa arrojada con una velocidad inicial de$12$ pies por segundo desde una altura de$4$ pies está relacionada con el número de segundos$t$, ya que es arrojado por el trinomio$−16t^2+12t+4$. Factorar este trinomio.

Ejercicios de escritura

Ejercicio 77

Enumere, en orden, todos los pasos que realice al usar el método “$ac$” para factorizar un trinomio de la forma$ax^2+bx+c$.

Contestar: Las respuestas pueden variar.

Ejercicio 78

¿Cómo es el método “$ac$” similar al método “undo FOIL”? ¿En qué se diferencia?

Ejercicio 79

¿Cuáles son las preguntas, en orden, que te haces a medida que empiezas a factorizar un polinomio? ¿Qué necesitas hacer como resultado de la respuesta a cada pregunta?

Contestar: Las respuestas pueden variar.

Ejercicio 80

En su papel dibuja el gráfico que resume la estrategia de factorización. Intenta hacerlo sin mirar el libro. Cuando hayas terminado, mira hacia atrás en el libro para terminarlo o verifícalo.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

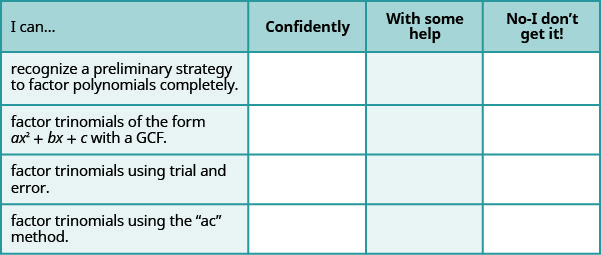
$Esta tabla tiene las siguientes declaraciones todas para ir precedidas de “Yo puedo...”. La primera fila es “reconocer una estrategia preliminar para factorizar polinomios por completo”. La segunda fila es “trinomios factoriales de la forma a x ^ 2 + b x + c con un GCF”. La tercera fila es “trinomios factoriales usando ensayo y error”. Y la cuarta fila es “trinomios factoriales usando el método “ac””. En las columnas al lado de estas declaraciones están los encabezados, “confiadamente”, “con alguna ayuda”, y “¡No-no lo consigo!”.$

b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?