7.3: Trinomios cuadráticos factoriales con coeficiente principal distinto de 1
- Page ID
- 110195
Al final de esta sección, podrás:
- Reconocer una estrategia preliminar para factorizar polinomios por completo
- Trinomios factoriales de la forma\(ax^{2}+bx+c\) con un GCF
- Trinomios factoriales usando ensayo y error
- Trinomios factoriales usando el método 'ac'
Antes de comenzar, toma este cuestionario de preparación.
- Encuentra el GCF de 45\(p^{2}\) y 30\(p^{6}\)
Si te perdiste este problema, revisa Ejercicio 7.1.4. - Multiplicar\((3 y+4)(2 y+5)\)
Si te perdiste este problema, revisa Ejercicio 6.3.37. - Combina términos similares\(12 x^{2}+3 x+5 x+9\)
Si te perdiste este problema, revisa Ejercicio 1.3.37.
Reconocer una estrategia preliminar para el factoraje
Resumamos dónde estamos hasta el momento con factorización de polinomios. En las dos primeras secciones de este capítulo, se utilizaron tres métodos de factorización: factorizar el GCF, factorizar por agrupación y factorizar un trinomio por “deshacer” FOIL. Seguirán más métodos a medida que continúe en este capítulo, así como posteriormente en sus estudios de álgebra.
¿Cómo sabrás cuándo usar cada método de factoring? A medida que aprendes más métodos de factoraje, ¿cómo sabrás cuándo aplicar cada método y no confundirlos? Ayudará a organizar los métodos de factoring en una estrategia que pueda guiarlo para usar el método correcto.
A medida que empiezas a factorizar un polinomio, siempre pregunta primero: “¿Existe un mayor factor común?” Si la hay, factorizarlo primero.
Lo siguiente a considerar es el tipo de polinomio. ¿Cuántos términos tiene? ¿Es un binomio? ¿Un trinomio? ¿O tiene más de tres términos?
- Si se trata de un trinomio donde el coeficiente principal es uno,\(x^{2}+b x+c\), utilice el método “undo FOIL”.
- Si tiene más de tres términos, pruebe el método de agrupación. Este es el único método a utilizar para polinomios de más de tres términos.
Algunos polinomios no pueden ser factorizados. Se les llama “prime”. A continuación resumimos los métodos que tenemos hasta el momento.
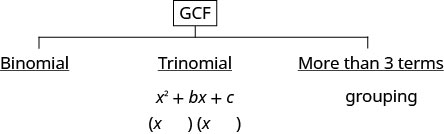
- ¿Hay un factor común más grande?
- Facturarlo.
- ¿Es el polinomio un binomio, trinomio, o hay más de tres términos?
- Si es un binomio, en estos momentos no tenemos ningún método para factorizarlo.
- Si es un trinomio de la forma\(x^{2}+b x+c\): Deshacer FOIL\((x\qquad)(x\qquad)\)
- Si tiene más de tres términos: Usa el método de agrupación.
- Verificar multiplicando los factores.
Utilizar la estrategia preliminar para factorizar completamente un polinomio. Un polinomio se factoriza completamente si, aparte de los monomios, todos sus factores son primos.
Identificar el mejor método a utilizar para factorizar cada polinomio.
- \(6 y^{2}-72\)
- \(r^{2}-10 r-24\)
- \(p^{2}+5 p+p q+5 q\)
- Responder a
-
\[\begin{array}{ll} &6 y^{2}-72\\ \text { Is there a greatest common factor? } & \text {Yes, 6. } \\ \text { Factor out the } 6 &6\left(y^{2}-12\right) \\ \text { Is it a binomial, trinomial, or are there } & \text {Binomial, we have no method to factor } \\ \text { more than } 3 \text { terms? } & \text {binomials yet. } \end{array} \nonumber\]
- Respuesta b
-
\[\begin{array}{ll} &r^{2}-10 r-24\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {Trinomial, with leading coefficient } 1, \text { so } \\ \text { more than three terms? }& \text {"undo" FOIL. }\end{array} \nonumber\]
- Respuesta c
-
\[\begin{array}{ll} &p^{2}+5 p+p q+5 q\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {More than three terms, so factor using }\\ \text { more than three terms? }& \text {grouping. }\end{array} \nonumber\]
Identificar el mejor método a utilizar para factorizar cada polinomio:
- \(4 y^{2}+32\)
- \(y^{2}+10 y+21\)
- \(y z+2 y+3 z+6\)
- Responder a
-
ningún método
- Respuesta b
-
deshacer usando FOIL
- Respuesta c
-
factor con agrupación
Identificar el mejor método a utilizar para factorizar cada polinomio:
- \(a b+a+4 b+4\)
- \(3 k^{2}+15\)
- \(p^{2}+9 p+8\)
- Responder a
-
factor usando agrupación
- Respuesta b
-
ningún método
- Respuesta c
-
deshacer usando FOIL
Trinomios factoriales de la forma ax 2 + bx + c con un GCF
Ahora que hemos organizado lo que hemos cubierto hasta ahora, estamos listos para factorizar trinomios cuyo coeficiente principal no es 1, trinomios de la forma\(a x^{2}+b x+c\). ¡Recuerda siempre verificar primero un GCF! En ocasiones, después de factorizar el GCF, el coeficiente principal del trinomio se convierte en 1 y puedes factorizarlo por los métodos de la última sección. Hagamos algunos ejemplos para ver cómo funciona esto. Cuidado con las señales en los siguientes dos ejemplos.
Factor completamente:\(2 n^{2}-8 n-42\).
- Contestar
-
Utilizar la estrategia preliminar.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&2 n^{2}-8 n-42\\ \text { Yes, GCF }=2 . \text { Factor it out. }& 2\left(n^{2}-4 n-21\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 2(n\qquad )(n\qquad) \\ \text { Use } 3 \text { and }-7 \text { as the last terms of the binomials. } & 2(n+3)(n-7) \end{array}\)
Factores de −21 Suma de factores 1, −21 1+ (−21) =−20 3, −7 3+ (−7) =−4* \(\begin{array}{l}{\text {Check. }} \\ {2(n+3)(n-7)} \\ {2\left(n^{2}-7 n+3 n-21\right)} \\ {2\left(n^{2}-4 n-21\right)} \\ {2 n^{2}-8 n-42 }\checkmark \end{array}\)
Factor completamente:\(4 m^{2}-4 m-8\)
- Contestar
-
4\((m+1)(m-2)\)
Factor completamente:\(5 k^{2}-15 k-50\)
- Contestar
-
5\((k+2)(k-5)\)
Factor completamente:\(4 y^{2}-36 y+56\)
- Contestar
-
Utilizar la estrategia preliminar.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 y^{2}-36 y+56\\ \text { Yes, GCF }=4 . \text { Factor it out. }&4\left(y^{2}-9 y+14\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 4(y\qquad )(y\qquad) \\\text { Use a table like the one below to find two numbers that multiply to }&\\ 14 \text { and add to }-9\\ \text { Both factors of } 14 \text { must be negative. } & 4(y-2)(y-7) \end{array}\)Factores de 14 Suma de factores −1, −14 −1+ (−14) =−15 −2, −7 −2+ (−7) =−9* \(\begin{array}{l}{\text { Check. }} \\ {4(y-2)(y-7)} \\ {4\left(y^{2}-7 y-2 y+14\right)} \\ {4\left(y^{2}-9 y+14\right)} \\ {4 y^{2}-36 y+42 } \checkmark \end{array}\)
Factor completamente:\(3 r^{2}-9 r+6\)
- Contestar
-
3\((r-1)(r-2)\)
Factor completamente:\(2 t^{2}-10 t+12\)
- Contestar
-
2\((t-2)(t-3)\)
En el siguiente ejemplo el GCF incluirá una variable.
Factor completamente:\(4 u^{3}+16 u^{2}-20 u\)
- Contestar
-
Utilizar la estrategia preliminar.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 u^{3}+16 u^{2}-20 u\\ \text { Yes, GCF }=4 u . \text { Factor it. }&4 u\left(u^{2}+4 u-5\right) \\\text { Binomial, trinomial, or more than three terms? }&\\ \text { more than three terms? }& \\ \text { It is a trinomial. So "undo FOIL." } & 4u(u\qquad )(u\qquad) \\\text { Use a table like the table below to find two numbers that }&4 u(u-1)(u+5)\\ \text { multiply to }-5 \text { and add to } 4\end{array}\)Factores de −5 Suma de factores −1,5 −1+5=4* 1, −5 1+ (−5) =−4 Cheque.
\(\begin{array}{l}{4 u(u-1)(u+5)} \\ {4 u\left(u^{2}+5 u-u-5\right)} \\ {4 u\left(u^{2}+4 u-5\right)} \\ {4 u^{3}+16 u^{2}-20 u }\checkmark \end{array}\)
Factor completamente:\(5 x^{3}+15 x^{2}-20 x\)
- Contestar
-
5\(x(x-1)(x+4)\)
Factor completamente:\(6 y^{3}+18 y^{2}-60 y\)
- Contestar
-
6\(y(y-2)(y+5)\)
Trinomios factoriales usando Prueba y Error
¿Qué sucede cuando el coeficiente principal no es 1 y no hay GCF? Existen varios métodos que se pueden utilizar para factorizar estos trinomios. Primero usaremos el método de Prueba y Error.
Vamos a factorizar el trinomio\(3 x^{2}+5 x+2\)
De nuestro trabajo anterior esperamos que esto se factorizará en dos binomios.
\[\begin{array}{c}{3 x^{2}+5 x+2} \\ {( \qquad)( \qquad)}\end{array}\]
Sabemos que los primeros términos de los factores binomiales se multiplicarán para darnos 3\(x^{2}\). Los únicos factores de 3\(x^{2}\) son\(1 x, 3 x\). Podemos colocarlos en los binomios.
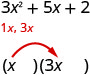
Cheque. ¿Lo hace\(1 x \cdot 3 x=3 x^{2}\)?
Sabemos que los últimos términos de los binomios se multiplicarán a 2. Dado que este trinomio tiene todos los términos positivos, solo necesitamos considerar factores positivos. Los únicos factores de 2 son 1 y 2. Pero ahora tenemos dos casos a considerar ya que marcará la diferencia si escribimos 1, 2, o 2, 1.

¿Qué factores son correctos? Para decidir eso, multiplicamos los términos interno y externo.
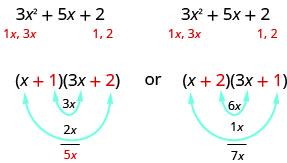
Dado que el término medio del trinomio es 5 x, los factores en el primer caso funcionarán. Vamos a FOIL para verificar.
\[\begin{array}{l}{(x+1)(3 x+2)} \\ {3 x^{2}+2 x+3 x+2} \\ {3 x^{2}+5 x+2}\checkmark \end{array}\]
Nuestro resultado del factoring es:
\[\begin{array}{l}{3 x^{2}+5 x+2} \\ {(x+1)(3 x+2)}\end{array}\]
Factor completamente:\(3 y^{2}+22 y+7\)
- Contestar
-





Factor completamente:\(2 a^{2}+5 a+3\)
- Contestar
-
\((a+1)(2 a+3)\)
Factor completamente:\(4 b^{2}+5 b+1\)
- Contestar
-
\((b+1)(4 b+1)\)
- Escribir el trinomio en orden descendente de grados.
- Encuentra todos los pares de factores del primer término.
- Encuentra todos los pares de factores del tercer término.
- Pruebe todas las combinaciones posibles de los factores hasta encontrar el producto correcto.
- Verificar multiplicando.
Cuando el término medio es negativo y el último término es positivo, los signos en los binomios deben ser ambos negativos.
Factor completamente:\(6 b^{2}-13 b+5\)
- Contestar
-
Considera todas las combinaciones de factores.El trinomio ya está en orden descendente. 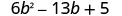
Encuentra los factores del primer término. 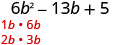
Encuentra los factores del último término. Considera las señales. Desde el último término, 5 es positivo sus factores deben ser ambos positivos o ambos ser negativos. El coeficiente del término medio es negativo, por lo que utilizamos los factores negativos. 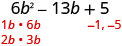
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 b-1)(3 b-5)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 v}\checkmark \end{array}\end{array}\)\(6 b^{2}-13 b+5\) Posibles factores Producto \ (6 b^ {2} -13 b+5\) Factores posibles” data-valign="top” class="lt-math-15168"> (b−1) (6b−5) \ (6 b^ {2} -13 b+5\) Producto” data-valign="top” class="lt-math-15168">\(6 b^{2}-11 b+5\) \ (6 b^ {2} -13 b+5\) Factores posibles” data-valign="top” class="lt-math-15168"> (b−5) (6b−1) \ (6 b^ {2} -13 b+5\) Producto” data-valign="top” class="lt-math-15168">\(6 b^{2}-31 b+5\) \ (6 b^ {2} -13 b+5\) Factores posibles” data-valign="top” class="lt-math-15168"> (2b−1) (3b−5) \ (6 b^ {2} -13 b+5\) Producto” data-valign="top” class="lt-math-15168">\(6 b^{2}-13 b+5\) * \ (6 b^ {2} -13 b+5\) Factores posibles” data-valign="top” class="lt-math-15168"> (2b−5) (3b−1) \ (6 b^ {2} -13 b+5\) Producto” data-valign="top” class="lt-math-15168">\(6 b^{2}-17 b+5\)
Factor completamente:\(8 x^{2}-14 x+3\)
- Contestar
-
\((2 x-3)(4 x-1)\)
Factor completamente:\(10 y^{2}-37 y+7\)
- Contestar
-
\((2 y-7)(5 y-1)\)
Cuando factorizamos una expresión, siempre buscamos primero un factor común más grande. Si la expresión no tiene un mayor factor común, tampoco puede haber uno en sus factores. Esto puede ayudarnos a eliminar algunas de las posibles combinaciones de factores.
Factor completamente:\(14 x^{2}-47 x-7\)
- Contestar
-
Considera todas las combinaciones de factores. Utilizamos cada par de los factores de 14\(x^{2}\) con cada par de factores de −7.El trinomio ya está en orden descendente. 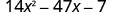
Encuentra los factores del primer término. 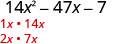
Encuentra los factores del último término. Considera las señales. Al ser negativo, un factor debe ser positivo y otro negativo. 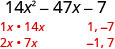
Factores de\(14x^2\) Empareja con Factores de −7 \ (14x^2\)” data-valign="top” class="lt-math-15168">\(x, 14 x\) 11, −7
−7, 11
(orden inverso)\ (14x^2\)” data-valign="top” class="lt-math-15168">\(x, 14 x\) −1, 77
77, −1
(orden inverso)\ (14x^2\)” data-valign="top” class="lt-math-15168">\(2x,7x\) 11, −7
−7, 11
(orden inverso)\ (14x^2\)” data-valign="top” class="lt-math-15168">\(2x,7x\) −1, 77
77, −1
(orden inverso)Estos emparejamientos conducen a las siguientes ocho combinaciones.
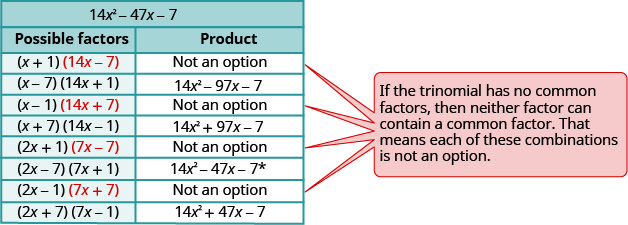
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 x-7)(7 x+1)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 }\checkmark \end{array}\end{array}\)
Factor completamente:\(8 a^{2}-3 a-5\)
- Contestar
-
\((a-1)(8 a+5)\)
Factor completamente:\(6 b^{2}-b-15\)
- Contestar
-
\((2 b+3)(3 b-5)\)
Factor completamente:\(18 n^{2}-37 n+15\)
- Contestar
-
El trinomio ya está en orden descendente. \(18 n^{2}-37 n+15\) Encuentra los factores del primer término. 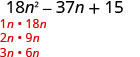
Encuentra los factores del último término. Considera las señales. Dado que 15 es positivo y el coeficiente del término medio es negativo, utilizamos los factores negativos. 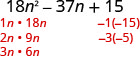
Considera todas las combinaciones de factores.

\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 n-3)(9 n-5)\\\\\text {Check by multiplying. } \\\\ \begin{array}{l}{(2 n-3)(9 n-5)} \\ {18 n^{2}-10 n-27 n+15} \\ {18 n^{2}-37 n+15 } \checkmark\end{array} \end{array}\)
Factor completamente:\(18 x^{2}-3 x-10\)
- Contestar
-
\((3 x+2)(6 x-5)\)
Factor completamente:\(30 y^{2}-53 y-21\)
- Contestar
-
\((3 y+1)(10 y-21)\)
No olvides buscar primero un GCF.
Factor completamente:\(10 y^{4}+55 y^{3}+60 y^{2}\)
- Contestar
-
\(10 y^{4}+55 y^{3}+60 y^{2}\) Observe el mayor factor común, y factorizarlo primero. 5\(y^{2}\left(2 y^{2}+11 y+12\right)\) Factorial el trinomio. 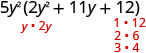
Considera todas las combinaciones.
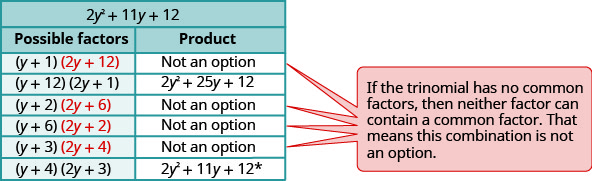
\(\begin{array}{ll}\text{The correct factors are those whose product} &5 y^{2}(y+4)(2 y+3) \\ \text{is the original trinomial. Remember to include} & \\\text {the factor } 5 y^{2}\\\text {Check by multiplying. } \\\\ \begin{array}{l}{5 y^{2}(y+4)(2 y+3)} \\ {5 y^{2}\left(2 y^{2}+8 y+3 y+12\right)} \\ {10 y^{4}+55 y^{3}+60 y^{2}}\checkmark\end{array} \end{array}\)
Factor completamente:\(15 n^{3}-85 n^{2}+100 n\)
- Contestar
-
5\(n(n-4)(3 n-5)\)
Factor completamente:\(56 q^{3}+320 q^{2}-96 q\)
- Contestar
-
8\(q(q+6)(7 q-2)\)
Trinomios factoriales usando el Método “ac”
Otra forma de factorizar trinomios de la forma\(ax^2+bx+c\) es el método “ac”. (El método “ac” a veces se llama método de agrupación.) El método “ac” es en realidad una extensión de los métodos que utilizó en la última sección para factorizar trinomios con coeficiente inicial uno. Este método es muy estructurado (eso es paso a paso), ¡y siempre funciona!
Factor:\(6 x^{2}+7 x+2\)
- Contestar
-


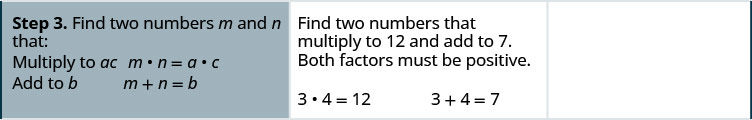



Factor:\(6 x^{2}+13 x+2\)
- Contestar
-
\((x+2)(6 x+1)\)
Factor:\(4 y^{2}+8 y+3\)
- Contestar
-
\((2 y+1)(2 y+3)\)
- Facturar cualquier GCF.
- Encuentra el producto ac.
- Encuentra dos números m y n que:
\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\) - Dividir el término medio usando m y n:
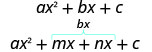
- Factor por agrupación.
- Verificar multiplicando los factores.
Cuando el tercer término del trinomio sea negativo, los factores del tercer término tendrán signos opuestos.
Factor:\(8 u^{2}-17 u-21\)
- Contestar
-
¿Hay un factor común más grande? No. 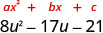
Encuentra\(a\cdot c\) \(a\cdot c\) 8 (−21) −168 Encuentra dos números que se multiplican a −168 y se suman a −17. El factor mayor debe ser negativo.
Factores de −168 Suma de factores 1, −168 1+ (−168) =−167 2, −84 2+ (−84) =−82 3, −56 3+ (−56) =−53 4, −42 4+ (−42) =−38 6, −28 6+ (−28) =−22 7, −24 7+ (−24) =−17* 8, −21 8+ (−21) =−13 \(\begin{array}{lc}\text { Split the middle term using } 7 u \text { and }-24 u &8 u^{2}-17 u-21 \\ & \qquad\space \swarrow\searrow \\ & \underbrace{8 u^{2}+7 u} \underbrace{-24 u-21} \\ \text { Factor by grouping. } & u(8 u+7)-3(8 u+7) \\ & (8 u+7)(u-3) \\ \text { Check by multiplying. } & \begin{array}{l}{(8 u+7)(u-3)} \\ {8 u^{2}-24 u+7 u-21} \\ {8 u^{2}-17 u-21} \checkmark \end{array} \end{array}\)
Factor:\(20 h^{2}+13 h-15\)
- Contestar
-
\((4 h-5)(5 h+3)\)
Factor:\(6 g^{2}+19 g-20\)
- Contestar
-
\((q+4)(6 q-5)\)
Factor:\(2 x^{2}+6 x+5\)
- Contestar
-
¿Hay un factor común más grande? No. 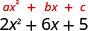
Encuentra ac ac 2 (5) 10 Encuentra dos números que se multiplican a 10 y se suman a 6.
Factores de 10 Suma de factores 1,10 1+10=11 2, 5 2+5=7 No hay factores que se multipliquen a 10 y sumen a 6. El polinomio es primo.
Factor:\(10 t^{2}+19 t-15\)
- Contestar
-
\((2 t+5)(5 t-3)\)
Factor:\(3 u^{2}+8 u+5\)
- Contestar
-
\((u+1)(3 u+5)\)
¡No olvides buscar un factor común!
Factor:\(10 y^{2}-55 y+70\)
- Contestar
-
¿Hay un factor común más grande? Sí. El GCF es 5. 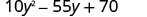
Factorizarlo. ¡Tenga cuidado de mantener el factor de 5 en todo el camino a través de la solución! 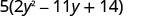
El trinomio dentro de los paréntesis tiene un coeficiente principal que no es 1. 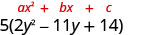
Factorial el trinomio. 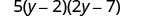
Verifique multiplicando los tres factores. 5\(\left(2 y^{2}-2 y-4 y+14\right)\) 5\(\left(2 y^{2}-11 y+14\right)\) \(10 y^{2}-55 y+70\)✓
Factor:\(16 x^{2}-32 x+12\)
- Contestar
-
4\((2 x-3)(2 x-1)\)
Factor:\(18 w^{2}-39 w+18\)
- Contestar
-
3\((3 w-2)(2 w-3)\)
Ahora podemos actualizar la Estrategia Preliminar de Factoring, tal\(\PageIndex{1}\) y como se muestra en Figura y se detalla en Elija una estrategia para factorizar polinomios completamente (actualizado), para incluir trinomios de la forma\(a x^{2}+b x+c\). Recuerden, algunos polinomios son primos y por lo tanto no pueden ser factorizados.

- ¿Hay un factor común más grande?
- Factorizarlo.
- ¿Es el polinomio un binomio, trinomio, o hay más de tres términos?
- Si es un binomio, en estos momentos no tenemos ningún método para factorizarlo.
- Si es un trinomio de la forma\(x^{2}+b x+c\)
Deshacer FOIL\\((x\qquad)(x\qquad)\). - Si se trata de un trinomio de la forma\(a x^{2}+b x+c\)
Use Prueba y Error o el método “ac”. - Si tiene más de tres términos
Usa el método de agrupación.
- Verificar multiplicando los factores.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con trinomios de factorización del formulario\(a x^{2}+b x+c\)
Conceptos clave
- Trinomios factoriales de la Forma\(a x^{2}+b x+c\) usando Prueba y Error: Ver Ejemplo.
- Escribir el trinomio en orden descendente de grados.
- Encuentra todos los pares de factores del primer término.
- Encuentra todos los pares de factores del tercer término.
- Pruebe todas las combinaciones posibles de los factores hasta encontrar el producto correcto.
- Verificar multiplicando.
- Trinomios Factoriales de la Forma\(a x^{2}+b x+c\) Usando el Método “ac”: Ver Ejemplo.
- Facturar cualquier GCF.
- Encuentra el producto ac.
- Encuentra dos números m y n que:\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
- Dividir el término medio usando m y n:
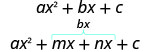
- Factor por agrupación.
- Verificar multiplicando los factores.
- Elige una estrategia para factorizar polinomios completamente (actualizado):
- ¿Hay un factor común más grande? Factorizarlo.
- ¿Es el polinomio un binomio, trinomio, o hay más de tres términos?
Si es un binomio, en estos momentos no tenemos ningún método para factorizarlo.
Si se trata de un trinomio de la forma\(x^2+bx+c\)
Deshacer FOIL\((x\qquad)(x\qquad)\).
Si se trata de un trinomio de la forma\(ax^2+bx+c\)
Use Prueba y Error o el método “ac”.
Si tiene más de tres términos
Usa el método de agrupación. - Verificar multiplicando los factores.
Glosario
- polinomios primos
- Los polinomios que no se pueden factorizar son polinomios primos.


