7.4E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 110207

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Trinomios cuadrados perfectos de factor

En los siguientes ejercicios, factor.

Ejercicio 1

$16y^2+24y+9$

Contestar: $(4y+3)^2$

Ejercicio 2

$25v^2+20v+4$

Ejercicio 3

$36s^2+84s+49$

Contestar: $(6s+7)^2$

Ejercicio 4

$49s^2+154s+121$

Ejercicio 5

$100x^2−20x+1$

Contestar: $(10x−1)^2$

Ejercicio 6

$64z^2−16z+1$

Ejercicio 7

$25n^2−120n+144$

Contestar: $(5n−12)^2$

Ejercicio 8

$4p^2−52p+169$

Ejercicio 9

$49x^2−28xy+4y^2$

Contestar: $(7x−2y)^2$

Ejercicio 10

$25r^2−60rs+36s^2$

Ejercicio 11

$25n^2+25n+4$

Contestar: $(5n+4)(5n+1)$

Ejercicio 12

$100y^2−20y+1$

Ejercicio 13

$64m^2−16m+1$

Contestar: $(8m-1)^2$

Ejercicio 14

$100x^2−25x+1$

Ejercicio 15

$10k^2+80k+160$

Contestar: $10(k+4)^2$

Ejercicio 16

$64x^2−96x+36$

Ejercicio 17

$75u^3−30u^{2}v+3uv^2$

Contestar: $3u(5u−v)^2$

Ejercicio 18

$90p^3+300p^{2}q+250pq^2$

Diferencias de factores de cuadrados

En los siguientes ejercicios, factor.

Ejercicio 19

$x^2−16$

Contestar: $(x−4)(x+4)$

Ejercicio 20

$n^2−9$

Ejercicio 21

$25v^2−1$

Contestar: $(5v−1)(5v+1)$

Ejercicio 22

$169q^2−1$

Ejercicio 23

$121x^2−144y^2$

Contestar: $(11x−12y)(11x+12y)$

Ejercicio 24

$49x^2−81y^2$

Ejercicio 25

$169c^2−36d^2$

Contestar: $(13c−6d)(13c+6d)$

Ejercicio 26

$36p^2−49q^2$

Ejercicio 27

$4−49x^2$

Contestar: $(2−7x)(2+7x)$

Ejercicio 28

$121−25s^2$

Ejercicio 29

$16z^4−1$

Contestar: $(2z−1)(2z+1)(4z^2+1)$

Ejercicio 30

$m^4−n^4$

Ejercicio 31

$5q^2−45$

Contestar: $5(q−3)(q+3)$

Ejercicio 32

$98r^3−72r$

Ejercicio 33

$24p^2+54$

Contestar: $6(4p^2+9)$

Ejercicio 34

$20b^2+140$

Sumas de factores y diferencias de cubos

En los siguientes ejercicios, factor.

Ejercicio 35

$x^3+125$

Contestar: $(x+5)(x^2−5x+25)$

Ejercicio 36

$n^3+512$

Ejercicio 37

$z^3−27$

Contestar: $(z−3)(z^2+3z+9)$

Ejercicio 38

$v^3−216$

Ejercicio 39

$8−343t^3$

Contestar: $(2−7t)(4+14t+49t^2)$

Ejercicio 40

$125−27w^3$

Ejercicio 41

$8y^3−125z^3$

Contestar: $(2y−5z)(4y^2+10yz+25z^2)$

Ejercicio 42

$27x^3−64y^3$

Ejercicio 43

$7k^3+56$

Contestar: $7(k+2)(k^2−2k+4)$

Ejercicio 44

$6x^3−48y^3$

Ejercicio 45

$2−16y^3$

Contestar: $2(1−2y)(1+2y+4y^2)$

Ejercicio 46

$−2x^3−16y^3$

Práctica Mixta

En los siguientes ejercicios, factor.

Ejercicio 47

$64a^2−25$

Contestar: $(8a−5)(8a+5)$

Ejercicio 48

$121x^2−144$

Ejercicio 49

$27q^2−3$

Contestar: $3(3q−1)(3q+1)$

Ejercicio 50

$4p^2−100$

Ejercicio 51

$16x^2−72x+81$

Contestar: $(4x−9)^2$

Ejercicio 52

$36y^2+12y+1$

Ejercicio 53

$8p^2+2$

Contestar: $2(4p^2+1)^2$

Ejercicio 54

$81x^2+169$

Ejercicio 55

$125−8y^3$

Contestar: $(5−2y)(25+10y+4y^2)$

Ejercicio 56

$27u^3+1000$

Ejercicio 57

$45n^2+60n+20$

Contestar: $5(3n+2)^2$

Ejercicio 58

$48q^3−24q^2+3q$

Matemáticas cotidianas

Ejercicio 59

Paisajismo Sue y Alan planean poner una piscina de$15$ pies cuadrados en su patio trasero. Rodearán la alberca con una cubierta de azulejos, del mismo ancho en todos los lados. Si el ancho de la cubierta es$w$, el área total de la alberca y cubierta viene dada por el trinomio$4w^2+60w+225$.

Contestar: $(2w+15)^2$

Ejercicio 60

Reparación del hogar La altura que una escalera de doce pies puede alcanzar hasta el costado de un edificio si la base de la escalera está a$b$ pies del edificio es la raíz cuadrada del binomio$144−b^2$.

Ejercicios de escritura

Ejercicio 61

¿Por qué era importante practicar el uso del patrón de cuadrados binomiales en el capítulo de multiplicación de polinomios?

Contestar: Las respuestas pueden variar.

Ejercicio 62

¿Cómo se reconoce el patrón de cuadrados binomiales?

Ejercicio 63

Explique por qué$n^2+25 \ne (n+5)^2$.

Contestar: Las respuestas pueden variar.

Ejercicio 64

Maribel factorizado$y^2−30y+81$ como (y−9) ^2. ¿Cómo sabes que esto es incorrecto?

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

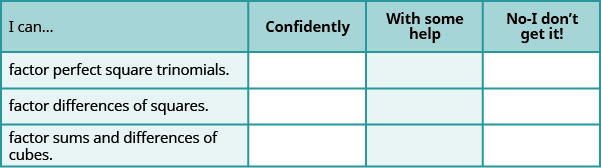
$Esta tabla tiene las siguientes declaraciones todas para ir precedidas de “Puedo...”. La primera fila es “trinomios cuadrados perfectos factorizados”. La segunda fila es “diferencias factoriales de cuadrados”. La tercera fila es “sumas de factores y diferencias de cubos”. En las columnas al lado de estas declaraciones están los encabezados, “confiadamente”, “con alguna ayuda”, y “¡No-no lo entiendo!”.$

b. En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?