8.1: Simplificar expresiones racionales
- Page ID
- 110317
Al final de esta sección, podrás:
- Determinar los valores para los que una expresión racional es indefinida
- Evaluar expresiones racionales
- Simplificar expresiones racionales
- Simplificar expresiones racionales con factores opuestos
Antes de comenzar, toma este cuestionario de preparación.
Si pierdes algún problema, vuelve a la sección listada y revisa el material.
En el Capítulo 1, revisamos las propiedades de las fracciones y sus operaciones. Introdujimos números racionales, que son solo fracciones donde los numeradores y denominadores son enteros, y el denominador no es cero.
En este capítulo, trabajaremos con fracciones cuyos numeradores y denominadores son polinomios. A estas expresiones racionales las llamamos.
Una expresión racional es una expresión de la forma\(\frac{p(x)}{q(x)}\), donde p y q son polinomios y\(q \ne 0\).
Aquí hay algunos ejemplos de expresiones racionales:
\[\begin{array}{cccc} {−\frac{13}{42}}&{\frac{7y}{8z}}&{\frac{5x+2}{x^2−7}}&{\frac{4x^2+3x−1}{2x−8}}\\ \nonumber \end{array}\]
Observe que la primera expresión racional enumerada anteriormente\(−\frac{13}{42}\),, es apenas una fracción. Dado que una constante es un polinomio con grado cero, la relación de dos constantes es una expresión racional, siempre que el denominador no sea cero.
Realizaremos las mismas operaciones con expresiones racionales que hacemos con fracciones. Simplificaremos, sumaremos, restaremos, multiplicaremos, dividiremos y los usaremos en aplicaciones.
Determinar los valores para los cuales no está definida una expresión racional
Cuando trabajamos con una fracción numérica, es fácil evitar dividir por cero, porque podemos ver el número en el denominador. Para evitar dividir por cero en una expresión racional, no debemos permitir valores de la variable que harán que el denominador sea cero.
Si el denominador es cero, la expresión racional es indefinida. El numerador de una expresión racional puede ser 0, pero no el denominador.
Entonces, antes de comenzar cualquier operación con una expresión racional, la examinamos primero para encontrar los valores que harían cero al denominador. De esa manera, cuando resolvamos una ecuación racional por ejemplo, sabremos si las soluciones algebraicas que encontremos están permitidas o no.
- Establezca el denominador igual a cero.
- Resuelve la ecuación en el conjunto de reales, si es posible.
Determinar los valores para los que la expresión racional es indefinida:
- \(\frac{9y}{x}\)
- \(\frac{4b−3}{2b+5}\)
- \(\frac{x+4}{x^2+5x+6x}\)
Solución
La expresión quedará indefinida cuando el denominador sea cero.
| 1. | \(\frac{9y}{x}\) |
| Establezca el denominador igual a cero. Resolver para la variable. | x=0 |
| \(\frac{9y}{x}\)es undefined para x=0. | |
| 2. |
\(\frac{4b−3}{2b+5}\) |
| Establezca el denominador igual a cero. Resolver para la variable. | 2b+5=0 |
| 2b=−5 | |
| \(b=−\frac{5}{2}\) | |
| \(\frac{4b−3}{2b+5}\)no está definido para\(b=−\frac{5}{2}\). | |
| 3. | \(\frac{x+4}{x^2+5x+6x}\) |
| Establezca el denominador igual a cero. Resolver para la variable. | \(x^2+5x+6x=0\) |
| \((x+2)(x+3)=0\) | |
| x+2=0 o x+3=0 | |
| x=−2 o x=−3 | |
| \(\frac{x+4}{x^2+5x+6x}\)no está definido para x=−2 o x=−3. |
Decir que la expresión racional\(\frac{x+4}{x^2+5x+6x}\) es indefinida para x=−2orx=−3 es similar a escribir la frase “void where prohibido” en las reglas del concurso.
Pruébalo\(\PageIndex{2}\)
Determinar los valores para los que la expresión racional es indefinida:
- \(\frac{3y}{x}\)
- \(\frac{8n−5}{3n+1}\)
- \(\frac{a+10}{a^2+4a+3a}\)
- Answer
-
- x=0
- \(n=−\frac{1}{3}\)
- a=−1, a=−3
Try It \(\PageIndex{3}\)
Determinar los valores para los que la expresión racional es indefinida:
- \(\frac{4p}{5q}\)
- \(\frac{y−1}{3y+2}\)
- \(\frac{m−5}{m^2+m−6}\)
- Contestar
-
- q=0
- \(y=−\frac{2}{3}\)
- m=2, m=−3
Evaluar expresiones racionales
Para evaluar una expresión racional, sustituimos valores de las variables en la expresión y simplificamos, tal como lo hemos hecho para muchas otras expresiones en este libro.
Evaluar\(\frac{2x+3}{3x−5}\) para cada valor:
- x=0
- x=2
- x=−3
Solución
| 1. |  |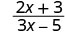
 |
 |
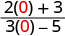| Simplificar. |  |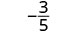
| 2. |  |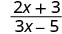
 |
 |
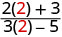| Simplificar. |  |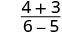
 |
|
 |
|
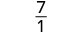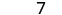| 3. |  |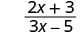
 |
 |
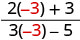| Simplificar. |  |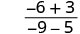
 |
|
 |
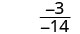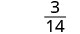Pruébalo\(\PageIndex{5}\)
Evaluar\(\frac{y+1}{2y−3}\) for each value:
- y=1
- y=−3
- y=0
- Answer
-
- −2
- \(\frac{2}{9}\)
- \(−\frac{1}{3}\)
Try It \(\PageIndex{6}\)
Evaluar\(\frac{5x−1}{2x+1}\) para cada valor:
- x=1
- x=−1
- x=0
- Contestar
-
- \(\frac{4}{3}\)
- 6
- −1
Evaluar\(\frac{x^2+8x+7}{x^2−4}\) para cada valor:
- x=0
- x=2
- x=−1
Solución
| 1. |  |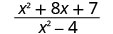
 |
 |
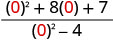| Simplificar. |  |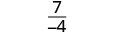
 |
|
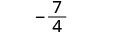| 2. | |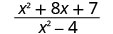
 |
 |
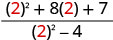| Simplificar. |  |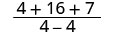
 |
|
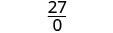| Esta expresión racional es indefinida para x = 2. | |
| 3. |  |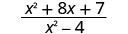
 |
 |
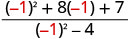| Simplificar. |  |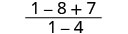
 |
|
 |
|
 |
|
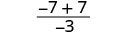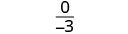Pruébalo\(\PageIndex{8}\)
Evaluar\(\frac{x^2+1}{x^2−3x+2}\) for each value:
- x=0
- x=−1
- x=3
- Answer
-
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- 2
Try It \(\PageIndex{9}\)
Evaluar\(\frac{x^2+x−6}{x^2−9}\) para cada valor.
- x=0
- x=−2
- x=1
- Contestar
-
- \(\frac{2}{3}\)
- \(\frac{4}{5}\)
- \(\frac{1}{2}\)
Recuerda que una fracción se simplifica cuando no tiene factores comunes, distintos a 1, en su numerador y denominador. Cuando evaluamos una expresión racional, nos aseguramos de simplificar la fracción resultante.
Evaluar\(\frac{a^2+2ab+b^2}{3ab}\) para cada valor.
- a=1, b=2
- a=−2, b=−1
- \(a=\frac{1}{3}\), b=0
Solución
| 1. | \(\frac{a^2+2ab+b^2}{3ab}\)cuando a=1, b=2 |
 |
 |
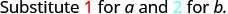| Simplificar. |  |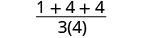
 |
|
 |
|
| 2. | \(\frac{a^2+2ab+b^2}{3ab}\)cuando a=−2, b=−1 |
 |
 |
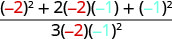| Simplificar. |  |
 |
|
 |
|
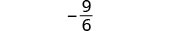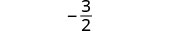| 3. | \(\frac{a^2+2ab+b^2}{3ab}\)cuando\(a=\frac{1}{3}\), b=0 |
 |
 |
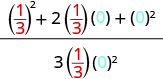| Simplificar. |  |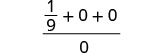
 |
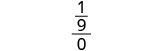Pruébalo\(\PageIndex{11}\)
Evaluar\(\frac{2a^{3}b}{a^2+2ab+b^2}\) for each value.
- a=−1, b=2
- a=0, b=−1
- a=1, \(b=\frac{1}{2}\)
- Answer
-
- −4
- 0
- \(\frac{4}{9}\)
Try It \(\PageIndex{12}\)
Evaluar\(\frac{a^2−b^2}{8ab^3}\) para cada valor:
- a=1, b=−1
- \(a=\frac{1}{2}\), b=−1
- a=−2, b=1
- Contestar
-
- 0
- \(\frac{3}{16}\)
- \(\frac{3}{16}\)
Simplificar expresiones racionales
Al igual que una fracción se considera simplificada si no hay factores comunes, distintos de 1, en su numerador y denominador, una expresión racional se simplifica si no tiene factores comunes, distintos de 1, en su numerador y denominador.
Una expresión racional se considera simplificada si no hay factores comunes en su numerador y denominador.
Por ejemplo:
- \(\frac{2}{3}\)se simplifica porque no hay factores comunes de 2 y 3.
- \(\frac{2x}{3x}\)no se simplifica porque x es un factor común de 2 x y 3 x.
Utilizamos la Propiedad de Fracciones Equivalentes para simplificar fracciones numéricas. Lo reafirmamos aquí ya que también lo usaremos para simplificar la expresión racional s.
Si a, b y c son números donde\(b \ne 0\),\(c\ne 0\), entonces\(\frac{a}{b}=\frac{a·c}{b·c}\) y\(\frac{a·c}{b·c}=\frac{a}{b}\)
Observe que en la Propiedad de Fracciones Equivalentes, los valores que harían cero a los denominadores son específicamente despermitidos. Vemos\(b \ne 0\),\(c\ne 0\) claramente enunciado. Cada vez que escribimos una expresión racional, deberíamos hacer una declaración similar desautorizando valores que harían un denominador cero. No obstante, para centrarnos en el trabajo que nos ocupa, omitiremos escribirlo en los ejemplos.
Empecemos por revisar cómo simplificamos las fracciones numéricas.
Simplificar:\(−\frac{36}{63}\).
Solución
 |
|
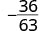| Reescribir el numerador y denominador mostrando los factores comunes. |  |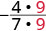
| Simplifique el uso de la propiedad de fracciones equivalentes. |  |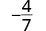
Observe que la fracción\(−\frac{4}{7}\) se simplifica porque no hay más factores comunes.
Pruébalo\(\PageIndex{14}\)
Simplificar:\(−\frac{45}{81}\).
- Answer
-
\(−\frac{5}{9}\)
Try It \(\PageIndex{15}\)
Simplificar:\(−\frac{42}{54}\).
- Contestar
-
\(−\frac{7}{9}\)
A lo largo de este capítulo, asumiremos que se excluyen todos los valores numéricos que harían que el denominador fuera cero. No vamos a escribir las restricciones para cada expresión racional, pero hay que tener en cuenta que el denominador nunca puede ser cero. Entonces en este siguiente ejemplo,\(x \ne 0\) y\(y \ne 0\).
Simplificar:\(\frac{3xy}{18x^{2}y^{2}}\).
Solución
 |
|
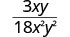| Reescribir el numerador y denominador mostrando los factores comunes. |  |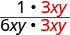
| Simplifique el uso de la propiedad de fracciones equivalentes. |  |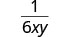
¿Se dio cuenta de que estos son los mismos pasos que dimos cuando dividimos los monomios en polinomios?
Pruébalo\(\PageIndex{17}\)
Simplificar:\(\frac{4x^{2}y}{12xy^2}\).
- Answer
-
\(\frac{x}{3y}\)
Try It \(PageIndex{18}\)
Simplificar:\(\frac{16x^{2}y}{2xy^2}\).
- Contestar
-
\(\frac{8x}{y}\)
Ten mucho cuidado ya que eliminas factores comunes. Los factores se multiplican para hacer un producto. Se puede eliminar un factor de un producto. No se puede quitar un término de una suma.
¡Ten en cuenta que eliminar las x de\(\frac{x+5}{x}\) sería como cancelar las 2 en la fracción\(\frac{2+5}{2}\)!
Cómo simplificar los binomios racionales
Simplificar:\(\frac{2x+8}{5x+20}\).
Solución
Pruébalo\(\PageIndex{20}\)
Simplificar:\(\frac{3x−6}{2x−4}\).
- Answer
-
\(\frac{3}{2}\)
Try It \(\PageIndex{21}\)
Simplificar:\(\frac{7y+35}{5y+25}\).
- Contestar
-
\(\frac{7}{5}\)
Ahora resumimos los pasos que debes seguir para simplificar las expresiones racionales.
- Facturar completamente el numerador y el denominador.
- Simplifique dividiendo los factores comunes.
Usaremos los métodos que cubrimos en Factoring para factorizar los polinomios en los numeradores y denominadores en los siguientes ejemplos.
Simplificar:\(\frac{x^2+5x+6}{x^2+8x+12}\).
Solución
| \(\frac{x^2+5x+6}{x^2+8x+12}\) | |
| Facturar el numerador y el denominador. | \(\frac{(x+2)(x+3)}{(x+2)(x+6)}\) |
| Eliminar el factor común x+2 del numerador y el denominador. | \(\frac{x+3}{x+6}\) |
¿Se puede decir qué valores de x deben excluirse en este ejemplo?
Pruébalo\(\PageIndex{23}\)
Simplificar:\(\frac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\frac{x+1}{x−1}\)
Try It \(\PageIndex{24}\)
Simplificar:\(\frac{x^2−3x−10}{x^2+x−2}\).
- Contestar
-
\(\frac{x−5}{x−1}\)
Simplificar:\(\frac{y^2+y−42}{y^2−36}\).
Solución
| \(\frac{y^2+y−42}{y^2−36}\). | |
| Facturar el numerador y el denominador. | \(\frac{(y+7)(y−6)}{(y+6)(y−6)}\) |
| Quita el factor común y−6 del numerador y del denominador. | \(\frac{y+7}{y+6}\) |
Pruébalo\(\PageIndex{26}\)
Simplificar:\(\frac{x^2+x−6}{x^2−4}\).
- Answer
-
\(\frac{x+3}{x+2}\)
Try It \(\PageIndex{27}\)
Simplificar:\(\frac{x^2+8x+7}{x^2−49}\).
- Contestar
-
\(\frac{x+1}{x−7}\)
Simplificar:\(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\).
Solución
| \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\) | |
| Factorizar el numerador y el denominador, usando agrupación para factorizar el numerador. | \(\frac{p^2(p−2)+2(p−2)}{(p−5)(p−2)}\) |
| \(\frac{(p^2+2)(p−2)}{(p−5)(p−2)}\) | |
| Elimine el factor común p−2 del numerador y del denominador. | \(\frac{p^2+2}{p−5}\) |
Pruébalo\(\PageIndex{29}\)
Simplificar:\(\frac{y^3−3y^2+y−3}{y^2−y−6}\).
- Answer
-
\(\frac{y^2+1}{y+2}\)
Try It \(\PageIndex{30}\)
Simplificar:\(\frac{p^3−p^2+2p−2}{p^2+4p−5}\).
- Contestar
-
\(\frac{p^2+2}{p+5}\)
Simplificar:\(\frac{2n^2−14n}{4n^2−16n−48}\).
Solución
| \(\frac{2n^2−14n}{4n^2−16n−48}\) | |
| Factorizar el numerador y denominador, primero factorizando el GCF. | \(\frac{2n(n−7)}{4(n^2−4n−12)}\) |
| \(\frac{2n(n−7)}{4(n−6)(n+2)}\) | |
| Eliminar el factor común, 2. | \(\frac{n(n−7)}{2(n−6)(n+2)}\) |
Pruébalo\(\PageIndex{32}\)
Simplificar:\(\frac{2n^2−10n}{4n^2−16n−20}\).
- Answer
-
\(\frac{n}{2(n+1)}\)
Try It \(\PageIndex{33}\)
Simplificar:\(\frac{4x^2−16x}{8x^2−16x−64}\).
- Contestar
-
\(\frac{x}{2(x+2)}\)
Simplificar:\(\frac{3b^2−12b+12}{6b^2−24}\).
Solución
| \(\frac{3b^2−12b+12}{6b^2−24}\) | |
| Factorizar el numerador y denominador, primero factorizando el GCF. | \(\frac{3(b^2−4b+4)}{6(b^2−4)}\) |
| \(\frac{3(b−2)(b−2)}{6(b−2)(b+2)}\) | |
| Elimine los factores comunes de b−2 y 3. | \(\frac{3(b−2)}{2(b+2)}\) |
Pruébalo\(\PageIndex{35}\)
Simplificar:\(\frac{2x^2−12x+18}{3x^2−27}\).
- Answer
-
\(\frac{2(x−3)}{3(x+3)}\)
Try It \(PageIndex{36}\)
Simplificar:\(\frac{5y^2−30y+25}{2y^2−50}\).
- Contestar
-
\(\frac{5(x−1)}{2(x+5)}\)
Simplificar:\(\frac{m^3+8}{m^2−4}\).
Solución
| \(\frac{m^3+8}{m^2−4}\) | |
| Factorizar el numerador y denominador, usando las fórmulas para suma de cubos y diferencia de cuadrados. | \(\frac{(m+2)(m^2−2m+4)}{(m+2)(m−2)}\) |
| Eliminar los factores comunes de m+2. | \(\frac{m^2−2m+4}{m−2}\) |
Pruébalo\(\PageIndex{38}\)
Simplificar:\(\frac{p^3−64}{p^2−16}\).
- Answer
-
\(\frac{p^2+4p+16}{p+4}\)
Try It \(\PageIndex{39}\)
Simplificar:\(\frac{x^3+8}{x^2−4}\).
- Contestar
-
\(\frac{x^2−2x+4}{x−2}\)
Simplifique las expresiones racionales con factores opuestos
Ahora veremos cómo simplificar una expresión racional cuyo numerador y denominador tienen factores opuestos. Empecemos con una fracción numérica, digamos\(\frac{7}{−7}\).
Sabemos que esta fracción se simplifica a −1. También reconocemos que el numerador y el denominador son opuestos.
En Fundamentos, introdujimos la notación opuesta: lo contrario de a es −a. Recordamos, también, que −a=−1·a
Simplificamos la fracción\(\frac{a}{−a}\)
\[\begin{array}{ll} {}&{\frac{a}{−a}}\\ {\text{We could rewrite this.}}&{\frac{1·a}{−1·a}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
Entonces, de la misma manera, podemos simplificar la fracción\(\frac{x−3}{−(x−3)}\)
\[\begin{array}{ll} {}&{\frac{x−3}{−(x−3)}}\\ {\text{We could rewrite this.}}&{\frac{1·(x−3)}{−1·(x−3)}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
Pero lo contrario de x−3 podría escribirse de manera diferente:
\[\begin{array}{ll} {}&{−(x−3)}\\ {\text{Distribute.}}&{−x+3}\\ {\text{Rewrite.}}&{3−x}\\ \nonumber \end{array}\]
Esto significa que la fracción\(\frac{x−3}{3−x}\) se simplifica a −1.
En general, podríamos escribir lo contrario de a−b como b−a. Entonces la expresión racional\(\frac{a−b}{b−a}\) se simplifica a −1.
Lo opuesto de a−b es b−a
\(\frac{a−b}{b−a}=−1\),\(a \ne b\)
Una expresión y su opuesto se dividen en −1
Utilizaremos esta propiedad para simplificar expresiones racionales que contienen opuestos en sus numeradores y denominadores.
Simplificar:\(\frac{x−8}{8−x}\).
Solución
| \(\frac{x−8}{8−x}\). | |
| Reconocer que x−8 y 8−x son opuestos | −1 |
Pruébalo\(\PageIndex{41}\)
Simplificar:\(\frac{y−2}{2−y}\).
- Answer
-
−1
Try It \(\PageIndex{42}\)
Simplificar:\(\frac{n−9}{9−n}\).
- Contestar
-
−1
Recuerde, el primer paso para simplificar una expresión racional es factorizar completamente el numerador y el denominador.
Simplificar:\(\frac{14−2x}{x^2−49}\).
Solución
 |
|
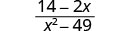| Facturar el numerador y el denominador. |  |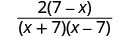
| Reconozca que 7−x y x−7 son opuestos. |  |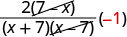
| Simplificar. |  |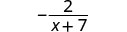
Pruébalo\(\PageIndex{44}\)
Simplificar:\(\frac{10−2y}{y^2−25}\).
- Answer
-
\(−\frac{2}{y+5}\)
Try It \(\PageIndex{45}\)
Simplificar:\(\frac{3y−27}{81−y^2}\).
- Contestar
-
\(−\frac{3}{9+y}\)
Simplificar:\(\frac{x^2−4x−32}{64−x^2}\).
Solución
 |
|
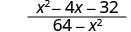| Facturar el numerador y el denominador. |  |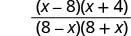
| Reconocer los factores que son opuestos. |  |
| Simplificar. |  |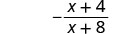
Pruébalo\(\PageIndex{47}\)
Simplificar:\(\frac{x^2−4x−5}{25−x^2}\).
- Answer
-
\(−\frac{x+1}{x+5}\)
Try It \(\PageIndex{48}\)
Simplificar:\(\frac{x^2+x−2}{1−x^2}\).
- Contestar
-
\(−\frac{x+2}{x+1}\)
Conceptos clave
- Determinar los valores para los cuales no está definida una expresión racional
- Establezca el denominador igual a cero.
- Resuelve la ecuación, si es posible.
- Expresión racional simplificada
- Una expresión racional se considera simplificada si no hay factores comunes en su numerador y denominador.
- Simplificar una expresión racional
- Facturar completamente el numerador y el denominador.
- Simplifique dividiendo los factores comunes.
- Los opuestos en una expresión racional
- Lo opuesto de a−b es b−a
\(\frac{a−b}{b−a}=−1\)\(a \ne b\)\(b \ne 0\),\(a \ne b\)
- Lo opuesto de a−b es b−a
La práctica hace la perfección
En los siguientes ejercicios, determinar los valores para los que la expresión racional es indefinida.
- \(\frac{2x}{z}\)
- \(\frac{4p−1}{6p−5}\)
- \(\frac{n−3}{n^2+2n−8}\)
- Contestar
-
- z=0
- \(p=\frac{5}{6}\)
- n=−4, n=2
- \(\frac{10m}{11n}\)
- \(\frac{6y+13}{4y−9}\)
- \(\frac{b−8}{b^2−36}\)
- \(\frac{4x^{2}y}{3y}\)
- \(\frac{3x−2}{2x+1}\)
- \(\frac{u−1}{u^2−3u−28}\)
- Contestar
-
- y=0
- \(x=−\frac{1}{2}\)
- u=−4, u=7
- \(\frac{5pq^{2}}{9q}\)
- \(\frac{7a−4}{3a+5}\)
- \(\frac{1}{x^2−4}\)
En los siguientes ejercicios, evaluar la expresión racional para los valores dados.
\(\frac{2x}{x−1}\)
- x=0
- x=2
- x=−1
- Contestar
-
- 0
- 4
- 1
\(\frac{4y−1}{5y−3}\)
- y=0
- y=2
- y=−1
\(\frac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=−2
- Contestar
-
- 3
- \(\frac{5}{2}\)
- \(−\frac{1}{5}\)
\(\frac{x+3}{2−3x}\)
- x=0
- x=1
- x=−2
\(\frac{y^2+5y+6}{y^2−1}\)
- y=0
- y=2
- y=−2
- Contestar
-
- −6
- \(\frac{20}{3}\)
- 0
\(\frac{z^2+3z−10}{z^2−1}\)
- z=0
- z=2
- z=−2
\(\frac{a^2−4}{a^2+5a+4}\)
- a=0
- a=1
- a=−2
- Contestar
-
- −1
- \(−\frac{3}{10}\)
- 0
\(\frac{b^2+2}{b^2−3b−4}\)
- b=0
- b=2
- b=−2
\(\frac{x^2+3xy+2y^2}{2x^{3}y}\)
- x=1, y=−1
- x=2, y=1
- x=−1, y=−2
- Contestar
-
- 0
- \(\frac{3}{4}\)
- \(\frac{15}{4}\)
\(\frac{c^2+cd−2d^2}{cd^{3}}\)
- c=2, d=−1
- c=1, d=−1
- c=−1, d=2
\(\frac{m^2−4n^2}{5mn^3}\)
- m=2, n=1
- m=−1, n=−1
- m=3, n=2
- Contestar
-
- 0
- \(−\frac{3}{5}\)
- \(−\frac{7}{20}\)
\(\frac{2s^{2}t}{s^2−9t^2}\)
- s=4, t=1
- s=−1, t=−1
- s=0, t=2
En los siguientes ejercicios, simplifique.
\(−\frac{4}{52}\)
- Contestar
-
\(−\frac{1}{13}\)
\(−\frac{44}{55}\)
\(\frac{56}{63}\)
- Contestar
-
\(\frac{8}{9}\)
\(\frac{65}{104}\)
\(\frac{6ab^{2}}{12a^{2}b}\)
- Contestar
-
\(\frac{b}{2ab}\)
\(\frac{15xy^{3}}{x^{3}y^{3}}\)
\(\frac{8m^{3}n}{12mn^2}\)
- Contestar
-
\(\frac{2m^2}{3n}\)
\(\frac{36v^{3}w^2}{27vw^3}\)
\(\frac{3a+6}{4a+8}\)
- Contestar
-
\(\frac{3}{4}\)
\(\frac{5b+5}{6b+6}\)
\(\frac{3c−9}{5c−15}\)
- Contestar
-
\(\frac{3}{5}\)
\(\frac{4d+8}{9d+18}\)
\(\frac{7m+63}{5m+45}\)
- Contestar
-
\(\frac{7}{5}\)
\(\frac{8n−96}{3n−36}\)
\(\frac{12p−240}{5p−100}\)
- Contestar
-
\(\frac{12}{5}\)
\(\frac{6q+210}{5q+175}\)
\(\frac{a^2−a−12}{a^2−8a+16}\)
- Contestar
-
\(\frac{a+3}{a−4}\)
\(\frac{x^2+4x−5}{x^2−2x+1}\)
\(\frac{y^2+3y−4}{y^2−6y+5}\)
- Contestar
-
\(\frac{y+4}{y−5}\)
\(\frac{v^2+8v+15}{v^2−v−12}\)
\(\frac{x^2−25}{x^2+2x−15}\)
- Contestar
-
\(\frac{x−5}{x−3}\)
\(\frac{a^2−4}{a^2+6a−16}\)
\(\frac{y^2−2y−3}{y^2−9}\)
- Contestar
-
\(\frac{y+1}{y+3}\)
\(\frac{b^2+9b+18}{b^2−36}\)
\(\frac{y^3+y^2+y+1}{y^2+2y+1}\)
- Contestar
-
\(\frac{y^2+1}{y+1}\)
\(\frac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\frac{x^3−2x^2−25x+50}{x^2−25}\)
- Contestar
-
x−2
\(\frac{q^3+3q^2−4q−12}{q^2−4}\)
\(\frac{3a^2+15a}{6a^2+6a−36}\)
- Contestar
-
\(\frac{a(a+5)}{2(a+3)(a−2)}\)
\(\frac{8b^2−32b}{2b^2−6b−80}\)
\(\frac{−5c^2−10c}{−10c^2+30c+100}\)
- Contestar
-
\(\frac{c}{2(c−5)}\)
\(\frac{4d^2−24d}{2d^2−4d−48}\)
\(\frac{3m^2+30m+75}{4m^2−100}\)
- Contestar
-
\(\frac{3(m+5)}{4(m−5)}\)
\(\frac{5n^2+30n+45}{2n^2−18}\)
\(\frac{5r^2+30r−35}{r^2−49}\)
- Contestar
-
\(\frac{5(r−1)}{r+7}\)
\(\frac{3s^2+30s+24}{3s^2−48}\)
\(\frac{t^3−27}{t^2−9}\)
- Contestar
-
\(\frac{t^2+3t+9}{t+3}\)
\(\frac{v^3−1}{v^2−1}\)
\(\frac{w^3+216}{w^2−36}\)
- Contestar
-
\(\frac{w^2−6w+36}{w−6}\)
\(\frac{v^3+125}{v^2−25}\)
Simplifique las expresiones racionales con factores opuestos
En los siguientes ejercicios, simplificar cada expresión racional.
\(\frac{a−5}{5−a}\)
- Contestar
-
−1
\(\frac{b−12}{12−b}\)
\(\frac{11−c}{c−11}\)
- Contestar
-
−1
\(\frac{5−d}{d−5}\)
\(\frac{12−2x}{x^2−36}\)
- Contestar
-
\(−\frac{2}{x+6}\)
\(\frac{20−5y}{y^2−16}\)
\(\frac{4v−32}{64−v^2}\)
- Contestar
-
\(−\frac{4}{8+v}\)
\(\frac{7w−21}{9−w^2}\)
\(\frac{y^2−11y+24}{9−y^2}\)
- Contestar
-
\(−\frac{y−8}{3+y}\)
\(\frac{z^2−9z+20}{16−z^2}\)
\(\frac{a^2−5a−36}{81−a^2}\)
- Contestar
-
\(−\frac{a+4}{9+a}\)
\(\frac{b^2+b−42}{36−b^2}\)
Matemáticas cotidianas
Tasas Fiscales Para el ejercicio fiscal 2015, el monto del impuesto adeudado por una sola persona que gana entre $37,450 y $90,750, se puede encontrar evaluando la fórmula 0.25x−4206.25, donde x es ingreso. La tasa impositiva promedio para este ingreso se puede encontrar evaluando la fórmula\(\frac{0.25x−4206.25}{x}\). ¿Cuál sería la tasa impositiva promedio para una sola persona que gana 50,000 dólares?
- Contestar
-
16.5%
Trabajo El tiempo que tardan dos personas en realizar la misma tarea si trabajan juntas se puede encontrar evaluando la fórmula\(\frac{xy}{x+y}\). Si Tom puede pintar la guarida en x=45 minutos y su hermano Bobby la puede pintar en y=60 minutos, ¿cuántos minutos les llevará si trabajan juntos?
Ejercicios de escritura
Explica cómo encuentras los valores de x para los que la expresión racional\(\frac{x^2−x−20}{x^2−4}\) es indefinida.
Explica todos los pasos que das para simplificar la expresión racional\(\frac{p^2+4p−21}{9−p^2}\).
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
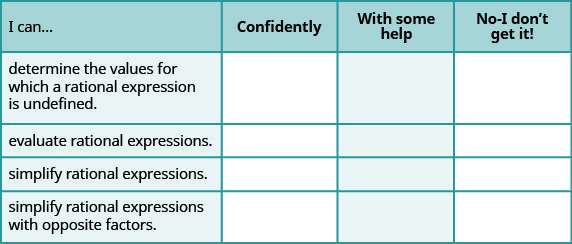
ⓑ Si la mayoría de tus cheques fueron:
... con confianza. ¡Felicidades! ¡Has logrado tus metas en esta sección! Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? ¡Sé específico!
... con alguna ayuda. Esto debe abordarse rápidamente ya que los temas que no dominas se convierten en baches en tu camino hacia el éxito. Las matemáticas son secuenciales - cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no - ¡No lo consigo! Esto es crítico y no debes ignorarlo. Necesita obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.
Glosario
- expresión racional
- Una expresión racional es una expresión de la forma\(\frac{p}{q}\), donde p y q son polinomios y\(q \ne 0\).