8.2: Multiplicar y dividir expresiones racionales
- Page ID
- 110321
Al final de esta sección, podrás:
- Multiplicar expresiones racionales
- Dividir expresiones racionales
Antes de comenzar, toma este cuestionario de preparación.
Si pierdes algún problema, vuelve a la sección listada y revisa el material.
- Multiplicar:\(\frac{14}{15}·\frac{6}{35}\).
Si te perdiste este problema, revisa el Ejercicio 1.6.13. - Dividir:\(\frac{14}{15}÷\frac{6}{35}\).
Si te perdiste este problema, revisa el Ejercicio 1.6.22. - Factor completamente:\(2x^2−98\).
Si te perdiste este problema, revisa Ejercicio 7.5.10. - Factor completamente:\(10n^3+10\).
Si te perdiste este problema, revisa el Ejercicio 7.5.19. - Factor completamente:\(10p^2−25pq−15q^2\).
Si te perdiste este problema, revisa Ejercicio 7.5.28.
Multiplicar expresiones racionales
Para multiplicar expresiones racionales, hacemos justamente lo que hicimos con fracciones numéricas. Multiplicamos los numeradores y multiplicamos los denominadores. Entonces, si hay algún factor común, los eliminamos para simplificar el resultado.
Si p, q, r, s son polinomios donde\(q \ne 0\) y\(s \ne 0\)
\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)Para multiplicar expresiones racionales, multiplicar los numeradores y multiplicar los denominadores.
Haremos el primer ejemplo con fracciones numéricas para recordarnos cómo multiplicamos fracciones sin variables.
Multiplicar:\(\frac{10}{28}·\frac{8}{15}\).
- Contestar
-
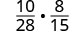
Multiplicar los numeradores y denominadores. 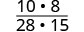
Busque factores comunes, y luego retírelos. 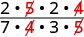
Simplificar. 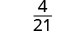
Multiplicado:\(\frac{6}{10}·\frac{15}{12}\).
- Contestar
-
\(\frac{3}{4}\)
Multiplicado:\(\frac{20}{15}·\frac{6}{8}\).
- Contestar
-
1
Recuerde, a lo largo de este capítulo, asumiremos que se excluyen todos los valores numéricos que harían que el denominador fuera cero. No vamos a escribir las restricciones para cada expresión racional, pero hay que tener en cuenta que el denominador nunca puede ser cero. Entonces, en este siguiente ejemplo,\(x \ne 0\) and \(y \ne 0\).
Multiplicado:\(\frac{2x}{3y^2}·\frac{6xy^3}{x^{2}y}\).
- Contestar
-
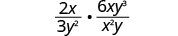
Multiplicar. 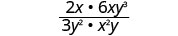
Factorizar completamente el numerador y el denominador, y luego eliminar los factores comunes. 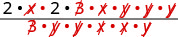
Simplificar. 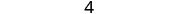
Multiplicado:\(\frac{3pq}{q^2}·\frac{5p^{2}q}{6pq}\).
- Contestar
-
\(\frac{5p^2}{2q}\)
Multiplicado:\(\frac{6x^{3}y}{7x^2}·\frac{2xy}{3x^{2}y}\).
- Contestar
-
\(\frac{12y^3}{7}\)
Cómo Multiplicar Expresiones Racionales
Multiplicado:\(\frac{2x}{x^2-7x+12}·\frac{x^2−9}{6x^2}\).
- Contestar
-
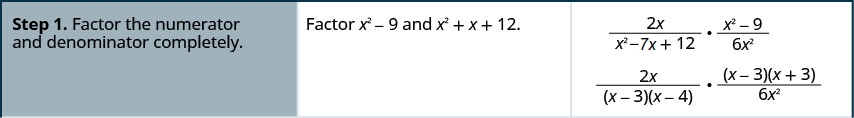


Multiplicado:\(\frac{5x}{x^2+5x+6}·\frac{x^2−4}{10x}\).
- Contestar
-
\(\frac{x−2}{2(x+3)}\)
Multiplicado:\(\frac{9x^2}{x^2+11x+30}·\frac{x^2−36}{3x^2}\).
- Contestar
-
\(\frac{3(x−6)}{x+5}\)
- Factorizar cada numerador y denominador completamente.
- Multiplicar los numeradores y denominadores.
- Simplifique dividiendo los factores comunes.
Multiplicar:\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\).
- Contestar
-
\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\) Factorizar cada numerador y denominador. \(\frac{n(n−7)}{(n+1)(n+1)}·\frac{n+1}{2n}\) Multiplicar los numeradores y los denominadores. \(\frac{n(n−7)(n+1)}{(n+1)(n+1)2n}\) Simplificar. \(\frac{n−7}{2(n+1)}\)
Multiplicar:\(\frac{x^2−25}{x^2−3x−10}·\frac{x+2}{x}\).
- Contestar
-
\(\frac{x+5}{x}\)
Multiplicar:\(\frac{x^2−4x}{x^2+5x+6}·\frac{x+2}{x}\).
- Contestar
-
\(\frac{x−4}{x+3}\)
Multiplicar:\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\).
- Contestar
-
\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\) Factorizar cada numerador y denominador. \(\frac{4(4−x)}{2(x−6)}·\frac{(x−6)(x+1)}{(x−4)(x+4)}\) Multiplicar los numeradores y los denominadores. \(\frac{4(4−x)(x−6)(x+1)}{2(x−6)(x−4)(x+4)}\) Simplificar. \(−\frac{2(x+1)}{(x+4)}\)
Multiplicar:\(\frac{12x−6x^2}{x^2+8x}·\frac{x^2+11x+24}{x^2−4}\).
- Contestar
-
\(−\frac{6(x+3)}{x+2}\)
Multiplicar:\(\frac{9v−3v^2}{9v+36}·\frac{v^2+7v+12}{v^2−9}\).
- Contestar
-
\(−\frac{v}{3}\)
Multiplicar:\(\frac{2x−6}{x^2−8x+15}·\frac{x^2−25}{2x+10}\).
- Contestar
-
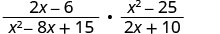
Factorizar cada numerador y denominador. 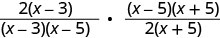
Multiplicar los numeradores y denominadores. 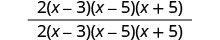
Eliminar factores comunes. 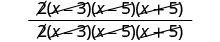
Simplificar. 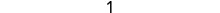
Multiplicar:\(\frac{3a−21}{a^2−9a+14}·\frac{a^2−4}{3a+6}\).
- Contestar
-
1
Multiplicar:\(\frac{b^2−b}{b^2+9b−10}·\frac{b^2−100}{b^2−10b}\).
- Contestar
-
1
Dividir expresiones racionales
Para dividir expresiones racionales multiplicamos la primera fracción por la recíproca de la segunda, tal como hicimos para las fracciones numéricas.
Recuerden, el recíproco de\(\frac{a}{b}\) es\(\frac{b}{a}\). Para encontrar el recíproco simplemente ponemos el numerador en el denominador y el denominador en el numerador. Nosotros “volteamos” la fracción.
Si p, q, r, s son polinomios donde\(q \ne 0\)\(r \ne 0\),\( s \ne 0\)
\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
Para dividir las expresiones racionales se multiplica la primera fracción por la recíproca de la segunda.
Cómo dividir expresiones racionales
Dividir:\(\frac{x+9}{6−x}÷\frac{x^2−81}{x−6}\).
- Contestar
-




Dividir:\(\frac{c+3}{5−c}÷\frac{c^2−9}{c−5}\).
- Contestar
-
\(−\frac{1}{c−3}\)
Dividir:\(\frac{2−d}{d−4}÷\frac{4−d^2}{4−d}\).
- Contestar
-
\(−\frac{1}{2+d}\)
- Reescribir la división como producto de la primera expresión racional y la recíproca de la segunda.
- Factorizar completamente los numeradores y denominadores.
- Multiplique los numeradores y denominadores juntos.
- Simplifique dividiendo los factores comunes.
Dividir:\(\frac{3n^2}{n^2−4n}÷\frac{9n^2−45n}{n^2−7n+10}\).
- Contestar
-
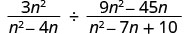
Reescribir la división como producto de la primera expresión racional y la recíproca de la segunda. 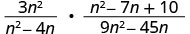
Factorizar los numeradores y denominadores y luego multiplicar. 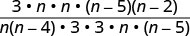
Simplifique dividiendo los factores comunes. 
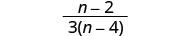
Dividir:\(\frac{2m^2}{m^2−8m}÷\frac{8m^2+24m}{m^2+m−6}\).
- Contestar
-
\(\frac{(m−2)}{4(m−8)}\)
Dividir:\(\frac{15n^2}{3n^2+33n}÷\frac{5n−5}{n^2+9n−22}\).
- Contestar
-
\(\frac{n(n−2)}{n−1}\)
Recuerde, primero reescribir la división como multiplicación de la primera expresión por el recíproco de la segunda. Entonces factorizar todo y buscar factores comunes.
Dividir:\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\).
- Contestar
-
\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\) Reescribir la división como producto de la primera expresión racional y la recíproca de la segunda. \(\frac{2x^2+5x−12}{x^2−16}·\frac{x^2−8x+16}{2x^2−13x+15}\) Factorizar los numeradores y denominadores y luego multiplicar. \(\frac{(2x−3)(x+4)(x−4)(x−4)}{(x−4)(x+4)(2x−3)(x−5)}\) Simplificar. \(\frac{(x−4)}{(x−5)}\)
Dividir:\(\frac{3a^2−8a−3}{a^2−25}÷\frac{3a^2−14a−5}{a^2+10a+25}\).
- Contestar
-
\(\frac{(a−3)(a+5)}{(a−5)(a−5)}\)
Dividir:\(\frac{4b^2+7b−2}{1−b^2}÷\frac{4b^2+15b−4}{b^2−2b+1}\).
- Contestar
-
\(−\frac{(b+2)(b−1)}{(1+b)(b+4)}\)
Dividir:\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\).
- Contestar
-
\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\) Reescribir la división como producto de la primera expresión racional y la recíproca de la segunda. \(\frac{p^3+q^3}{2p^2+2pq+2q^2}·\frac{6}{p^2−q^2}\) Factorizar los numeradores y denominadores y luego multiplicar. \(\frac{(p+q)(p^2−pq+q^2)6}{2(p^2+pq+q^2)(p−q)(p+q)}\) Simplificar. \(\frac{3(p^2−pq+q^2)}{(p−q)(p^2+pq+q^2)}\)
Dividir:\(\frac{x^3−8}{3x^2−6x+12}÷\frac{x^2−4}{6}\).
- Contestar
-
\(\frac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
Dividir:\(\frac{2z^2}{z^2−1}÷\frac{z^3−z^2+z}{z^3−1}\).
- Contestar
-
\(\frac{2z(z^2+z+1)}{(z+1)(z^2−z+1)}\)
Antes de hacer el siguiente ejemplo, veamos cómo dividimos una fracción por un número entero. Cuando dividimos\(\frac{3}{5}÷4\)
\[\begin{array}{c} {\frac{3}{5}÷4}\\ {\frac{3}{5}÷\frac{4}{1}}\\ {\frac{3}{5}·\frac{1}{4}}\\ \nonumber \end{array}\]
Hacemos lo mismo cuando dividimos expresiones racionales.
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\).
- Contestar
-
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\) Escribe la segunda expresión como una fracción. \(\frac{a^2−b^2}{3ab}÷\frac{a^2+2ab+b^2}{1}\) Reescribir la división como la primera expresión multiplicada por el recíproco de la segunda expresión. \(\frac{a^2−b^2}{3ab}·\frac{1}{a^2+2ab+b^2}\) Factorizar los numeradores y los denominadores, y luego multiplicar. \(\frac{(a−b)(a+b)1}{3ab·(a+b)(a+b)}\) Simplificar. \(\frac{a−b}{3ab(a+b)}\)
\(\frac{2x^2−14x−16}{4}÷(x2+2x+1)\).
- Contestar
-
\(\frac{x−8}{2(x+1)}\)
\(\frac{y^2−6y+8}{y^2−4y}÷(3y2−12y)\).
- Contestar
-
\(\frac{y−2}{3y(y−4)}\)
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\).
- Contestar
-
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\) Reescribir con un signo de división. \(\frac{6x^2−7x+2}{4x−8}÷\frac{2x^2−7x+3}{x^2−5x+6}\) Reescribir como producto de primeros tiempos recíprocos de segundos. \(\frac{6x^2−7x+2}{4x−8}·\frac{x^2−5x+6}{2x^2−7x+3}\) Factorizar los numeradores y los denominadores, y luego multiplicar \(\frac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)}\) Simplificar. \(\frac{3x−2}{4}\)
\(\frac{\frac{3x^2+7x+2}{4x+24}}{\frac{3x^2−14x−5}{x^2+x−30}}\).
- Contestar
-
\(\frac{x+2}{4}\)
\(\frac{\frac{y^2−36}{2y^2+11y−6}}{\frac{2y^2−2y−60}{8y−4}}\).
- Contestar
-
\(\frac{2}{y+5}\)
Si tenemos más de dos expresiones racionales con las que trabajar, seguimos el mismo procedimiento. El primer paso será reescribir cualquier división como multiplicación por lo recíproco. Entonces facetamos y multiplicamos.
\(\frac{3x−6}{4x−4}·\frac{x^2+2x−3}{x^2−3x−10}÷\frac{2x+12}{8x+16}\).
- Contestar
-
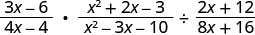
Reescribir la división como multiplicación por lo recíproco. 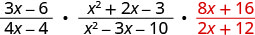
Factorizar los numeradores y los denominadores, y luego multiplicar. 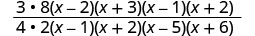
Simplifique dividiendo los factores comunes. 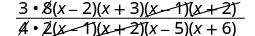
Simplificar. 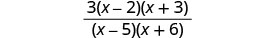
\(\frac{4m+4}{3m−15}·\frac{m^2−3m−10}{m^2−4m−32}÷\frac{12m−36}{6m−48}\).
- Contestar
-
\(\frac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
\(\frac{2n^2+10n}{n−1}÷\frac{n^2+10n+24}{n^2+8n−9}·\frac{n+4}{8n^2+12n}\).
- Contestar
-
\(\frac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
Conceptos clave
- Multiplicación de expresiones racionales
- Si p, q, r, s son polinomios donde\(q \ne 0\) y\(s \ne 0\), entonces\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)
- Multiplicar expresiones racionales, multiplicar los numeradores y multiplicar los denominadores
- Multiplicar una expresión racional
- Factorizar cada numerador y denominador completamente.
- Multiplicar los numeradores y denominadores.
- Simplifique dividiendo los factores comunes.
- División de Expresiones Racionales
- Si p, q, r, s son polinomios donde\(q \ne 0\),\(r \ne 0\),\( s \ne 0\), entonces\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
- Para dividir las expresiones racionales se multiplica la primera fracción por la recíproca de la segunda.
- Dividir expresiones racionales
- Reescribir la división como producto de la primera expresión racional y la recíproca de la segunda.
- Factorizar completamente los numeradores y denominadores.
- Multiplique los numeradores y denominadores juntos.
- Simplifique dividiendo los factores comunes.


