8.7E: Ejercicios
- Page ID
- 110284
La práctica hace la perfección
Resolver proporciones
En los siguientes ejercicios, resuelve.
\(\frac{x}{56}=\frac{7}{8}\)
- Contestar
-
\(49\)
\(\frac{n}{91}=\frac{8}{13}\)
\(\frac{49}{63}=\frac{z}{9}\)
- Contestar
-
\(7\)
\(\frac{56}{72}=\frac{y}{9}\)
\(\frac{5}{a}=\frac{65}{11}\)
- Contestar
-
\(9\)
\(\frac{4}{b}=\frac{64}{144}\)
\(\frac{98}{154}=−\frac{7}{p}\)
- Contestar
-
\(−11\)
\(\frac{72}{156}=−\frac{6}{q}\)
\(\frac{a}{−8}=\frac{−42}{48}\)
- Contestar
-
\(7\)
\(\frac{b}{−7}=\frac{−30}{42}\)
\(\frac{2.7}{j}=\frac{0.9}{0.2}\)
- Contestar
-
\(0.6\)
\(\frac{2.8}{k}=\frac{2.1}{1.5}\)
\(\frac{a}{a+12}=\frac{4}{7}\)
- Contestar
-
\(16\)
\(\frac{b}{b−16}=\frac{11}{9}\)
\(\frac{c}{c−104}=−\frac{5}{8}\)
- Contestar
-
\(−\frac{5}{8}\)
\(\frac{d}{d−48}=−\frac{13}{3}\)
\(\frac{m+90}{25}=\frac{m+30}{15}\)
- Contestar
-
\(60\)
\(\frac{n+10}{4}=\frac{40−n}{6}\)
\(\frac{2p+4}{8}=\frac{p+18}{6}\)
- Contestar
-
\(30\)
\(\frac{q−2}{2}=\frac{2q−7}{18}\)
Los pediatras prescriben 5 mililitros (ml) de acetaminofén por cada 25 libras del peso de un niño. ¿Cuántos mililitros de acetaminofén le recetará el médico a Jocelyn, quien pesa 45 libras?
- Contestar
-
9 ml
Brianna, quien pesa 6 kg, acaba de recibir sus inyecciones y necesita un analgésico. El analgésico se prescribe a los niños a 15 miligramos (mg) por cada 1 kilogramo (kg) del peso del niño. ¿Cuántos miligramos prescribirá el médico?
Un veterinario le recetó a Sunny, un perro de 65 libras, un medicamento antibacteriano en caso de que surja una infección después de limpiarse los dientes. Si la dosis es de 5 mg por cada libra, ¿cuánto medicamento le dio Sunny?
- Contestar
-
325 mg
Belle, un gato de 13 libras, sufre de dolor en las articulaciones. ¿Cuánto medicamento debe recetar el veterinario si la dosis es de 1.8 mg por libra?
Una nueva bebida energética anuncia 106 calorías por 8 onzas. ¿Cuántas calorías hay en 12 onzas de la bebida?
- Contestar
-
159 calorías
Una lata de refresco de 12 onzas tiene 150 calorías. Si Josiah bebe el tamaño grande de 32 onzas del mini-mart local, ¿cuántas calorías obtiene?
Se anuncia una nueva bebida helada de limón de 7 onzas por tener solo 140 calorías. ¿Cuántas onzas podría beber Sally si quisiera beber solo 100 calorías?
- Contestar
-
5 oz
A Reese le encanta tomar batidos verdes saludables. Una porción de batido de 16 onzas tiene 170 calorías. Reese bebe 24 onzas de estos batidos en un día. ¿Cuántas calorías de batido está consumiendo en un día?
Janice viaja a Canadá y cambiará 250 dólares estadounidenses a dólares canadienses. Al tipo de cambio actual, $1 US es igual a $1.01 canadiense. ¿Cuántos dólares canadienses obtendrá por su viaje?
- Contestar
-
252.5 Dólares canadienses
Todd viaja a México y necesita cambiar 450 dólares por pesos mexicanos. Si cada dólar vale 12.29 pesos, ¿cuántos pesos obtendrá por su viaje?
Steve cambió 600 dólares a 480 euros. ¿Cuántos euros recibió por cada dólar estadounidense?
- Contestar
-
0.80 Euros
Martha cambió 350 dólares estadounidenses a 385 dólares australianos. ¿Cuántos dólares australianos recibió por cada dólar estadounidense?
Al viajar a Gran Bretaña, Bethany cambió sus 900 dólares por 570 libras esterlinas. ¿Cuántas libras recibió por cada dólar americano?
- Contestar
-
0.63 Libras esterlinas
Un misionero comisionado a Sudáfrica tuvo que cambiar sus $500 por el Rand Sudafricano que vale 12.63 por cada dólar. ¿Cuántos Rand tenía después del intercambio?
Ronald necesita una bebida matutina para el desayuno que le dé al menos 390 calorías. El jugo de naranja tiene 130 calorías en una taza. ¿Cuántas tazas necesita beber para alcanzar su meta calórica?
- Contestar
-
3 tazas
Sarah bebe una bebida energética de 32 onzas que contiene 80 calorías por 12 onza. ¿Cuántas calorías bebió?
Elizabeth regresa a Estados Unidos desde Canadá. Ella cambia los 300 dólares canadienses restantes que tiene a $230.05 en dólares americanos. ¿Qué valía $1 en dólares canadienses?
- Contestar
-
1.30 Dólares canadienses
Ben necesita convertir $1000 al yen japonés. Un dólar americano vale 123.3 yenes. ¿Cuánto yen va a tener?
Un golden retriever que pesa 85 libras tiene diarrea. Su medicamento se prescribe como 1 cucharadita por cada 5 libras. ¿Cuánto medicamento se le debe dar?
- Contestar
-
17 cdta
Lacy, de cinco años, fue picado por una abeja. La dosis para el líquido antipicor es de 150 mg por su peso de 40 libras. ¿Cuál es la dosis por libra?
Karen come\(\frac{1}{2}\) taza de avena que cuenta 2 puntos en su programa de pérdida de peso. Su esposo, Joe, puede tomar 3 puntos de avena para desayunar. ¿Cuánta avena puede tomar?
- Contestar
-
\(\frac{3}{4}\)taza
Una receta de galleta de avena requiere una\(\frac{1}{2}\) taza de mantequilla para hacer 4 docenas de galletas. Hilda necesita hacer 10 docenas de galletas para la venta de horneados. ¿Cuántas tazas de mantequilla necesitará?
Resolver aplicaciones de figuras similares
En los siguientes ejercicios, ΔABC es similar a ΔXYZ
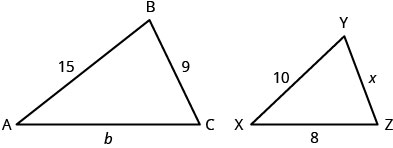
lado b
- Contestar
-
12
lado x

Encuentra la longitud del lado d.
- Contestar
-
\(\frac{77}{18}\)
Encuentra la longitud del lado q.
En los dos ejercicios siguientes, usa el mapa que se muestra. En el mapa, la ciudad de Nueva York, Chicago y Memphis forman un triángulo cuyos lados se muestran en la siguiente figura. La distancia real de Nueva York a Chicago es de 800 millas.
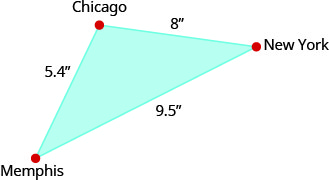
Encuentra la distancia real de Nueva York a Memphis.
- Contestar
-
950 millas
Encuentra la distancia real de Chicago a Memphis.
En los dos ejercicios siguientes, usa el mapa que se muestra. En el mapa, Atlanta, Miami y Nueva Orleans forman un triángulo cuyos lados se muestran en la siguiente figura. La distancia real de Atlanta a Nueva Orleans es de 420 millas.
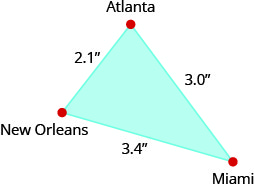
Encuentra la distancia real de Nueva Orleans a Miami.
- Contestar
-
680 millas
Encuentra la distancia real de Atlanta a Miami.
Un perro de 2 pies de altura proyecta una sombra de 3 pies al mismo tiempo que un gato proyecta una sombra de un pie. ¿Qué tan alto es el gato?
- Contestar
-
\(\frac{2}{3}\)Pie (8 pulgadas)
Larry y Tom estaban parados uno al lado del otro en el patio trasero cuando Tom desafió a Larry a adivinar qué tan alto era. Larry sabía que su propia estatura es de 6.5 pies y cuando midieron sus sombras, la sombra de Larry era de 8 pies y la de Tom tenía 7.75 pies de largo. ¿Cuál es la altura de Tom?
La porción de torre de un molino de viento mide 212 pies de altura. Una persona de seis pies de altura parada junto a la torre proyecta una sombra de siete pies. ¿Cuánto dura la sombra del molino de viento?
- Contestar
-
247.3 pies
La altura de la Estatua de la Libertad es de 305 pies. Nicole, que está parada junto a la estatua, proyecta una sombra de 6 pies y mide 5 pies de altura. ¿Cuánto tiempo debe durar la sombra de la estatua?
Matemáticas cotidianas
Ritmo Cardíaco En el gimnasio, Carol toma su pulso durante 10 segundos y cuenta 19 latidos.
- ¿Cuántos latidos por minuto es esto?
- ¿Carol ha alcanzado su ritmo cardíaco objetivo de 140 latidos por minuto?
- Contestar
-
- 114 latidos por minuto
- no
Frecuencia Cardíaca Kevin quiere mantener su ritmo cardíaco a 160 latidos por minuto mientras entrena. Durante su entrenamiento cuenta 27 latidos en 10 segundos.
- ¿Cuántos latidos por minuto es esto?
- ¿Kevin ha cumplido con su frecuencia cardíaca objetivo?
Costo de un Viaje por Carretera El auto de Jesse obtiene 30 millas por galón de gasolina.
- Si Las Vegas está a 285 millas de distancia, ¿cuántos galones de gasolina se necesitan para llegar y luego a casa?
- Si el gas es de $3.09 por galón, ¿cuál es el costo total del gas para el viaje?
- Contestar
-
- 19 galones
- $58.71
Costo de un Road Trip Danny quiere conducir hasta Phoenix para ver a su abuelo. Phoenix está a 370 millas de la casa de Danny y su auto obtiene 18.5 millas por galón.
- ¿Cuántos galones de gasolina necesitará Danny para llegar y salir de Phoenix?
- Si la gasolina es de $3.19 por galón, ¿cuál es el costo total para que la gasolina conduzca para ver a su abuelo?
Fertilizante para Césped Phil quiere fertilizar su césped. Cada bolsa de fertilizante cubre alrededor de 4,000 pies cuadrados de césped. El césped de Phil es de aproximadamente 13,500 pies cuadrados. ¿Cuántas bolsas de fertilizante tendrá que comprar?
- Contestar
-
4 bolsas
House Paint April quiere pintar el exterior de su casa. Un galón de pintura cubre aproximadamente 350 pies cuadrados, y el exterior de la casa mide aproximadamente 2000 pies cuadrados. ¿Cuántos galones de pintura tendrá que comprar?
Cocinar la receta de pasta de Natalia requiere 2 libras de pasta por 1 cuarto de salsa. ¿Cuántas libras de pasta debe cocinar Natalia si tiene 2.5 cuartos de salsa?
- Contestar
-
5
Aceite para calefacción Un tanque de aceite de 275 galones cuesta $400 para llenar. ¿Cuánto costaría llenar un tanque de aceite de 180 galones?
Ejercicios de escritura
Marisol resuelve la proporción\(\frac{144}{a}=\frac{9}{4}\) por 'multiplicación cruzada', por lo que su primer paso se ve como 4·144=9·a. Explique en qué se diferencia esto del método de solución mostrado en Ejemplo.
- Contestar
-
Las respuestas variarán.
Encuentre un mapa impreso y luego escriba y resuelva un problema de aplicación similar al Ejemplo.
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


