8.8: Resolver movimiento uniforme y aplicaciones de trabajo

Última actualización
Guardar como PDF

Page ID: 110290

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Resolver aplicaciones de movimiento uniforme
Resolver aplicaciones de trabajo

Antes de comenzar, toma este cuestionario de preparación.

Si te pierdes algún problema, vuelve a la sección listada y revisa el material.

Un tren expreso y un autobús local salen de Chicago para viajar a Champaign. El autobús express puede hacer el viaje en 2 horas y el autobús local tarda 5 horas para el viaje. La velocidad del autobús expreso es 42 millas por hora más rápida que la velocidad del autobús local. Encuentra la velocidad del autobús local.
Si te perdiste este problema, revisa [enlace].
Resolver$\frac{1}{3}x+\frac{1}{4}x=\frac{5}{6}$.
Si te perdiste este problema, revisa [enlace].
Resolver:$18t^2−30=−33t$.
Si te perdiste este problema, revisa [enlace].

Resolver aplicaciones de movimiento uniforme

Hemos resuelto problemas de movimiento uniforme utilizando la fórmula D=RT en capítulos anteriores. Utilizamos una tabla como la de abajo para organizar la información y llevarnos a la ecuación.

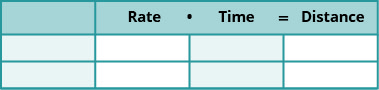
$La imagen de arriba es una tabla con 4 columnas y tres filas. La primera fila es la fila de encabezado. La segunda columna de la fila de encabezado tiene la palabra “tasa”. La tercera columna tiene la palabra, “Tiempo”. La cuarta columna dice “Distancia”. El resto de los espacios están en blanco.$

La fórmula d=RT supone que conocemos r y t y los usamos para encontrar D. Si conocemos D y r y necesitamos encontrar t, resolveríamos la ecuación para t y obtendríamos la fórmula$t=\frac{D}{r}$

También hemos explicado cómo volar con o contra una corriente afecta la velocidad de un vehículo. Volveremos a visitar esa idea en el siguiente ejemplo.

Ejemplo$\PageIndex{1}$

Un avión puede volar 200 millas en un viento en contra de 30 mph en la misma cantidad de tiempo que lleva volar 300 millas con un viento de cola de 30 mph. ¿Cuál es la velocidad del avión?

Solución

Esta es una situación de movimiento uniforme. Un diagrama nos ayudará a visualizar la situación.

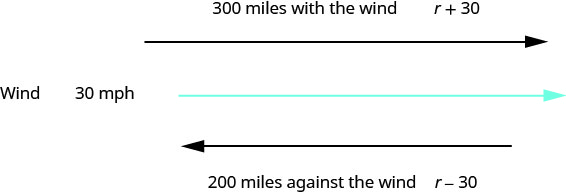
$La imagen de arriba tiene dos flechas paralelas. La primera flecha tiene su punta apuntando a la derecha Las palabras,” 300 millas con el viento r más 30” por encima de la punta de la flecha. Debajo de eso hay una línea squiggly. A la izquierda de la línea squiggly dice: “Viento 30 millas por hora”. Debajo de eso hay una flecha con su punta apuntando hacia la izquierda. Debajo de eso están las palabras, “200 millas contra el viento r menos 30”.$

Rellenamos la tabla para organizar la información.

Estamos buscando la velocidad del avión.	Deja que r= la velocidad del avión.
Cuando el avión vuela con el viento, el viento aumenta su velocidad y la velocidad es r+30.
Cuando el avión vuela contra el viento, el viento disminuye su velocidad y la velocidad es r−30.
Escribe en las tarifas. Escribe en las distancias. Desde d=r∙t, resolvemos para t y obtenemos$\frac{D}{r}$. Dividimos la distancia por la tasa en cada fila, y colocamos la expresión en la columna de tiempo.	$.$
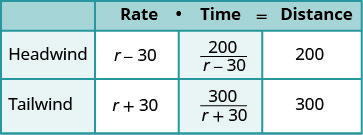Sabemos que los tiempos son iguales y así escribimos nuestra ecuación.	$\frac{200}{r−30}=\frac{300}{r+30}$
Multiplicamos ambos lados por el LCD. 200 (r+30) =300 (r−30)
Simplificar.	(r+30) (200) = (r−30) (300)
	200r+6000=300r−9000
Resolver.	15000=100r 150=r
Cheque.
¿Es 150 mph una velocidad razonable para un avión? Sí. Si el avión viaja 150 mph y el viento es de 30 mph:
Viento de cola 150+30=180 mph$\frac{300}{180}=\frac{5}{3}$ horas
Viento en contra 150−30=120 mph$\frac{200}{120}=\frac{5}{3}$ horas
Los tiempos son iguales, por lo que comprueba.	El avión viajaba 150 mph.

Pruébalo$\PageIndex{2}$

Link puede montar su bicicleta 20 millas en un viento en contra de 3 mph en la misma cantidad de tiempo que puede recorrer 30 millas con un viento de cola de 3 mph. ¿Cuál es la velocidad de ciclismo de Link?

Contestar: 15 mph

Pruébalo$\PageIndex{3}$

Judy puede navegar su bote 5 millas en un viento en contra de 7 mph en la misma cantidad de tiempo que puede navegar 12 millas con un viento de cola de 7 mph. ¿Cuál es la velocidad del barco de Judy sin viento?

Contestar: 17 mph

En el siguiente ejemplo, conoceremos el tiempo total resultante de recorrer diferentes distancias a diferentes velocidades.

Ejemplo$\PageIndex{4}$

Jazmine entrenó durante 3 horas el sábado. Corrió 8 millas y luego viajó en bicicleta 24 millas. Su velocidad de ciclismo es 4 mph más rápida que su velocidad de carrera. ¿Cuál es su velocidad de carrera?

Solución

Esta es una situación de movimiento uniforme. Un diagrama nos ayudará a visualizar la situación.

$La imagen de arriba es una línea recta con dos puntas de flecha apuntando a la derecha. En el extremo izquierdo, por encima de la línea, se lee, “corre” y más abajo, un poco más allá de la primera flecha, se lee, “bicicleta”. Ligeramente por debajo de la línea, hacia el extremo izquierdo, antes de la primera flecha, se lee, “8 millas” y al extremo derecho, después de la primera flecha se lee, “12 millas”. La región desde el extremo izquierdo hasta el extremo derecho de la flecha se agrupa para indicar que toda la longitud de la línea es de 3 horas.$

Rellenamos la tabla para organizar la información.

Estamos buscando la velocidad de carrera de Jazmine.	Let r= Jazmine's running sp
Su velocidad de ciclismo es 4 millas más rápida que su velocidad de carrera.	r+4 = su velocidad de ciclismo
Se dan las distancias, ingréselas en el gráfico.
Desde d=r∙t, resolvemos para t y obtenemos$t=\frac{D}{r}$ Dividimos la distancia por la tasa en cada fila, y colocamos la expresión en la columna de tiempo.	$.$
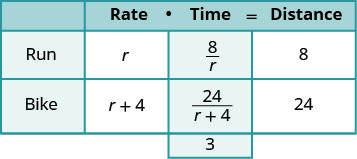Escribe una frase de palabra.	Su tiempo más el tiempo en bicicleta
Traduzca la oración para obtener la ecuación.	$\frac{8}{r}+\frac{24}{r+4}=3$
Resolver.	$r(r+4)(\frac{8}{r}+\frac{24}{r+4})=3r(r+4)$ $8(r+4)+24r=3r^2+12r$ $8r+32+24r=3r^2+12r$ $32+32r=3r^2+12r$ $0=3r^2−20r−32$ $0=(3r+4)(r−8)$
	(3r+4) =0, (r−8) =0
	$r=−\frac{4}{3}$, r=8
Comprobar. r=8
Una velocidad negativa no tiene sentido en este problema, por lo que r=8 es la solución.
¿8 mph es una velocidad de carrera razonable? Sí.
Corre 8 mph,$\frac{8 miles}{8 mph}=1 hour$ Bicicleta 12 mph,$\frac{24 miles}{12 mph}=2 hours$ Total 3 horas. La velocidad de carrera de Jazmine es de 8 mph.

Pruébalo$\PageIndex{5}$

Dennis fue a esquiar a campo traviesa durante 6 horas el sábado. Esquió 20 millas cuesta arriba y luego 20 millas atrás cuesta abajo, volviendo a su punto de partida. Su velocidad cuesta arriba era 5 mph más lenta que su velocidad cuesta abajo. ¿Cuál era la velocidad de Dennis subiendo y su velocidad bajando?

Contestar: 10 mph

Pruébalo$\PageIndex{6}$

Tony condujo 4 horas hasta su casa, manejando 208 millas en la interestatal y 40 millas en caminos rurales. Si manejaba 15 mph más rápido en la interestatal que en las carreteras rurales, ¿cuál era su tasa en las carreteras rurales?

Contestar: 50 mph

Una vez más, utilizaremos la fórmula de movimiento uniforme resuelta para la variable t.

Ejemplo$\PageIndex{7}$

Hamilton montó su bicicleta cuesta abajo 12 millas por el sendero del río desde su casa hasta el océano y luego montó cuesta arriba para regresar a casa. Su velocidad cuesta arriba era 8 millas por hora más lenta que su velocidad cuesta abajo. Le tomó 2 horas más llegar a casa de lo que le llevó llegar al océano. Encuentra la velocidad de descenso de Hamilton.

Solución

Esta es una situación de movimiento uniforme. Un diagrama nos ayudará a visualizar la situación.

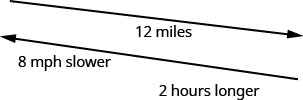
$La figura anterior muestra 2 líneas diagonales paralelas que apuntan en direcciones opuestas. La línea superior apunta hacia la derecha, y hacia abajo y tiene “12 millas” escritas debajo de ella. La línea de fondo apunta hacia la izquierda y hacia arriba, y tiene, “8 millas por hora más lento, 2 horas más” escrito debajo de ella.$

Rellenamos la tabla para organizar la información.

Estamos buscando la velocidad de descenso de Hamilton.	Deja que r= la velocidad de descenso de Hamilton.
Su velocidad cuesta arriba es de 8 millas por hora más lenta. Ingresa las tarifas en el gráfico.	h−8= Velocidad cuesta arriba de Hamilton
La distancia es la misma en ambos sentidos, 12 millas. Desde d=r∙t, resolvemos para t y obtenemos$t=\frac{D}{r}$ Dividimos la distancia por la tasa en cada fila, y colocamos la expresión en la columna de tiempo.	$.$
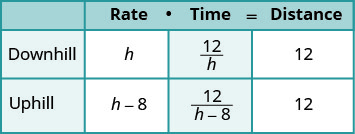Escribe una frase de palabras sobre la hora.	Tomó 2 horas más cuesta arriba que cuesta abajo. El tiempo cuesta arriba es 2 más que el tiempo de descenso.
Traduzca la oración para obtener la ecuación. Resolver.	$\frac{12}{h−8}=\frac{12}{h}+2$ $h(h−8)(\frac{12}{h−8})=h(h−8)(\frac{12}{h}+2)$ 12h=12 (h−8) +2h (h−8) $12h=12h−96+2h^2−16h$ $0=2h^2−16h−96$ $0=2(h^2−8h−48)$ 0=2 (h−12) (h+4) h−12=0, h+4 = 0 h=12, h=−4
Cheque. ¿Es 12 mph una velocidad razonable para andar en bicicleta cuesta abajo? Sí.
Cuesta abajo 12 mph, $\frac{12 miles}{12 mph}=1 hour$
Cuesta arriba 12−8=4 mph $\frac{12 miles}{4 mph}=3 hours$
	El tiempo cuesta arriba es 2 horas más que el tiempo de descenso. La velocidad de descenso de Hamilton es de 12 mph.

Pruébalo$\PageIndex{8}$

Kayla montó su bicicleta a 75 millas a casa desde la universidad un fin de semana y luego viajó en autobús de regreso a la universidad. Le tomó 2 horas menos regresar a la universidad en el autobús de lo que le tomó viajar a casa en su bicicleta, y la velocidad promedio del autobús era 10 millas por hora más rápida que la velocidad de Kayla en bicicleta. Encuentra la velocidad de ciclismo de Kayla.

Contestar: 15 mph

Pruébalo$\PageIndex{9}$

Victoria corre 12 millas hasta el parque a lo largo de un sendero plano y luego regresa trotando en un sendero montañoso de 18 millas. Ella corre 1 milla por hora más lenta en el sendero montañoso que en el sendero plano, y su viaje de regreso le lleva dos horas más. Encuentra su tasa de trotar en el sendero plano.

Contestar: 6 mph

Resolver aplicaciones de trabajo

Supongamos que Pete puede pintar una habitación en 10 horas. Si trabaja a ritmo constante, en 1 hora pintaría$\frac{1}{10}$ de la habitación. Si Alicia tardaría 8 horas en pintar la misma habitación, entonces en 1 hora pintaría$\frac{1}{8}$ de la habitación. ¿Cuánto tiempo tardarían a Pete y Alicia en pintar la habitación si trabajaban juntos (y no interfirieran con el progreso del otro)?

Esta es una aplicación típica de 'trabajo'. Aquí hay tres cantidades involucradas: el tiempo que tomaría a cada una de las dos personas hacer el trabajo sola y el tiempo que les tomaría hacer el trabajo juntas.

Volvamos a Pete y Alicia pintando la habitación. Dejaremos que t sea el número de horas que les llevaría pintar la habitación juntos. Por lo que en 1 hora trabajando juntos han concluido$\frac{1}{t}$ el trabajo.

En una hora Pete hizo$\frac{1}{10}$ del trabajo. Alicia hizo$\frac{1}{8}$ del trabajo. Y juntos hicieron$\frac{1}{t}$ del trabajo.

Podemos modelar esto con la ecuación de la palabra y luego traducirlo a una ecuación racional. Para encontrar el tiempo que les llevaría si trabajaran juntos, resolvemos para t.

	$.$
	$.$
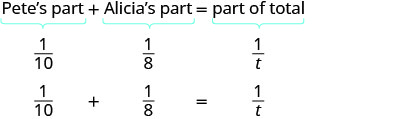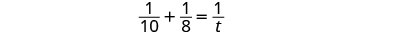Multiplicar por la pantalla LCD, 40t	$.$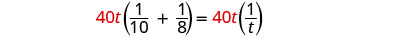
Distribuir.	$.$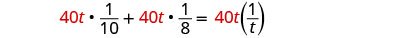
Simplifique y resuelva.	$.$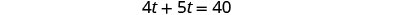
	$.$
	$.$
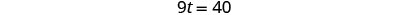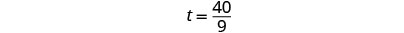Escribiremos como un número mixto para que podamos convertirlo en horas y minutos.	$.$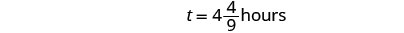
Recuerda, 1 hora = 60 minutos.	$.$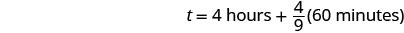
Multiplicar, y luego redondear al minuto más cercano.	$.$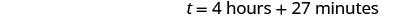
	Pete y Alica tardarían unas 4 horas y 27 minutos en pintar la habitación.

Ten en cuenta que dos personas deben tardar menos tiempo en completar un trabajo trabajando juntas que para que cualquiera de las personas lo haga sola.

Ejemplo$\PageIndex{10}$

La revista semanal de chismes tiene una gran historia sobre el bebé de la Princesa y el editor quiere que la revista se imprima lo antes posible. Ella le ha pedido a la impresora que ejecute una imprenta extra para que la impresión se haga más rápidamente. Press #1 tarda 6 horas en hacer el trabajo y Press #2 tarda 12 horas en hacer el trabajo. ¿Cuánto tiempo tardará la impresora en imprimir la revista con ambas prensas funcionando juntas?

Solución

Este es un problema de trabajo. Un gráfico nos ayudará a organizar la información.

Deje que t= la cantidad de horas necesarias para completar el trabajo juntos.
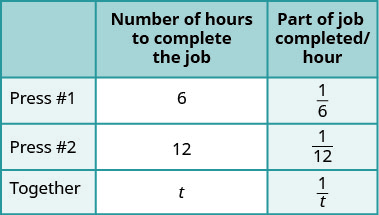Ingresa las horas por trabajo para Prensa #1, Prensa #2 y cuando trabajen juntos. Si un trabajo en Prensa #1 tarda 6 horas, entonces en 1 hora$\frac{1}{6}$ del trabajo se completa. De igual manera encontrar la parte del trabajo completado/horas para Prensa #2 y cuando ambos trabajan juntos.	$.$
Escribe una frase de palabra.
La parte completada por Prensa #1 más la parte completada por Prensa #2 equivale a la cantidad completada en conjunto.
Traducir a una ecuación.	$.$
Resolver.	$.$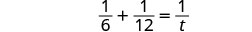
Multiplicar por el LCD, 12t.	$.$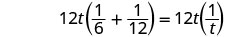
Simplificar.	$.$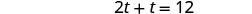
	$.$
	$.$
	Cuando ambas prensas están funcionando, se necesitan 4 horas para hacer el trabajo.

Pruébalo$\PageIndex{11}$

Un jardinero puede cortar un campo de golf en 4 horas, mientras que otro jardinero puede cortar el mismo campo de golf en 6 horas. ¿Cuánto tiempo tardaría si los dos jardineros trabajaran juntos para segar el campo de golf?

Contestar: 2 horas y 24 minutos

Pruébalo$\PageIndex{12}$

Carrie puede desyerbar el jardín en 7 horas, mientras que su madre puede hacerlo en 3. ¿Cuánto tiempo les llevará a los dos trabajar juntos?

Contestar: 2 horas y 6 minutos

Ejemplo$\PageIndex{13}$

Corey puede palear toda la nieve desde la acera y el camino de entrada en 4 horas. Si él y su gemelo Casey trabajan juntos, pueden terminar de palear la nieve en 2 horas. ¿Cuántas horas le tomaría a Casey hacer el trabajo solo?

Solución

Esta es una aplicación de trabajo. Un gráfico nos ayudará a organizar la información.
Estamos buscando cuántas horas le tomaría a Casey completar el trabajo por sí mismo.
Deja que t= la cantidad de horas necesarias para que Casey complete.
Ingresa las horas por trabajo para Corey, Casey, y cuando trabajan juntos. Si Corey tarda 4 horas, entonces en 1 hora$\frac{1}{4}$ del trabajo se termina. De igual manera encontrar la parte del trabajo completado/horas para Casey y cuando ambos trabajan juntos.	$.$
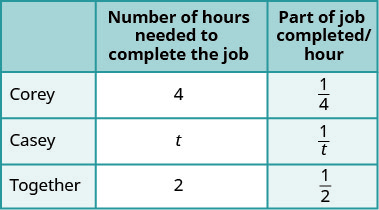Escribe una frase de palabra.
La parte completada por Corey más la parte completada por Casey equivale a la cantidad concluida en conjunto.
Traduzca a una ecuación:	$.$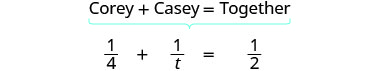
Resolver.	$.$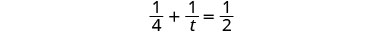
Multiplicar por la pantalla LCD, 4t.	$.$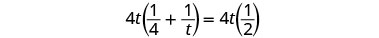
Simplificar.	$.$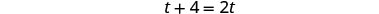
	$.$
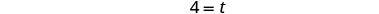	Casey tardaría 4 horas en hacer el trabajo solo.

Pruébalo$\PageIndex{14}$

Dos mangueras pueden llenar una piscina en 10 horas. Tardaría una manguera 26 horas en llenar la alberca por sí sola. ¿Cuánto tiempo tardaría la otra manguera, trabajando sola, en llenar la alberca?

Contestar: 16.25 horas

Pruébalo$\PageIndex{15}$

Cara y Cindy, trabajando juntos, pueden rastrillar el patio en 4 horas. Trabajando sola, Cindy tarda 6 horas en rastrillar el patio. ¿Cuánto tardaría Cara en rastrillar el patio sola?

Contestar: 12 horas

La práctica hace la perfección

Resolver aplicaciones de movimiento uniforme

En los siguientes ejercicios, resuelva aplicaciones de movimiento uniforme

Pruébalo$\PageIndex{16}$

Mary realiza un recorrido turístico en un helicóptero que puede volar 450 millas contra un viento en contra de 35 mph en la misma cantidad de tiempo que puede viajar 702 millas con un viento de cola de 35 mph. Encuentra la velocidad del helicóptero.

Solución

160 mph

Ejercicio$\PageIndex{17}$

Un jet privado puede volar 1210 millas contra un viento en contra de 25 mph en la misma cantidad de tiempo que puede volar 1694 millas con un viento de cola de 25 mph. Encuentra la velocidad del jet.

Pruébalo$\PageIndex{18}$

Un barco viaja 140 millas río abajo al mismo tiempo que viaja 92 millas río arriba. La velocidad de la corriente es de 6mph. ¿Cuál es la velocidad de la embarcación?

Contestar: 29 mph

Ejercicio$\PageIndex{19}$

Darrin puede monopatinar 2 millas contra un viento de 4 mph en la misma cantidad de tiempo que patina 6 millas con un viento de 4 mph. Encuentra las patinetas Darrin de velocidad sin viento.

Pruébalo$\PageIndex{20}$

Jane pasó 2 horas explorando una montaña con una moto de cross. Cuando montó las 40 millas cuesta arriba, fue 5 mph más lenta que cuando llegó al pico y cabalgó 12 millas a lo largo de la cumbre. ¿Cuál era su ritmo a lo largo de la cumbre?

Contestar: 30 mph

Ejercicio$\PageIndex{21}$

Jill quería perder algo de peso así que planeó un día de ejercicio. Pasó un total de 2 horas montando su bicicleta y trotando. Ella viajó en bicicleta por 12 millas y trotó por 6 millas. Su tarifa para trotar era de 10 mph menos que la tasa de ciclismo. ¿Cuál era su tarifa al trotar?

Pruébalo$\PageIndex{22}$

Bill quería probar diferentes embarcaciones acuáticas. Se fue 62 millas río abajo en una lancha a motor y 27 millas río abajo en una moto acuática. Su velocidad en la moto acuática era 10 mph más rápida que en la lancha motora. Bill pasó un total de 4 horas en el agua. ¿Cuál era su tasa de velocidad en la lancha motora?

Contestar: 20 mph

Ejercicio$\PageIndex{23}$

Nancy tomó un viaje de 3 horas. Se fue 50 millas antes de quedar atrapada en una tormenta. Entonces manejó 68 millas a 9 mph menos de lo que había conducido cuando hacía buen tiempo. ¿Cuál era su velocidad conduciendo en la tormenta?

Pruébalo$\PageIndex{24}$

Chester montó su bicicleta cuesta arriba 24 millas y luego regresó cuesta abajo a 2 mph más rápido que su cuesta arriba. Si le tomó 2 horas más andar cuesta arriba que cuesta abajo, l, ¿cuál era su tarifa cuesta arriba?

Contestar: 4 mph

Ejercicio$\PageIndex{25}$

Matthew corrió a la casa de su amigo a 12 millas de distancia y luego se llevó de regreso a casa. Le tomó 2 horas más trotar ahí que regresar. Su tasa de trote era 25 mph más lenta que la velocidad cuando estaba montando. ¿Cuál era su tasa de jogging?

Pruébalo$\PageIndex{26}$

Hudson recorre 1080 millas en un jet y luego 240 millas en automóvil para llegar a una reunión de negocios. El jet va 300 mph más rápido que la velocidad del automóvil, y el viaje en automóvil dura 1 hora más que el jet. ¿Cuál es la velocidad del auto?

Contestar: 60 mph

Ejercicio$\PageIndex{27}$

Nathan caminó por una vía asfáltica por 12 millas. Caminó las 12 millas de regreso a su auto en un camino de grava a través del bosque. Sobre el asfalto caminó 2 millas por hora más rápido que sobre la grava. El paseo sobre la grava tardó una hora más que el paseo sobre el asfalto. ¿Qué tan rápido caminó sobre la grava?

Pruébalo$\PageIndex{28}$

John puede volar su avión 2800 millas con una velocidad del viento de 50 mph al mismo tiempo que puede viajar 2400 millas contra el viento. Si la velocidad del viento es de 50 mph, encuentra la velocidad de su avión.

Contestar: 650 mph

Ejercicio$\PageIndex{29}$

La lancha rápida de Jim puede viajar 20 millas río arriba contra una corriente de 3 mph en la misma cantidad de tiempo que viaja 22 millas aguas abajo con una velocidad de corriente de 3 mph. Encuentra la velocidad del bote Jim.

Pruébalo$\PageIndex{30}$

Hazel necesita llegar a la casa de su nieta tomando un avión y un auto de alquiler. Viaja 900 millas en avión y 250 millas en auto. El avión viaja 250 mph más rápido que el auto. Si conduce el auto de alquiler por 2 horas más de lo que viajó en el avión, encuentre la velocidad del auto.

Contestar: 50 mph

Ejercicio$\PageIndex{31}$

Stu entrenó durante 3 horas ayer. Corrió 14 millas y luego viajó en bicicleta 40 millas. Su velocidad de ciclismo es 6 mph más rápida que su velocidad de carrera. ¿Cuál es su velocidad de carrera?

Pruébalo$\PageIndex{32}$

Al conducir el viaje de 9 horas a casa, Sharon condujo 390 millas en la interestatal y 150 millas en carreteras rurales. Su velocidad en la interestatal era 15 más que en las carreteras rurales. ¿Cuál era su velocidad en las carreteras rurales?

Contestar: 50 mph

Ejercicio$\PageIndex{33}$

A dos hermanas les gusta competir en sus paseos en bicicleta. Tamara puede ir 4 mph más rápido que su hermana, Samantha. Si Samantha tarda 1 hora más que Tamara en recorrer 80 millas, ¿qué tan rápido puede Samantha andar en bicicleta?

Resolver aplicaciones de trabajo

En los siguientes ejercicios, resolver aplicaciones de trabajo.

Pruébalo$\PageIndex{34}$

Mike, un albañil experimentado, puede construir una pared en 3 horas, mientras que su hijo, que está aprendiendo, puede hacer el trabajo en 6 horas. ¿Cuánto tiempo les toma construir un muro juntos?

Contestar: 2 horas

Ejercicio$\PageIndex{35}$

Sam tarda 4 horas en rastrillar el césped delantero mientras su hermano, Dave, puede rastrillar el césped en 2 horas. ¿Cuánto tiempo les llevará rastrillar el césped trabajando juntos?

Pruébalo$\PageIndex{36}$

Mary puede limpiar su departamento en 6 horas mientras que su compañera de cuarto puede limpiar el departamento en 5 horas. Si trabajan juntos, ¿cuánto tiempo les llevaría limpiar el departamento?

Contestar: 2 horas y 44 minutos

Ejercicio$\PageIndex{37}$

Brian puede colocar una losa de concreto en 6 horas, mientras que Greg puede hacerlo en 4 horas. Si Brian y Greg trabajan juntos, ¿cuánto tiempo tomará?

Pruébalo$\PageIndex{38}$

Leeson puede reescribir una copia de periódico en 4 horas. Si Ryan ayuda, pueden hacer el trabajo en 3 horas. ¿Cuánto tiempo le tomaría a Ryan hacer su trabajo solo?

Contestar: 12 horas

Ejercicio$\PageIndex{39}$

Paul puede limpiar el piso de un aula en 3 horas. Cuando su asistente le ayuda, el trabajo toma 2 horas. ¿Cuánto tiempo tardaría el asistente en hacerlo solo?

Pruébalo$\PageIndex{40}$

Josephine puede corregir los exámenes de sus alumnos en 5 horas, pero si la asistente de su maestra ayuda, les tomaría 3 horas. ¿Cuánto tiempo tardaría el asistente en hacerlo solo?

Contestar: 7 horas y 30 minutos

Ejercicio$\PageIndex{41}$

Lavando el auto de su papá solo, Levi de ocho años tarda 2.5 horas y medio. Si su papá le ayuda, entonces toma 1 hora. ¿Cuánto tiempo le toma al papá de Levi's lavar el auto solo?

Pruébalo$\PageIndex{42}$

Jackson puede quitar las tejas de una casa en 7 horas, mientras que Martin puede quitarse las tejas en 5 horas. ¿Cuánto tiempo les llevará quitarse las tejas si trabajan juntas?

Contestar: 2 horas y 55 minutos

Ejercicio$\PageIndex{43}$

Al final del día Dodie puede limpiar su peluquería en 15 minutos. Ann, que trabaja con ella, puede limpiar el salón en 30 minutos. ¿Cuánto tiempo les llevaría limpiar la tienda si trabajan juntos?

Pruébalo$\PageIndex{44}$

Ronald puede palear el camino de entrada en 4 horas, pero si su hermano Donald ayuda tardaría 2 horas. ¿Cuánto tiempo le tomaría a Donald palear el camino de entrada solo?

Contestar: 4 horas

Ejercicio$\PageIndex{45}$

Tina tarda 3 horas en congelar sus galletas navideñas, pero si Candy la ayuda le lleva 2 horas. ¿Cuánto tiempo tardaría a Candy en congelar las galletas navideñas sola?

Matemáticas cotidianas

Pruébalo$\PageIndex{46}$

A Dana le gusta llevar a su perro a pasear, pero a veces su perro se escapa y tiene que correr tras él. Dana caminó a su perro por 7 millas pero luego tuvo que correr 1 milla, pasando un tiempo total de 2.5 horas con su perro. Su velocidad de carrera era 3 mph más rápida que su velocidad de caminar. Encuentra su velocidad de caminar.

Contestar: 3 mph

Ejercicio$\PageIndex{47}$

Ken y Joe salen de su departamento para ir a un partido de fútbol a 45 millas de distancia. Ken conduce su auto 30 mph más rápido Joe puede andar en bicicleta. Si Joe tarda 2 horas más que Ken en llegar al juego, ¿cuál es la velocidad de Joe?

Ejercicios de escritura

Ejercicio$\PageIndex{48}$

En Ejemplo, se tachó la solución h=−4. Explique por qué.

Ejercicio$\PageIndex{49}$

Paula y Yuki son compañeras de cuarto. Paula tarda 3 horas en limpiar su departamento. Yuki tarda 4 horas en limpiar el departamento. La ecuación se$\frac{1}{3}+\frac{1}{4}=\frac{1}{t}$ puede utilizar para encontrar t, el número de horas que les tomaría a ambos, trabajando juntos, limpiar su departamento. Explique cómo esta ecuación modela la situación.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

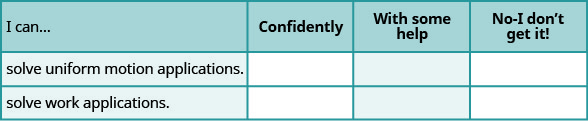
$Esta tabla tiene tres filas y cuatro columnas. La primera fila es una fila de encabezado y etiqueta cada columna. La primera columna está etiquetada como “Puedo...”, la segunda “Confiadamente”, la tercera “Con algo de ayuda” y la última “No—no lo entiendo”. En la columna “Puedo...” la siguiente fila dice “resolver aplicaciones de movimiento uniforme”. La siguiente fila dice, “resolver aplicaciones de trabajo”. Las columnas restantes están en blanco.$

ⓑ En una escala del 1—10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?