Saltar al contenido principal
LibreTexts Español

8.7: Resolver Proporción y Aplicaciones de Figuras Similares

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    110277

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje

    Al final de esta sección, podrás:

    • Resolver proporciones
    • Resolver aplicaciones de figuras similares
    Nota

    Antes de comenzar, toma este cuestionario de preparación.

    Si pierdes algún problema, vuelve a la sección listada y revisa el material.

    1. Resolver\(\dfrac{n}{3}=30\).
      Si te perdiste este problema, revisa el Ejercicio 2.2.25.
    2. El perímetro de una ventana triangular es de 23 pies. Las longitudes de dos lados son de diez pies y seis pies. ¿Cuánto dura el tercer lado?
      Si te perdiste este problema, revisa el Ejemplo 3.4.2

    Resolver proporciones

    Cuando dos expresiones racionales son iguales, la ecuación que las relaciona se llama proporción.

    Definición: PROPORCIÓN

    Una proporción es una ecuación de la forma\(\dfrac{a}{b}=\dfrac{c}{d}\), donde\(b \ne 0\),\(d \ne 0\).

    La proporción se lee “a es a b, como c es a d”

    La ecuación\(\dfrac{1}{2}=\dfrac{4}{8}\) is a proportion because the two fractions are equal.

    La proporción\(\dfrac{1}{2}=\dfrac{4}{8}\) se lee “1 es a 2 como 4 es a 8”.

    Las proporciones se utilizan en muchas aplicaciones para “escalar” cantidades. Empezaremos con un ejemplo muy sencillo para que veas cómo funcionan las proporciones. Incluso si puedes averiguar la respuesta al ejemplo de inmediato, asegúrate de aprender también a resolverlo usando proporciones.

    Supongamos que un director de escuela quiere tener 1 maestro para 20 alumnos. Podría usar proporciones para encontrar el número de profesores para 60 alumnos. Dejamos x ser el número de profesores para 60 alumnos y luego establecemos la proporción:

    \[\dfrac{1\,\text{teacher}}{20\,\text{students}}=\dfrac{x\,\text{teachers}}{60\,\text{students}}\nonumber\]

    Tenemos cuidado de igualar las unidades de los numeradores y las unidades de los denominadores: maestros en los numeradores, estudiantes en los denominadores.

    Dado que una proporción es una ecuación con expresiones racionales, resolveremos proporciones de la misma manera que resolvimos ecuaciones en Resolver ecuaciones racionales. Multiplicaremos ambos lados de la ecuación por la LCD para borrar las fracciones y luego resolver la ecuación resultante.

      .
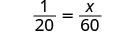    Multiplica ambos lados por la pantalla LCD, 60. .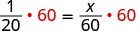
    Simplificar. .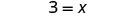
      El director necesita 3 profesores para 60 alumnos.

    Ahora vamos a hacer algunos ejemplos de resolver proporciones numéricas sin ninguna unidad. Entonces resolveremos aplicaciones usando proporciones.

    Ejemplo\(\PageIndex{1}\)

    \(\dfrac{x}{63}=\dfrac{4}{7}\).

        .
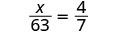    Para aislar x, multiplique ambos lados por la pantalla LCD, 63.   .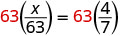
    Simplificar.   .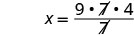
    Dividir los factores comunes.   .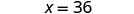
    Cheque. Para verificar nuestra respuesta, sustituimos en la proporción original.    
      .  
    . .  
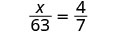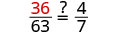    Mostrar factores comunes. .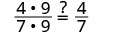  
    Simplificar. .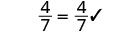  
    Pruébalo\(\PageIndex{1}\)

    \(\dfrac{n}{84}=\dfrac{11}{12}\).

    Contestar

    77

    Pruébalo\(\PageIndex{2}\)

    \(\dfrac{y}{96}=\dfrac{13}{12}\).

    Contestar

    104

    Ejemplo\(\PageIndex{2}\)

    \(\dfrac{144}{a}=\dfrac{9}{4}\).

        .
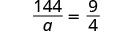    Multiplica ambos lados por la pantalla LCD.   .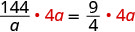
    Eliminar factores comunes en cada lado.   .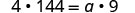
    Simplificar.   .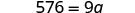
    Divide ambos lados por 9.   .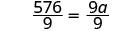
    Simplificar.   .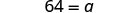
    Cheque.    
      .  
    . .  
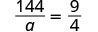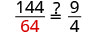    Mostrar factores comunes. .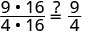  
    Simplificar. .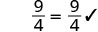  
    Pruébalo\(\PageIndex{3}\)

    \(\dfrac{91}{b}=\dfrac{7}{5}\).

    Contestar

    65

    Pruébalo\(\PageIndex{4}\)

    \(\dfrac{39}{c}=\dfrac{13}{8}\).

    Contestar

    24

    Ejemplo\(\PageIndex{3}\)

    \(\dfrac{n}{n+14}=\dfrac{5}{7}.\)

        .
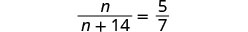    Multiplica ambos lados por la pantalla LCD.   .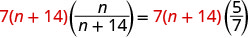
    Eliminar factores comunes en cada lado.   .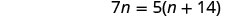
    Simplificar.   .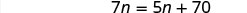
    Resolver para n.   .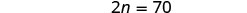
        .
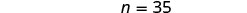    Cheque.    
      .  
    . .  
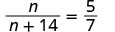    Simplificar. .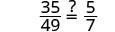  
    Mostrar factores comunes. .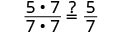  
    Simplificar. .  
    Pruébalo\(\PageIndex{5}\)

    \(\dfrac{y}{y+55}=\dfrac{3}{8}\).

    Contestar

    33

    Pruébalo\(\PageIndex{6}\)

    \(\dfrac{z}{z−84}=−\dfrac{1}{5}\).

    Contestar

    14

    Ejemplo\(\PageIndex{4}\)

    \(\dfrac{p+12}{9}=\dfrac{p−12}{6}\).

        .
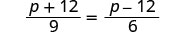    Multiplica ambos lados por la pantalla LCD, 18.   .
    Simplificar.   .
    Distribuir.   .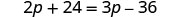
    Resolver fpr p.   .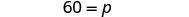
    Cheque.    
      .  
    . .  
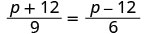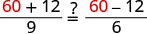    Simplificar. .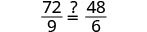  
    Dividir. .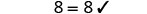  
    Pruébalo\(\PageIndex{7}\)

    \(\dfrac{v+30}{8}=\dfrac{v+66}{12}\).

    Contestar

    42

    Pruébalo\(\PageIndex{8}\)

    \(\dfrac{2x+15}{9}=\dfrac{7x+3}{15}\).

    Contestar

    6

    Para resolver aplicaciones con proporciones, seguiremos nuestra estrategia habitual para resolver aplicaciones. Pero cuando establecemos la proporción, debemos asegurarnos de tener las unidades correctas, las unidades en los numeradores deben coincidir y las unidades en los denominadores deben coincidir.

    Ejemplo\(\PageIndex{5}\)

    Cuando los pediatras recetan acetaminofén a los niños, prescriben 5 mililitros (ml) de acetaminofén por cada 25 libras del peso del niño. Si Zoe pesa 80 libras, ¿cuántos mililitros de acetaminofén le recetará su médico?

    Identificar lo que se nos pide encontrar, y elegir una variable para representarlo. ¿Cuántos ml de acetaminofén prescribirá el médico?
      Dejar a=ml de acetaminofén.
    Escribe una frase que dé la información para encontrarla. Si se recetan 5 ml por cada 25 libras, ¿cuánto se recetará por 80 libras?
    Traduzca en una proporción: tenga cuidado con las unidades.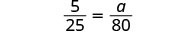

    .
    Multiplica ambos lados por la pantalla LCD, 400. .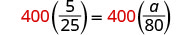
    Eliminar factores comunes en cada lado. .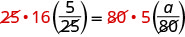
    Simplifica, pero no multipliques por la izquierda. Observe cuál será el siguiente paso. .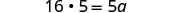
    Resolver por un. .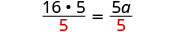
    Cheque. .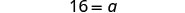
    ¿La respuesta es razonable?  
    Sí, ya que 80 es aproximadamente 3 veces 25, el medicamento debe ser aproximadamente 3 veces 5. Entonces 16 ml tiene sentido.  
    .  
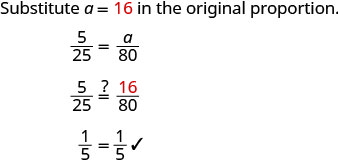    Escribe una oración completa. El pediatra le recetaría 16 ml de acetaminofén a Zoe.
    Pruébalo\(\PageIndex{9}\)

    Los pediatras prescriben 5 mililitros (ml) de acetaminofén por cada 25 libras del peso de un niño. ¿Cuántos mililitros de acetaminofén le recetará el médico a Emilia, quien pesa 60 libras?

    Contestar

    12 ml

    Pruébalo\(\PageIndex{10}\)

    Por cada 1 kilogramo (kg) de peso de un niño, los pediatras prescriben 15 miligramos (mg) de un reductor de fiebre. Si Isabella pesa 12 kg, ¿cuántos miligramos del reductor de fiebre prescribirá el pediatra?

    Contestar

    180 ml

    Ejemplo\(\PageIndex{6}\)

    Un macchiato de caramelo helado de 16 onzas tiene 230 calorías. ¿Cuántas calorías hay en un macchiato de caramelo helado de 24 onzas?

    Identificar lo que se nos pide encontrar, y elegir una variable para representarlo. ¿Cuántas calorías hay en un macchiato de caramelo helado de 24 onzas?
      Deje que c=calorías en 24 onzas.
    Escribe una frase que dé la información para encontrarla. Si hay 230 calorías en 16 onzas, entonces ¿cuántas calorías hay en 24 onzas?
    Traduzca en una proporción: tenga cuidado con las unidades.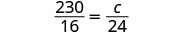

    .
    Multiplica ambos lados por la pantalla LCD, 48. .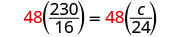
    Eliminar factores comunes en cada lado. .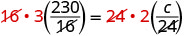
    Simplificar. .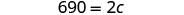
    Resolver para c. .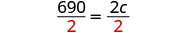
      .
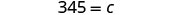    Cheque.  
    ¿La respuesta es razonable?  
    Sí, 345 calorías por 24 onzas es más de 290 calorías por 16 onzas, pero no demasiado más.  
    .  
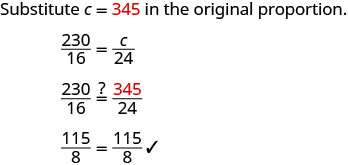    Escribe una oración completa. Hay 345 calorías en un macchiato de caramelo helado de 24 onzas.
    Pruébalo\(\PageIndex{11}\)

    En un restaurante de comida rápida, un batido de chocolate de 22 onzas tiene 850 calorías. ¿Cuántas calorías hay en su batido de chocolate de 12 onzas? Redondee su respuesta al número entero más cercano.

    Contestar

    464 calorías

    Pruébalo\(\PageIndex{12}\)

    A Yaneli le encantan los caramelos Starburst, pero quiere mantener sus refrigerios a 100 calorías. Si los caramelos tienen 160 calorías por 8 piezas, ¿cuántas piezas puede tener en su merienda?

    Contestar

    5 piezas

    Ejemplo\(\PageIndex{7}\)

    Josías se fue a México para las vacaciones de primavera y cambió 325 dólares en pesos mexicanos. En ese momento, el tipo de cambio tenía $1 US es igual a 12.54 pesos mexicanos. ¿Cuántos pesos mexicanos obtuvo para su viaje?

    ¿Qué se le pide que encuentre? ¿Cuántos pesos mexicanos obtuvo Josías?
    Asignar una variable. Let p=el numero de pesos mexicanos.
    Escribe una frase que dé la información para encontrarla. Si $1 US es igual a 12.54 pesos mexicanos, entonces $325 es ¿cuántos pesos?

    Traduzca en una proporción: tenga cuidado con las unidades.

    .
    Multiplica ambos lados por la pantalla LCD, 12.54p. .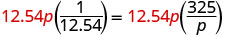
    Eliminar factores comunes en cada lado. .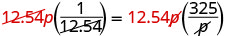
    Simplificar. .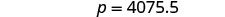
    Cheque.  
    ¿La respuesta es razonable?  
    Sí, $100 serían 1,254 pesos. $325 es un poco más de 3 veces esta cantidad, así que nuestra respuesta de 4075.5 pesos tiene sentido.  
    .  
    Escribe una oración completa. Josiah consiguió 4075.5 pesos por su viaje de vacaciones de primavera.
    Pruébalo\(\PageIndex{13}\)

    Yurianna va a Europa y quiere cambiar 800 dólares en euros. Al tipo de cambio actual, $1 US es igual a 0.738 Euro. ¿Cuántos euros tendrá para su viaje?

    Contestar

    590.4 Euros

    Pruébalo\(\PageIndex{14}\)

    Corey y Nicole viajan a Japón y necesitan cambiar 600 dólares por yenes japoneses. Si cada dólar es 94.1 yenes, ¿cuántos yenes obtendrán?

    Contestar

    56,460 yenes

    En el ejemplo anterior, relacionamos el número de pesos con el número de dólares usando una proporción. Podríamos decir que el número de pesos es proporcional al número de dólares. Si dos cantidades están relacionadas por una proporción, decimos que son proporcionales.

    Resolver aplicaciones de figuras similares

    Cuando encoges o agrandas una foto en un teléfono o tableta, averiguas una distancia en un mapa, o usas un patrón para construir una estantería o coser un vestido, estás trabajando con figuras similares. Si dos figuras tienen exactamente la misma forma, pero diferentes tamaños, se dice que son similares. Uno es un modelo a escala del otro. Todos sus ángulos correspondientes tienen las mismas medidas y sus lados correspondientes están en la misma proporción.

    Definición: Cifras similares

    Dos cifras son similares si las medidas de sus ángulos correspondientes son iguales y sus lados correspondientes están en la misma proporción.

    Por ejemplo, los dos triángulos de la Figura son similares. Cada lado de ΔABC es 4 veces la longitud del lado correspondiente de ΔXYZ.

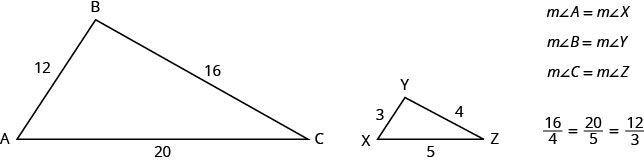
    En la imagen anterior se muestran los pasos para resolver la proporción 1 dividida por 12.54 equivale a 325 dividida por p. ¿Qué se le pide encontrar? ¿Cuántos pesos mexicanos obtuvo? Asignar una variable. Que p sea igual al número de pesos. Escribe una frase que dé la información para encontrarla. Si un dólar US es igual a 12.54 pesos, entonces 325 dólares es cuántos pesos. Traduzca en una proporción, tenga cuidado con las unidades. Dólares pesos divididos equivale a dólares divididos por pesos para obtener 1 dividido por 12.54 equivale a 325 dividido por p. Multiplicar ambos lados por la LCD, 12.54 p para obtener 1 dividido por 12.54 p por 1 dividido por 12.54 es igual a 12.54 p por 325 dividido por p. Eliminar factores comunes de ambos lados. Tacha 12.54 del lado izquierdo de la ecuación. Tachar p del lado derecho de la ecuación. Simplifica para obtener p es igual a 4075.5 en la proporción original. Cheque. ¿La respuesta es razonable? Sí, $100 serían $1254 pesos. $325 es un poco más de 3 veces esta cantidad, así que nuestra respuesta de 4075.5 pesos tiene sentido. Sustituto p equivale a 4075.5 en la proporción original. Usa una calculadora. Ahora tenemos 1 dividido por 12.54 es igual a 325 dividido por p. siguiente, 1 dividido por 12.54 es igual a 325 dividido por 4075.5 para obtener 0.07874 es igual a 0.07874. La respuesta comprueba.

    Esto se resume en la Propiedad de Triángulos Similares.

    Definición: PROPIEDAD DE TRIANGULOS SIMIL

    Si ΔABC es similar a ΔXYZ

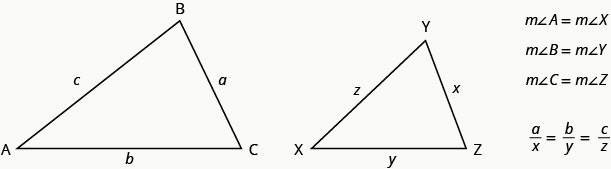
    La figura anterior muestra triángulos similares. El triángulo más grande etiquetado A B C. La longitud de A a B es c, La longitud de B a C es a. La longitud de C a A es b. El triángulo más grande está etiquetado X Y Z. La longitud de X a Y es z. La longitud de Y a Z es x. La longitud de X a Z es y. A la derecha de los triángulos, indica esa medida del ángulo correspondiente A es igual a la medida del ángulo correspondiente X, la medida del ángulo correspondiente B es igual a la medida del ángulo correspondiente Y, y la medida del ángulo correspondiente C es igual a la medida del ángulo correspondiente Z. Por lo tanto, a dividido por x es igual a b dividido por y es igual a c dividido por z.

    Para resolver aplicaciones con cifras similares seguiremos la Estrategia de Resolución de Problemas para Aplicaciones Geométricas que usamos anteriormente.

    Definición: SOLUCIONAR APLICACIONES DE GEOM
    1. Lee el problema y haz que se entiendan todas las palabras e ideas. Dibuja la figura y etiquétala con la información dada.
    2. Identificar lo que estamos buscando.
    3. Nombra lo que estamos buscando eligiendo una variable para representarlo.
    4. Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
    5. Resolver la ecuación usando buenas técnicas de álgebra.
    6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
    7. Contesta la pregunta con una oración completa.
    Ejemplo\(\PageIndex{8}\)

    ΔABC es similar a ΔXYZ

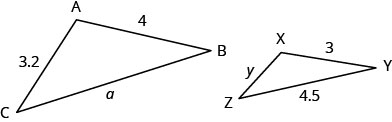
    La imagen de arriba muestra dos triángulos similares. Se dan dos lados para cada triángulo. El triángulo más grande está etiquetado como A B C. La longitud de A a B es 4. La longitud de B a C es a. La longitud de C a A es 3.2. El triángulo más pequeño está etiquetado X Y Z. La longitud de X a Y es 3. La longitud de Y a Z es 4.5. La longitud de Z a X es y.

    Paso 1. Lee el problema. Dibuja la figura y etiquétala con la información dada. Se da la figura.
    Paso 2. Identificar lo que estamos buscando. la longitud de los lados de triángulos similares.
    Paso 3. Nombra las variables.

    Dejar a= longitud del tercer lado de ΔABC.

    y= longitud del tercer lado de ΔXYZ.
    Paso 4. Traducir. Dado que los triángulos son similares, los lados correspondientes son proporcionales.
    Necesitamos escribir una ecuación que compare el lado que estamos buscando con una relación conocida. Ya que el lado AB = 4 corresponde al lado XY = 3 sabemos\(\dfrac{AB}{XY}=\dfrac{4}{3}\). Entonces escribimos ecuaciones con\(\dfrac{AB}{XY}\) para encontrar los lados que estamos buscando. Tenga cuidado de hacer coincidir correctamente los lados correspondientes. \(\dfrac{AB}{XY}=\dfrac{BC}{YZ}=\dfrac{AC}{XZ}\).
    .
    Sustituto. ..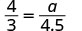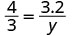
    Paso 5. Resuelve la ecuación.
    .
    Figure_08_07_030f_img_new.jpg "/>
      ..
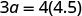
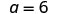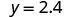    Paso 6. Cheque.
    Paso 7. Contesta la pregunta. El tercer lado de ΔABC es 6 y el tercer lado de ΔXYZ es 2.4.
    Pruébalo\(\PageIndex{15}\)

    ΔABC es similar a ΔXYZ. Las longitudes de dos lados de cada triángulo se dan en la figura.

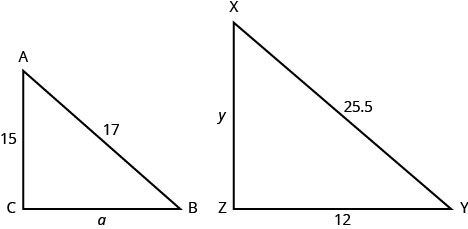
    La imagen de arriba muestra dos triángulos similares. El triángulo más pequeño está etiquetado como A B C. La longitud de dos lados se da para el triángulo más pequeño A B C. La longitud de A a B es 17. La longitud de B a C es a. La longitud de C a D es de 15. El triángulo más grande está etiquetado X Y Z. La longitud se da para dos lados. La longitud de X a Y es de 25.5. La longitud de Y a Z es 12. La longitud de Z a X es y.

    Encuentra la longitud del lado a

    Contestar

    8

    Pruébalo\(\PageIndex{16}\)

    ΔABC es similar a ΔXYZ. Las longitudes de dos lados de cada triángulo se dan en la figura.

    Contestar

    22.5

    El siguiente ejemplo muestra cómo se utilizan triángulos similares con los mapas.

    Ejemplo\(\PageIndex{9}\)

    En un mapa, San Francisco, Las Vegas y Los Ángeles forman un triángulo cuyos lados se muestran en la siguiente figura. Si la distancia real de Los Ángeles a Las Vegas es de 270 millas, encuentre la distancia de Los Ángeles a San Francisco.

    La imagen de arriba muestra dos triángulos similares y cómo se utilizan con los mapas. El triángulo más pequeño de la izquierda muestra a San Francisco, Las Vegas y Los Ángeles en los tres puntos. De San Francisco a Los Ángeles es de 1.3 pulgadas. De Los Ángeles a Las Vegas es de 1 pulgada. Las Vegas a San Francisco es de 2.1 pulgadas. El segundo triángulo más grande muestra los mismos puntos. La distancia de San Francisco a Los Ángeles es x. La distancia de Los Ángeles a Las Vegas es de 270 millas. No se nota la distancia de Las Vegas a San Francisco.

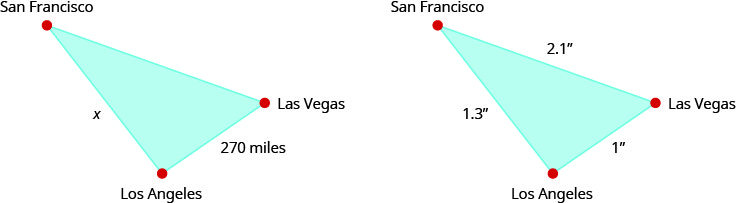
    Lee el problema. Dibuja las figuras y etiqueta con la información dada. Las cifras se muestran arriba.
    Identificar lo que estamos buscando. La distancia real de Los Ángeles a San Francisco.
    Nombra las variables. Dejar x= distancia de Los Ángeles a San Francisco.
    Traducir en una ecuación. Dado que los triángulos
    son similares, los lados correspondientes son
    proporcionales. Haremos los numeradores
    “millas” y los denominadores “pulgadas”.    		 .
      .
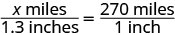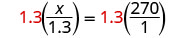    Resuelve la ecuación. .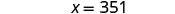
    Cheque.  
    En el mapa, la distancia de Los Ángeles a
    San Francisco es más que la distancia de
    Los Ángeles a Las Vegas. Ya que 351 es
    más de 270 la respuesta tiene sentido.    		  
    .  
    Contesta la pregunta. La distancia de Los Ángeles a San Francisco es de 351 millas.
    PRUEBAR\(\PageIndex{17}\)

    En el mapa, Seattle, Portland y Boise forman un triángulo cuyos lados se muestran en la siguiente figura. Si la distancia real de Seattle a Boise es de 400 millas, encuentra la distancia entre Seattle y Portland.

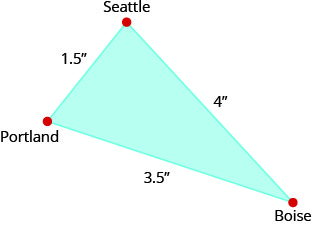
    La imagen de arriba es un triángulo con un lado etiquetado como “Seattle, 4.5 pulgadas”. El otro lado está etiquetado como “Portland 3.5 pulgadas”. El tercer lado está etiquetado 1.5 pulgadas. El vértice está etiquetado como “Boise”.

    Contestar

    150 millas

    Pruébalo\(\PageIndex{18}\)

    Usando el mapa de arriba, encuentra la distancia de Portland a Boise.

    Contestar

    350 millas

    Podemos usar figuras similares para encontrar alturas que no podemos medir directamente.

    Ejemplo\(\PageIndex{10}\)

    Tyler mide 6 pies de altura. Al final de la tarde, su sombra medía 8 pies de largo. Al mismo tiempo, la sombra de un árbol tenía 24 pies de largo. Encuentra la altura del árbol.

    Lee el problema y dibuja una figura. .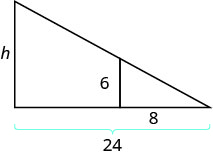
    Buscamos h, la altura del árbol.  
    Usaremos triángulos similares para escribir una ecuación.  
    El triángulo pequeño es similar al triángulo grande. .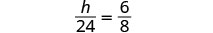
    Resolver la proporción. .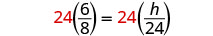
    Simplificar. .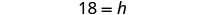
    Cheque.  

    La altura de Tyler es menor que la longitud de su sombra por lo que tiene sentido que la altura del árbol sea menor que la longitud de su sombra.

    		  
    .  
    Pruébalo\(\PageIndex{19}\)

    Un poste telefónico proyecta una sombra de 50 pies de largo. Cerca, una señal de tráfico de 8 pies de altura proyecta una sombra que mide 10 pies de largo. ¿Qué tan alto es el poste telefónico?

    Contestar

    40 pies

    Pruébalo\(\PageIndex{20}\)

    Un pino proyecta una sombra de 80 pies junto a un edificio de 30 pies de altura que proyecta una sombra de 40 pies. ¿Qué tan alto es el pino?

    Contestar

    60 pies

    Conceptos clave

    • Propiedad de Triángulos Similares
      • Si ΔABC es similar a ΔXYZ
    • Estrategia de resolución de problemas para aplicaciones de geometría
      1. Lee el problema y asegúrate de que se entiendan todas las palabras e ideas. Dibuja la figura y etiquétala con la información dada.
      2. Identificar lo que estamos buscando.
      3. Nombra lo que estamos buscando eligiendo una variable para representarlo.
      4. Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
      5. Resolver la ecuación usando buenas técnicas de álgebra.
      6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
      7. Contesta la pregunta con una oración completa.

    Glosario

    proporción
    Una proporción es una ecuación de la forma\(\dfrac{a}{b}=\dfrac{c}{d}, where \(b \ne 0\),\(d \ne 0\). La proporción se lee “a es a b c es a d”.
    cifras similares
    Dos cifras son similares si las medidas de sus ángulos correspondientes son iguales y sus lados correspondientes están en la misma proporción.

    This page titled 8.7: Resolver Proporción y Aplicaciones de Figuras Similares is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.