9.1: Simplificar y Usar Raíces Cuadradas
- Page ID
- 110183
Al final de esta sección, podrás:
- Simplifica expresiones con raíces cuadradas
- Estimar raíces cuadradas
- Raíces cuadradas aproximadas
- Simplifique las expresiones variables con raíces cuadradas
Antes de comenzar, toma este cuestionario de preparación.
- Simplifica: ⓐ\(9^2\) ⓑ\((−9)^2\) ⓒ\(−9^2\).
Si te perdiste este problema, revisa [enlace]. - Vuelta 3.846 a la centésima más cercana.
Si te perdiste este problema, revisa [enlace]. - Para cada número, identifique si es un número real o no un número real:
ⓐ\(−\sqrt{100}\) ⓑ\(\sqrt{−100}\).
Si te perdiste este problema, revisa [enlace].
Simplifique las expresiones con raíces cuadradas
Recuerda que cuando un número n se multiplica por sí mismo, lo escribimos\(n^2\) y leemos “n al cuadrado”. Por ejemplo, se\(15^2\) lee como “15 cuadrados”, y 225 se llama el cuadrado de 15, ya que\(15^2=225\).
Si\(n^2=m\), entonces m es el cuadrado de n.
A veces tendremos que mirar a la inversa la relación entre los números y sus cuadrados. Debido a que 225 es el cuadrado de 15, también podemos decir que 15 es una raíz cuadrada de 225. Un número cuyo cuadrado es m se llama raíz cuadrada de m.
Si\(n^2=m\), entonces n es una raíz cuadrada de m.
Aviso\((−15)^2=225\) also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.
Entonces, cada número positivo tiene dos raíces cuadradas, una positiva y otra negativa. ¿Y si solo quisiéramos la raíz cuadrada positiva de un número positivo? El signo radical,\(\sqrt{m}\), denota la raíz cuadrada positiva. La raíz cuadrada positiva también se llama raíz cuadrada principal.
También utilizamos el signo radical para la raíz cuadrada de cero. Porque\(0^2=0\),\(\sqrt{0}=0\). Observe que cero tiene solo una raíz cuadrada.
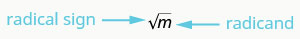
\(\sqrt{m}\)se lee como “la raíz cuadrada de m.”
Si\(m=n^2\), entonces\(\sqrt{m}=n\), para\(n \ge 0\).
La raíz cuadrada de m,\(\sqrt{m}\), es el número positivo cuyo cuadrado es m.
Ya que 15 es la raíz cuadrada positiva de 225, escribimos\(\sqrt{225}=15\). Fill in Figura para hacer una tabla de raíces cuadradas a la que pueda hacer referencia mientras trabaja este capítulo.

Sabemos que cada número positivo tiene dos raíces cuadradas y el signo radical indica el positivo. Escribimos\(\sqrt{225}=15\). Si queremos encontrar la raíz cuadrada negativa de un número, colocamos un negativo frente al signo radical. Por ejemplo,\(−\sqrt{225}=−15\).
Simplificar:
- \(\sqrt{36}\)
- \(\sqrt{196}\)
- \(−\sqrt{81}\)
- \(−\sqrt{289}\).
- Contestar
-
1.
\[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
2.
\[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
3.
\[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
4.
\[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]
Simplificar:
- \(−\sqrt{49}\)
- \(\sqrt{225}\).
- Contestar
-
- −7
- 15
implique:
- \(\sqrt{64}\)
- \(−\sqrt{121}\).
- Contestar
-
- 8
- −11
Simplificar:
- \(\sqrt{−169}\)
- \( −\sqrt{64}\)
- Contestar
-
1.
\[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]
Simplificar:
- \(\sqrt{−196}\)
- \(−\sqrt{81}\).
- Contestar
-
- no es un número real
- −9
Simplificar:
- \(−\sqrt{49}\)
- \(\sqrt{ −121}\).
- Contestar
-
- −7
- no es un número real
Al utilizar el orden de las operaciones para simplificar una expresión que tiene raíces cuadradas, tratamos al radical como un símbolo de agrupación.
Simplificar:
- \(\sqrt{25} +\sqrt{144}\)
- \(\sqrt{25+144}\).
- Contestar
-
1.
\[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]
¡Observe las diferentes respuestas en las partes 1 y 2!
Simplificar:
- \(\sqrt{9}+\sqrt{16}\)
- \(\sqrt{9+16}\).
- Contestar
-
- 7
- 5
Simplificar:
- \(\sqrt{64+225}\)
- \(\sqrt{64}+\sqrt{225}\).
- Contestar
-
- 17
- 23
Estimar raíces cuadradas
Hasta el momento sólo hemos considerado raíces cuadradas de números cuadrados perfectos. Las raíces cuadradas de otros números no son números enteros. Mira la Tabla a continuación.
| Número | Raíz cuadrada |
|---|---|
| 4 | \(\sqrt{4}=2\) |
| 5 | \(\sqrt{5}\) |
| 6 | \(\sqrt{6}\) |
| 7 | \(\sqrt{7}\) |
| 8 | \(\sqrt{8}\) |
| 9 | \(\sqrt{9}=3\) |
Las raíces cuadradas de los números entre 4 y 9 deben estar entre los dos números enteros consecutivos 2 y 3, y no son números enteros. Con base en el patrón de la tabla anterior, podríamos decir que\(\sqrt{5}\) debe estar entre 2 y 3. Usando símbolos de desigualdad, escribimos:
\(2<\sqrt{5}<3\)
Estimar\(\sqrt{60}\) entre dos números enteros consecutivos.
- Contestar
-
Piensa en los números cuadrados perfectos más cercanos al 60. Haz una mesita de estos cuadrados perfectos y sus raíces cuadradas.
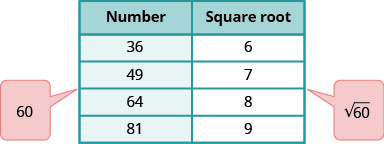
Localiza 60 entre dos cuadrados perfectos consecutivos. 
\(\sqrt{60}\)está entre sus raíces cuadradas. 
Estimar la raíz cuadrada\(\sqrt{38}\) entre dos números enteros consecutivos.
- Contestar
-
\(6<\sqrt{38}<7\)
Estimar la raíz cuadrada\(\sqrt{84}\) entre dos números enteros consecutivos.
- Contestar
-
\(9<\sqrt{84}<10\)
Raíces Cuadradas Aproximadas
Existen métodos matemáticos para aproximar raíces cuadradas, pero hoy en día la mayoría de la gente usa una calculadora para encontrarlas. Encuentra la\(\sqrt{x}\) clave en tu calculadora. Utilizarás esta clave para aproximar raíces cuadradas.
Cuando usas tu calculadora para encontrar la raíz cuadrada de un número que no es un cuadrado perfecto, la respuesta que ves no es la raíz cuadrada exacta. Es una aproximación, precisa al número de dígitos que se muestran en la pantalla de su calculadora. El símbolo para una aproximación es\(\approx\) y se lee 'aproximadamente'.
Supongamos que su calculadora tiene una pantalla de 10 dígitos. Verías que
\(\sqrt{5} \approx 2.236067978\)
Si quisiéramos redondear\(\sqrt{5}\) a dos decimales, diríamos
\(\sqrt{5} \approx 2.24\)
¿Cómo sabemos que estos valores son aproximaciones y no los valores exactos? Mira lo que sucede cuando los cuadramos:
\[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]
Sus cuadrados están cerca de 5, pero no son exactamente iguales a 5.
Usando la tecla raíz cuadrada en una calculadora y luego redondeando a dos decimales, podemos encontrar:
\[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]
Redondear\(\sqrt{17}\) a dos decimales.
- Contestar
-
\[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]
Redondear\(\sqrt{11}\) a dos decimales.
- Responder
-
\(\approx 3.32\)
Redondear\(\sqrt{13}\) a dos decimales.
- Responder
-
\(\approx 3.61\)
Simplifique las expresiones variables con raíces cuadradas
¿Y si tenemos que encontrar una raíz cuadrada de una expresión con una variable? Considerar\(\sqrt{9x^2}\). ¿Se te ocurre una expresión cuya plaza es\(9x^2\)?
\[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]
Cuando usamos el signo radical para tomar la raíz cuadrada de una expresión variable, debemos especificar que x≥0x≥0 para asegurarnos de que obtenemos la raíz cuadrada principal.
Sin embargo, en este capítulo vamos a suponer que cada variable en una expresión de raíz cuadrada representa un número no negativo y así no escribiremos\(x \ge 0\) junto a cada radical.
¿Qué pasa con las raíces cuadradas de las potencias superiores de las variables? Piense en la propiedad de poder de los exponentes que usamos en el Capítulo 6.
\((a^m)^n=a^{m·n}\)
Si cuadramos\(a^m\), el exponente se convertirá en 2m.
\((a^m)^2=a^{2m}\)
¿Cómo nos ayuda esto a tomar raíces cuadradas? Veamos algunos:
\[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]
Simplificar:
- \(\sqrt{x^6}\)
- \(\sqrt{y^{16}}\)
- Responder
-
1.
\[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]
2.\[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]
Simplificar:
- \(\sqrt{y^8}\)
- \(\sqrt{z^{12}}\).
- Responder
-
- \(y^4\)
- \(z^6\)
Simplificar:
- \(\sqrt{m^4}\)
- \(\sqrt{b^{10}}\).
- Responder
-
- \(m^2\)
- \(b^5\)
Simplificar:\(\sqrt{16n^2}\)
- Responder
-
\[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]
Simplificar:\(\sqrt{64x^2}\).
- Responder
-
\(8x\)
Simplificar:\(\sqrt{169y^2}\).
- Responder
-
\(13y\)
Simplificar:\(−\sqrt{81c^2}\).
- Responder
-
\[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]
Simplificar:\(−\sqrt{121y^2}\).
- Responder
-
\(−11y\)
Simplificar:\(−\sqrt{100p^2}\).
- Responder
-
\(−10p\)
Simplificar:\(\sqrt{36x^{2}y^{2}}\).
- Responder
-
\[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]
Simplificar:\(\sqrt{100a^{2}b^{2}}\).
- Responder
-
10ab
Simplificar:\(\sqrt{225m^{2}n^{2}}\).
- Responder
-
15mn
Simplificar:\(\sqrt{64p^{64}}\).
- Responder
-
\[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]
Simplificar:\(\sqrt{49x^{30}}\).
- Responder
-
\(7x^{15}\)
Simplificar:\(\sqrt{81w^{36}}\)
- Responder
-
\(9w^{18}\)
Simplificar:\(\sqrt{121a^{6}b^{8}}\)
- Responder
-
\[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]
Simplificar:\(\sqrt{169x^{10}y^{14}}\)
- Responder
-
\(13x^{5}y^{7}\)
Simplificar:\(\sqrt{144p^{12}q^{20}}\)
- Responder
-
\(\sqrt{12p^{6}q^{10}}\)
Acceda a este recurso en línea para obtener instrucción adicional y práctica con raíces cuadradas.
- Raíces Cuadradas
Conceptos clave
- Tenga en cuenta que la raíz cuadrada de un número negativo no es un número real.
- Cada número positivo tiene dos raíces cuadradas, una positiva y otra negativa. La raíz cuadrada positiva de un número positivo es la raíz cuadrada principal.
- Podemos estimar raíces cuadradas usando cuadrados perfectos cercanos.
- Podemos aproximar raíces cuadradas usando una calculadora.
- Cuando usamos el signo radical para tomar la raíz cuadrada de una expresión variable, debemos especificarlo\(x \ge 0\) para asegurarnos de que obtenemos la raíz cuadrada principal.
Glosario
- cuadrado de un número
-
- Si\(n^2=m\), entonces m es el cuadrado de n
- raíz cuadrada de un número
-
- Si\(n^2=m\), entonces n es una raíz cuadrada de m
- notación de raíz cuadrada
-
- Si\(m=n^2\), entonces\(\sqrt{m}=n\). Leemos\(\sqrt{m}\) como 'la raíz cuadrada de m. '


