9.4E: Ejercicios
- Page ID
- 110167
La práctica hace la perfección
Multiplicar raíces cuadradas
En los siguientes ejercicios, simplifique.
- \(\sqrt{2}·\sqrt{8}\)
- \((3\sqrt{3})(2\sqrt{18})\)
- Contestar
-
- \(44\)
- \(18\sqrt{6}\)
- \(\sqrt{6}·\sqrt{6}\)
- \((3\sqrt{2})(2\sqrt{32})\)
- \(\sqrt{7}·\sqrt{14}\)
- \((4\sqrt{8})(5\sqrt{8})\)
- Contestar
-
- \(7\sqrt{2}\)
- 160
- \(\sqrt{6}·\sqrt{12}\)
- \((2\sqrt{5})(2\sqrt{10})\)
\((5\sqrt{2})(3\sqrt{6})\)
- Contestar
-
\(30\sqrt{3}\)
\((2\sqrt{3})(4\sqrt{6})\)
\((−2\sqrt{3})(3\sqrt{18})\)
- Contestar
-
\(−18\sqrt{6}\)
\((−4\sqrt{5})(5\sqrt{10})\)
\((5\sqrt{6})(−\sqrt{12})\)
- Contestar
-
\(−30\sqrt{2}\)
\((6\sqrt{2})(−\sqrt{10})\)
\((−2\sqrt{7})(−2\sqrt{14})\)
- Contestar
-
\(28\sqrt{2}\)
\((−2\sqrt{11})(−4\sqrt{22})\)
- \((\sqrt{15y})(\sqrt{5y^3})\)
- \((\sqrt{2n^2})(\sqrt{18n^3})\)
- Contestar
-
- \(5y^2\sqrt{3}\)
- \(6n^2\sqrt{n}\)
- \((\sqrt{14x^3})(\sqrt{7x^3})\)
- \((\sqrt{3q^2})(\sqrt{48q^3})\)
- \((\sqrt{16y^2})(\sqrt{8y^4})\)
- \((\sqrt{11s^6})(\sqrt{11s})\)
- Contestar
-
- \(8y^3\sqrt{2}\)
- \(11s^3\sqrt{s}\)
ⓐ\((\sqrt{8x^3})(\sqrt{3x})\)
ⓑ\((\sqrt{7r})(\sqrt{7r^8})\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
- Contestar
-
\(40b^2\sqrt{3}\)
\((\sqrt{38c^5})(\sqrt{26c^3})\)
\((6\sqrt{3d^3})(4\sqrt{12d^5})\)
- Contestar
-
\(144d^4\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
\((2\sqrt{5d^6})(3\sqrt{20d^2})\)
- Contestar
-
\(60d^4\)
\((−2\sqrt{7z^3})(3\sqrt{14z^8})\)
\((4\sqrt{2k^5})(−3\sqrt{32k^6})\)
- Contestar
-
\(−96k^5\sqrt{k}\)
- \((\sqrt{7})^2\)
- \((−\sqrt{15})^2\)
- \((\sqrt{11})^2\)
- \((−\sqrt{21})^2\)
- Contestar
-
- 11
- 21
- \((\sqrt{19})^2\)
- \((−\sqrt{5})^2\)
- \((\sqrt{23})^2\)
- \((−\sqrt{3})^2\)
- Contestar
-
- 23
- 3
- \((4\sqrt{11})(−3\sqrt{11})\)
- \((5\sqrt{3})^2\)
- \((2\sqrt{13})(−9\sqrt{13})\)
- \((6\sqrt{5})^2\)
- Contestar
-
- −234
- 180
- \((−3\sqrt{12})(−2\sqrt{6})\)
- \( (−4\sqrt{10})^2\)
- \((−7\sqrt{5})(−3\sqrt{10})\)
- \( (−2\sqrt{14})^2\)
- Contestar
-
- \(105\sqrt{2}\)
- 56
Usa Multiplicación Polinomial para Multiplicar Raíces Cuadradas
En los siguientes ejercicios, simplifique.
- \(3(4−\sqrt{3})\)
- \(\sqrt{2}(4−\sqrt{6})\)
- \(4(6−\sqrt{11})\)
- \(\sqrt{2}(5−\sqrt{12})\)
- Contestar
-
- \(24−4\sqrt{11}\)
- \(5\sqrt{2}−2\sqrt{6}\)
- \(5(3−\sqrt{7})\)
- \(\sqrt{3}(4−\sqrt{15})\)
- \(7(−2−\sqrt{11})\)
- \(\sqrt{7}(6−\sqrt{14})\)
- Contestar
-
- \(−14−7\sqrt{11}\)
- \(6\sqrt{7}−7\sqrt{2}\)
- \(\sqrt{7}(5+2\sqrt{7})\)
- \(\sqrt{5}(\sqrt{10}+\sqrt{18})\)
- \(\sqrt{11}(8+4\sqrt{11})\)
- \(\sqrt{3}(\sqrt{12}+\sqrt{27})\)
- Contestar
-
- \(44+8\sqrt{11}\)
- 15
- \(\sqrt{11}(−3+4\sqrt{1})\)
- \(\sqrt{3}(\sqrt{15}−\sqrt{18})\)
- \(\sqrt{2}(−5+9\sqrt{2})\)
- \(\sqrt{7}(\sqrt{3}−\sqrt{21})\)
- Contestar
-
- \(18−5\sqrt{2}\)
- \(\sqrt{21}−7\sqrt{3}\)
\((8+\sqrt{3})(2−\sqrt{3})\)
\((7+\sqrt{3})(9−\sqrt{3})\)
- Contestar
-
\(60+2\sqrt{3}\)
\((8−\sqrt{2})(3+\sqrt{2})\)
\((9−\sqrt{2})(6+\sqrt{2})\)
- Contestar
-
\(52+3\sqrt{2}\)
\((3−\sqrt{7})(5−\sqrt{7})\)
\((5−\sqrt{7})(4−\sqrt{7})\)
- Contestar
-
\(27−9\sqrt{7}\)
\((1+3\sqrt{10})(5−2\sqrt{10})\)
\((7−2\sqrt{5})(4+9\sqrt{5})\)
- Contestar
-
\(−62+55\sqrt{5}\)
\((\sqrt{3}+\sqrt{10})(\sqrt{3}+2\sqrt{10})\)
\((\sqrt{11}+\sqrt{5})(\sqrt{11}+6\sqrt{5})\)
- Contestar
-
\(41+7\sqrt{55}\)
\((2\sqrt{7}−5\sqrt{11})(4\sqrt{7}+9\sqrt{11})\)
\((4\sqrt{6}+7\sqrt{13})(8\sqrt{6}−3\sqrt{13})\)
- Contestar
-
\(−81+44\sqrt{78}\)
\((5−\sqrt{u})(3+\sqrt{u})\)
\((9−\sqrt{w})(2+\sqrt{w})\)
- Contestar
-
\(18+7\sqrt{w}\)
\((7+2\sqrt{m})(4+9\sqrt{m})\)
\((6+5\sqrt{n})(11+3\sqrt{n})\)
- Contestar
-
\(66+73\sqrt{n}+15n\)
- \((3+\sqrt{5})^2\)
- \((2−5\sqrt{3})^2\)
- \((4+\sqrt{11})^2\)
- \((3−2\sqrt{5})^2\)
- Contestar
-
- \(27+8\sqrt{11}\)
- \(29−12\sqrt{5}\)
- \((9−\sqrt{6})^2\)
- \((10+3\sqrt{7})^2\)
- \((5−\sqrt{10})^2\)
- \((8+3\sqrt{2})^2\)
- Contestar
-
- \(35−10\sqrt{10}\)
- \(82+48\sqrt{2}\)
\((3−\sqrt{5})(3+\sqrt{5})\)
\((10−\sqrt{3})(10+\sqrt{3})\)
- Contestar
-
97
\((4+\sqrt{2})(4−\sqrt{2})\)
\((7+\sqrt{10})(7−\sqrt{10})\)
- Contestar
-
39
\((4+9\sqrt{3})(4−9\sqrt{3})\)
\((1+8\sqrt{2})(1−8\sqrt{2})\)
- Contestar
-
−127
\((12−5\sqrt{5})(12+5\sqrt{5})\)
\((9−4\sqrt{3})(9+4\sqrt{3})\)
- Contestar
-
33
Práctica Mixta
En los siguientes ejercicios, simplifique.
\(\sqrt{3}·\sqrt{21}\)
\((4\sqrt{6})(−\sqrt{18})\)
- Contestar
-
\(−24\sqrt{3}\)
\((−5+\sqrt{7})(6+\sqrt{21})\)
\((−5\sqrt{7})(6\sqrt{21})\)
- Contestar
-
\(−210\sqrt{3}\)
\((−4\sqrt{2})(2\sqrt{18})\)
\((\sqrt{35y^3})(\sqrt{7y^3})\)
- Contestar
-
\(7y^3\sqrt{5}\)
\((4\sqrt{12x^5})(2\sqrt{6x^3})\)
\((\sqrt{29})^2\)
- Contestar
-
29
\((−4\sqrt{17})(−3\sqrt{17})\)
\((−4+\sqrt{17})(−3+\sqrt{17})\)
- Contestar
-
\(29−7\sqrt{17}\)
Matemáticas cotidianas
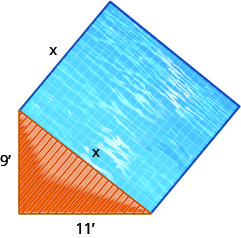
Un paisajista quiere poner una alberca reflectante cuadrada junto a una cubierta triangular, como se muestra a continuación. La cubierta triangular es un triángulo rectángulo, con patas de longitud 9 pies y 11 pies, y la piscina estará adyacente a la hipotenusa.
- Usa el Teorema de Pitágoras para encontrar la longitud de un lado de la piscina. Redondee su respuesta a la décima de pie más cercana.
- Encuentra el área exacta de la piscina.
Un artista quiere hacer un pequeño monumento en forma de base cuadrada rematada por un triángulo rectángulo, como se muestra a continuación. La base cuadrada será adyacente a una pata del triángulo. La otra pata del triángulo medirá 2 pies y la hipotenusa será de 5 pies.
- Usa el Teorema de Pitágoras para encontrar la longitud de un lado de la base cuadrada. Redondee su respuesta a la décima de pie más cercana.
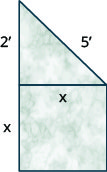
- Encuentra el área exacta de la cara de la base cuadrada.
- Contestar
-
- 4.6pies
- 21 pies cuadrados
Se realizará un jardín cuadrado con un borde de piedra en un borde. Si solo hay\(3+\sqrt{10}\) pies de piedra disponibles, simplifique\((3+\sqrt{10})^2\) para determinar el área del jardín más grande de este tipo.
Se hará un jardín de manera que contenga dos secciones cuadradas, una sección con\(\sqrt{5}+\sqrt{6}\) yardas de longitud lateral y una sección con\(\sqrt{2}+\sqrt{3}\) yardas de longitud lateral. \((\sqrt{5}+\sqrt{6})(\sqrt{2}+\sqrt{3})\)Simplificar para determinar el área total del jardín.
Supongamos que en el ejercicio anterior se agregará una tercera sección al jardín. La tercera sección es tener un ancho de\(\sqrt{432}\) pies. Escribir una expresión que dé la superficie total del jardín.
Ejercicios de escritura
- \((−\sqrt{n})^2\)Explique por qué siempre es positivo, para\(n \ge 0\).
- \(−(\sqrt{n})^2\)Explique por qué siempre es negativo, para\(n \ge 0\).
- Contestar
-
- al cuadrar un negativo, se convierte en un positivo
- ya que el negativo no está incluido entre paréntesis, no es cuadrado, y sigue siendo negativo
Utilice el patrón cuadrado binomial para simplificar\((3+\sqrt{2})^2\). Explica todos tus pasos.
Autocomprobación
ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.
ⓑ En una escala del 1—10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?


