10.5E: Ejercicios
- Page ID
- 110190
La práctica hace la perfección
Reconocer la Gráfica de una Ecuación Cuadrática en Dos Variables
En los siguientes ejercicios, grafica:
\(y=x^2+3\)
- Contestar
-
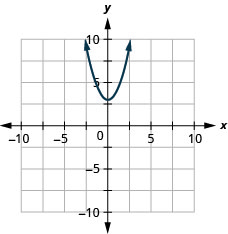
\(y=−x^2+1\)
En los siguientes ejercicios, determine si la parábola se abre hacia arriba o hacia abajo.
\(y=−2x^2−6x−7\)
- Contestar
-
abajo
\(y=6x^2+2x+3\)
y=4x^2+x−4
- Contestar
-
arriba
\(y=−9x^2−24x−16\)
Encuentra el eje de simetría y vértice de una parábola
En los siguientes ejercicios, encuentra ⓐ el eje de simetría y ⓑ el vértice.
\(y=x^2+8x−1\)
- Contestar
-
ⓐ x=−4 ⓑ (−4, −17)
\(y=x^2+10x+25\)
\(y=−x^2+2x+5\)
- Contestar
-
ⓐ x=1 ⓑ (1,6)
\(y=−2x^2−8x−3\)
Encuentra las intercepciones de una parábola
En los siguientes ejercicios, encuentra las intercepciones x - e y.
\(y=x^2+7x+6\)
- Contestar
-
y: (0,6); x: (−1,0), (−6,0)
\(y=x^2+10x−11\)
\(y=−x^2+8x−19\)
- Contestar
-
y: (0, −19); x:ninguno
\(y=x^2+6x+13\)
\(y=4x^2−20x+25\)
- Contestar
-
y: (0,25); x: (52,0)
\(y=−x^2−14x−49\)
Gráfica ecuaciones cuadráticas en dos variables
En los siguientes ejercicios, grafica usando intercepciones, el vértice y el eje de simetría.
\(y=x^2+6x+5\)
- Contestar
-
y: (0,5); x: (−1,0), (−5,0);
eje: x=−3; vértice :( −3, −4)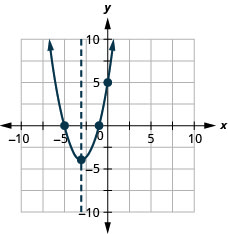
\(y=x^2+4x−12\)
\(y=x^2+4x+3\)
- Contestar
-
y: (0,3); x: (−1,0), (−3,0);
eje: x=−2; vértice :( −2, −1)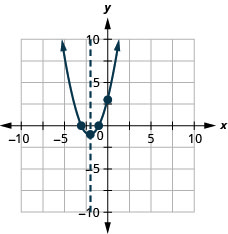
\(y=x^2−6x+8\)
\(y=9x^2+12x+4\)
- Contestar
-
y: (0,4); x:\((−\frac{2}{3},0)\);
eje:\((−\frac{2}{3}\); vértice:\((−\frac{2}{3},0)\)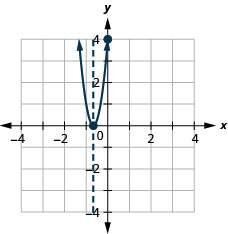
\(y=−x^2+8x−16\)
\(y=−x^2+2x−7\)
- Contestar
-
y: (0, −7); x:ninguno;
eje: x=1; vértice :( 1, −6)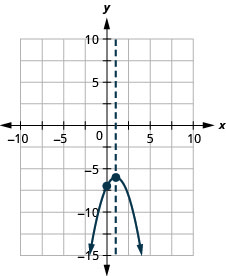
\(y=5x^2+2\)
\(y=2x^2−4x+1\)
- Contestar
-
y: (0,1); x: (1.7,0), (0.3,0);
eje: x=1; vértice :( 1, −1)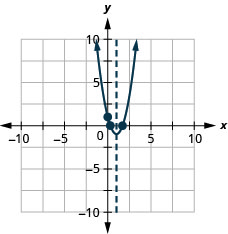
\(y=−4x^2−6x−2\)
\(y=−x^2−4x+2\)
- Contestar
-
y: (0,2); x: (−4.4,0), (0.4,0);
eje: x=−2; vértice :( −2,6)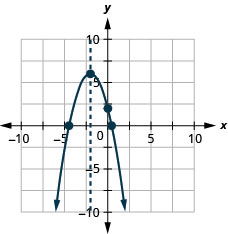
\(y=x^2+6x+8\)
\(y=5x^2−10x+8\)
- Contestar
-
y: (0,8); x:ninguno;
eje: x=1; vértice :( 1,3)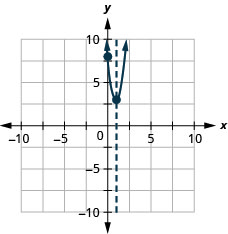
\(y=−16x^2+24x−9\)
\(y=3x^2+18x+20\)
- Contestar
-
y: (0,20); x: (−4.5,0), (−1.5,0)
eje: x=−3; vértice :( −3, −7)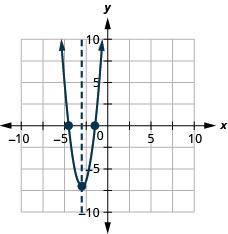
\(y=−2x^2+8x−10\)
Resolver aplicaciones máximas y mínimas
En los siguientes ejercicios, encuentra el valor máximo o mínimo.
\(y=2x^2+x−1\)
- Contestar
-
El valor mínimo es\(−\frac{9}{8}\) cuándo\(x=−\frac{1}{4}\).
\(y=−4x^2+12x−5\)
\(y=x^2−6x+15\)
- Contestar
-
El valor mínimo es 6 cuando x=3.
\(y=−x^2+4x−5\)
\(y=−9x^2+16\)
- Contestar
-
El valor máximo es 16 cuando x=0.
\(y=4x^2−49\)
En los siguientes ejercicios, resuelve. Respuestas redondas a la décima más cercana.
Una flecha se dispara verticalmente hacia arriba desde una plataforma de 45 pies de altura a una velocidad de 168 pies/seg. Usa la ecuación cuadrática\(h=−16t^2+168t+45\) para encontrar cuánto tiempo tardará la flecha en alcanzar su altura máxima, y luego encontrar la altura máxima.
- Contestar
-
En 5.3 s la flecha alcanzará una altura máxima de 486 pies.
Una piedra se lanza verticalmente hacia arriba desde una plataforma que mide 20 pies de altura a una velocidad de 160 pies/seg. Usa la ecuación cuadrática\(h=−16t^2+160t+20\) para encontrar cuánto tiempo tardará la piedra en alcanzar su altura máxima, y luego encontrar la altura máxima.
El dueño de una tienda de informática estima que al cargar x dólares cada uno por una determinada computadora, puede vender\(40−x\) computadoras cada semana. La ecuación cuadrática\(R=−x^2+40x\) se utiliza para encontrar los ingresos, R, recibidos cuando el precio de venta de una computadora es x. Encuentra el precio de venta que le dará los ingresos máximos, y luego encuentra el monto de los ingresos máximos.
- Contestar
-
20 computadoras darán el máximo de $400 en recibo.
Un minorista que vende mochilas estima que, al venderlas por x dólares cada una, podrá vender\(100−x\) mochilas al mes. La ecuación cuadrática\(R=−x^2+100x\) se utiliza para encontrar la R recibida cuando el precio de venta de una mochila es x. Encuentra el precio de venta que le dará los ingresos máximos, y luego encuentra el monto del ingreso máximo.
Un ranchero va a cercar tres lados de un corral junto a un río. Necesita maximizar el área del corral usando 240 pies de esgrima. La ecuación cuadrática A=X (240−2x) da el área del corral, A, para la longitud, x, del corral a lo largo del río. Encuentra la longitud del corral a lo largo del río que dará el área máxima, y luego encuentra el área máxima del corral.
- Contestar
-
La longitud del costado a lo largo del río del corral es de 120 pies y el área máxima es de 7,200 pies cuadrados.
Un veterinario encierra un área rectangular para correr al aire libre contra su edificio para los perros que cuida. Necesita maximizar el área usando 100 pies de esgrima. La ecuación cuadrática\(A=x(100−2x)\) da el área, A, de la carrera canina para la longitud, x, del edificio que bordeará la carrera canina. Encuentra la longitud del edificio que debe bordear la carrera canina para dar el área máxima, y luego encontrar el área máxima de la carrera canina.
Matemáticas cotidianas
En el conjunto anterior de ejercicios, se trabajó con la ecuación cuadrática\(R=−x^2+40x\) que modeló los ingresos recibidos por la venta de computadoras a un precio de x dólares. Encontraste el precio de venta que daría los ingresos máximos y calculaste los ingresos máximos. Ahora mirarás más características de este modelo.
1. Grafica la ecuación\(R=−x^2+40x\).
2. Encuentra los valores de las intercepciones x.
- Contestar
-
1.
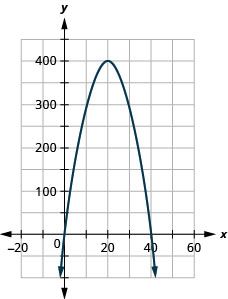
2. (0,0), (40,0)
el conjunto anterior de ejercicios, trabajaste con la ecuación cuadrática\(R=−x^2+100x\) que modeló los ingresos recibidos por vender mochilas a un precio de x dólares. Encontraste el precio de venta que daría los ingresos máximos y calculaste los ingresos máximos. Ahora mirarás más características de este modelo.
1. Grafica la ecuación\(R=−x^2+100x\).
2.Encuentra los valores de las intercepciones x.
Ejercicios de escritura
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
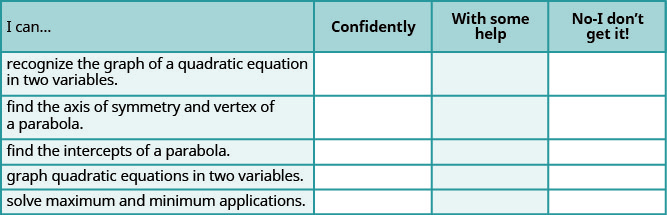
b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


