1.5: Ecuaciones cuadráticas con Raíces Complejas

En la Sección\(1.3,\) se consideró la solución de ecuaciones cuadráticas que tenían dos raíces de valor real. Esto se debió a que al calcular las raíces para cada ecuación, la porción de la fórmula cuadrática que es de raíz cuadrada (\(b^{2}-4 a c,\)a menudo llamada discriminante) siempre fue un número positivo.

Por ejemplo, al usar la fórmula cuadrática para calcular las raíces de la ecuación\(x^{2}-6 x+3=0,\) el discriminante es positivo y terminaremos con dos raíces de valor real:
\ [
\ begin {array} {c}
x^ {2} -6 x+3=0\\
a=1, b=-6, c=3\\
=\ frac {- ( -6)\ pm\ sqrt {(-6) ^ {2} -4 (1) (3)}} {2 * 1}\\
=\ frac {6\ pm\ sqrt {36-12}} {2}\\
=\ frac {6\ pm\ sqrt {24}} {2}\\
=\ frac {6\ pm 4.899} {2}
\ end {array}

\] start {array} {ll}
\ approx\ frac {6+4.899} {2} &\ approx\ frac {6-4.899} {2}\\
\ aprox\ frac {10.899} {2} &\ approx\ frac {1.101} {2}\\
\ aprox 5.449 &\ aproximadamente 0.551
\ fin {array}

Cuando agregamos y restamos la raíz cuadrada de 24 a 6 en la fórmula cuadrática, esto creó dos respuestas, y fueron de valor real porque la raíz cuadrada de 24 es de valor real.

Otra forma de ver esto es gráficamente. Si graficamos\(y=x^{2}-6 x+3\) y encontramos los\(x\) valores que\(y=0,\) los hacen aparecerán a lo largo del\(x\) eje -axis, y serán los mismos valores que resuelven la ecuación\(x^{2}-6 x+3=0\)

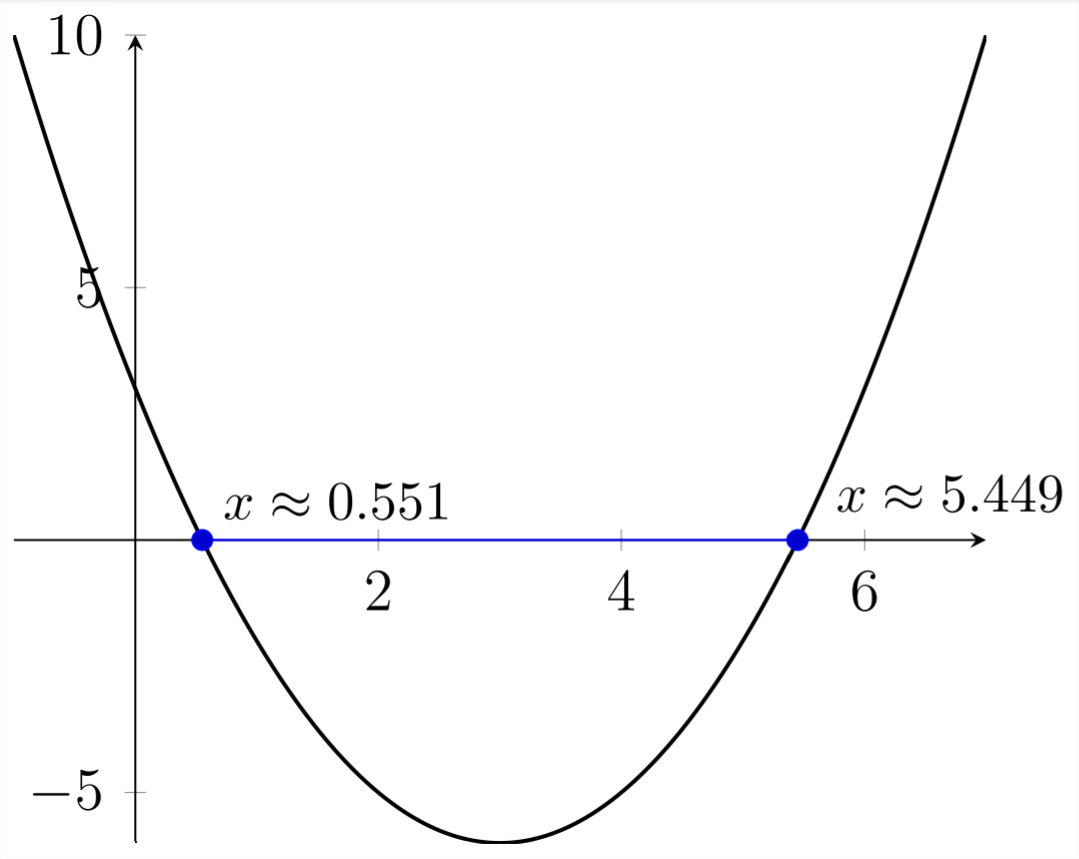
Si consideramos una ecuación relacionada, pero ligeramente diferente para empezar, estas relaciones entre las raíces, la discriminante y las intersecciones gráficas serán ligeramente diferentes.
\ [
\ begin {array} {c}
x^ {2} -6 x+9=0\\
a=1, b=-6, c=9
\ end {array}
\]

\ begin {alineado}
x &=\ frac {- (-6)\ pm\ sqrt {(-6) ^ {2} -4 (1) (9)}} {2 * 1}\\
&=\ frac {6\ pm\ sqrt {36-36}} {2}\\
&=\ frac {6\ pm\ sqrt {0}} {2}\\
&=\ frac 6} {2} =3
\ final {alineado}

Debido a que el discriminante era 0 en este problema, solo obtenemos una respuesta de valor real.

Gráficamente, los 6 adicionales que se agregaron a la ecuación original para cambiarla de\(x^{2}-6 x+3\) a\(x^{2}-6 x+9\) desplaza cada\(y\) valor en la gráfica hasta 6 unidades.

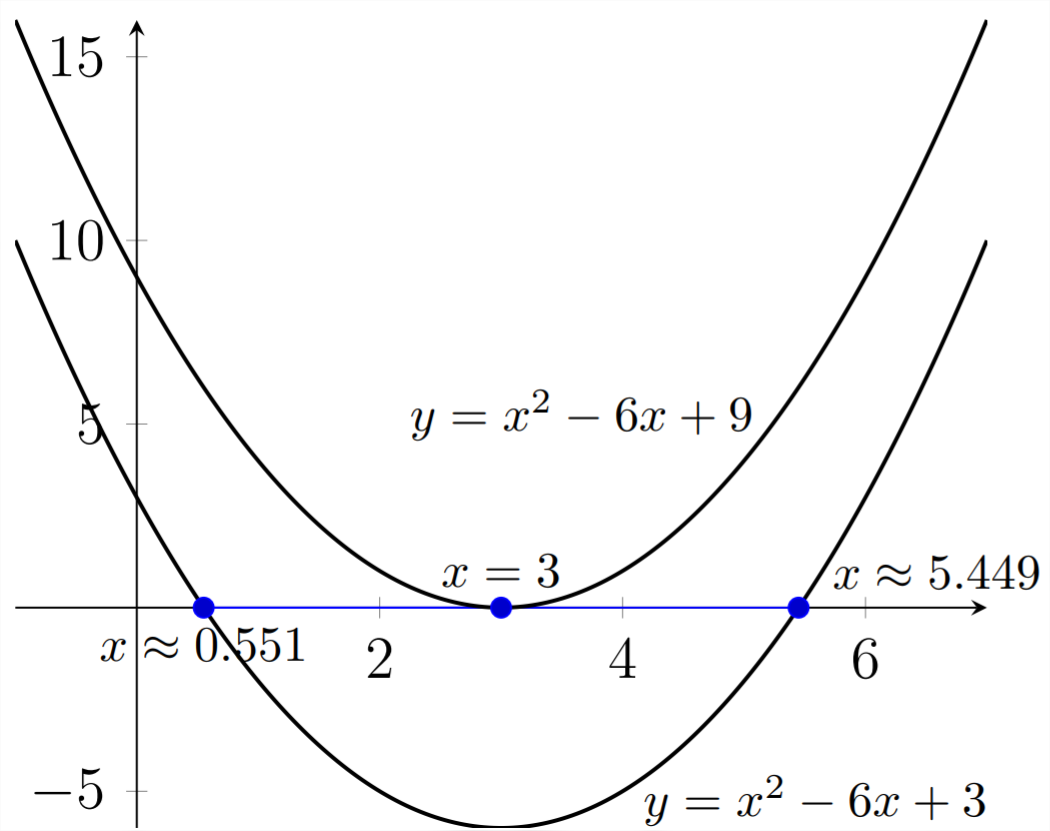
Si agregamos tres unidades adicionales al término constante de esta ecuación cuadrática, nos encontramos con una tercera posibilidad.

\ begin {array} {c}
x^ {2} -6 x+12=0\\
a=1, b=-6, c=12\\
=\ frac {- (-6)\ pm\ sqrt {(-6) ^ {2} -4 (1) (12)}} {2 * 1}\\
=\ frac {6\ pm\ sqrt {36-48}} {2}\\
= frac {6\ pm\ sqrt {-12}} {2}\\
=\ frac {6} {2}\ pm\ frac {6\ cdot 464 i} {2}\\
\ approx 3\ pm 1.732 i
\ end {array}

Aquí el discriminante es negativo, lo que lleva a dos respuestas de valor complejo. Si la ecuación tiene coeficientes de valor real, las raíces complejas siempre vendrán en pares conjugados. Los conjugados complejos comparten la misma parte de valor real y tienen signos opuestos en sus partes de valor complejo (o imaginario):\(a \pm b i\)

Gráficamente, el problema anterior estaba a un paso de no intersectar el\(x\) eje en absoluto y las tres unidades adicionales que agregamos para obtener\(y=x^{2}-\)\(6 x+12\) mueven la gráfica completamente lejos del\(x\) eje -eje. Debido a que las raíces son de valor complejo, no vemos ninguna raíz en el\(x\) eje. El\(x\) eje -contiene solo números reales.

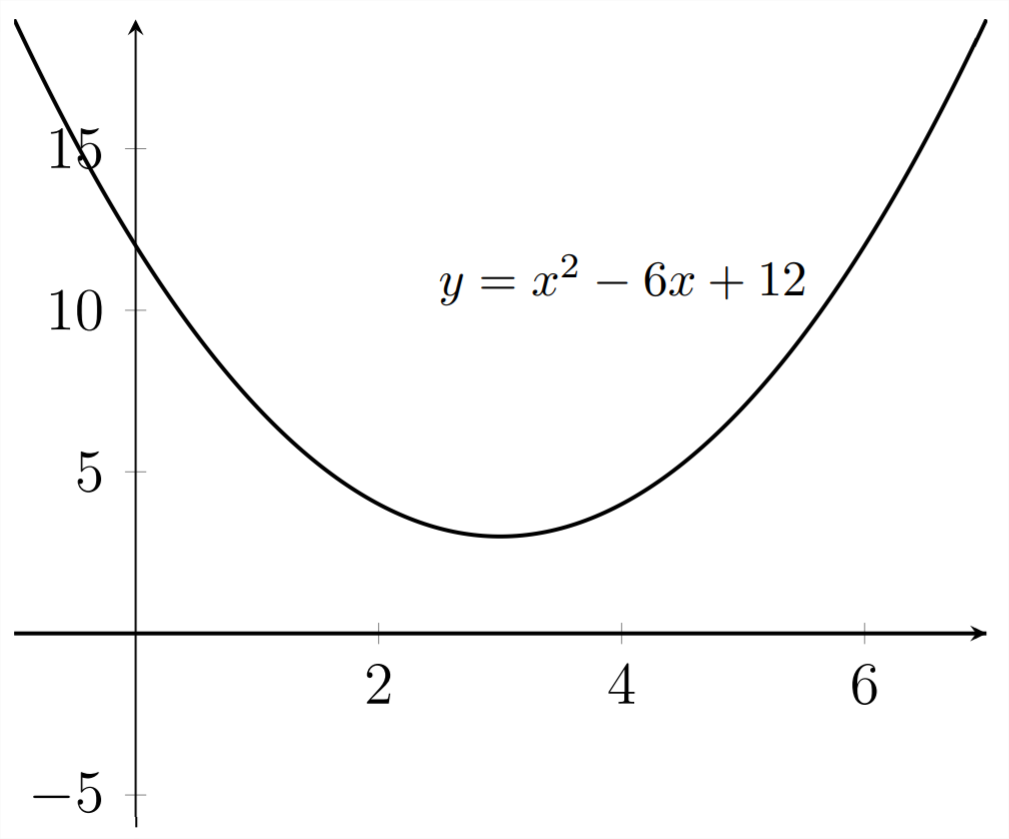
ya que la calculadora ha sido programada para la fórmula cuadrática, el foco de los problemas en esta sección será ponerlos en forma estándar.

Ejemplo\(\PageIndex{1}\)

Resolver para\(x\)
\((2 x+1)(x+5)-2 x(x+7)=5(x+3)^{2}\)

Solución

\ [
\ begin {array} {c}
(2 x+1) (x+5) -2 x (x+7) =5 (x+3) ^ {2}\\
2 x^ {2} +11 x+5-2 x^ {2} -14 x=5 (x+3) (x+3)\\ -3 x+5=5\ izquierda (x^ {2} +6 x+9\ derecha)\\
-3 x+5=5\ izquierda (x^ {2} +6 x+9\ derecha)\\
-3 x+5 = izquierda (x^ {+5=5 x^ {2} +30 x+45\\
0=5 x^ {2} +33
x+40\ x=5, b=33, c=40\\
x=-5, -1.6
\ end {array}
\]

El hecho de que las raíces de esta ecuación fueran números racionales significa que la ecuación podría haberse resuelto factorizando.
\ [
\ begin {array} {cc}
0=5 x^ {2} +33 x+40\\
0 =( 5 x+8) (x+5)\\
5 x=-8 & x+5=0\\
5 x+8=0 & x=-5\
x=-1.6 &
\ end {array}
\]

Ejemplo\(\PageIndex{1}\)

Resolver para\(x\)
\((x-2)^{2}+3(4 x-1)(x+1) &=7(x+1)(x-1)\)

Solución

\ [
\ begin {alineado}
x^ {2} -4 x+4+3\ izquierda (4 x^ {2} +3 x-1\ derecha) &=7\ izquierda (x^ {2} -1\ derecha)\\
x^ {2} -4 x+4+12 x^ {2} +9 x-3 &=7 x^ {2} -7\
13 x^ {2} +5 x+1 &=7 x^ {2} -7\\
6 x^ {2} +5 x+8 &=0\\
a=6, b=5, c=8 &\\
x\ aprox-0.41\ overline {6}\ pm 1.077 i\ approx-\ frac {5} {12}\ pm 1.077 i
\ end {alineado}
\]

Ejercicio\(\PageIndex{1}\)

Resuelve para\(x\) en cada ecuación. Redondear cualquier valor irracional a las 1000 th más cercanas.
1)\(\quad 3 x^{2}-3 x=4\)
2)\(\quad 4 x^{2}-2 x=7\)
3)\(\quad 5 x^{2}=3-7 x\)
4)\(\quad 3 x^{2}=21-14 x\)
5)\(\quad 6 x^{2}+1=2 x\)
6)\(\quad 5 x-3 x^{2}=17\)
7)\(\quad (5 x-1)(2 x+3)=3 x-20\)
8)\(\quad (x+4)(3 x-1)=9 x-5\)
9)\(\quad (x-2)^{2}=8 x(x-1)+10\)
10)\(\quad (2 x-3)^{2}=2 x-7 x^{2}\)
11)\(\quad (x+5)(x-6)=(2 x-1)(x-4)\)
12)\(\quad (3 x-4)(x+2)=(2 x-5)(x+5)\)

Contestar

1)\(\quad x \approx 1.758,-0.758\)
3)\(\quad x \approx 0.344,-1.744\)
5)\(\quad x \approx 0.1 \overline{6} \pm 0.373 i\)
7)\(\quad x \approx-0.5 \pm 1.204 i\)
9)\(\quad x \approx 0.286 \pm 0.881 i\)
11)\(\quad x \approx 4 \pm 4.243 i\)