1.4: Números Complejos

Nuestro sistema de números se puede subdividir de muchas maneras diferentes. La forma más básica de las matemáticas es contar y casi todas las culturas humanas tienen palabras para representar números (el Pirahã de Sudamérica son una notable excepción). Así, el conjunto de números más básico es el conjunto de números de conteo representado por la doble barra\(\mathrm{N}: \mathbb{N}=\{1,2,3,4,5,6,7, \ldots\}\) (dejaremos de lado el debate sobre si se debe incluir o no cero en este conjunto).

Si tratamos de restar un número de conteo mayor de un número de conteo menor nos encontramos con que no hay miembros en el conjunto de números de conteo para representar la respuesta en esta situación. Esto extiende el conjunto de números naturales al conjunto de enteros:\(\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\} .\) Los enteros son represnetados por el doble barrado\(Z\), para la palabra alemana para números-"zahlen”. En las primeras apariciones de números negativos en los sistemas matemáticos chino e indio, los valores negativos se utilizaron a menudo para representar la deuda. Debido a que las matemáticas griegas se basaban en la Geometría, no utilizaron números negativos.

Pasando a la multiplicación y división, si cuestionamos el valor de\(8 \div 2=4\) versus\(8 \div 3=?,\), una vez más debemos ampliar nuestra concepción de números para permitir una respuesta a la segunda pregunta\(8 \div 3=?\). Comprender las proporciones de números enteros o números racionales permite soluciones a tales problemas. El conjunto de números racionales está representado por el doble barrado\(Q\), para representar un cociente:
\(\mathbb{Q}=\left\{\frac{a}{b}: a, b \in \mathbb{Z}\right\}\)

La comprensión griega de los números en su mayoría se detuvo aquí. Consideraban que todas las cantidades podían representarse como la proporción de números enteros. La longitud de la diagonal de un cuadrado cuyos lados son de longitud 1 produjo una consternación considerable entre los pitagóricos como resultado de esto. Usando el Teorema de Pitágoras para la diagonal de un cuadrado cuyos lados son de longitud 1 muestra que la diagonal sería\(c^{2}=1^{2}+1^{2}=2,\) así\(c=\sqrt{2} .\) Este número no puede ser representado como una relación de números enteros. Esta nueva clase de números suma el conjunto
de números irracionales al conjunto existente de números racionales para crear los números reales, representados con un doble barrado\(\mathrm{R}\):\(\mathbb{R}\).

Esta jerarquía de números a menudo se representa en el siguiente diagrama:

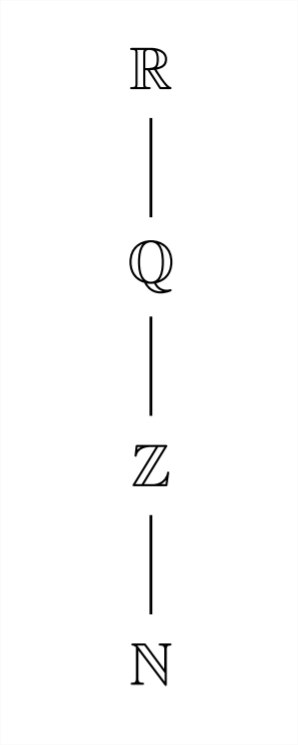
Una de las mejores formas de conceptualizar el sistema de números reales es en la línea numérica: cada punto de la línea numérica corresponde a un número real único y cada número real corresponde a una posición única en la línea numérica real.

Después del desarrollo de la imprenta en el siglo XV, Liber Abaci de Fibonacci se tradujo al italiano del latín y se leyó en toda Italia. Como resultado, Italia se convirtió en un próspero centro de matemáticas hasta el siglo XVII, cuando el centro de las matemáticas europeas se trasladó al norte a Francia, Alemania e Inglaterra.

A lo largo de la década de 1500 matemáticos italianos como Girolamo Cardano, Raphael Bombelli y Niccolo Fontana Tartaglia trabajaron para extender las ideas en el libro de Fibonacci. Produjeron fórmulas para resolver ecuaciones de grado cúbico (\(x^{3}\)) y cuártico (\(x^{4}\)). Al resolver algunas de estas ecuaciones encontraron que sus fórmulas a veces producían valores negativos bajo una raíz cuadrada. Ninguno de los sistemas numéricos conocidos podría acomodar esta posibilidad. En el libro de Cardano sobre álgebra Ars Magna, se encuentra con un problema que involucra la raíz cuadrada de un número negativo. Dice: “Está claro que este caso es imposible. Sin embargo vamos a trabajar así...” y procede a computar una solución compleja válida al problema. Los matemáticos finalmente definieron la unidad compleja\(\sqrt{-1}=i\) y luego

ideó un sistema en el que todos los números complejos son una combinación de una parte Real
\((a)\) y una parte “imaginaria” (bi).
Los números complejos son un sistema numérico bidimensional representado por el doble barrado\(C: \mathbb{C}=\{a+b i: a, b \in \mathbb{R}\},\) donde\(i\) se define la unidad compleja como\(i=\sqrt{-1} .\) A lo largo de finales de 1700 y principios del 1800 los matemáticos avanzaron gradualmente hacia una interpretación geométrica de la bidimensional números complejos. Lo que hoy se conoce como el “diagrama de Argand” representa la porción valorada real de un número complejo a lo largo de un eje horizontal y el múltiplo de la unidad compleja a lo largo del eje vertical.

Expresando raíces cuadradas de números negativos

Las raíces cuadradas de cantidades negativas generalmente se expresan como un múltiplo de\(i\)

Ejemplo\(\PageIndex{1}\)

\ [
\ begin {array} {c}
\ sqrt {-4} =2 i\\
\ sqrt {-25} =5 i\\
\ sqrt {-7}\ aproximadamente 2.646 i
\ end {array}
\]

Sumar, restar y multiplicar con números complejos

El cálculo con números complejos tiene muchas similitudes con el trabajo con variables. La parte real y la parte imginaria se tratan por separado para sumar y restar, pero pueden multiplicarse y dividirse.

Ejemplo\(\PageIndex{2}\)

Calcular lo siguiente:

\ [
\ begin {array} {c}
(6-4 i) + (-2+7 i) =4+3 i\\
(-9+2 i) - (-4+6 i) =-9+2 i+4-6 i=-5-4 i\\
3 (10+i) =30+3 i\\
-7 i (-5+8 i) =35 i-56 i^ {2}
\ end {array}
\]

Ahora nos encontramos con un dato interesante sobre los números complejos y, en particular, la unidad compleja Por definición,\(i .\) por\(i=\sqrt{-1} .\) lo tanto, si\(i\) nos cuadramos deberíamos obtener\(-1 .\) En el último ejemplo problema anterior, podemos\(i^{2}\) sustituir el por -1 para terminar el problema.

\ begin {alineado}
-7 i (-5+8 i) &=35 i-56 i^ {2}\\
&=35 i-56 (-1)\\
&=35 i+56\\
&=56+35 i
\ end {alineado}

Ejemplo\(\PageIndex{3}\)

Calcular lo siguiente:

\ [
\ begin {alineado}
(8-5 i) (1-4 i) &=8-32 i-5 i+20 i^ {2}\\
&=8-37 i+20 (-1)\\
&=8-37 i-20\\
&=-12-37 i\\
\
(9+2 i) ^ {2} & =( 9+2 i) (9+2 i) (9+2 i)\\
i=81+18 i+18 +4 i^ {2}\\
&=81+36 i+4 (-1)\\
&=81+36 i-4\\
&=77+36 i
\ end {alineado}
\]

Poderes de\(i\)

Los poderes de\(i\) seguir un patrón interesante basado en la definición de que\(i^{2}=-1\)
Podemos ver eso\(i^{1}=i\) y que\(i^{2}=-1,\) como resultado, de una\(i^{3}=i^{2} * i^{1}=-1 * i=-i\)
manera similar,\(i^{4}=i^{2} * i^{2}=(-1)(-1)=1\)
Esto quiere decir que\(i^{5}=i^{4} * i=1 * i=i\)
si ponemos todos esta información en conjunto obtenemos lo siguiente:
\(i^{1}=i\)
\(i^{2}=-1\)
\(i^{3}=-i\)
\(i^{4}=1\)
\(i^{5}=i^{1}=i\)
\(i^{6}=i^{2}=-1\)
\(i^{7}=i^{3}=-i\)
\(i^{8}=i^{4}=1\)
En otras palabras, cada poder de\(i\) es equivalente a cualquiera\(i,-1,-i,\) o\(1 .\) Para determinar a cuál de estos valores\(i\) es equivalente una potencia, necesitamos encontrar el resto del exponente cuando se divide por 4

Ejemplo\(\PageIndex{4}\)

Simplificar\(i^{38}\)

Solución

ya que cada\(i^{4}=1,\) entonces\(i^{38}=i^{36} * i^{2}=\left(i^{4}\right)^{9} * i^{2}=1^{9} * i^{2}=i^{2}=-1\)
desde 38 es 2 más que un múltiplo de\(4,\) entonces\(i^{38}=i^{2}=-1\)

Ejercicio\(\PageIndex{1}\)

Grafique los siguientes números complejos:

1)\(\quad 2+5 i\)
2)\(\quad 4-3 i\)
3)\(\quad -2+6 i\)
4)\(\quad -3-5 i\)
5)\(\quad 4\)
6)\(\quad -2 i\)
7)\(\quad 7-i\)
8)\(\quad -1+i\)
9)\(\quad -8+4 i\)
10)\(\quad 8+3 i\)
11) \(\quad 7 i\)
12)\(\quad -5-9 i\)

Exprese cada cantidad en términos de valores irracionales\(i .\) redondos al 1000 th más cercano.
13)\(\quad \sqrt{-36}\)
14)\(\quad \sqrt{-81}\)
15)\(\quad \sqrt{-100}\)
16)\(\quad \sqrt{-49}\)
17)\(\quad \sqrt{-4}\)
18)\(\quad \sqrt{-25}\)
19)\(\quad \sqrt{-2}\)
20)\(\quad \sqrt{-6}\)
21)\(\quad \sqrt{-10}\)
22) \(\quad \sqrt{-31}\)
23)\(\quad \sqrt{-5}\)
24)\(\quad \sqrt{-3}\)

Realizar la operación indicada y simplificar
25)\(\quad(6+7 i)+(5+3 i)\)
26)\(\quad(4-5 i)+(3+9 i)\)
27)\(\quad(9+8 i)-(1-2 i)\)
28)\(\quad(2+i)-(6-4 i)\)
29)\(\quad(7-4 i)-(5-3 i)\)
30)\(\quad(8+i)-(4+3 i)\)
31)\(\quad(7 i)(6 i)\)
32)\(\quad(4 i)(-8 i)\)
33)\(\quad(-2 i)(5 i)\)
34)\(\quad(12 i)(3 i)\)
35)\(\quad(1+i)(3+2 i)\)
36)\(\quad(1+5 i)(4+3 i)\)
37)\(\quad(6-5 i)(2-3 i)\)
38)\(\quad(8-3 i)(2+i)\)
39)\(\quad(-3+4 i)(-1-2 i)\)
40)\(\quad(-7-i)(3-5 i)\)
41)\(\quad(4-2 i)^{2}\)
42) \(\quad(-5+i)^{2}\)
43)\(\quad(3+i)(3-i)\)
44)\(\quad(2+6 i)(2-6 i)\)
45)\(\quad(9-4 i)(9+4 i)\)
46)\(\quad(5+2 i)(5-2 i)\)

Expresar como cualquiera\(i,-1,-i,\) o 1
47)\(\quad i^{3}\)
48)\(\quad i^{7}\)
49)\(\quad i^{21}\)
50)\(\quad i^{13}\)
51)\(\quad i^{29}\)
52)\(\quad i^{56}\)
53)\(\quad i^{72}\)
54)\(\quad i^{35}\)
55) \(\quad i^{66}\)
56)\(\quad i^{103}\)
57)\(\quad i^{16}\)
58)\(\quad i^{53}\)
59)\(\quad i^{11}\)
60)\(\quad i^{42}\)
61)\(\quad i^{70}\)
62)\(\quad i^{9}\)

Contestar

13)\(\quad 6 i\)
15)\(\quad 10 i\)
17)\(\quad 2 i\)
19)\(\quad 1.414 i\)
21)\(\quad 3.162 i\)
23)\(\quad 2.236 i\)
25)\(\quad 11+10 i\)
27)\(\quad 8+10 i\)
29)\(\quad 2-i\)
31)\(\quad-42\)
33)\(\quad 10\)
35)\(\quad 1+5 i\)
37)\(\quad-3-28 i\)
39)\(\quad 11+2 i\)
41)\(\quad 12-16 i\)
43)\(\quad 10\)
45) \(\quad 97\)
47)\(\quad -i\)
49)\(\quad i\)
51)\(\quad i\)
53)\(\quad 1\)
55)\(\quad -1\)
57)\(\quad 1\)
59)\(\quad -i\)
61)\(\quad -1\)